AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 4th Lesson Pair of Linear Equations in Two Variables Optional Exercise
10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables Optional Exercise Textbook Questions and Answers
Question 1.
i) \(\frac{2x}{a}\) + \(\frac{y}{b}\) = 2
\(\frac{x}{a}\) – \(\frac{y}{b}\) = 4
Answer:

Substituting x = 2a in the equation (1) we get
\(\frac{2}{a}\)(2a) + \(\frac{y}{b}\) = 2
⇒ 4 + \(\frac{y}{b}\) = 2
⇒ \(\frac{y}{b}\) = -2
⇒ y = -2b
∴ The solution (x, y) = (2a, -2b)
![]()
ii) \(\frac{x+1}{2}\) + \(\frac{y-1}{3}\) = 8
\(\frac{x-1}{3}\) + \(\frac{y+1}{2}\) = 9
Answer:
Given: \(\frac{x+1}{2}\) + \(\frac{y-1}{3}\) = 8
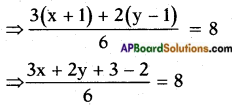
⇒ 3x + 2y + 1 = 48
⇒ 3x + 2y = 47 …… (1)
and \(\frac{x-1}{3}\) + \(\frac{y+1}{2}\) = 9
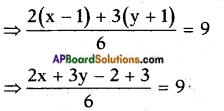
⇒ 2x + 3y + 1 = 54
⇒ 2x + 3y = 53 …… (2)
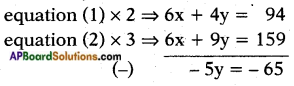
⇒ y = \(\frac{-65}{-5}\) = 13
Substituting y = 13 in equation (1) we get
3x + 2(13) = 47
⇒ 3x = 47 – 26
⇒ 3x = 21
⇒ x = \(\frac{21}{3}\) = 7
∴ The solution (x, y) = (7, 13)
iii) \(\frac{x}{7}\) + \(\frac{y}{3}\) = 5
\(\frac{x}{2}\) – \(\frac{y}{9}\) = 6
Answer:
Given: \(\frac{x}{7}\) + \(\frac{y}{3}\) = 5 and \(\frac{x}{2}\) – \(\frac{y}{9}\) = 6
⇒ \(\frac{3x+7y}{21}\) = 5 and \(\frac{9x-2y}{18}\) = 6
⇒ 3x + 7y = 105 …….. (1) and
9x – 2y = 108 …….. (2)
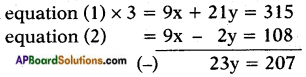
⇒ y = \(\frac{207}{23}\) = 9
Substituting y = 9 in equation (1) we get
3x + 7(9) = 105
⇒ 3x = 105 – 63
⇒ 3x = 42
⇒ x = \(\frac{42}{3}\) = 14
∴ The solution (x, y) = (14, 9)
![]()
iv) √3x + √2y = √3
√5x + √3y= √3
Answer:
Given that √3x + √2y = √3 …… (1)
√5x + √3y = √3 …… (2)
By following elimination method

Now again following elimination method

∴ The solution x = \(\frac{3-\sqrt{6}}{3-\sqrt{10}}\) and y = \(\frac{3-\sqrt{15}}{3-\sqrt{10}}\)
v) \(\frac{ax}{b}\) + \(\frac{by}{a}\) = a + b
ax – by = 2ab
Answer:
Given: \(\frac{ax}{b}\) + \(\frac{by}{a}\) = a + b ……. (1)
ax – by = 2ab …….. (2)

Substituting y = – a in equation (2)
we get ax – b(-a) = 2ab
ax + ab = 2ab
ax = 2ab – ab = ab
⇒ x = \(\frac{ab}{a}\) = b
∴ (x, y) = (b, -a)
![]()
vi) 2x + 3y = 17
2x+2 – 3y+1 = 5
Answer:
Given: 2x + 3y = 17 and
2x+2 – 3y+1 = 5
Take 2x = a and 3y = b then the given equations reduce to
2x + 3y = 17 ⇒ a + b = 17 …… (1)
2x . 22 – 3y . 3 = 5 ⇒ 4a – 3b = 5 …… (2)

Substituting b = 9 in equation (1) we get
a + 9 = 17 ⇒ a = 17 – 9 = 8
But a = 2x – 8 and b = 3y = 9
⇒ 2x = 23 and 3y = 32
⇒ x = 3 and y = 2
∴ The solution (x, y) is (3, 2)
![]()
Question 2.
Animals in an experiment are to be kept on a strict diet. Each animal is to receive among other things 20g of protein and 6g of fat. The laboratory technicians purchased two food mixes, A and B. Mix A has 10% protein and 6% fat. Mix B has 20% protein and 2% fat. How many grams of each mix should be used?
Answer:
Let x gms of mix A and y gms of mix B are to be mixed, then

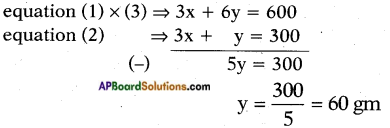
Substituting y = 60 in equation (1)
we get x + 2 × 60 = 200
⇒ x + 120 = 200
⇒ x = 200 – 120 = 80 gm
∴ Quantity of mix. A = 80 gms.
Quantity of mix. B = 60 gms.