AP State Syllabus AP Board 9th Class Physical Science Important Questions Chapter 8 Gravitation
AP State Syllabus 9th Class Physical Science Important Questions 8th Lesson Gravitation
9th Class Physical Science 8th Lesson Gravitation 1 Mark Important Questions and Answers
Question 1.
Write the precautions to be taken while doing an activity to locate centre of gravity of a regular object?
Answer:
- Tie the rope at geometrical centre of an regular object.
- Draw the line along the rope after object come to rest.
Question 2.
What path will moon take when the moon stops rotating round the earth?
Answer:
Moon take the path of tangent to the orbit, in which it rotates around the earth.
9th Class Physical Science 8th Lesson Gravitation 2 Marks Important Questions and Answers
Question 1.
If a person of mass 60 kg went to the Moon, then
a) Is there any change in his Mass and Weight?
Answer:
Mass does not change and remains 60 kgs. But, weight changes,
b) What will be his weight on the Earth?
Answer:
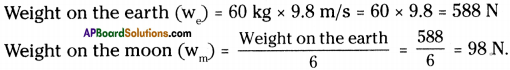
Question 2.
Consider the gravitational force formula \(\mathbf{F}=\mathbf{G} \frac{\mathbf{M}_{1} \mathbf{M}_{2}}{\mathbf{R}^{2}}\) and answer the following
questions.
i) What is the value of G?
Answer:
G = 6.67 × 10-11 Nm² kg-2
ii) What does the term ‘R’ indicate here?
Answer:
R indicates “distance between two objects.”
![]()
Question 3.
To know about the center of gravity of the atmosphere of the earth, Ravi asked some questions to his teacher. Guess which question he asked and the answer given by the teacher.
Answer:
- Where would be the centre of gravity of atmosphere of earth?
- What is centre of gravity?
Answer from the teacher :
- The centre of gravity of the earth’s atmosphere is in the centre of the earth.
- The point where total weight appears to act is called centre of gravity.
Question 4.
Consider the following equation of motion and rewrite them for a free fall body v = u + at
s = ut + ½ at²
Answer:
For a free fall body u = 0; a = g and s
i) v = u + at ⇒ v = 0 + gt ⇒ v = gt
ii) s = ut + ½at² ⇒ h = 0 + ½gt² ⇒ h = ½gt²
9th Class Physical Science 8th Lesson Gravitation 4 Marks Important Questions and Answers
Question 1.
Two spherical balls of mass 20 kg each one placed with their centres 20 cm apart. Find the gravitational force of attraction between them.
(G = 6.67 × 10-11 Nm². Kg-2)
Answer:
Masses of balls M1 and M2 = 20 kg each
distance (d) = 20 cm = 0.2 m.
Gravitational force of attraction between M1 and M2
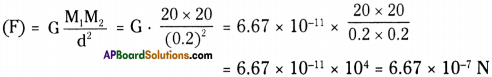
Question 2.
a) Draw the centre of gravity of the following uniform objects.
i) equilateral triangle
ii) square
iii) circle
Answer:
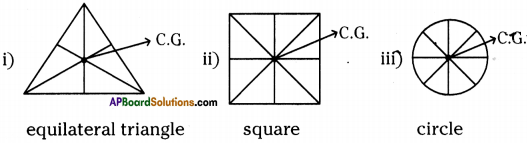
b) What is the speciality of centre of gravity of a material?
Answer:
- Stability depends upon the centre of gravity of a material.
- If we draw a line straight down from the centre of gravity of an object of any
shape and it falls inside the base of the object, then the object will be stable.
9th Class Physical Science 8th Lesson Gravitation Important Questions and Answers
9th Class Physical Science 8th Lesson Gravitation 1 Mark Important Questions and Answers
Question 1.
Define centripetal force.
Answer:
The net force which can change only the direction of the velocity of a body is called “centripetal force”.
Question 2.
Define centripetal acceleration.
Answer:
The acceleration which can change only the direction of velocity of a body is called “centripetal acceleration”.
![]()
Question 3.
State Newton’s universal law of Gravitation.
Answer:
The universal law of gravitation states that every body in the universe attracts other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Question 4.
What do you mean by acceleration due to gravity?
Answer:
The acceleration produced due to gravitational force of the earth near the surface is called free-fall acceleration or acceleration due to gravity.
Question 5.
What is universal gravitational constant?
Answer:
The value of ‘G’ i.e., the universal gravitational constant is equal to the magnitude of force between a pair of 1 kg – masses that are lm apart.
G = 6.67 × 10-11 Nm² kg-2.
Question 6.
When do you say that a body is freely falling?
Answer:
A body is said to be free-fall body when only one gravitational force acts on that body.
Question 7.
Define weight.
Answer:
Weight of a body is the force of attraction on the body due to earth.
W = mg
![]()
Question 8.
What is centre of gravity?
Answer:
The point where total weight appears to act is called centre of gravity.
Question 9.
When will a body be stable?
Answer:
If we draw a line straight down from the centre of gravity of an object of any shape and it falls inside the base of the object, then the object will be stable.
Question 10.
What is time period?
Answer:
The time taken by a body executing uniform circular motion, to complete one revolution is called time period.
Question 11.
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Answer:
Moon attracts with same gravitational forces as earth attracts moon. They form action reaction pair.
9th Class Physical Science 8th Lesson Gravitation 2 Marks Important Questions and Answers
Question 1.
Draw a diagram showing the balancing of fork and spoon.
Answer:
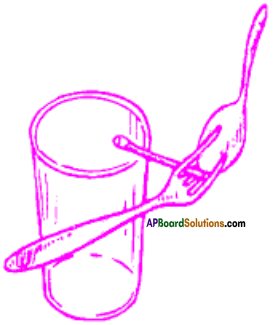
Question 2.
When could we say that an object is stable?
Answer:
If we draw a line straight down from the centre of gravity of an object of any shape and it falls inside the base of the object, then the object will stable.
If the line through the centre of gravity falls outside the base then the object will be unstable.
![]()
Question 3.
The mass of the earth is 6 × 1024 kg and that of the moon is 7.4 × 1022 kg. If the distance between the earth and the moon is 3.84 × 105 km. Calculate the force exerted by the earth on the moon.
Answer:
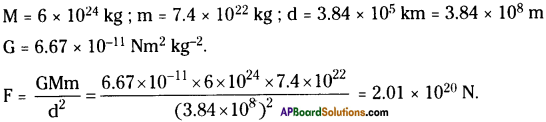
Thus the force exerted by the earth on the moon is 2.01 × 1020 N.
Question 4.
A car falls off an edge and drops to the ground in 0.5 s.
i) What is its speed on striking the ground?
ii) What is the average speed during the 0.5 s?
iii) What is the height of the edge from the ground?
Answer:

Question 5.
An object is thrown vertically upwards and rises to a height of 10 m. Calculate,
i) the velocity with which the object was thrown upwards.
ii) the time taken by the object to reach the highest point.
Answer:
i) s = 10 m, v = 0 m/s, a = – g = – 9.8 m/s2.
v² – u² = 2as
0 – u² = 2 × – 9.8 × 10 ⇒ u = \(\sqrt{196}\) ⇒ u = 14 m/s.
ii) v = u + at
0 = 14 – 9.8 × t
t = 1.43 s
Question 6.
Mass of an object is 10 kg. What is its weight on the earth?
Answer:
m = 10 kg, g = 9.8 m/s².
W = mg = 10 × 9.8 = 98 N.
![]()
Question 7.
Why is the weight of an object on moon 1/6th its weight on the earth?
Answer:
The acceleration due to gravity on moon is 1/6th of its value on earth.
We know, weight = mass × acceleration due to gravity.
∴ The weight on moon is 1 /6th its weight on earth.
Question 8.
How does the force of gravitation between two objects change when the distance between them is reduced to half?
Answer:
The force between two objects is inversely proportional to square of distance.
\(\mathrm{F} \propto \frac{1}{\mathrm{~d}^{2}}\)
If the distance between the objects reduced to half then force increases by four times.
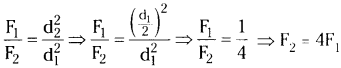
Question 9.
Gravitational force that acts on all objects is proportional to their masses. It is when a heavy object does not fall faster than a light object.
Answer:
The acceleration due to gravity attained by an object due to gravitational force does not depend on mass of the object. So heavy object and lighter object falls at a time on earth.
Question 10.
If the moon attracts the earth, why the earth does not move towards the moon?
Answer:
Moon attracts with same force as earth attracts moon. But we know acceleration is inversely proportional to mass. As the mass of earth is greater than moon. So earth does not move towards the moon.
Question 11.
What happens to force between two objects, if
i) the mass of one object is doubled?
ii) the distance between objects boubled and tripled?
iii) the masses of both objects are doubled?
Answer:
i) If mass of one object is doubled the force also would be doubled. Since F ∝ m.
ii) If the distance between the objects boubled and tripled the force is reduced by 4 times and 9 times respectively.
Scince, \(\mathrm{F} \propto \frac{1}{\mathrm{~d}^{2}}\)
iii) If masses of both the objects are doubled, then force is increased by 4 times.
Scince, F ∝ m1m2.
![]()
Question 12.
A ball is thrown vertically upward with a velocity of 49 m/s. Calculate,
i) the maximum height to which it rises.
ii) the total time to return to the surface of the earth.
Answer:
i) u = 49 m/s, g = 9.8 m/s².
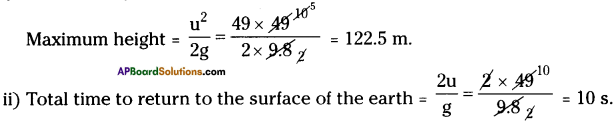
Question 13.
A stone is released from the top of tower of height 19.6 m. Calculate the final velocity just before touching the ground.
Answer:
h = 19.6
u = 0
a = + g = 9.8 m/s²
v² = 2gh
![]()
Question 14.
What is universal gravitational constant?
Answer:
The value of ‘G’ i.e., the universal gravitational constant is equal to the magnitude of force between a pair of 1 kg – masses that are lm apart.
G = 6.67 × 10-11 Nm² kg-2.
Question 15.
When does an object get stability?
(OR)
Write a short notes on “stability”.
Answer:
- The location of the center of gravity is important for stability.
- If we draw a line straight down from the center of gravity of an object of any shape and it falls inside the base of the object, then the object will be stable.
- If the line through the center of gravity falls outside the base, then the object will be unstable.
![]()
Question 16.
State the universal law of gravitation and explain it.
Answer:
The universal law of gravitation :
The universal law of’gravitation states that every body in the universe attracts other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
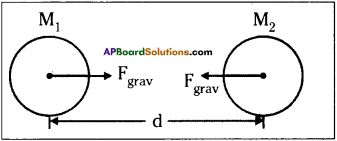
Explanation :
Let two bodies of masses M1 and M2 be separated by a distance of ’d’. Then the force of gravitation between them
![]()
G is a proportionality constant, called universal gravitational constant.
The value of G = 6.67 × 10-11 Nm² kg-2
9th Class Physical Science 8th Lesson Gravitation 4 Marks Important Questions and Answers
Question 1.
Define centripetal force and derive an expression for it.
Answer:
Centripetal force :
The net force which can change only the direction of the velocity of a body is called “centripetal force.”
Derivation :
Newton’s second law says that the net force on a moving body produces an acceleration in it, which is directed along the net force.
So in uniform circular motion, a net force acts towards the centre, called as centripetal force.
According to Newton’s second law of motion,

Here R is the radius of the circle.
Question 2.
Calculate the speed of moon.
Answer:
1) We know that the motion of the moon around the earth is approximately uniform circular motion.
2) We can calculate the speed of the moon using the equation.
\(\mathrm{v}=\frac{2 \pi \mathrm{R}}{\mathrm{T}}\) ……… (1)
R = distance of the moon from the centre of the earth
T = Time period of the moon
3) Thus the acceleration of the moon towards the centre of the earth
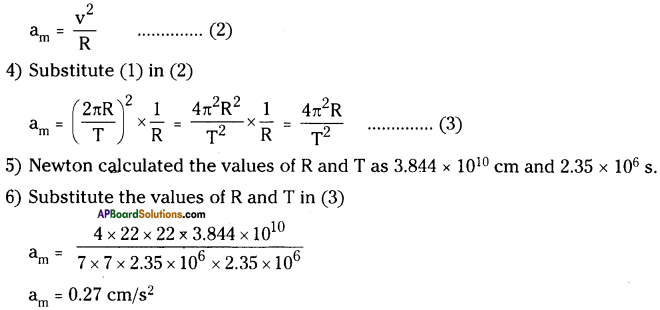
Question 3.
What is the ‘universal law of gravitation’? Derive a formula to it.
(OR)
Derive \(\mathbf{F}_{\text {grav }}=\frac{\mathbf{G M}_{1} \mathbf{M}_{2}}{\mathbf{d}^{2}}\)
Answer:
1) The universal law of gravitation states that every body in the universe attracts other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
2) The direction of the force of attraction is along the line joining the centers of the two bodies.
3) Let two bodies of masses M1 and M2 be separated by a distance of ’d’. Then the force of gravitation between them.
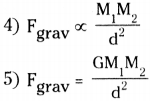
6) G is a proportionality constant called universal gravitational constant and found by Henry cavendish to be G = 6.67 × 10-11 Nm² Kg-2
![]()
Question 4.
Prove that acceleration due to gravity is independent of masses.
Answer:
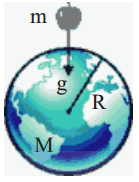
Let us drop a body of mass’m’ near the earth’s surface.
Let ‘M’ be the mass of the earth and ‘R’ be the radius of the earth.
Now the force of attraction on the mass is given by
\(\mathrm{F}=\frac{\mathrm{GMm}}{\mathrm{r}^{2}} \Rightarrow \frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
From Newton’s second law, F/m is equal to acceleration.
Here this acceleration is denoted by ’g’.
Hence, \(\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
From above equation, we can conclude that g’ is independent of the mass of the body.
Question 5.
Find the acceleration of a body which is in uniform circular motion with speed ‘v’ and radius ‘R’.
(OR)
Derive \(\mathrm{a}_{\mathrm{c}}=\frac{\mathrm{V}^{2}}{\mathrm{R}}\)
1) Let a body move with a constant speed ‘v’ in a circular path of radius ‘R’.
2) DV will be represented by the base of the isosceles triangle as shown in the figure.
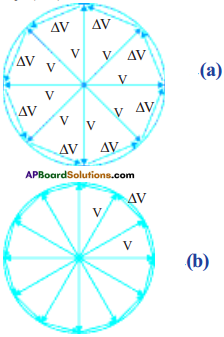
3) The exact value of the sum of the magnitudes of the changes in velocity of the body during the course of revolution will be equal to the circumference ‘2πu” of the circle.
4) We know that the magnitude of the acceleration is equal to the ratio of magnitude of change in velocity for one revolution and the time period.
5) Let ac be magnitude of acceleration of the body in uniform circular motion.
6) That is ac = 2π v/T.
7) Where ‘T’ is time required to complete one revolution.
8) We know that T = \(\frac{2 \pi \mathrm{R}}{\mathrm{v}}\)
9) Substituting this expression we get \(a_{c} \frac{v^{2}}{R}\)
![]()
Question 6.
How can you find the center of gravity of an irregular body?
Answer:
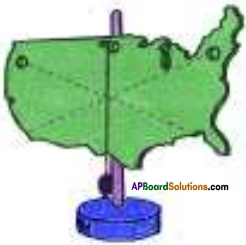
- Take an irregular shaped object.
- Suspend a plum in one position and draw a line along the rope of the plum.
- Change the position of the object and do the same.
- In this way draw lines in all possible positions.
- The center of gravity lies where the lines intersect.
- In this way we can find the center of gravity of an irregular shaped object.