AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు Ex 8.4 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు Exercise 8.4
ప్రశ్న 1.
ABC త్రిభుజంలో AB పై D ఒక బిందువు మరియు AD = \(\frac {1}{4}\) AB. ఇదే విధంగా AC పై బిందువు E మరియు AE = \(\frac {1}{4}\)AC, DE = 2 సెం.మీ. అయిన BC ఎంత?
సాధన.
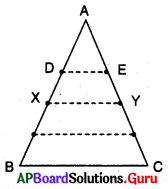
∆ABC లో D మరియు E లు AB మరియు AC లపై గల బిందువులు.
ఈ బిందువులు AD = \(\frac {1}{4}\) AB మరియు AE = \(\frac {1}{4}\) AC.
X, Yలు AB మరియు AC ల మధ్య బిందువులు అనుకొనుము.
D, E మరియు X, Y లను కలుపుము.
∆AXY, D, E E AX మరియు AY ల మధ్య బిందువులు.
∴ DE // XY మరియు DE = \(\frac {1}{2}\)XY
DE = 2 సెం.మీ. కావున
⇒ 2 = \(\frac {1}{2}\)XY
⇒ XY = 2 × 2 = 4 సెం.మీ.
అదే విధంగా ∆ABC లో X, Y లు AB మరియు AC ల మధ్య బిందువులు.
∴ XY // BC మరియు XY = \(\frac {1}{2}\)BC
XY = 4 సెం.మీ.
కావున BC = 4 × 2 = 8 సెం.మీ
![]()
ప్రశ్న 2.
ABCD చతుర్భుజములో AB, BC, CD మరియు DA ల మధ్య బిందువులు E, F, G మరియు H లు అయిన EFGH సమాంతర చతుర్భుజమని నిరూపించుము.
సాధన.
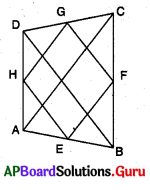
ABCD చతుర్భుజములో భుజాల యొక్క మధ్య బిందువులు E, F, G మరియు H లు.
∆ABC లో AB మరియు BC ల యొక్క మధ్య బిందువులు E మరియు F అనుకొనుము.
∴ EF // AC మరియు EF – – AC . అట్లాగే AACD లో HG // AC
మరియు HG = \(\frac {1}{2}\) AC
∴ EF // HG మరియు EF = HG
చతుర్భుజము EFGH లో EF = HG మరియు EF // HG.
∴ EFGH ఒక సమాంతర చతుర్భుజము.
ప్రశ్న 3.
రాంబస్ యొక్క భుజాల మధ్య బిందువులను వరుసగా కలిపితే ఏర్పడే పటం దీర్ఘచతురస్రమని చూపండి.
సాధన.
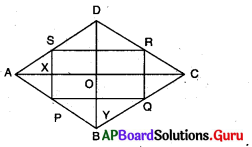
☐ABCD ఒక రాంబస్.
P, Q, R మరియు వీలు రాంబస్ ☐ABCD యొక్క భుజాల మధ్య బిందువులు,
∆ABC లో P, Qలు AB మరియు BCల యొక్క మధ్య బిందువులు.
∴ PQ // AC మరియు PQ = \(\frac {1}{2}\)AC ……… (1)
అదే విధంగా ∆ADC లో S, R లు AD మరియు CDల యొక్క మధ్య బిందువులు.
∴ SR // AC మరియు SR = \(\frac {1}{2}\)AC …….. (2)
(1) మరియు (2) ల నుండి
PQ // SR మరియు PQ = SR
అదే విధముగా QR // PS మరియు QR = PS
∴ ☐PQRS ఒక సమాంతర చతుర్భుజము.
రాంబన్ యొక్క కర్ణాలు లంబనమద్విఖండన చేసుకొనును కావున \(\angle \mathrm{AOB}\) = 90°
∴ \(\angle \mathrm{P}=\angle \mathrm{AOB}\) = 90°
[//gm PYOX యొక్క ఎదుటి కోణాలు]
∴ PQRS ఒక దీర్ఘచతురస్రము. ఎందుకనగా రెండు జతల ఎదుటి భుజాలు సమానము మరియు సమాంతరాలు, ఒక కోణము 90° కాబట్టి.
![]()
ప్రశ్న 4.
ABCD సమాంతర చతుర్భుజములో AB, DCE మధ్య బిందువులు వరుసగా E మరియు F అయిన AF మరియు EC రేఖాఖండాలు కర్ణము BD ని త్రిథాకరిస్తాయని చూపండి.
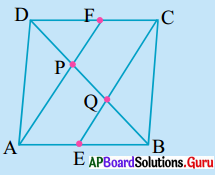
సాధన.
ABCD ఒక సమాంతర చతుర్భుజము. E మరియు Fలు AB మరియు CD భుజాల మధ్య బిందువులు.
∴ AE = \(\frac {1}{2}\)AB మరియు CF = \(\frac {1}{2}\)CD
అదే విధముగా AE = CF [∵ AB = CD]
చతుర్భుజము AECF లో AE = CF మరియు
AE // CF కావున AECF ఒక సమాంతర చతుర్భుజము.
∆EQB మరియు ∆FDP లలో
EB = FD [//gm యొక్క సగ భుజాలు సమానము]
\(\angle \mathrm{EBQ}=\angle \mathrm{FDP}\) [EB // FD కావున ఏకాంతర కోణాలు]
\(\angle \mathrm{QEB}=\angle \mathrm{PFD}\)
[∵ \(\angle \mathrm{QED}=\angle \mathrm{QCF}=\angle \mathrm{PFD}\)]
∴ ∆EQB ≅ ∆FPD (తో. భు. తో. నియమం)
∴ BQ = DP [∵ CPCT] ………. (1)
∆DQC లో; PF // QC మరియు F, DC భుజపు మధ్య బిందువు
DQ మధ్య బిందువు P కావున
DP PQ …………. (2)
(1) మరియు (2) ల నుండి, DP = PQ = QB.
∴ కర్ణము BD ని AF మరియు CE లు త్రిథాకరిస్తాయి.
ప్రశ్న 5.
చతుర్భుజములో ఎదుటి భుజాల మధ్య బిందువులను కలుపుతూ గీయబడిన రేఖాఖండాలు సమద్విఖండన చేసుకుంటాయని చూపండి.
సాధన.
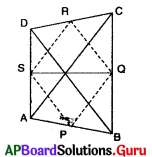
ABCD ఒక చతుర్భుజము అనుకొనుము.
P, Q, R, S లు చతుర్భుజము ABCD యొక్క భుజాల మధ్య బిందువులు.
(P, Q), (Q, R), (R, S) మరియు (S, P) లను కలుపుము.
∆ABC లో P, Qలు AB మరియు BC ల మధ్య బిందువులు.
∴ PQ // AC మరియు PQ = \(\frac {1}{2}\)AC ……… (1)
∆ADC నుండి, S, Rలు AD మరియు CDల మధ్య బిందువులు.
∴ SR // AC మరియు SR = \(\frac {1}{2}\)AC …….. (2)
∴ (1) మరియు (2) ల నుండి,
PQ = SR మరియు PQ // SR
∴ PQRS ఒక సమాంతర చతుర్భుజము.
PQRS సమాంతర చతుర్భుజములో PR మరియు QSలు కర్ణాలు.
∴ PR మరియు QS లు సమద్విఖండన చేసుకొనును.
![]()
ప్రశ్న 6.
ABC లంబకోణ త్రిభుజములో C లంబకోణం. కర్ణము ABమధ్యబిందువు M గుందా BCకు సమాంతరముగా గీచిన రేఖ AC ని D వద్ద ఖండిస్తే కింది వానిని నిరూపించండి.
(i) AC మధ్య బిందువు D
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\)AB
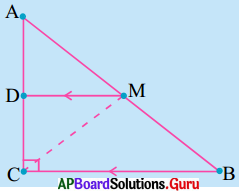
సాధన.
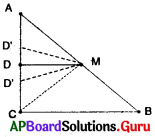
∆ABC లో \(\angle \mathrm{C}\) = 90° మరియు AB యొక్క మధ్యబిందువు M.
(i) AC పై D ఒక బిందువు అనుకొనుము. AC యొక్క మధ్య బిందువు D’ అనుకొనుము.
∴ AD’ = D’C
BC కి సమాంతరంగా గల రేఖ D’M.
కాని దత్తాంశం ప్రకారము DM, BC కి సమాంతర రేఖ. దీనిని బట్టి ఒక బిందువు M గుండా పోవు రెండు రేఖలు ఒక రేఖకు సమాంతరము అని నిరూపితమైనది. ఇది అసంభవము.
∴ D’ అనునది Dతో ఏకీభవిస్తుంది.
∴ AC మధ్య బిందువు ‘D’ అగును.
(ii) సమస్య (i) నుండి DM // BC అదే విధముగా \(\angle \mathrm{ADM}=\angle \mathrm{ACB}\) = 90° (సదృశ్యకోణాలు)
⇒ MD ⊥ AC
(iii) ΔADM మరియు ΔCDM లలో
AD = CD [∵ సమస్య (i) నుండి AC మధ్య బిందువు D]
\(\angle \mathrm{ADM}=\angle \mathrm{MDC}\) (∵ ప్రతీ కోణము 90°)
DM = DM (ఉమ్మడి భుజము)
∴ ∆ADM ≅ ∆CDM (భు.కో.భు. నియమం ప్రకారం)
⇒ CM = MA (CPCT)
⇒ CM = \(\frac {1}{2}\) AB (∵ AB మధ్య బిందువు M)
∴ CM = MA = \(\frac {1}{2}\) AB