AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.2

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson Areas Exercise 11.2

Question 1.
The area of parallelogram ABCD is 36cm². Calculate the height of parallelogram ABEF if AB = 4.2 cm.

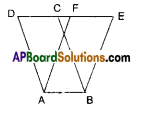
Solution:
Area of □ABCD = 36 cm²
AB = 4.2 cm
then □ABCD = AB X Height
[ ∵ base x height]
36 = 4.2 x h
∴ h = \(\frac { 36 }{ 4.2 }\)
But □ ABCD and □ ABEF are on the same base and between the same parallels.
∴ □ABCD = □ABEF
□ABEF = base x height = AB x height
∴ height = \(\frac { 36 }{ 4.2 }\) = 8.571cm 5

Question 2.
ABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm; AE = 8 cm and CF = 12 cm. Find AD.

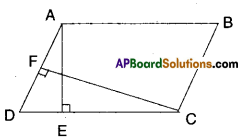
Solution:
Area of parallelogram = base x height
AB x AE = AD x CF
⇒ 10 x 8 = 12 x AD
⇒ AD = \(\frac{10 \times 8}{12}\) = 6.666 ……….
∴ AD ≅ 6.7 cm

Question 3.
If E, F, G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar (EFGH) = \(\frac { 1 }{ 2 }\) ar (ABCD).

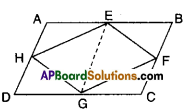
Solution:
Given that □ABCD is a parallelogram.
E, F, G and H are the midpoints of the sides.
Join E, G.
Now
ΔEFG and □EBCG he on the same base EG and between the same parallels
EG // BC.
∴ ΔEFG = \(\frac { 1 }{ 2 }\)□EBCG ……………(1)
Similarly,
ΔEHG = \(\frac { 1 }{ 2 }\)□EGDA …………….(2)
Adding (1) and (2);
ΔEFG + ΔEHG = \(\frac { 1 }{ 2 }\) □EBCG + \(\frac { 1 }{ 2 }\) □EGDA
□EFGH = \(\frac { 1 }{ 2 }\)[□EBCG +□ EGDA]
□EFGH = \(\frac { 1 }{ 2 }\) [□ABCD]
Hence proved.

Question 4.
What figure do you get, if you join ΔAPM, ΔDPO, ΔOCN and ΔMNB in the example 3 ?
Solution:

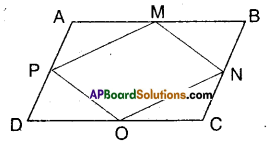
□ABCD is a rhombus.
M, N, O and P are the midpoints of its sides. By joining ΔAPM, ΔDPO, ΔOCN and ΔMNB we get the figure shown by shaded region.

Question 5.
P and Q are any two points lying on the sides DC and AD .respectively of a parallelogram ABCD. Show that ar (ΔAPB) = ar (ΔBQC).

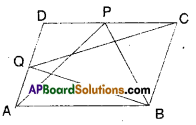
Solution:
ΔAPB and □ABCD are on the same base
AB and between the same parallel lines
AB//CD.
∴ ΔAPB = \(\frac { 1 }{ 2 }\) □ABCD …………… (1)
Also ΔBCQ and □BCDA are on the same base BC and between the same paral¬lel lines BC//AD.
∴ ΔBCQ = \(\frac { 1 }{ 2 }\) □BCDA …………….. (2)
But □ABCD and □BCDA represent same parallelogram.
∴ΔAPB = ΔBCQ [from (1) & (2)]

Question 6.
P is a point in the interior of a parallelogram ABCD. Show that
i) ar (ΔAPB) + ar (ΔPCD) = \(\frac { 1 }{ 2 }\)ar(ABCD)
(Hint : Through P, draw a line paral¬lel to AB)

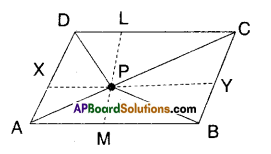
Solution:
□ABCD is a parallelogram.
P is any interior point.
Draw a line \(\overline{\mathrm{XY}}\) parallel to AB through P.
Now ΔAPB = \(\frac { 1 }{ 2 }\) □AXYB ……………(1)
[∵ ΔAPB, □AXYB lie on the same base AB and beween AB//XY]
Also ΔPCD = \(\frac { 1 }{ 2 }\) □CDXY ………………… (2)
[ ∵ ΔPCD; □CDXY lie on the same
base CD and between CD//XY]
Adding (1) & (2), we get
Δ APB + ΔPCD = \(\frac { 1 }{ 2 }\) □AXYB + \(\frac { 1 }{ 2 }\) □CDXY
= \(\frac { 1 }{ 2 }\) [□ AXYB + □ CDXY] [from the fig.)
= \(\frac { 1 }{ 2 }\) □ABCD
Hence Proved.

(ii) ar (ΔAPD) + ar (ΔPBQ = ar (ΔAPB) + ar (ΔPCD)
Solution:
Draw LM // AD.
ΔAPD + ΔPBC = \(\frac { 1 }{ 2 }\) □AMLD + \(\frac { 1 }{ 2 }\) □BMLC
= \(\frac { 1 }{ 2 }\) [□AMLD + \(\frac { 1 }{ 2 }\) BMLC].
= \(\frac { 1 }{ 2 }\) □ABCD
= ΔAPB +ΔPCD [from(i)]
Hence proved.
[ ∵ ΔAPD, □AMLD are on same base AD and between same parallels AD and LM]

Question 7.
Prove that the area of a trapezium is half the sum of the parallel sides mul¬tiplied by the distance between them.
Solution:

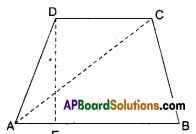
Let □ABCD is a trapezium; AB//CD and
DE ⊥ AB
□ABCD = ΔABC + ΔADC
= \(\frac { 1 }{ 2 }\) AB x DE + \(\frac { 1 }{ 2 }\) DC x DE
[∵ Δ = \(\frac { 1 }{ 2 }\) x base x height]
= \(\frac { 1 }{ 2 }\) x DE [AB + DC]
Hence proved.

Question 8.
PQRS and ABRS are parallelograms and X is any point on the side BR.
Show that

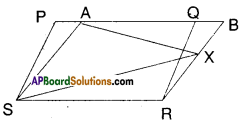
i) ar (PQRS) = ar (ABRS)
Solution:
□PQRS and □ABRS are on the same base SR and between the same parallels SR//PB.
∴ □PQRS = □ABRS

ii) ar (ΔAXS) = \(\frac { 1 }{ 2 }\) ar (PQRS)
Solution:
From (1) □PQRS = □ABRS
And □ABRS and ΔAXS are on the same base AS and between the same paral¬lels AS//BR.
∴ ΔAXS = \(\frac { 1 }{ 2 }\) □ABRS
= \(\frac { 1 }{ 2 }\) □PQRS from (1)
Hence proved.

Question 9.
A farmer has a held in the form of a parallelogram PQRS as shown in the figure. He took the midpoint A on RS and joined it to points P and Q. In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow groundnuts which are equal to the sum of pulses and paddy. How should he sow ? State reasons.

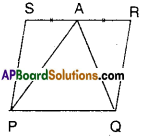
Solution:
From the figure ΔAPQ, □PQRS are on the same base PQ and between the same parallels PQ//SR.
∴ ΔAPQ = \(\frac { 1 }{ 2 }\)□PQRS
⇒ □PQRS – AAPQ = \(\frac { 1 }{ 2 }\)□PQRS
∴ \(\frac { 1 }{ 2 }\)□PQRS = ΔASP + ΔARQ
∴ The farmer may sow groundnuts on ΔAPQ region.
The farmer may sow pulses on ΔASP region.
The farmer may sow paddy on ΔARQ region.

Question 10.
Prove that the area of a rhombus is equal to half of the product of the diagonals.

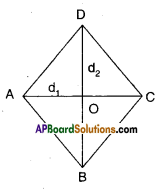
Solution:
Let □ABCD be a Rhombus.
d₁, d₂ are its diagonals bisecting at ‘O’
We know that d₁ ⊥ d₁
∴ ΔABC = \(\frac{1}{2} \mathrm{~d}_{1} \cdot\left(\frac{\mathrm{d}_{2}}{2}\right)\)
[∵ base = d₁; height = \frac{\mathrm{d}_{2}}{2}[/latex] ]
ΔADC = \(\frac{1}{2} \mathrm{~d}_{1} \cdot\left(\frac{\mathrm{d}_{2}}{2}\right)\)
[ ∵ base = d₁;height= \(\frac{\mathrm{d}_{2}}{2}\)]
∴ □ABCD = ΔABC + ΔADC
= \(\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{4}+\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{4}=\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{2}\)
Hence Proved.