SCERT AP 9th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.1
ప్రశ్న1.
a) ఏవైనా మూడు అకరణీయ సంఖ్యలు రాయండి.
సాధన.
\(\frac{3}{4}, \frac{5}{9}, \frac{2}{7}\)
b) అకరణీయ సంఖ్యను మీ సొంత మాటలలో వివరించండి.
సాధన.
\(\frac{\mathrm{p}}{\mathrm{q}}\) రూపంలో వ్యక్తపరచగలిగిన ఏ సంఖ్యనైనా అకరణీయ సంఖ్య అంటారు.
ఉదా: \(\frac{3}{5}, \frac{-4}{9}, \frac{5}{6}, \ldots \ldots \ldots\)
ప్రశ్న2.
కింది వాక్యాలకు ఒక్కొక్క ఉదాహరణను ఇవ్వండి.
i) అకరణీయ సంఖ్య అయి పూర్ణ సంఖ్య కాని సంఖ్య.
సాధన.
\(\frac {7}{11}\)
ii) పూర్ణాంకమయి సహజ సంఖ్య కాని సంఖ్య.
సాధన.
‘0’ (సున్న)
iii) పూర్ణ సంఖ్యయై పూర్ణాంకం కాని సంఖ్య.
సాధన.
-8
iv) సహజ సంఖ్య, పూర్ణాంకము, పూర్ణ సంఖ్య మరియు అకరణీయ సంఖ్య అన్నీ అయ్యే సంఖ్య.
సాధన.
5
v) పూర్ణ సంఖ్యయై సహజ సంఖ్య కాని సంఖ్య.
సాధన.
– 4
![]()
ప్రశ్న3.
1 మరియు 2ల మధ్యగల ఐదు అకరణీయ సంఖ్యలు కనుగొనండి.
సాధన.
1 మరియు 2ల మధ్య 5 అకరణీయ సంఖ్యలుండాలి.
కావున 1 మరియు 2 ల హారాలను 1 + 5 = 6 గా వ్రాస్తాము.
∴ 1 = 1 × \(\frac {6}{6}\) మరియు 2 = \(\frac{2 \times 6}{6}=\frac{12}{6}\)
ఇప్పుడు
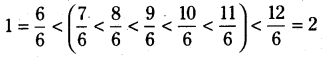
ప్రశ్న4.
\(\frac {2}{3}\) మరియు \(\frac {3}{5}\) ల మధ్య మూడు అకరణీయ సంఖ్యలుంచుము.
సాధన.
a, b ల మధ్యగల అకరణీయ సంఖ్య \(\frac{a+b}{2}\) కావున
అదే విధముగా a = \(\frac {2}{3}\), b = \(\frac {3}{5}\) అనుకొనుము.

ప్రశ్న5.
\(\frac {8}{5}\) మరియు \(\frac {-8}{5}\) లను సంఖ్యారేఖపై సూచించండి.
సాధన.

సోపానం-1 : – 3, – 2, – 1, 0, 1, 2, 3 లను సూచిస్తూ ఒక సంఖ్యారేఖను గీయండి.
సోపానం-2 : ఆ సంఖ్యారేఖ పై సున్నాకు కుడి మరియు ఎడమవైపు ప్రతి యూనిట్ ను ఐదు సమాన భాగాలుగా చేయండి.
సోపానం-3 : సున్నా నుండి కుడివైపు గల ఎనిమిదవ బిందువు \(\frac {8}{5}\)ను మరియు ఎడమవైపు గల ఎనిమిదవ బిందువు \(\frac {-8}{5}\)ను సూచిస్తుంది.
![]()
ప్రశ్న6.
కింది అకరణీయ సంఖ్యలను దశాంశ రూపంలో రాయండి.
I. i) \(\frac {242}{1000}\)
సాధన.
\(\frac {242}{1000}\) = 0.242
ii) \(\frac {354}{500}\)
సాధన.
\(\frac {354}{500}\)
= \(\frac{354 \times 2}{500 \times 2}\)
= \(\frac {708}{1000}\)
= 0.708
iii) \(\frac {2}{5}\)
సాధన.
\(\frac {2}{5}\)
= \(\frac{2 \times 2}{5 \times 2}\)
= \(\frac {4}{10}\)
= 0.4
iv) \(\frac {115}{4}\)
సాధన.

∴ \(\frac {115}{4}\) = 28.75
II. i) \(\frac {2}{3}\)
సాధన.

∴ \(\frac {2}{3}\) = 0.6666 ……. = \(0 . \overline{6}\)
ii) \(\frac {-25}{36}\)
సాధన.

∴ \(\frac {-25}{36}\) = -0.6944 ….. = \(-0.69 \overline{4}\)
iii) \(\frac {22}{7}\)
సాధన.
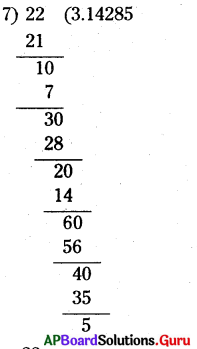
∴ \(\frac {22}{7}\) = 3.14285 ……
iv) \(\frac {11}{9}\)
సాధన.
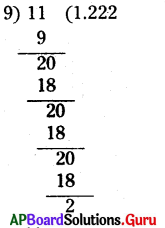
∴ \(\frac {11}{9}\) = 1.222 …… = \(1 . \overline{2}\)
![]()
ప్రశ్న7.
కింది వాటిని \(\frac{\mathrm{p}}{\mathrm{q}}\) (p, q లు పూర్ణసంఖ్యలు మరియు – q ≠ 0) రూపంలో రాయండి.
i) 0.36
సాధన.
0.36 = \(\frac{36}{100}=\frac{9}{25}\)
ii) 15.4
సాధన.
15.4 = \(\frac{154}{10}=\frac{77}{5}\)
iii) 10.25
సాధన.
10.25 = \(\frac{1025}{100}=\frac{41}{4}\)
iv) 3.25
సాధన:
3.25 = \(\frac{325}{100}=\frac{13}{4}\)
ప్రశ్న8.
కింది వాటిని \(\frac{\mathrm{p}}{\mathrm{q}}\) (p, q లు పూర్ణసంఖ్యలు మరియు q ≠ 0) రూపంలో రాయండి.
i) \(0 . \overline{5}\)
సాధన.
x = \(0 . \overline{5}\) = 0.5555……… అనుకొనుము.
అవధి ‘1’ కావున ఇరువైపులా 10 చే గుణించగా

∴ \(0 . \overline{5}\) యొక్క \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపము \(\frac {5}{9}\) అగును.
ii) \(3 . \overline{8}\)
సాధన.
x = \(3 . \overline{8}\) అనుకొనుము.
x = 3.888 ………
అవధి ‘1’ కావున ఇరువైపులా 10 చే గుణించగా

∴ \(3 . \overline{8}\) యొక్క \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపము \(\frac {35}{9}\) అగును.
iii) \(0 . \overline{36}\)
సాధన.
x = \(0 . \overline{36}\) అనుకొనుము.
x = 0.363636 …………
అవధి ‘2’ కావున ఇరువైపులా 100 చే గుణించగా

∴ \(0 . \overline{36}\) యొక్క \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపము \(\frac {4}{11}\) అగును.
iv) \(0 . \overline{36}\)
సాధన.
x = \(3.12 \overline{7}\) అనుకొనుము.
x = 3.12777 ……….
అవధి ‘1’ కావున ఇరువైపులా 10 చే గుణించగా

∴ \(3.12 \overline{7}\) యొక్క \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపము \(\frac {563}{180}\) అగును.
![]()
ప్రశ్న9.
కింద ఇచ్చిన ఏ సంఖ్యలు అంతమయ్యే దశాంశాలో భాగహారం చేయకుండానే గుర్తించండి.
i) \(\frac{3}{25}\)
సాధన.
ఇచ్చిన సంఖ్య యొక్క హారంను గమనించుము.
హారంలో ‘2’ లేక ‘5’ లేక “2 మరియు 5”ల లబ్దముగాని వుంటే ఆ అకరణీయ సంఖ్య అంతమయ్యే దశాంశమగును.
∴ ఇచ్చిన సంఖ్య యొక్క హారము 25 = 5 × 5
కావున \(\frac{3}{25}\) అంతమగు దశాంశము.
ii) \(\frac{11}{18}\)
సాధన.
ఇచ్చిన సంఖ్య హారము 18 = 2 × 3 × 3
∴ \(\frac{11}{18}\) అంతము కాని దశాంశము.
iii) \(\frac{13}{20}\)
సాధన.
ఇచ్చిన సంఖ్య యొక్క హారము 20 = 2 × 2 × 5
∴ \(\frac{13}{20}\) అంతమగు దశాంశము.
iv) \(\frac{41}{42}\)
సాధన.
ఇచ్చిన సంఖ్య యొక్క హారము 42 = 2 × 3 × 7
∴ \(\frac{41}{42}\) అంతము కాని దశాంశము.