Students can go through AP Board 9th Class Maths Notes Chapter 4 Lines and Angles to understand and remember the concepts easily.
AP State Board Syllabus 9th Class Maths Notes Chapter 4 Lines and Angles
→ A ray is a part of line. It begins at a point and goes on endlessly in a specified direction.
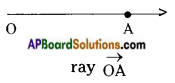
→ A part of a line with two end points is called a line segment.

![]()
→ Points on the same line are called collinear points.
![]()
→ The angle is formed by rotating a ray from an initial position to a terminal position.
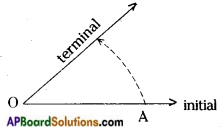
→ One complete rotation makes an angle 360°.
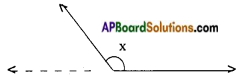
→ Angles are named according to their measure.
Obtuse angle 90° < x < 180°.
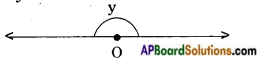
→ Straight angle y = 180°
→ Reflex angle 180° < z < 360°

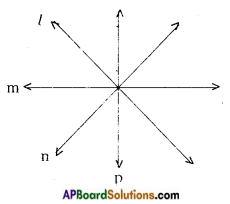
→ If two lines have no common points, they are called parallel lines. In the figure l // m.

→ If two lines have a common point then they are called intersecting lines.
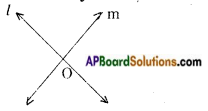
→ Three or more lines meet at a point are called concurrent lines.
![]()
→ Two angles are said to be supplementary angles if their sum is 180°.
E.g.: (100°, 80°), (110°, 70°), (120°, 60°), (179°, 1°), (90°, 90°) etc.
→ The supplementary angle to x° is given by (180° – x°).
→ Two angles are said to be complementary if their sum is 90°.
→ The complementary angle to x° is (90° – x°).
E.g.: (89°, 1°), (70°, 20°), (60°, 30°) etc.
→ Two angles are said to be form a pair of adjacent angles if they have a common arm and lie on the either sides of the common arm.
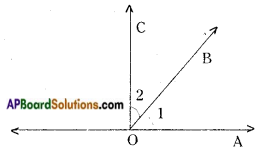
∠1 and ∠2 are a pair of adjacent angles with OB as their common arm.
→ A pair of adjacent angles are said to be a linear pair of angles if their sum is 180°. ∠1 + ∠2 = 180°
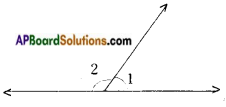
→ When a pair of lines meet at a point, they form four angles. The two pairs of angles which have no common arm are called vertically opposite angles.
In the figure (∠1, ∠3) and (∠2, ∠4) are the pairs of vertically opposite angles.

→ When two lines intersect, the pairs of vertically opposite angles thus formed are equal a = c and b = d. (from the figure)

![]()
→ When a pair of lines intersected by a transversal, there forms eight angles.
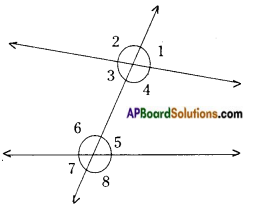
→ When a pair of parallel lines intersected by a transversal the pairs of a) alternate interior angles b) corresponding angles c) alternate exterior angles are equal and the interior / exterior angles on the same side of the transversal are supplementary.
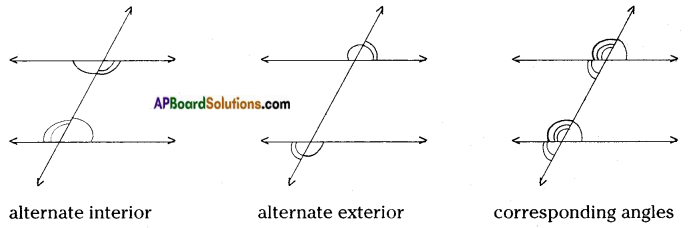
→ Lines which are parallel to same line are parallel to each other.
![]()
→ The sum of the interior angles of a triangle is 180°.
→ If one side of a triangle is produced, then the exterior angle thus formed is equal to the sum of the two interior opposite angles.