AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.4 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.4
![]()
Question 1.
Rice costing ₹480 is needed for 8 members for 20 days. What is the cost of rice required for 12 members for 15 days?
Solution:
Method – 1: Number of men and rice required to them are in inverse proportion.
Number of men ∝ \(\frac{1}{\text { No. of days }}\)
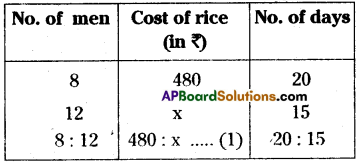
⇒ Compound ratio of 8:12 and 20: 15
= \(\frac{8}{12}=\frac{20}{15}\) = \(\frac{8}{9}\) …………….. (2)
From (1), (2)
480 : x = 8 : 9
⇒ \(\frac{480}{x}=\frac{8}{9}\)
⇒ x = \(\frac{480 \times 9}{8}\) = ₹540
∴ The cost of required rice is ₹ 540
![]()
Method – II :
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M1 = No. of men
D1 = No .of days
W1 = Cost of rice
∴ M1 = 8
D1 = 20
W1 = ₹ 480
M2 = 12
D2 = 15
W2 = ? (x)

⇒ x = 45 x 12 = ₹ 540
The cost of required rice = ₹ 540/-
![]()
Question 2.
10 men can lay a road 75 km. long in 5 days. In how many days can 15 men lay a road 45 km. long?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
∴ M1 = 10
D1 = 5
W1 = 75
M2 = 15
D2 = ?
W2 = 45
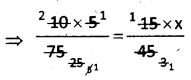
∴ x = 2
∴ No. of days are required = 2
Question 3.
24 men working at 8 hours per day can do a piece of work in 15 days. In how many days can 20 men working at 9 hours per day do the same work?
Solution:
M1D1H1 = M2D2H2
∴ M1 = 24
D1 = 15 days
H1 = 8 hrs
M2 = 20
D2 = ?
H2 = 9 hrs
⇒ 24 × 15 × 8 = 20 × x × 9
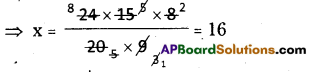
∴ No. of days are required = 16
[ ∵ No. of men and working hours are in inverse]
![]()
Question 4.
175 men can dig a canal 3150 m long in 36 days. How many men are required to dig a canal 3900 m. long in 24 days?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M1 = 175
D1 = 36
W1 = 3150
M2 = ?
D2 = 24
W2 = 3900
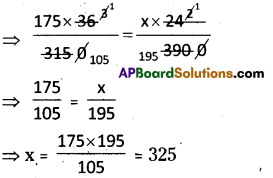
∴ No. of workers are required = 325
![]()
Question 5.
If 14 typists typing 6 hours a day can take 12 days to complete the manuscript of a book, then how many days will 4 typists, working 7 hours a day, can take to do the same job?
Solution:
M1D1H1 = M2D2H2
M1 = 14
D1 = 12 days
H1 = 6
M2 = 4
D2 = ?
H2 = 7
⇒ 14 × 12 × 6 = 4 × x × 7
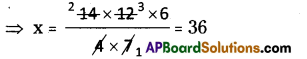
⇒ x = 36
∴ No. of days are required = 36
[ ∵ No of men and working hours are in inverse proportion]