AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.3 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.3
![]()
Question 1.
Siri has enough money to buy 5 kg of potatoes at the price of ₹ 8 per kg. How much can she buy for the same amount if the price is increased to ₹ 10 per kg?
Solution:
Number of kgs of potatoes to their price are in inverse proportion.
∴ x1y1 = x2 y2
⇒ 8 × 5 = 10 × x
⇒ x = \(\frac{8 \times 5}{10}\) = 4 kgs
∴ 4 kgs of potatoes will be purchased at the rate of ₹ 10 per kg.
Question 2.
A camp has food stock for 500 people for 70 days. ¡f200 more people join the camp, how long will the stock last?
Solution:
Number of persons and their food stock are in inverse proportion.
⇒ x1y1 = x2 y2 (Let y2 = x say)
⇒ 500 × 70 = (500 + 200) × x
⇒ x = \(\frac{500 \times 70}{700}\) = 5 × 10
∴ x = 50
∴ The food will be stock for (200 + 500) 700 men = 50 days
![]()
Question 3.
36 men can do a piece of work in 12 days. ¡n how many days 9 men can do the same work?
Solution:
Number of workers and number of days are in inverse proportion
∴ x1y1 = x2 y2 let y2 = x (say)
= 36 × 12 = 9 × x
x = \(\frac{36 \times 12}{9}\) = 48
∴ x = 48 days
Question 4.
A cyclist covers a distance of28 km in 2 hours. Find the time taken by him to cover a distance of 56 km with the same speed.
Solution:
Time and distance are in direct proportion.
∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) , Let y2 = x (say)
⇒ \(\frac{28}{2}\) = \(\frac{56}{x}\)
⇒ x = \(\frac{56}{14}\)
∴ x = 4 hours
![]()
Question 5.
A ship can cover a certain distance in 10 hours at a speed of 16 nautical miles per hour. By how much should its speed be increased so that it takes only 8 hours to cover the same distance? (A nautical mile in a unit of measurement used at sea distance or sea water i.e. 1852 metres).
Solution:
Speed and distance are in inverse proportion.
⇒ x1y1 = x2 y2 , Let x2 = x (say)
⇒ 16 × 10 = x × 8
⇒ x = \(\frac{16 \times 10}{8}\)= 20
∴ x = 20
∴ The speed to be increased
= 20 – 16 = 4 nautical miles
Question 6.
5 pumps are required to fill a tank in 1\(\frac { 1 }{ 2 }\) hours. How many pumps of the same type are used to fill the tank in half an hour.
Solution:
Number of pumps and time to fill the tanks are in inverse proportion.
⇒ x1y1 = x2 y2
⇒ 5 × 1\(\frac { 1 }{ 2 }\) = x x 1\(\frac { 1 }{ 2 }\)
⇒ 5 × \(\frac { 3 }{ 2 }\) = x x \(\frac { 1 }{ 2 }\)
⇒ x = 5 × 3 = 15
∴ Number of pumps required = 15
![]()
Question 7.
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Solution:
Number of workers and time are in inverse proportion.
⇒ x1y1 = x2 y2
⇒ 15 × 48 = x × 30
⇒ x = \(\frac{15 \times 48}{30}\) = 24
∴ Number of workers required = 24
Question 8.
A School has 8 periods a day each of45 minutes duration. How long would each period become ,if the school has 6 periods a day? ( assuming the number of school hours to be the same)
Solution:
Time and number of periods are in inverse proportion.
⇒ x1y1 = x2 y2
⇒ 45 × 8 = x × 6
⇒ \(\frac{45 \times 8}{6}\)
⇒ 60 minutes
Question 9.
If z varies directly as xand inversely as y. Find the percentage increase in z due to an increase of 12% in x and a decrease of 20% in y.
Solution:
Given that
z varies directly as x and inversely as y So, z ∝ x (1); z ∝ 1/y ……………… (2)
From (1) & (2), z ∝ \(\frac{\mathrm{x}}{\mathrm{y}}\)
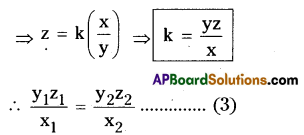
Let x1 = 100x, x2 = 112x
(∵ It increases 12%)
y1 = 100y, y2 = 80y
(∵ It decreases 20%)
From (3),
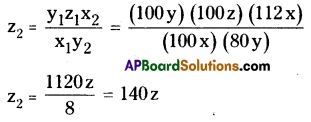
∴ z is increased in 40%
![]()
Question 10.
If x + 1 men will do the work in x + 1 days, find the number of days that (x + 2) men can finish the same work.
Solution:
Number of workers and number of days are in inverse proportion.
⇒ x1y1 = x2 y2
⇒ (x + 1) (x + 1) = (x + 2) x k
⇒ k = \(\frac{(x+1)(x+1)}{(x+2)}\)
∴ k = \(\frac{(x+1)^{2}}{(x+2)}\)
Question 11.
Given a rectangle with a fixed perimeter of 24 meters, if we increase the length by 1 m the width and area will vary accordingly. Use the following table of values to look at how the width and area vary as the length varies.
What do you observe? Write your observations in your note books

Solution:
