AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.1
![]()
Question 1.
The cost of 5 meters of a particular quality of cloth is ₹ 210. Find the cost of(i) 2 (ii) 4
(iii) 10 (iv) 13 meters of cloth of the same quality.
Solution:
The cost of 5 m of a cloth = ₹ 210
The length of a cloth and its price are in direct proportion.
i) \(\frac{\mathrm{x}_{1}}{\mathrm{y}_{1}}=\frac{\mathrm{x}_{2}}{\mathrm{y}_{2}}\)
Here x1 = 5, y1 = 210
x2 = 2, y2 = ?
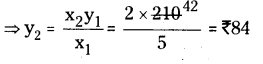

![]()
Question 2.
Fill the table.

Solution:

Question 3.
48 bags of paddy costs ₹ 16, 800 then find the cost of 36 bags of paddy.
Solution:
Number of bags of paddy and their cost are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) , x1 = 16,800
x2 = 36 y2 = ?
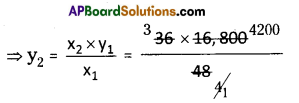
= 3 × 4200
y2 = ₹ 12600
∴ The cost of 36 bags of paddy = ₹ 12600
Question 4.
The monthly average expenditure of a family with 4 members is 2,800. Find the
monthly average expenditure ofa family with only 3 members.
Solution:
Number of family members and their expenditure are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) , x1 = 4
y1 = 2,800
x2 = 3 y2 = ?
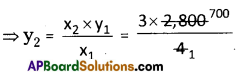
= 3 × 700 = 2100
y2 = ₹ 2100
The expenditure for 3 members = ₹ 2100
![]()
Question 5.
In a ship of length 28 m, height of its mast is 12 m. If the height of the mast in its model is
9 cm what is the length of the model ship?
Solution:
The length of ship and the height of its mast are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) , x1 = 28
y1 = 12
x2 = ? y2 = 9
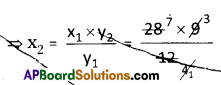
x2 = 7 × 3 = 21
∴ The length of model ship = 21 m
Question 6.
A vertical pole of 5.6 m height casts a shadow 3.2 m long. At the same time find (j) the
length of the shadow cast by another pole 10.5 m high (ii) the height of a pole which casts
a shadow 5m long.
Solution:
length of a vertical pole and length of its shadow are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
i) x1 = 5.6
y1 = 3.2
x2 = 10.5 y2 = ?
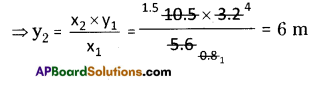
∴The length of the shadow = 6 cm
ii) x1 = 5.6 m x2 = ?
y1 = 3.2 m y2 = 5
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
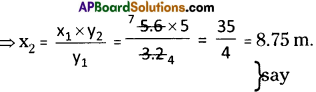
∴ x2 = 8.75
![]()
Question 7.
A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution:
Time and distance are in direct proportion
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
x1 = 14 km , x2 = ?
y1 = 25min = \(\frac{25}{60} \mathrm{hr}=\frac{5}{12} \mathrm{hr}\) = y2 = 5hrs
⇒ \(x_{2}=\frac{x_{1} \times y_{2}}{y_{1}}=\frac{14 \times 5}{5}=\frac{14 \times \not 5 \times 12}{\not 5}\)
= 168 km
∴ Lorry travelled in 5 hrs = 168km
Question 8.
If the weight of 12 sheets of thick paper is 40 grams, how many sheets of the same paper would weigh 16 \(\frac { 2 }{ 3 }\) kilograms?
Solution:
Number of pages and their weight are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
x1 = 12 km , x2 = ?
y1 = 40 gm
y2 = 16 \(\frac { 2 }{ 3 }\) gm = \(\frac { 50 }{ 3 }\) x 1000 gm
= \(\frac { 50000 }{ 3 }\) gm
From (1)
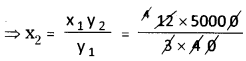
∴ Number of pages = 5000
![]()
Question 9.
A train moves at a constant speed of 75 km/hr.
(i) How far will it travel in 20 minutes?
(ii) Find the time required to cover a distance of 250 km.
Solution:
Speed of the train = 75 km/hr
i) The distance travelled in 20 min.
d = s x t = 75 x 20 min
= 75 x = 25 km
= \(75 \times \frac{20}{60}=\frac{75}{3}\) = 25 km
ii) Time taken to travel 250 km
t = \(\frac{d}{s}=\frac{250}{75}\)
t = \(\frac{10}{3}\) hrs
Question 10.
The design of a microchip has the scale 40:1. The length of the design is 18cm, find the actual length of the micro chip?
Solution:
The scale of the design of a microchip
= 40 : 1
The length of the design = 18 cm
The actual length of microchip = ?
The length of the design and actual length of the microchip are in direct proportion.
⇒ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
x1 = 40 km , x2 = 18
y1 = 1
y2 = ?
⇒ \(\frac{40}{1}=\frac{18}{y_{2}}\)
⇒ \(\frac{18}{40}=\frac{9}{20}\) cm
∴ The original (actual) length of the microchip = [latexs]\frac{9}{20}[/latex]cm
![]()
Question 11.
The average age of consisting doctors and lawyers is 40. If the doctors average age is 35 and the lawyers average age is 50, fmd the ratio of the number of doctors to the number of lawyers.
Solution:
Let the number of doctors = x
Number of lawyers = y
The average age of doctors = 35
The total age of doctors = 35 × x
= 35 x years
The average age of lawyers = 50
∴ The total age of lawyers = 50 x y
= 50y
According to the sum
\(\frac{35 x+50 y}{x+y}\) = 40
⇒ 35x + 50y = 40x + 40y
⇒ 40x – 35x = 50y – 40y
⇒ 5x = lOy
⇒ \(\frac{x}{y}=\frac{10}{5}\) (or)
x : y = 2 : 1
∴ The ratio of number of doctors to lawyers = 2:1