SCERT AP 7th Class Maths Solutions Pdf Chapter 6 Algebraic Expressions Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 6th Lesson Algebraic Expressions Unit Exercise
Question 1.
Fill in the blanks:
(i) The constant term in the expression a + b + 1 is ………………..
Answer:
1.
(ii) The variable in the expression 3x – 8 is ………………..
Answer:
x
![]()
(iii) The algebraic term in the expression 2d – 5 is ………………..
Answer:
2d
(iv) The number of terms in the expression ……………….. p2 – 3pq + q is
Answer:
3
(v) The numerical coefficient of the term – ab is …………………..
Answer:
– 1
Question 2.
Write below statements are True or False:
(i) \(\frac{3 x}{9 y}\) is a binomial.
Answer:
False
(ii) The coefficient of b in – 6abc is – 6a.
Answer:
False
(iii) 5pq and – 9qp are like terms.
Answer:
True
(iv) The sum of a + b and 2a + 7 is 3a + 7b.
Answer:
False
(v) When x = – 2, then the value of x + 2 is 0.
Answer:
True.
Question 3.
Identify like terms among the following:
3a, 6b, 5c, – 8a, 7c, 9c, – a, \(\frac{2}{3}\)b, \(\frac{7 c}{9}\), \(\frac{a}{2}\).
Answer:
Given terms are
3a, 6b, 5c, – 8a, 7c, 9c, – a, \(\frac{2}{3}\)b, \(\frac{7 c}{9}\), \(\frac{a}{2}\)
Like terms: 3a, – 8a, – a, \(\frac{a}{2}\)
6b, \(\frac{2}{3}\)b
5c, 7c, 9c, \(\frac{7 c}{9}\)
![]()
Question 4.
Arjun and his friend George went to a stationary shop. Arjun bought 3 pens and 2 pencils whereas George bought one pen and 4 pencils. If the price of each pen and pencil is ₹ x and ₹ y respectively, then find the total bill amount in x and y.
Answer:
Given cost of each pen is ₹ x and cost of each pencil is ₹ y .
Arjun bought 3 pens and 2 pencils. Cost of 3 pens = 3 × ₹ x = ₹ 3x
Cost of 2 pencils = 2 × ₹y = ₹ 2y
Amount paid by Arjun = 3x + 2y = ₹ (3x + 2v)
George bougth one pen and 4 pencils.
Cost of 1 pen = 1 × ₹ x = ₹ x
Cost of 4 pencils = 4 × ₹ y = ₹ 4y
Amount paid by George = x + 4y = ₹(x + 4y)
Total bill amount
= Arjun amout + George amount
= (3x + 2y) + (x + 4y)
= 3x + 2y + x + 4y
= 3x + x + 2y + 4y
= (3 + 1)x + (2 +4)y
∴ Total bill amount = ₹ (4x + 6y)
Question 5.
Find the errors and correct the following :
(i) 7x + 4y = 11xy
Answer:
7x and 4y are not like terms and different variables x, y.
So, we should not add the coefficients.
(ii) 8a2 + 6ac = 14a3c
Answer:
8a2 and 6ac are not like terms. So, we should not add the coefficients.
(iii) 6pq2 – 9pq2 = 3pq2
Answer:
6pq2 – 9pq2 = (6 – 9)pq2
= – 3pq2
(iv) 15mn – mn = 15
Answer:
15mn – mn = (15 – 1) mn
= 14 mn
(v) 7 – 3a = 4a
Answer:
7 and 3a are not like terms.
So, we should not subtract the coefficient 7 and 3.
![]()
Question 6.
Add the expressions
(i) 9a + 4, 2 – 3a
Answer:
Given expressions are 9a + 4; 2 – 3a
Write the given expressions in standard form.
9a + 4, – 3a + 2.
The sum = (9a + 4) + (- 3a + 2)
= 9a + 4 – 3a + 2
= (9a – 3a) + (4 + 2)
= (9 – 3)a + 6
= 6a + 6
(ii) 2m – 7n, 3n + 8m, m + n
Answer:
Given expressions are
2m – 7n, 3n + 8m, m + n
Write the given expressions in standard form.
2m – 7n, 8m + 3n, m + n
The sum
= (2m 7n) + (8m + 3n) + (m + n)
= 2m – 7n + 8m + 3n + m + n
= (2m + 8m + m) + (- 7n + 3n + n)
= (2 + 8 + 1)m + (- 7 + 3 + 1)n
= 11 m + (- 3)n
= 11 m – 3n
Question 7.
Subtract:
(i) – y from y
Answer:
– y from y = y – (-y) = y + y = 2y
(ii) 18 pq from 25pq
Answer:
18pq from 2 5pq
= 25 pq – 18 pq
= (25 – 18) pq = 7pq
![]()
(iii) 6t + 5 from 1 – 9t
Answer:
Given expressions are (6t + 5), (1 – 9t)
Write the given expressions in the standard form (6t + 5); (- 9t + 1)
(6t + 5) from (- 9t + 1)
= (- 9t + 1) – (6t + 5)
= – 9t + 1 – 6t – 5
= (- 9t – 6t) + (1 – 5)
= (- 9 – 6) t + (- 4) = – 15t – 4
Question 8.
Simplify the following :
(i) t + 2 + t + 3 + t + 6- t- 6 + t
Answer:
Given t + 2 + t + 3+ t + 6 – t – 6 + t
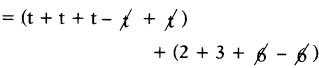
= 3t + 5
(ii) (a + b + c) + (2a + 3b – c) – (4a + b – 2c)
Answer:
Given (a + b + c) + (2a + 3b – c) – (4a + b – 2c)
= a + b + c + 2a + 3b – c – 4a – b + 2c
= (a + 2a – 4a) + (b + 3b – b) + (c – c + 2c)
= (1 + 2 – 4)a + (1 + 3 – 1)b + (1 – 1 + 2)c
= (- 1) a + 3b + 2c
= – a + 3b + 2c
(iii) x + (y + 1) + (x + 2) + (y + 3) + (x + 4) + (y + 5)
Answer:
Given x + (y + 1) + (x + 2) + (y + 3) + (x + 4) + (y + 5)
= x + y + 1 + x + 2 + y + 3 + x + 4 + y + 5
= (x + x + x) + (y + y + y) + (1 + 2 + 3 + 4 + 5)
= 3x + 3y + 15
Question 9.
The perimeter of a triangle is 8x2 + 7x – 9 and two of its sides are x2 – 3x + 4, 2x2 + x – 9 respectively, then find third side.
Answer:
Let the sides of triangle are A, B, C.
A = x2 – 3x + 4; B = 2x2 + x – 9 ; C = ?
Perimeter = 8x2 + 7x – 9
Perimeter of the triangle = A + B + C
To get the third side (C). subtract sum of A and B from the perimeter.
∴ C = Perimeter – (A + B)
So,
A + B = (x2 – 3x + 4) + (2x2 + x – 9)
= x2 – 3x + 4 + 2x2 + x – 9
= x2 + 2x2 – 3x + x +4 – 9
= (1 + 2) x2 + (- 3 + 1) x – 5
A + B = 3x2 – 2x – 5
Additive inverse of A + B is – (A + B)
– (A + B) = – (3x2 – 2x – 5) .
– (A + B) = – 3x2 + 2x + 5
C = perimeter + [- (A + B)]
= (8x2 + 7x – 9) + (- 3x2 + 2x + 5)
= 8x2 + 7x – 9 – 3x2 + 2x + 5
= 8x2 – 3x2 + 7x + 2x – 9 + 5
= (8 – 3) x2 + (7 + 2) x – 4
C = 5x2 + 9x – 4
∴ Third side is 5x2 + 9x – 4.
![]()
Question 10.
The perimeter of a rectangle is 2a3 – 4a2 – 12a + 10, if length is 3a2 – 4, find its breadth.
Answer:
Given length of rectangle l = 3a2 – 4 and breadth b = ?
Perimeter of a rectangle = 2a3 – 4a2 – 12a + 10
Perimeter of a rectangle
= 2(l + b)
= 2a3 – 4a2 – 12a + 10
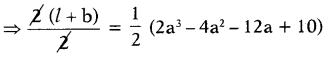
= \(\frac{1}{2}\) × 2(a3 – 2a2 – 6a + 5)
⇒ l + b = (a3 – 2a2 – 6a + 5)
⇒ l + b – l = (a3 – 2a2 – 6a + 5) – l
∴ b = (a3 – 2a2 – 6a + 5) – l
Additive inverse of 1 is – 1 = – (3a2 – 4)
∴ – l = – 3a2 + 4 .
b = (a3 – 2a2 – 6a + 5) + (- 1)
= (a3 – 2a2 – 6a + 5) + (- 3a2 + 4)
= a3 – 2a2 – 6a + 5 – 3a2 + 4
= a3 – 2a2 – 3a2 – 6a + 5 + 4
= a3 + (- 2 – 3) a2 – 6a + 9
= a3 + (- 5) a2 – 6a + 9
∴ Breadth of rectangle
= a3 – 5a2 – 6a + 9