SCERT AP 7th Class Maths Solutions Pdf Chapter 8 Exponents and Powers Ex 8.2 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 8th Lesson Exponents and Powers Ex 8.2
Question 1.
Simplify the following by using Laws of Exponents.
(i) 37 × 38
Answer:
37 × 38
We know am × an = am+n
37 × 38 = 37 + 8 = 315
∴ 37 × 38 =315
(ii) 92 × 90 × 93
Answer:
92 × 90 × 93
We know ap × aq × ar = p + q + r
92 × 90 × 93 = 92 + 0 + 3 = 95
∴ 92 × 90 × 93 = 95
(iii) (28)3
Answer:
(28)3
We know (am)n = amn
(28)3 = 28×3 =224
∴ (28)3 = 224
(iv) (a5)4
Answer:
(a5)4
We Know (am)n = amn
(a5)4 = a5×4 = a20
(a5)4 = a20
(v) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{3} \times\left(\frac{2}{5}\right)^{8}\)
Answer:

(vi) 75 ÷ 78
Answer:
75 ÷ 78
We know am = \(\frac{1}{a^{n-m}}\) (n>m)
75 ÷ 78 = \(\frac{1}{7^{8-5}}=\frac{1}{7^{3}}\)
∴ 75 ÷ 78 = \(\frac{1}{7^{3}}\)
(vii) \(\frac{(-6)^{9}}{(-6)^{5}}\)
Answer:
\(\frac{(-6)^{9}}{(-6)^{5}}\)
We Know am ÷ an = am-n(m > n)
\(\frac{(-6)^{9}}{(-6)^{5}}\) = (-6)9-5 = (-6)4
∴ \(\frac{(-6)^{9}}{(-6)^{5}}\) = (-6)4
(viii) (64 × 62) ÷ 65
Answer:
(64 × 62) ÷ 65
We know atm X a = a”
= (64+2) ÷ 65
= 66 ÷ 65
We know am ÷ an = am-n (m> n)
= 66-5 = 61 = 6
∴ (64 × 62) ÷ 65 = 6
(ix) \(\frac{5^{3}}{2^{3}}\)
Answer:
\(\frac{5^{3}}{2^{3}}\)
We know \(\frac{a^{m}}{b^{m}}=\left(\frac{a}{b}\right)^{m}\)
∴ \(\frac{5^{3}}{2^{3}}=\left(\frac{5}{2}\right)^{3}\)
(x) (-3)3 × (-3)10 × (-3)7
Answer:
(-3)3 × (-3)10 × (-3)7
we know ap . aq. ar = ap+q+r
(-3)3 × (-3)0 × (-3)7 = (-3)3+10+7
∴ (- 3)3 × (- 3)10 × (- 3)7 = (- 3)20
![]()
Question 2.
Simplify and express each of the following in Exponential form.
(i) \(\left(\frac{a^{5}}{a^{3}}\right)\) × a8
Answer:
\(\left(\frac{a^{5}}{a^{3}}\right)\) × a8
We Know \(\frac{a^{m}}{a^{n}}\) = am-n(m > n)
= (a5-3) × a8
= a2 × a8
We know am × an = am+n
= a2+8 = a10
∴ \(\left(\frac{a^{5}}{a^{3}}\right)\) × a8 = a10
(ii) 20 + 30 – 40
Answer:
20 + 30 – 40
We know a0 = 1
![]()
∴ 20 + 30 – 40 = 1
(iii) (23 × 2)2
Answer:
(23 × 2)2
We know am.an = am+n
(23 × 2)2 = (23+1)2 = (24)2
We know (am)n = am.n
= 24×2 = 28
∴(23 × 2)2 = 28
(iv) [(52)3 × 54] ÷ 57
Answer:
[(52)3 × 54] ÷ 57
We know (am) = am.n
= [52×3 × 54] ÷ 57
= [56 < 54] ÷ 57
We know am .an = am+n
= [56+4] ÷ 57
= 510 ÷ 57
We know am ÷ an = am-n (m > n)
= 510-7 = 53
∴ [(52)3 × 54] ÷ 57 = 53
Question 3.
Simplify \(\left(\frac{x^{a}}{x^{b}}\right) \times\left(\frac{x^{b}}{x^{c}}\right) \times\left(\frac{x^{c}}{x^{a}}\right)\)
Answer:
\(\left(\frac{x^{a}}{x^{b}}\right) \times\left(\frac{x^{b}}{x^{c}}\right) \times\left(\frac{x^{c}}{x^{a}}\right)\)

Question 4.
Find the value of the following.
(i) (-1)1000
Answer:
(-1)1000
(-1)1 = – 1
(-1)2 = – 1 × – 1 = + 1
(-1)3 = – 1 × -1 × -1 = – 1
(-1)4 = -1 × -1 × – 1 × – 1 = + 1
(-1)5 = -1 × -1 × -1 × -1 × -1 = -1
(-1)100 = -1 × -1 × -1 × ………… 100 times = + 1
So, (-1)odd number = -1 and
(-1)even number = + 1
Here 1000 is even number
So, (-1)1000 = + 1
(ii) (1)250
Answer:
1250 = 1 × 1 × 1 ……… 250 times = 1
∴ 1250 = 1
(iii) (1)121
Answer:
1121 = -1 × -1 × -1 ……..(121 times)
Here 121 is an odd number
So, (1)121 = – 1
(iv) (10000)0
Answer:
(10000)0
we know a0 = 1
So, (10000)0 = 1
Question 5.
If 75 × 73x = 720 then find the value of ’x’.
Answer:
Given, 75 × 73x = 720
W know am X an = am+n
75 + 3x = 720
If the bases are equal, then the powers should also be equal.
⇒ 5 + 3x = 20
⇒ 5 + 3x – 5 = 20 – 5
⇒ 3x = 15
⇒ \(\frac{3 x}{3}=\frac{15}{3}\) = 5
∴ x = 5
![]()
Question 6.
If 10y = 10000 then 5y =?
Answer:
Given, 10y = 10000
10y = 10 × 10 × 10 × 10
10y = 104
If the bases are equal, then the powers should also be equal.
⇒ y = 4
Multiply by 5 on bothsides,
5 × y = 5 × 4
∴ 5y = 20
Question 7.
If 5x = 100 then find the following values.
(i) 5x+y
Answer:
Given 5x+y = 100
5x = 102
Multiply by 52
5x × 52 = 100 × 52
5x+2 = 100 × 25 (∵ am × an = am+n)
∴ 5x+2 = 2500
(ii) 5x-2
Answer:
Given 5x = 100
5x = 102
Divide by 52 on both sides
5x ÷ 52 = 100 ÷ 52
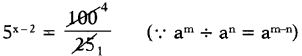
∴ 5x-2 = 4
Question 8.
By what number should 34 be multiplied so that the product is 243?
Answer:
Given number is 34
If we multiply 34 by ‘a’ the product is 243.
i.e. 34 × a = 243
= 3 × 3 × 3 × 3 × 3
34 × a = 35
Divide by 34 on both sides

If we multiply 34 by 3 we get 243.
Question 9.
Arushi computed (52)4 as 516 Has she done it correctly or not’? Justify your answer.
Answer:
Given, (52)4
We know) (am)n = am.n
= 52×4 = 58
∴ (52)4 = 58
But Arushi got 516 So, (52)4 ≠ 516
Therefore Arushi did wrong.
![]()
Question 10.
Is 35 × 45 equal to 1225? If not why? Justify your answer.
Answer:
Given, 35 × 45
We know am × bm = (a × b)m
So, 35 × 45 = 12 but not 125×5
= (3 × 4)5
= (12)5
35 × 45= 125
But given 35 × 45 = 1225.
So, this is wrong.
So, 35 × 45 ≠ 1225