SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion Ex 7.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion Ex 7.3
Question 1.
Find out whether the given quantities vary directly or inversely.
(i) Time taken to cover a distance, speed.
Answer:
Inversely proportional.
(ii) Area of land and its cost.
Answer:
Direct proportion.
(iii) Number of men for work, time taken to complete the work.
Answer:
Inverselv proportional.
(iv) Number of people, quantity of food grains each one gets (total quantity remains same).
Answer:
Inversely proportional.
(v) The length of a journey by bus and price of the ticket.
Answer:
Direct proportion.
![]()
Question 2.
If 24 men can construct a wall in. 10 days. In how many days will 15 men do it?
Answer:
If the number of men decreases working days will increase in the same proportion.
So, number of men and the working days are in inverse proportion.
Let the number of days to complete the work be ’x.
| Number of mens | Number of days |
| 24 | 10 |
| 15 | x |
By taking inverse proportion,
24 : 15 = x : 10
Then, product of means = Product of the extremes
⇒ 15 × x = 24 × 10
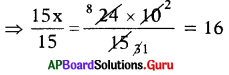
⇒ x = 16
∴ 15 men will complete the wall in 16 days.
Question 3.
In a hostel there are food provisions for 50 girls for 40 days. If 30 more girls join the hostel, how long will the provisions last?
Answer:
If the number of girls increases, then number of days will decrease in the same proportion.
So, number of girls and the days for food provisions lost are in inverse proportion.
Let the number of food provisions days be ’x’.
| Number of girls | Number of days |
| 50 | 40 |
| 50 + 30 = 80 | x |
By taking inverse proportion,
50 : 80 = x : 40
Then, product of means = Product of extremes
⇒ 80 × x = 50 × 40
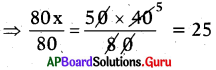
⇒ x = 25
∴ Number of days required to com-plete the food provisions for 80 girls is 25 days.
Question 4.
Suman travels a distance for 5 hours with a speed of 48 kilometres per hour. If he wants to travel the same in 4 hours at what speed he should travel?
Answer:
If the time decreases, then the speed will increase in the same proportion. Let the speed to cover the distance in 4 hours is ’x’.
| Time | Speed (kmph) |
| 5 | 48 |
| 4 | x |
By taking inverse proportion,
5 : 4 = x : 48
Then, Product of means = Product of extremes
⇒ 4 × x = 48 × 5
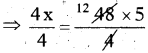
⇒ x = 60 kmph.
∴ Distance covered in 4 hours with the speed of 60 kmph.
Question 5.
A person has money to buy 8 bicycles of worth ₹ 4500 each. If the cost of the bicycle is decreased by ₹ 500, then how many bicycles cap he buy with the amount he has?

Answer:
If the cost of the bicyble decreases, then the number of cycles will increase in the same proportion.
Let the number of bicycles he can buy each with ₹ 4000 (4500 – 500) be ‘x’.
| Cost of the bicycle | Number of bicycles |
| 4500 | 8 |
| (4500-500) = 4000 | x |
By taking inverse proportion,
4500 : 4000 = x : 8
Then, Product of means = Product of extremes
⇒ 4000 × x = 4500 × 8
⇒ \(\frac{4000 x}{4000}=\frac{4500 \times 8}{4000}\) = 9
⇒ x = 9
∴ Number of bicycles bought with the same amount is 9.
![]()
Question 6.
2 pumps are required to fill a tank in 1 hour. How many pumps of the same type are used to fill the tank in 24 minutes?
Answer:
If the filling time decreases, then the number of pumps will increase in the same proportion.
Let the number of pumps to fill the tank be x.
| Time taken to fill the tank | Number of Pumps |
| 1 hour (60 minutes) | 2 |
| 24 minutes | x |
By taking inverse proportion,
60 : 24 = x : 2
Then, Product of means = Product of extremes
⇒ 24 × x = 60 × 2
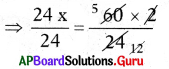
⇒ x = 5
∴ Number of pumps required to fill the tank in 24 minutes is 5.
Question 7.
18 men can reap a field in 10 days. For reaping the same field in 6 days, how many more men are required?

Answer:
If the reaping days decreases, then the number of men increases in the same proportion.
Let the number of men required to reap the field in 6 days is x.
| Number of mens | Number of reaping days |
| 18 | 10 |
| x | 6 |
By taking inverse proportion, 18 : x = 6 : 10
Then, Product of means = Product of extremes
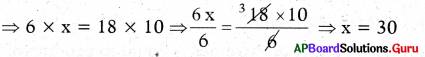
∴ Number of men required to reap the field in 6 days = 30
Number of more men = 30 – 18 = 12
Therefore 12 more men required to reap the field in 6 days.
![]()
Question 8.
1200 soldiers in a checkpost had enough food for 28 days. After 4 days some soldiers were transferred to another checkpost and thus remaining food is sufficient for 32 more days. How many soldiers left the checkpost?

Answer:
If the number of soldiers decreases, then the number of days food lost will increases in the same proportion.
Let the number of soldiers after transfer is x.
After 4 days,
| Number of Soldiers | Enough Food days |
| 1200 | 28 – 4 = 24 |
| x | 32 |
By taking inverse proportion, 1200 : x = 32 : 24
Then, Product of means = Product of extremes
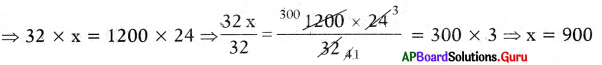
∴ Number of Soldiers remained in the checkpost = 900
Number of Soldiers transferred = 1200 – 900 = 300
So, 300 soldiers left the checkpost.