SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం Exercise 7.3
ప్రశ్న1.
ఈ క్రింద ఇవ్వబడిన రాశులు అనులోమానుపాతంలో ఉంటాయో, లేదా విలోమానుపాతంలో ఉంటాయో కనుక్కోండి:
(i) నిర్దిష్ట దూరాన్ని చేరుటకు పట్టు సమయం, వేగం.
సాధన :
విలోమానుపాతంలో ఉంటాయి.
(ii) స్థలం వైశాల్యం, దాని ఖరీదు.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.
(iii) పనిని పూర్తి చేయుటకు మనుషుల సంఖ్య, పని పూర్తవడానికి పట్టు సమయం.
సాధన :
విలోమానుపాతంలో ఉంటాయి.
(iv) మనుషుల సంఖ్య, ఒక్కొక్కరికి వచ్చే ఆహారధాన్యాల పరిమాణం (మొత్తం ఆహార ధాన్యాలు స్థిరం).
సాధన :
విలోమానుపాతంలో ఉంటాయి.
(v) బస్సులో ప్రయాణం చేసే దూరం, టికెట్ ధర.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.
![]()
ప్రశ్న2.
24 మంది వ్యక్తులు ఒక గోడను 10 రోజులలో నిర్మించగలరు. అంతే పొడవైన గోడను 15 మంది వ్యక్తులు ఎన్ని రోజులలో నిర్మించగలరు ?
సాధన :
వ్యక్తుల సంఖ్య, గోడ నిర్మాణం పూర్తికావడానికి పట్టు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి. (మనుషుల సంఖ్య ↑, రోజుల సంఖ్య ↓)
24 మంది వ్యక్తులు ఒక గోడను నిర్మించుటకు పట్టు రోజులు = 10
15 మంది అంతే పొడవుగల గోడను నిర్మించుటకు పట్టు రోజులు = x అనుకొందాము.
| వ్యక్తుల సంఖ్య | గోడ నిర్మాణానికి పట్టు రోజులు |
| 24 | 10 |
| 15 | x |
24 : 15 = x : 10
మధ్యమముల లబ్దం = అంత్యముల లబ్దం
= 15 × x = 24 × 10

విలోమానుపాతంలో కలవు కావున లబ్దం ఎల్లప్పుడు స్థిరం.
24 × 10 = 15 × x
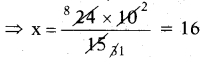
= 16 . 151
∴ x = 16
∴ 15 మంది వ్యక్తులు ఆ గోడను 16 రోజులలో నిర్మించగలరు.
ప్రశ్న3.
ఒక బాలికల వసతి గృహంలో, 50 మంది బాలికలకు 40 రోజులకు సరిపోయే ఆహార పదార్థాలు ఉన్నాయి. అదనంగా 30 మంది బాలికలు ప్రవేశం పొందిన, అందరికీ ఎన్ని రోజుల వరకూ ఆ ఆహార పదార్థాలు
సరిపోతాయి ?
సాధన :
వసతి గృహంలో బాలికల సంఖ్య, వారికి ఆహారం సరిపడు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి.
50 మంది బాలికలకు ఆహారం సరిపడు రోజులు = 40 అదనంగా 30 మంది బాలికలు ప్రవేశం పొందినచో వసతి గృహంలో 50 + 30 = 80 మంది బాలికలు ఉంటారు.
80 మంది బాలికలకు ఆహారం సరిపడు రోజులు = x అనుకొందాము.
| బాలికల సంఖ్య | ఆహారం సరిపడు రోజులు |
| 50 | 40 |
| 80 | x |
50 : 80 = x : 40
మధ్యమముల లబ్దం = అంత్యముల లబ్దం
⇒ 80 × x = 50 × 40

(లేదా)
విలోమానుపాతంలో ఉంటే లబ్ధం ఎల్లప్పుడు స్థిరము.
⇒ 50 × 40 = 80 × x

వసతి గృహంలోని 80 బాలికలకు 25 రోజుల వరకు ఆహార పదార్థాలు సరిపోతాయి.
ప్రశ్న4.
సుమన్ కొంత దూరం గంటకు 48 కి.మీ. సరాసరి వేగంతో, ఐదు గంటలపాటు ప్రయాణించాడు. అదే దూరాన్ని అతను నాలుగు గంటలలో ప్రయాణం చేయవలెనన్న, ఎంత వేగంతో ప్రయాణం చేయాలి ?
సాధన :
స్థిర దూరాన్ని ప్రయాణించుటకు వేగం, కాలం విలోమానుపాతంలో ఉంటాయి.
4 గంటలలో ఆ దూరాన్ని పూర్తి చేయుటకు అతని వేగం = x కి.మీ./గం. అనుకొనుము.
| వేగం | కాలం (kmph) |
| 48 | 5 |
| x | 4 |
48: x = 4 : 5
⇒ x × 4 = 48 × 5
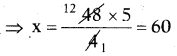
(లేదా)
విలోమానుపాతంలో ఉంటే లబ్దం ఎల్లప్పుడు స్థిరం.
48 × 5 = x × 4
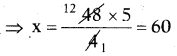
⇒ x = 60 కి.మీ./గం.
∴ 4 గంటల ప్రయాణంలో ఆ దూరాన్ని చేరుటకు సుమన్ గంటకు 60 కి.మీ. వేగంతో ప్రయాణం చేయాలి.
ప్రశ్న5.
ఒక్కొక్క సైకిలు వెల ₹ 4500 చొప్పున, ఎనిమిది సైకిళ్లను కొనుటకు ఒక వ్యక్తి వద్ద డబ్బులు ఉన్నవి. ఒక్కొక్క సైకిల్ వెల ₹500 తగ్గిన, తన వద్దవున్న అదే సొమ్ముతో అతను ఎన్ని సైకిళ్లను కొనగలడు ?

సాధన :
సైకిళ్ళ సంఖ్య మరియు వాని వెల విలోమానుపాతంలో ఉంటాయి.
₹4500 వెల నుండి ₹500 తగ్గినచో ఒక్కొక్క సైకిల్ వెల = 4500 – 500 = ₹4000
₹4000 వెలతో కొనగల సైకిళ్ళ సంఖ్య = X అను||
| ఒక్కొక్క సైకిల్ వెల | సైకిళ్ళ సంఖ్య |
| 4500 | 8 |
| 4000 | x |
4500: 4000 = x : 8
⇒ 4000 × x = 4500 × 8
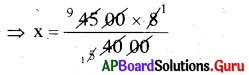
(లేదా)
4500 × 8 = 4000 × x
⇒ \(\frac{4500 \times 8}{4000}\) = x
⇒ 9 = x
∴ ఒక్కొక్క సైకిల్ వెల ₹500 తగ్గినచో అతను తన వద్ద గల సొమ్ముతో 9 సైకిళ్ళు కొనగలడు.
![]()
ప్రశ్న6.
2 పంపులు ఒక నీళ్ల ట్యాంకును, ఒక గంట సమయంలో నింపగలవు. అదే నీళ్ళ ట్యాంక్ ను 24 ని.లలో నింపవలెనన్న ఎన్ని పంపులు కావలెను ?
సాధన :
పంపుల సంఖ్య, ట్యాంకును నింపు సమయం విలోమానుపాతంలో ఉంటాయి.
24 నిమిషాలలో ట్యాంకును నింపుటకు అవసరమగు పంపులు = x అనుకొనుము.
| పంపుల సంఖ్య | నింపుటకు అవసరమగు కాలం |
| 2 | 60 ని॥ (1 గంట) |
| x | 24 ని|| |
2 : x = 24 : 60
⇒ 24 × x = 60 × 2
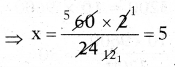
(లేదా)
2 × 60 = x × 24
⇒ \(\frac{2 \times 60}{24}\) = x
⇒ 5 = x
∴ నీళ్ళ ట్యాంకు 24 నిమిషాలలో నింపుటకు 5 పంపులు అవసరము.
ప్రశ్న7.
18 మంది వ్యక్తులు ఒక పొలంలో పంటను 10 రోజులలో కోయగలరు. అదే పంటను 15 రోజులలో కోయవలెనన్న, ఎంత మంది మనుషులు కావలెను ?

సాధన :
వ్యక్తుల సంఖ్య, పంటను కోయు రోజులు విలోమాను పాతంలో ఉంటాయి.
15 రోజులలో పంట కోయుటకు కావలసిన మనుషులు = x అనుకొందాము.
| మనుషుల సంఖ్య | పంట కోయు రోజులు |
| 18 | 10 |
| x | 15 |
18 : x = 15 : 10
⇒ 15 × x = 18 × 10
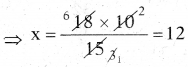
(లేదా)
⇒ 18 × 10 = x × 15
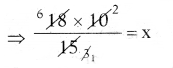
⇒ x = 12
∴ 15 రోజులలో పంట కోయుటకు 12 మంది మనుషులు కావలెను.
ప్రశ్న8.
ఒక సరిహద్దు చెక్ పోస్ట్ వద్ద 1200 మంది సైనికులకు 28 రోజులకు సరిపోయే ఆహార పదార్థాలు ఉన్నాయి. 4 రోజుల తర్వాత కొంతమంది సైనికులు వేరొక చెక్ పోస్టు బదిలీకాగా, మిగిలిన వారికి 32 రోజులకు ఆహార పదార్థాలు సరిపోయాయి. అయిన ఎంత మంది సైనికులు బదిలీ అయ్యారు ?

సాధన :
1200 మంది సైనికులకు ఆహారం సరిపోవు రోజులు = 28
4 రోజుల తరువాత 1200 మంది సైనికులకు ఆహారం – సరిపోవు రోజులు = 28 – 4 = 24
4 రోజుల తరువాత ‘x’ మంది సైనికులు బదిలీ అయినారు అనుకొందాము.
ఇప్పుడు సైన్యంలోని సైనికుల సంఖ్య 1200 – x.
వీరికి ఆహారం సరిపోవు రోజులు = 32
సైనికుల సంఖ్య, వారికి ఆహారం సరిపోవు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి.
| సైనికుల సంఖ్య | ఆహారం సరిపోవు రోజులు |
| 1200 | 24 |
| 1200 – x | 32 |
1200 : 1200 – x = 32 : 24
(1200 – x) 32 = 1200 × 24

⇒ 1200 – x = 900
⇒ 1200 – 900 = x
∴ 300 = X
(లేదా)
1200 × 24 = (1200 – x)32
⇒ \(\frac{1200 \times 24}{32}\) = 1200 – x
⇒ 900 = 1200 – x
⇒ x = 1200 – 900
⇒ x = 300
∴ బదిలీ అయిన సైనికుల సంఖ్య = 300