SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion Ex 7.2 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion Ex 7.2
Question 1.
Find out whether the given quantities are in direct proportion or not.
(i) Cost of pens, number of pens.
Answer:
Direct proportion. (As the number of pens increases, their total cost also increases)
(ii) Number of people, food required to them.
Answer:
Direct proportion. (As the number of people increases, food required for them also increases)
(iii) Speed of a car, time taken to reach destination.
Answer:
Not in direct proportion. (As the speed increases, time taken by the car reduces)
(iv) Time taken, distance covered.
Answer:
Direct proportion. (As the time increases, distance covered will be increased)
(v) Cost of the vegetables, number of vegetable bags.
Answer:
There is no relation between cost of vegetables and number of vegetable bags.
![]()
Question 2.
Five people went to a Park and paid ₹ 580 for tickets. If three people went to the Park, how much money did they have to pay?

Answer:
We know that if the number of people decreases the amount of the tickets also decreases such that the ratio of number of people and the ratio of their tickets amount will remain the same. That means here number of people and the amount of their tickets are in proportion.
Amount paid for tickets by 5 people = ₹ 580
Let the amount paid for tickets by 3 people be x.
Then, 5 : 3 = 580 : x
If the ratios are equal, the product of means = the product of the extremes.
⇒ 5 × x = 3 × 580
⇒ \(\frac{5 x}{5}=\frac{3 \times 580}{5}\)
⇒ x = 3 × 116
⇒ x = 348
∴ Money paid by three persons for tickets = ₹ 348.
Question 3.
A map drawn with a scale of 1 cm re-presents 26 km. If the original distance between two stations 1404 km., then what would be the distance between the stations in the map?
Answer:
We know that if the distance in the map increases the original distance also increases such that the ratio of distance in the map end ratio of their original distance will remain the same. That means here the distance in map and original distance are in proportion.
Distance 26 km scale represented in the map = 1 cm.
Let the distance 1404 km in the map be equal to x cm.
Then, 26 : 1404 = 1 : x
If the ratio are equal, the product of means = the product of the extremes
⇒ 26 × x = 1404 × 1
⇒ \(\frac{26 x}{26}=\frac{1404}{26}\)
⇒ x = 54 cm
∴ Distance 1404 km between the stations in the map = 54 cm.
![]()
Question 4.
The weight of 72 pipes is 180 kg. Then what is the weight of 90 such pipes?

Answer:
We know that if the number of pipes increases their weight also increases, such that the ratio of number of pipes and the ratio of their weights will remain the same. That means here number of pipes and their weights are in proportion.
Given weight of 72 pipes 180 kg
Let the weight of 90 pipes = x kg ,
Then 72 : 90 = 180 : x
If the ratios are equal, the product of means = The product of extremes
⇒ 72 × x = 90 × 180
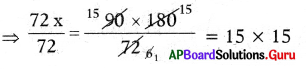
⇒ x = 225 kg
∴ weight of 90 pipes = 225 kg
Question 5.
A motorbike requires 3 liters of petrol to cover 135 km. on average. How many litres of petrol will be required to cover 495km?
Answer:
We know that if the distance increases quantity of petrol also increases, such that the ratio of distances and the ratio of the required quantity of petrol will remain the same. That means here distance and required quantity of petrol are in proportion.
Given quantity of petrol required to cover 135 km = 3l
Let the quantity of petrol required to cover 495 km = xl
Then 135 : 495 = 3 : x
If the ratios are equal, the product of means = The product of the extremes
⇒ 135 × x = 495 × 3

⇒ x = 11 l
∴ The quantity of petrol required to cover 495 km = 11 l.
![]()
Question 6.
The shadow of a pole with the height of 10 m. is 6 m. Then find the height of another pole whose shadow is 9 m. at the same time.
Answer:
We know that if the length of shadow increases the height of the pole also increases, such that the ratio of lengths of shadows and the ratio of heights of poles will remain the same.
That means here lengths of shadows and heights of poles are in proportion.
Given height of the pole when its shadow’s length is 6 m = 10 m
Let the height of the pole when its shadow’s length is 9 m = x m
Then 6 : 9 = 10 : x If the ratios are equal,
The product of means = The product of the extremes
⇒ 6 × x = 9 × 10
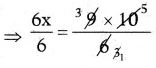
⇒ x = 3 × 5 = 15m
∴ The height of the pole when its shadows length is 9 m = 15 m.