AP State Syllabus AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangle and Its Properties InText Questions
![]()
Try This
Question 1.
The lengths of two sides of a triangle are 6 cm and 9 cpi. Write all the possible lengths of the third side. (Page No. 92)
Solution:
The possible length of the third side must greater than (9— 6) and less than (9 + 6).
∴ The third side may be 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, 9 cm, 10 cm, 11 cm, 12 cm, 13 cm, 14 cm.
![]()
Try This
Question 1.
Uma felt that a triangle can be formed with three collinear points. Do you agree ? Why? Draw diagrams to justify your answer. (Page No. 88)
Solution:
Uma ¡s not correct.
A triangle cant be formed with three collinear points.

Do This
Question 1.
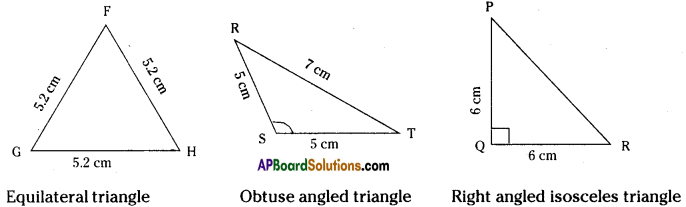
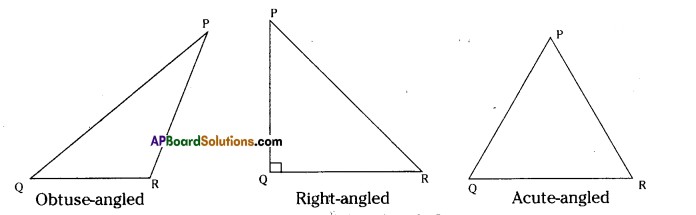
Classify the following triangles according to their (i) sides and (ii) angles. (Page No. 89)
Solution:
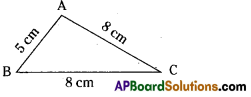
Two sides AC and BC are equal.
∴ ∆ABC is an isosceles triangle
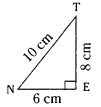
As ∠E = 90°;
∆NET is a right angled triangle.
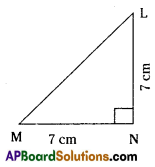
In ∆MNL,
MN = NL and ∠N = 90°
∆ MNL is right angled isosceless triangle.
![]()
Question 2.
Write the six elements (i.e., the 3 sides and 3 angles) of ∆ABC.
Solution:
The three sides \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\) and the three angles ∠A, ∠B and ∠C are the six elements of ∆ABC.
Question 3.
Write the side opposite to vertex Q in ∆PQR.
Solution:
The side opposite to the vertex Q is \(\text { PR }\) .
Question 4.
Write the angle opposite to side \(\text { LM }\) in ∆LMN.
Solution:
Angle opposite to side \(\text { LM }\) is ∠N.
Question 5.
Write the vertex opposite to side \(\text { RT }\) in ∆RST.
Solution:
Vertex opposite to \(\text { RT }\) is S.
Try This
Question 1.
Rashmi claims that no triangle can have more than one right angle. Do you agree with her. Why ?
Solution:
Yes, Rashmi is correct. A triangle can’t have more than one right angle. As the sum of two right angles is 180° there will be no scope for 3rd angle.
![]()
Question 2.
Kamal claims that no triangle can have more than two acute angles. Do you agree with him. Why?
Solution:
No. Kamal is not right. A triangle can have all the three acute angles.
(60°, 60°, 60°), (30°, 70°, 80°), (40°, 60°, 80°) etc ………….
Question 3 i)
Draw altitudes from P to \(\text { QR }\) for the following triangles. Also, draw altitudes from the other vertices.
ii) Will an altitude always lie in the interior of a triangle ?
iii) Can you think of a triangle in which the two altitudes of a triangle are two of its sides ?
Solution:
i)
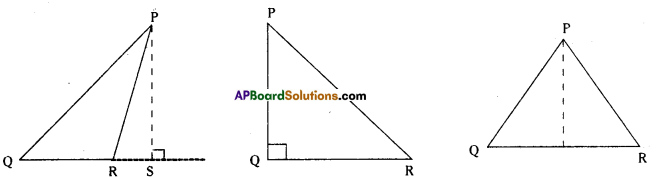
ii) An altitude need not necessarily be in the Interior of a triangle.
iii) Yes. In a right triangle the two sides containing the right angle are the two altitudes of it.
Do This
Question 1.
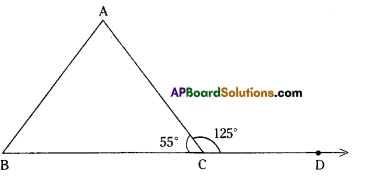
Draw ∆ABC and fofm an exterior ∠ACD. Now take a protractor and measure ∠ACD, ∠A and ∠B. Find the sum ∠A + ∠B and compare it with the measure ∠ACD. Do you observe that ZACD is equal (or nearly equal) to ∠A + ∠B ? (Page No. 102)
Solution:
For instance in the adjacent figure
∠A = 68° ; ∠B = 57°
∠A + ∠B = 68° + 57° = 125 ∠ACD = 125°
∴ ∠ACD = ∠A + ∠B
![]()
Question 2.
Copy each of the following triangles. In each case verify that an exterior angle of a triangle^ is equal to the sum of the two interior opposite angles. (Page No. 103)
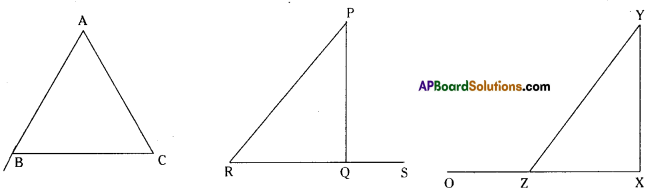
Solution:
From the figures
exterior ∠B = ∠A + ∠C
∠130° = 65° + 65°
∠PQS = ∠P + ∠R also ∠YZO = ∠X
90° = 40° + 50° 120° = 90° + 30°