SCERT AP 7th Class Maths Solutions Pdf Chapter 5 Triangles Ex 5.2 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangles Exercise 5.2
Question 1.
Which of the following angles form a triangle?
(a) 60°, 70°, 80°
Answer:
Given angles are 60°, 70°, 80°.
Sum of the angles = 60° + 70° + 80°
= 210° >180°
So, 60°, 70°, 80° cannot form a triangle.
(b) 65°, 45°, 70°
Answer:
Given angles are 65°, 45°, 70°.
Sum of the angles = 65° + 45° + 70° = 180°
So, 65°, 45°, 70° can form.a triangle.
(c) 40°, 50°, 60°
Answer:
Given angles are 40°, 50°, 60°
Sum of the angles = 40° + 50° + 60°
= 150° <180°
So, 40°, 50°, 60° cannot form a triangle.
(d) 60°, 30°, 90°
Answer:
Given angles are 60°, 30°, 90°.
Sum of the angles = 60° + 30° + 90° = 180°
So, 60°, 30°, 90° can form a triangle.
(e) 38°, 102°, 40°
Answer:
Given angles are 38°, 102°, 40°
Sum of the angles = 38° + 102° + 40° = 180°
So, 38°, 102°, 40° can form a triangle.
(f) 100°, 30°, 45°
Sol. Given angles are 100°, 30°, 45°
Sum of the angles = 100° + 30° + 45° = 175° < 180°
So, 100°, 30°, 45° cannot form a triangle.
![]()
Question 2.
Sum of two interior angles of a triangle is 105°. Find the third angle.
Answer:
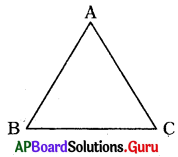
In ∆ABC given sum of two angles is 105°.
Let ∠A + ∠B = 105°
We know that in ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ 105° + ∠C = 180°
⇒ 105° + ∠C – 105° – 180° – 105°
⇒ ∠C = 75°
∴ Third angle is 75°.
Question 3.
In ∆PQR, if ∠P=65° and ∠Q = 50°, then find ∠R.
Answer:
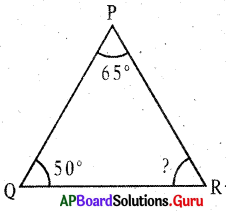
Given in ∆PQR, ∠P = 65°, ∠Q = 50°
We know that in ∆PQR,.
∠P + ∠Q + ∠R = 180°
⇒ 65° + 50° + ∠R =180°
⇒ 115° + ∠R = 180°
⇒ 115° + ∠R – 115°
⇒ 180° – 115°
⇒∠R = 65°
∴ ∠R = 65°
Question 4.
Find the missing angles in each of the following triangles.
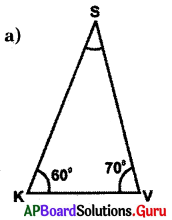
Answer:
Given in ∆SKV, ∠K = 60°, ∠V = 70°
We know that in ∆SKV,
∠S + ∠K + ∠V = 180°
⇒ ∠S + 60° + 70° = 180°
⇒ ∠S + 130° = 180°
⇒∠S + 130°- 130° = 180°- 130°
⇒ ∠S = 50°
∴ ∠S = 50°
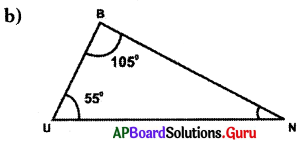
Answer:
Given in ∆BUN, ∠B = 105°, ∠U – 55°
We know that in ABUN,
∠B + ∠U + ∠N = 180°
⇒ 105° + 55° + ∠N = 180°
⇒ 160° + ∠N = 180°
⇒ 160° + ∠N – 160° = 180° – 160°
∴ ∠N = 20°
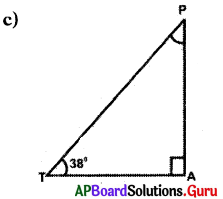
Answer:
Given in ∆PAT, ∠A = 90°, ∠T = 38°
We know that in ∆PAT,
∠P + ∠A + ∠T = 180°
⇒ ∠P + 90° + 38° = 180°
⇒ ∠P + 128° = 180°
⇒ ∠P + 128°- 128° = 180° – 128°
∴ ∠P = 52°
![]()
Question 5.
Find the value of ‘x’ in each of the given triangles.
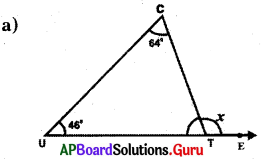
Answer:
In ∆CUT, ∠C = 64°, ∠U = 46° and exterior angle ∠CTE = x =?
∠C + ∠U + ∠T= 180°
⇒ 64° + 46° + ∠T = 180°
⇒ 110° + ∠T= 180°
⇒ 110° + ∠T – 110° = 180°- 110°
∠UTC = ∠T = 70°
∠UTC + ∠CTE = 180° (linear pair of angles)
⇒ 70° + x° = 180°
⇒ 70° + x° – 70° = 180°-70°
∴ x = 110°
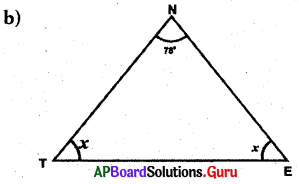
Answer:
In ∆NTE, ∠N = 78°, ∠T = x, ∠E = x,
We know that in ANTE, ‘
∠N + ∠T + ∠E = 180°
⇒ 78° + x + x = 180°
⇒ 78° + 2x – 78° = 180° – 78°
⇒ 2x = 102°
⇒ \(\frac{2 x}{2}=\frac{102^{\circ}}{2}\)
∴ x = 51°
Question 6.
Find the value of ‘x’ and ‘y’ in each of the following triangles.
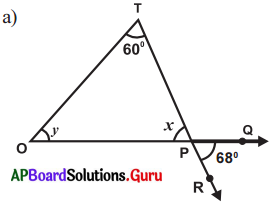
Answer:
In ∆TOP given ∠T = 6O, ∠O = y°
∠OPT = x° and ∠RPQ = 68°
∠OFT = ∠RPQ (Vertically, opposite angles are equal)
x = 68°
We know that in ∆TOP
∠T + ∠O + ∠P= 1800
⇒ 60° + y° + x° = 180°
⇒ 60° + y° + 68° = 180°
⇒ 128° + y – 128° = 180°- 128°
∴ y = 52° ‘
∴ x = 68°and y = 52°
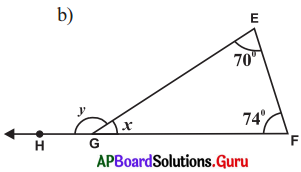
Answer:
In ∆EFG, ∠E = 70°, ∠F = 74° and ∠EGF – x° and∠EGH = y°
We know that in ∆EFG,
∠E + ∠F + ∠G = 180°
⇒ 70° + 74° + ∠EGF – 180°
⇒ 144° + x – 144° = 180° – 144°
⇒ x = 36°
∴ ∠EGF .= 36°
∠EGF + ∠EGH = 180° (linear pair of angles)
⇒ 36° + ∠EGH = 180°
⇒ 36° + y° – 36° = 180° – 36°
∴ y = 144°
∴ x = 36° and y = 144°
Question 7.
In a right angled triangle one acute angle is 37°. Find the other acute angle.
Answer:
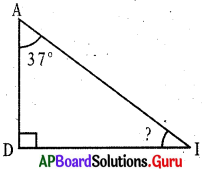
Given in ∆ADI, ∠A = 37°, ∠D = 90°, ∠I =?
We know that in ∆ADI.
∠A + ∠D + ∠I = 180°
⇒ 37° + 90° + ∠I = 180°
⇒ 127° + ∠I – 127° = 180°- 127°
∴ ∠I – 53°
∴ Other acute angle is 53°.
![]()
Question 8.
If the three angles of a triangular sign-board are 2x°, (x – 10)° and (x + 30)° respectively. Then find it’s angles.
Answer:
Given the three angles of a triangular signboard are 2x°, (x – 10)° and (x +30)°.
We know that in a triangle,
2x + (x – 10) + (x + 30) = 180°
⇒ 2x + x- 10° + x + 30 = 180°
⇒ 4x + 20 = 180°
⇒ 4x + 20 – 20 = 180° – 20°
⇒ 4x = 160°
⇒ \(\frac{4 x}{4}=\frac{160^{\circ}}{4}\)
∴ x = 40°
Angles are 2x°, (x- 10)°, (x + 30)° 2(40°), 40° – 10, 40 + 30
Angles of signboard are : 80°, 30°, 70°.
Question 9.
If one angle of a triangle is 80°, find the other two angles which are equal.
Answer:
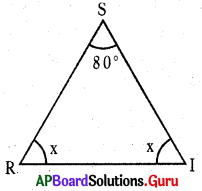
Given one angle of a triangle is 80°,
In ∆SRI, ZS = 80° and ∠R = ∠I = x
We know that in ∆SRI,
∠S + ∠R + ∠I = 180°
⇒ 80° + x + x = 180°
⇒ 80° + 2x-80° = 180°-80°
⇒ 2x = 100°
⇒ \(\frac{2 x}{2}=\frac{100^{\circ}}{2}\)
∴ x = 50°
Therefore angles of triangle are 80°, 50° and 50°.
Question 10.
State TRUE or FALSE for each of the following statements and write the reasons for the FALSE statement.
(i) A triangle can have two right angles.
Answer:
FALSE.
In triangle sum of three angles is 180°. In triangle, if two angles are two right angles (90° + 90° = 180°).
Then, sum of three angles is greater than 180°.
(ii) A triangle can have two acute angles.
Answer:
TRUE.
(iii) A triangle can have two obtuse angles.
Answer:
FALSE.
In triangle sum of three angles is 180°. In traingle, if two angles are two obtuse angles, then sum of three angles is greater than 180°.
![]()
Question 11.
The angles of a triangle are in the ratio 2 : 4 : 3, then find the angles.
Answer:
Given the ratio of the angles of a ’ triangle are 2 : 4 : 3.
2x : 4x : 3x
Sum of the angles of a triangle is 180°.
⇒ 2x + 4x + 3x = 180°
⇒ 9x = 180°
⇒ \(\frac{9 x}{9}=\frac{180^{\circ}}{9}\)
∴ x = 20°
Angles are ⇒ 2x : 4x :,3x
2(20°) : 4(20°): 3(20°)
40°: 80° : 60°
∴ Angles of a triangle are 40°, 80°, 60°.