SCERT AP 7th Class Maths Solutions Pdf Chapter 4 Lines and Angles InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles InText Questions
Check Your Progress [Page No. 66]
Question 1.
Find the complementary angles of
(i) 27°
Answer:
If the sum of any two angles is 90°, then the angles are called as complementary angles.
Complementary angle of 27° is
(90 – 27) = 63°
(ii) 43°
Answer:
Complementary angle of 43° is
(90 – 43) = 47°
(iii) k°
Answer:
Complementary angle of k° is (90 – k)°
(iv) 2°
Answer:
Complementary angle of 2° is
(90 – 2) = 88°
![]()
Question 2.
Find the supplementary angles of
(i) 13°
Answer:
If the sum of any two angles is 180°, then the angles are called as supplementary angles.
Supplementary angle of 13° is
(180 – 13) = 167°
(ii) 97°
Answer:
Supplementary angle of 97° is
(180 – 97) = 83°
(iii) a°
Answer:
Supplementary angle of a° is
(180 – a)°
(iv) 46°
Answer:
Supplementary angle of 46° is
(180 – 46) = 134°
Question 3.
Find the conjugate angles of
(i) 74°
Answer:
If the sum of any two angles is 360°, then the angles are called as conjugate angles.
Conjugate angle of 74° is
(360 – 74) = 286°
(ii) 180°
Answer:
Conjugate angle of 180° is
(360- 180) = 180°
(iii) m°
Answer:
Conjugate angle of m° is (360 – m)°
(iv) 300°
Answer:
Conjugate angle of 300° is
(360.-300) = 60°
[Page No. 66]
Question 1.
Umesh said, “Two acute angles cannot form a pair of supplementary angles.” Do you agree ? Give reason.
Answer:
Yes, acute angle is always less than 90°. So, sum of two acute angles is always less than 180°.
Therefore, two acute angles cannot form a pair of supplementary angles (180°).
Question 2.
Lokesh said, “Each angle in any pair of complementary angles is always acute.” Do you agree? Justify your answer.
Answer:
Yes, sum of any two acute angles is 90°, then they are complementary angles. If they are not acute means they may . be right angle (90°) or obtuse angle (> 90°) or etc.
So, its impossible.
Therefore, each angle in any pair of complementary angles is always acute.
Let’s Think [Page No. 69]
Question 1.
In the figure, ∠AOB and ∠BPC are not adjacent angles. Why? Give reason.
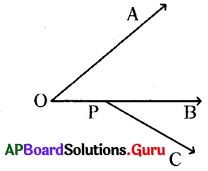
Answer:
In the given figure, ∠AOB and ∠BPC are not adjacent angles. Because, they have no common vertex and no common arm.
![]()
Question 2.
In the figure, ∠AOB and ∠COD have common vertex O. But ∠AOB, ∠COD are not adjacent angles. Why? Give reason.
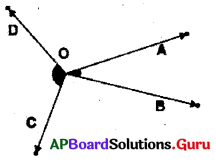
Answer:
In the given figure, ∠AOB and ∠COD are not adjacent angles. Because, they have common vertex. But they have no common arm.
Question 3.
In the figure, ∠POQ and ∠POR have common vertex O and common arm OP but ∠POQ and ∠POR are not adjacent angles. Why? Give reason.
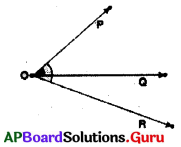
Answer:
∠POQ and ∠POR have common vertex O and common arm OP. But they are not lie either side of the common arm. That’s why they are not adjacent angles.
Check Your Progress [Page No. 70]
Question 1.
In the adjacent figure \(\overrightarrow{\mathbf{P R}}\) is a straight line and O is a point on the line. \(\overrightarrow{\mathbf{O Q}}\) is a ray.
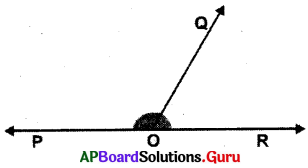
(i) If ∠QOR= 50°, then what is ∠POQ?
Answer:
Given ∠QOR= 50°
∠POQ, ∠QOR are linear pair.
⇒ ∠POQ + ∠QOR = 180°
⇒ ∠POQ + 50° = 180°
⇒ ∠POQ — 180° – 50° = 130°
.-. ∠POQ =130°
(ii) If ∠QOP = 102°, then what is ∠QOR?
. Sol. Given ∠QOP = 102°
∠QOP and ∠QOR are linear pair.
⇒ ∠QOP + ∠QOR = 180°
⇒ 102° + ∠QOR = 180°
⇒ 102°- 102° + ∠QOR = 180°- 102°
⇒ ∠QOR = 78°
Let’s Explore [Page No. 70]
Question 1.
A linear pair of angles must be adja-cent but adjacent angles need not be linear pair. Do you agree? Draw a figure to support your answer.
Answer:
Yes.
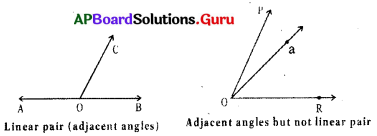
Question 2.
Mahesh said that the sum of two angles 30° and 150° is 180°, hence they are linear pair. Do you agree? Justify your answer.
Answer:
No, sum of two angles is 180°, then they are said to be supplementary angles.
If the two angles are on the same straight line and they are adjacent they are said to be linear pair.
So, the two angles 30° and 150° are need not be linear pair.
![]()
Let’s Think [Page No. 70]
Question 1.
In the adjacent figure, AB is a straight line, O is a point on AB. OC is a ray. Take a point D in the interior of ∠AOC, join OD.
Find ∠AOD + ∠DOC + ∠COB.
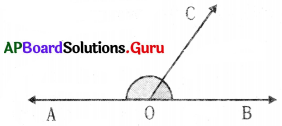
Answer:
Given ∠AOC and ∠COB are linear pair. But ∠AOC = ∠AOD + ∠DOC
⇒ ∠AOC + ∠COB = 180° (linear pair)
⇒ ∠AOD + ∠DOC + ZCOB = 180°
Question 2.
In the given figure, AG is a straight line. Find the value of ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6.
Answer:
Given ∠AOC and ∠COG are linear pair. ∠AOC + ∠COG = 180° (linear pair)
But ∠AOC = ∠AOB + ∠BOC
= ∠1 + ∠2
∠COG – ∠COD + ∠DOE + ∠EOF + ∠FOG – ∠3 + ∠4 + ∠5 + ∠6
=> (∠AOB + ∠BOC) + (∠COD + ∠DOE + ∠EOF + ∠FOG)
= 180°
=> ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6
= 180°
Therefore, the sum of angles at a point on the same side of the line is 180°.
Let’s DO Activity [Page No. 72]
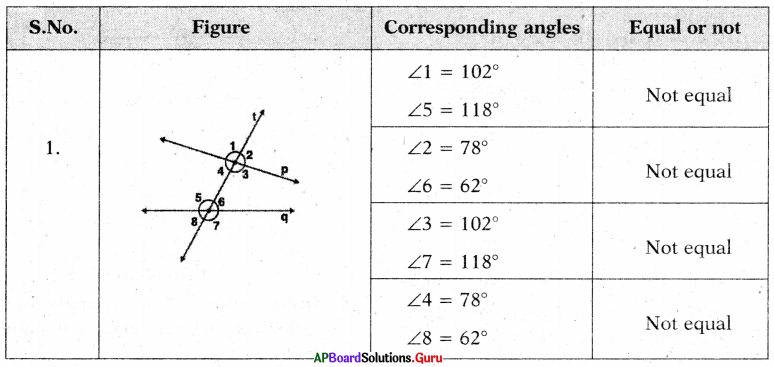
Take a white paper. Draw 3 distinct pairs of intersecting lines on this paper. Measure the angles so formed and fill the table.
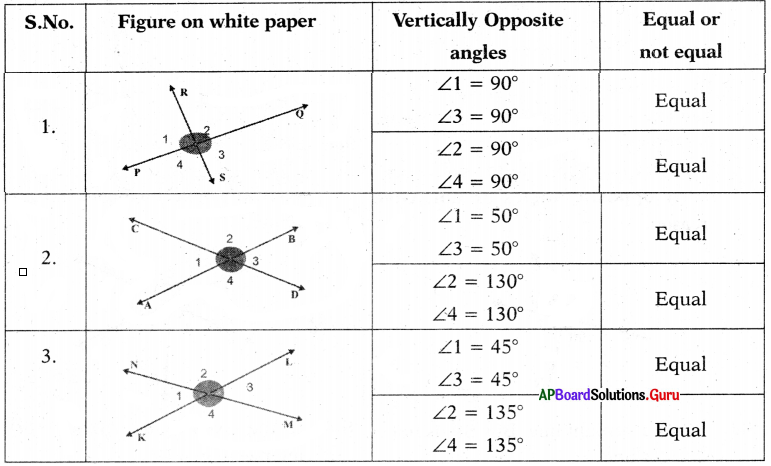
From the above table, we observe that “vertically opposite angles are equal.
Check Your Progress [Page No. 73]
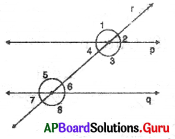
In the figure three lines p, q and r inter-sect at a point O. Observe the angles in the figure. Write answers to the following.
Question 1.
What is the vertically opposite angle to ∠1?
Answer:
Vertically opposite angle to ∠1 is ∠4.
Question 2.
What is the vertically opposite angle to ∠6?
Answer:
Vertically opposite angle to ∠6 is ∠3.
Question 3.
If ∠2 = 50°, then what is ∠5?
Answer:
Vertically opposite angle of ∠2 is ∠5. So, ∠5 = ∠2 = 50° ∠5 = 50°
Let’s Think [Page No. 75]
Question 1.
In the figure, the line l intersects other two lines m and n at A and B respectively. Hence l is a transversal. Is there
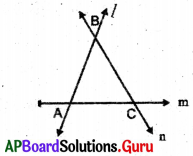
Give reason.
Answer:
Yes.
1) The line m intersects other two lines / and n at two distinct points A and C respectively. Hence m is a transversal line.
2) The line n intersects other two lines / and m at two distinct points B and C respectively. Hence n is a transversal line.
Question 2.
How many transversals can be drawn for the given pair of lines?
Answer:
One and only one transversal line can be drawn for the given pair of lines.
![]()
Check Your Progress [Page No. 76]
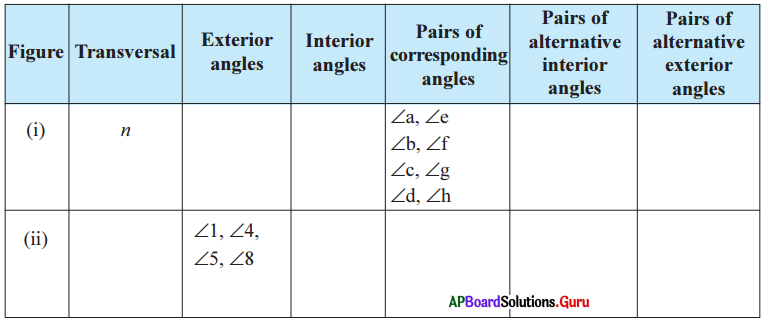
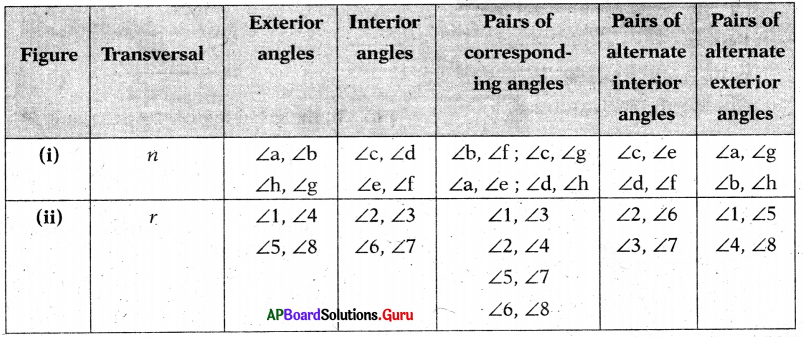
Observe the figures (i) and (ii) then fill the table.
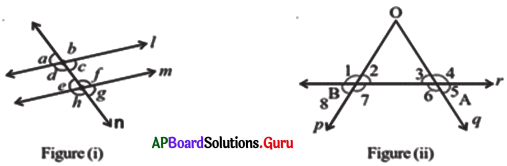

Answer:

Check Your Progress [Page No. 78]
In the figure, p ∥ q and t is a transversal. Observe the angles formed.
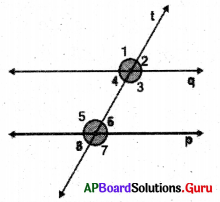
Question 1.
If ∠1 = 100°, then what is ∠5?
Answer:
In the given figure ∠5 = Z1 (corresponding angles)
Given ∠1 = 100°
So, ∠5 = ∠1 = 100°
∴ ∠5 – 100°
Question 2.
If ∠8 = 80°, then what is ∠4?
Answer:
In the given figure ∠4 = ∠8 (corresponding angles)
Given ∠8 = 80°
So, ∠4 — ∠8 = 80°
∴ ∠4 = 80°
Question 3.
If ∠3 = 145°, then what is ∠7?
Answer:
In the given figure ∠7 = ∠3 (corresponding angles)
Given ∠3 = 145°
So, ∠7 = ∠3 = 145°
∴ ∠7 – 145°
Question 4.
If ∠6 = 30°, then what is ∠2?
Answer:
In the given figure ∠2 = ∠6 (corresponding angles)
Given ∠6 = 30°
So, ∠2 = ∠6 = 30°
∴ ∠2 = 30°
Let’s Think [Page No. 78]
Question 1.
What is the relation between alternate exterior angles formed by a transversal on parallel lines?
Answer:
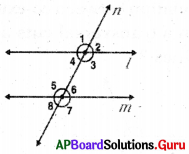
Alternate exterior angles are equal. That is ∠1 = ∠7 and ∠2 = ∠8
Check Your Progress [Page No. 80]
In the figure, m∥ n and l is a transversal.
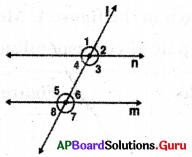
Question 1.
If ∠3 = 116°, then what is ∠5?
Answer:
In the figure ∠5 = ∠3 (Alternate interior angles)
Given ∠3 = 116°
So, ∠5 = ∠3 = 116°
∴ ∠5 = 116°
Question 2.
If ∠4 = 51°, then what is ∠5?
Answer:
In the figure the interior angles in the same side of transversal are supple-mentary’.
So, ∠5 + ∠4 = 180° we know ∠4 = 51°
∠5 + 51° = 180°
∠5 + 51° – 51° = 180° – 51°
=> ∠5 = 129°
Question 3.
If ∠1 = 123° then what is ∠7?
Answer:
In the given figure
∠7 = ∠1 (Alternative exterior angles) Given ∠1 = 123°
So, ∠7 = ∠1 = 123°
∴ ∠7 = 123° .
Question 4.
If ∠2 = 66° then what is ∠7?
Answer:
In the given figure,
sum of the exterior angles are the same side of transversal are supplementary. So, ∠2 + ∠7 = 180°
=> 66° + ∠7 = 180° (Given ∠2 = 66°)
=> 66° + ∠7 – 66° = 180° – 66°
=> ∠7 = 114°
∴ ∠7 = 114°
Let’s Think [Page No. 80]
Question 1.
What is the relation between co-exterior angles, when a transversal cuts a pair of parallel lines?
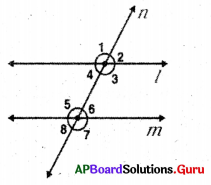
Answer:
Co-exterior angles are supplementary. That is ∠2 + ∠7 = 180° and ∠1 + ∠8 = 180°
![]()
Let’s Do Activity [Page N0. 80]
Take a white paper and draw a pair of non-parallel lines p and q and a transversal shown in the fIgure 1. Measure the corresponding angles and fill the table. Measure the pair óf corresponding angles and fill the table.
Check Your Progress [Page No. 81].
From the figure, state which property that is used in each of the following.
Question 1.
If ∠3 = ∠5, then p ∥ q.
Answer:
Given ∠3 = ∠5
Alternative interior angles are equal.
Question 2.
If ∠3 + ∠6 = 180°, then p ∥ q.
Answer:
Given ∠3 + ∠6 = 180°
Interior angles on the same Side of transversal are supplementary.
Question 3.
If ∠3 = ∠8, then p∥q.
Answer:
Given ∠3 = = ∠8 .
∠3 and ∠8 are not corresponding angles and not alternate interior angles.
So, ∠3 ≠ ∠8.
Let’s Explore [Page No. 81]
Question 1.
When a transversal intersects two lines and a pair of alternate exterior angles are equal, what can you say about the two lines?
Answer:
If a pair of alternate exterior angles are equal, then the two lines are parallel to each other.
Question 2.
When a transversal intersects two lines and a pair of co-exterior angles are supplementary, what can you say about the two-lines?
Answer:
If a pair of co-exterior angles are supplementary’ then the two lines are parallel to each other.
Examples:
Question 1.
In the given figure, ∠B and ∠E are complementary angles. Find the value of x.
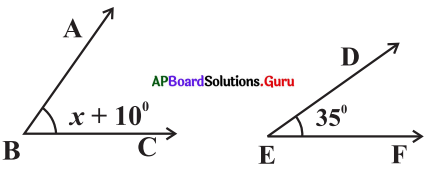
Answer:
From the figure,
∠B = x + 10°and ∠E =35°
Since ∠B and ∠E are complementary angles,
∠B + ∠E =90°
⇒ x + 10° + 35° = 90°
⇒ x + 45° = 90°
⇒ x = 90°- 45°
x = 45°
Question 2.
If the ratio of supplementary angles is 4 : 5, then find the two angles.
Answer:
Given ratio of supplementary angles = 4:5
Sum of the parts in the ratio = 4 + 5 = 9
Sum of the supplementary angles = 180°
First angle = \(\frac{4}{9}\) × 180° = 80°
Second angle = \(\frac{5}{9}\) × 180 °= 100°
![]()
Question 3.
Find the linear pair of angles which are equal to each other?
Answer:
Let the equal linear pair of angles are x° and x°.
⇒ x° + x° = 180° .
⇒ 2x° = 180°
⇒ x° = \(\frac{180^{\circ}}{2}\)
∴ x° = 90°
Hence, each angle = 90°
Question 4.
In the given figure, PS is a straight line, find x°.
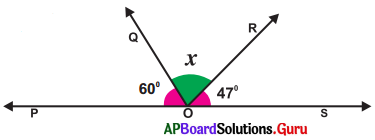
Answer:
From the given figure, ∠POQ = 60°
∠QOR = x°
∠ROS = 47°
But ∠POQ + ∠QOR + ∠ROS = 180°
⇒ 60° + x° + 47° = 180°
⇒ x° + 107° = 180°
⇒ x° = 180°- 107°
∴ x° = 73°
Question 5.
Observe the figure, then find x, y and z.
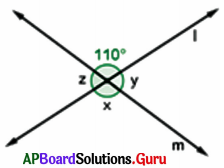
Answer:
From the figure, x = 110° (vertically opposite angles are equal)
y + 110° = 180°
y = 180°- 110° = 70°
z = y ⇒ z = 70°
Hence x = 110°, y = 70° and z = 70°
Question 6.
In the given figure AB ∥ CD and AE is transversal. If ∠BAC =120°, then find x and y.
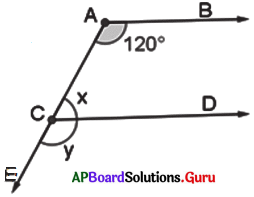
Answer:
In the given figure, AB ∥ CD and AE is transversal.
∠BAC = 120
∠ACD = x
∠DCE = y
∠BAC = ∠DCE (correpsonding angles are equal)
y = 120°
x + y = 180 ° (Linear pair of angles are supplementary)
x + 120° – 180°
x = 180°- 120°
∴ x = 60°
Hence x = 60°, y =120°.
Question 7.
In the given figure, BA ∥ CD and BC is transversal. Find x.
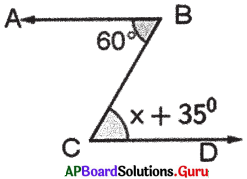
Answer:
In the given figure, BA ∥ CD and BC is transversal.
∠C = x + 35° and ∠B = 60°
∠C = ∠B (∵ alternate interior angles are equal)
x + 35° = 60° .
x – 60° – 35°
∴ x = 25°
Question 8.
In the figure \(\overrightarrow{\mathbf{M N}} \| \overrightarrow{\mathbf{K L}}\) and \(\overline{\mathrm{MK}}\) is transversal. Find x.
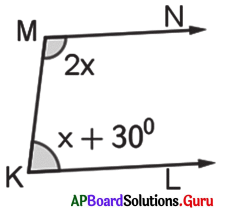
Answer:
From the figure, \(\overrightarrow{\mathbf{M N}} \| \overrightarrow{\mathbf{K L}}\) and \(\overline{\mathrm{MK}}\) is transversal.
∠M = 2x and ∠K = x + 30°
∠M + ∠K = 180° (Q co-interior angles are supplementary)
⇒ 2x + x + 30° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30°
⇒ 3x = 150° ⇒ x = \(\frac{150^{\circ}}{3}\)
∴ x = 50°
![]()
Question 9.
In the figure \(\overline{\mathrm{AB}} \| \overline{\mathrm{DE}}\) and C is a point in between them. Observe the figure, then find x, y and ∠BCD.
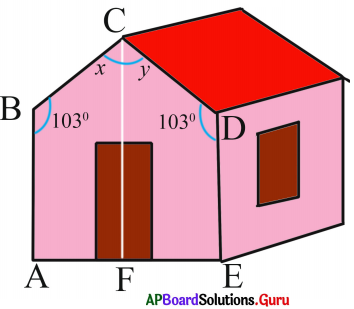
Answer:
In the figure \(\overline{\mathrm{AB}} \| \overline{\mathrm{DE}}\) and C is a point in between them.
Draw a parallel line CF to \(\overline{\mathrm{AB}}\) through C.
\(\overline{\mathrm{AB}} \| \overline{\mathrm{CF}}\) and \(\overline{\mathrm{BC}}\) is a transversal,
x + 103° = 180°
x = 180°- 103°
x = 77°
From the figure,
\(\overline{\mathrm{DC}} \| \overline{\mathrm{CF}}\) and \(\overline{\mathrm{CD}}\) is a transversal,
y + 103° = 180°
y = 180°- 103°
y = 77°
and ∠BCD = x + y = 77° + 77° = 154°
Question 10.
In the figure transversal p intersects two lines m and n. Observe the figure, check whether m ∥ n or not.
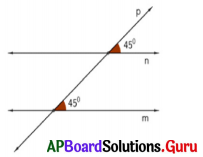
Answer:
In the given figure, it is given that each angle in the pair of corresponding angles is 45°. So they are equal. Since a pair of corresponding angles are equal the lines are parallel. Hence, m ∥ n.
Practice Questions [Page No. 87]
Indicate the group (a, b, c, d, e, f) to which given below belongs to
Question 1.
State, District, Mandai
Answer:
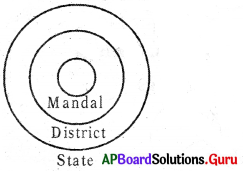
Group: b
Question 2.
Boys, Girls, Artistists
Answer:
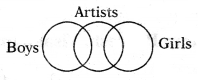
Group: c
Question 3.
Hours, Days, Minutes
Answer:

Group: b
Question 4.
Women, Teacher, Doctor
Answer:

Group: c
Question 5.
Food, Curd, Spoon
Answer:
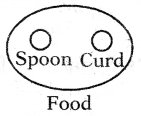
Group: f
![]()
Question 6.
Humans, Dancer. Player
Answer:
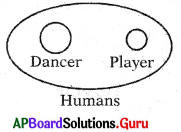
Group: f
Question 7.
Building, Brick, Bridge
Answer:
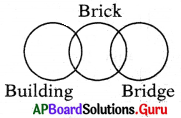
Group: c
Question 8.
Tree, Branch, Leaf
Answer:

Group: b
Question 9.
Gold. Silver, Jewellary
Answer:
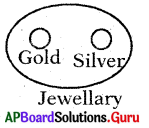
Group: f
Question 10.
Bulbs, Mixtures, Electricals
Answer:
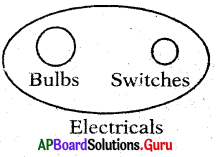
Group: f
![]()
Question 11.
Women, Illiteracy, Men
Answer:
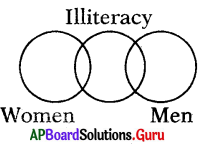
Group: c
Question 12.
Medicine, Tablets. Syrup
Answer:
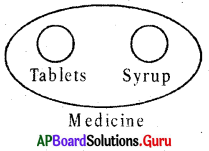
Group: f
Question 13.
Carrots, Oranges, Vegetables
Answer:
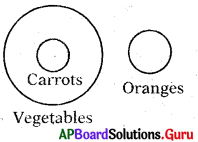
Group: e
Question 14.
Female, Mothers. Sisters
Answer:
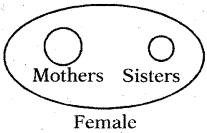
Group: f
Question 15.
Table. Furniture, Chair
Answer:
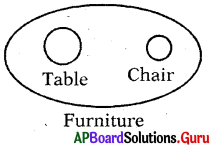
Group: f
Question 16.
Fruits, Mango. Onions
Answer:
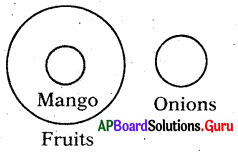
Group: e
Question 17.
School, Teacher, Students
Answer:
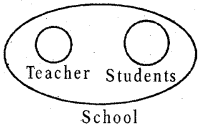
Group: f
Question 18.
Rivers. Oceans. Springs
Answer:
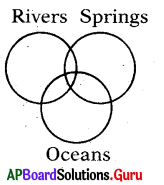
Group: d
Question 19.
India. Andhra Pradesh, Visakhapatnam
Answer:
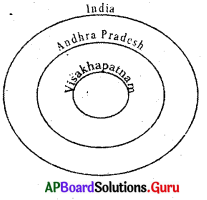
Group: b
Question 20.
Animals. Cows. Horses
Answer:
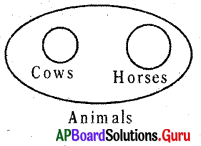
Group: f
Question 21.
Fish. Tiger, snakes
Answer:
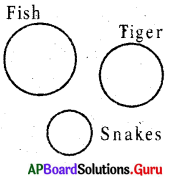
Group: a
![]()
Question 22.
Flowers. Jasmine. Banana
Answer:
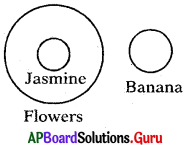
Group: e
Question 23.
Authors, teachers, Men
Answer:
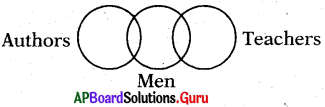
Group: c
Question 24.
Dog. Fish, Parrot
Answer:
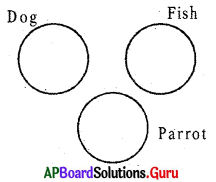
Group: a
Question 25.
Rose, Flower, Apple
Answer:
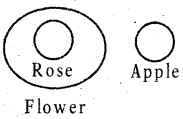
Group: e
Question 26.
School, Benches. Class Room
Answer:

Group: b
Question 27.
Pen, Stationary, Powder
Answer:

Group: e
Question 28.
Crow, Pigeon. Bird
Answer:
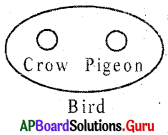
Group: f
Question 29.
Mammals, Elephants, Dinosaurs
Answer:
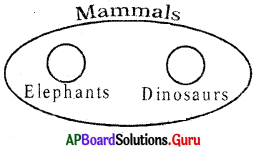
Group: f
Question 30.
Writers. Teachers, Researchers
Answer:
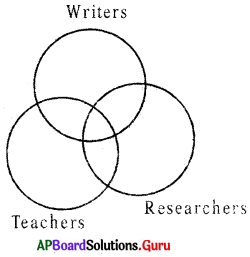
Group: d
REASONING [Practice Questions]
Question 1.
Musician, Instrumentalist, Violinist.
Answer:

Group: b
Question 2.
Officer, Woman, Doctor
Answer:
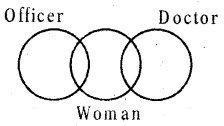
Group: c
![]()
Question 3.
Girls, Students, 7” class girls
Answer:
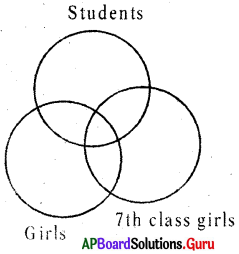
Group: d
Question 4.
Pencil, Stationary, Toothpaste
Answer:

Group: e
Question 5.
Food, Curd, Fruits
Answer:

Group: f
Question 6.
Bird Pigeon, Cow
Answer:

Group: e
Question 7.
Notes, Pad, Pen
Answer:
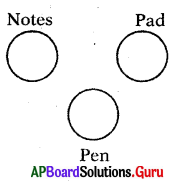
Group: a
Question 8.
Banana, Guava, Apple
Answer:
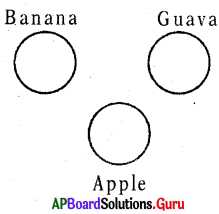
Group: a
Question 9.
Tomato, Food, Vegetables
Answer:
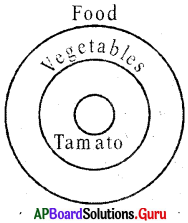
Group: b
![]()
Question 10.
Cow, Dog Pet
Answer:
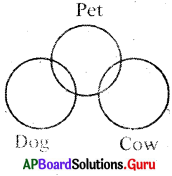
Group: c