AP State Syllabus AP Board 7th Class Maths Solutions Chapter 2 Fractions, Decimals and Rational Numbers Ex 1 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Exercise 1
Question 1.
Solve the following.
(i) 2 + [latex]\frac { 3 }{ 4 }[/latex]
(ii) [latex]\frac{7}{9}+\frac{1}{3}[/latex]
(iii) 1 – [latex]\frac{4}{7}[/latex]
(iv) [latex]2 \frac{2}{3}+\frac{1}{2}[/latex]
(v) [latex]\frac{5}{8}-\frac{1}{6}[/latex]
(vi) [latex]2 \frac{2}{3}+3 \frac{1}{2}[/latex]
Solution:
Question 2.
Arrange the following in ascending order.
(i) [latex]\frac{5}{8}, \frac{5}{6}, \frac{1}{2}[/latex]
(ii) [latex]\frac{2}{5}, \frac{1}{3}, \frac{3}{10}[/latex]
Solution:
Question 3.
Check whether in this square the sum of the numbers in each row and in each column and along the diagonals is the same.
Solution:
Question 4.
A rectangular sheet of paper is 5[latex]\frac{2}{3}[/latex] cm long and 3[latex]\frac{1}{5}[/latex] cm wide. Find its perimeter.
Solution:
Length of the rectangular sheet = 5[latex]\frac{2}{3}[/latex] cm
Breadth/width of the rectangular sheet = 5[latex]\frac{2}{3}[/latex] cm
Perimeter = 2 x (length + breadth)
Question 5.
The recipe requires 3[latex]\frac{1}{4}[/latex] cups of flour. Radha has 1[latex] \frac{3}{8}[/latex] cups of flour. How many more cups of flour does she need?
Solution:
Flour required for the recipe = 3[latex]\frac{1}{4}[/latex] cups
Flour with Radha = 1[latex]\frac{3}{8}[/latex] cups
More cups of flour required = [latex]3 \frac{1}{4}-1 \frac{3}{8}[/latex]
= [latex]\frac{3 \times 4+1}{4}-\frac{1 \times 8+3}{8}[/latex]
Question 6.
Abdul is preparing for his final exam. He has completed [latex]\frac{5}{12}[/latex] part of his course content. Find out how much course content is left?
Solution:
Take content as 1 (i.e., full) Course completed = [latex]\frac{5}{12}[/latex]
Course yet to be completed = 1 – [latex]\frac{5}{12}[/latex]
= [latex]\frac{12 \times 1-5}{12}[/latex]
[latex]\frac{12-5}{12}=\frac{7}{12}[/latex]
Question 7.
Find the perimeters of(i) ΔABE (ii) the rectangle BCDE in this figure. Which figure has greater perimetre and by how much?
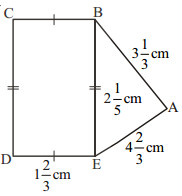
Solution:
i) Perimeter of ΔABE = AB + BE + AE
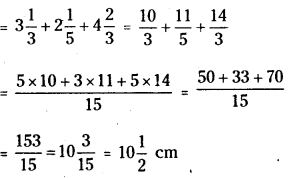
ii) Perimeter of BCDE = 2(BE + BC)
As [latex]\frac{116}{15}<\frac{153}{15}[/latex], we conclude that the perimetre of ΔABE > Perimeter of BCDE