SCERT AP 7th Class Maths Solutions Pdf Chapter 11 Area of Plane Figures Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 11th Lesson Area of Plane Figures Unit Exercise
Question 1.

Answer:

![]()
Question 2.
Write the formulae of the following:
(i) Area of the rectangular path ……………….. .
Answer:
Area of the outer rectangle – Area of the inner rectangle.
(ii) Area of the square path ……………….. .
Answer:
Area of the outer square – Area of the – inner square.
(iii)
Area of the circular path ……………….. .
Answer:
Area of the outer circle – Area of the inner circle.
π(R + r)(R – r)
Question 3.
Find the area of a triangle if its base is 18 cm, height is 13 cm.
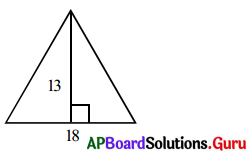
Answer:
Given base of the triangle b = 18 cm
Height of the triangle h = 13 cm
Area of the triangle = \(\frac{1}{2}\) ∙ b ∙ h
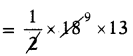
∴ Area of the triangle = 117 sq.cm.
![]()
Question 4.
In a park a rectangular path given outside for walking around the grassland of length 28 m., and breadth 20m. If the width of the walking path is 2m., find the area of walking path.

Answer:
Given inner length of the park l = 28 m
Breadth b = 20 m
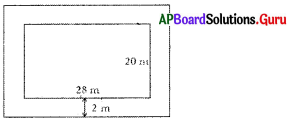
Area of the inner rectangle = l × b
= 28 × 20
= 560 sq.m
Path laid outside around the grassland.
Width of the path = 2 m
So, outer length of rectangle
l = Inner length + 2 × Width
= 28 + 2 × 2 = 28 + 4 = 32 m
Breadth b = 20 + 2 × 2
= 20 + 4 = 24m
Area of the outer rectangle = l × b = 32 × 24 = 768 sq.m
∴ Area of the walking path = outer area – inner area
= 768 – 560 = 208 sq.m.
![]()
Question 5.
The elevation of building have square – shaped window of a side 150 cm. Around this window tiles arranged with a width of 70 cm. Find the area of tiles and total cost of tiles arranged, if cost per sq.cm. is ₹ 5.
Answer:
Side of square window = 150 cm
Area of square window = 150 × 150 A
= 22500 cm2
Area of square formed by arranging tiles around the window
= (150 + 70)2 = 2202 = 48400 cm2
Area of tiles laid = (Area of outer square) – Area of inner square
= 48400 – 22500 = 25900
∴ Total cost by laying tiles around the window
@ ₹5 per cm2 is = 259 × 5 = ₹ 1295.00
Question 6.
Two cross roads, each of width 4 m, run at right angles through the centre of a rectangular park of length 60 m and breadth 40 m and parallel to its sides. Find the area of the roads. Also find the cost of constructing the roads at the rate of ₹ 100 sq.m.

Answer:
Length of the rectangular park = 60 m
Breadth of the rectangular park = 40 m
Length of the path along length of the park = 60 m
Width of the path along length of the park = 40 m
Area of the path along length of the park = 60 × 4 = 240 m2
Similarly,
Length of the path along breadth of the park = 40 m
Width = 4m
∴ Area of the path along its breadth = 40 × 4 = 160 m2
Hence, area of the paths = Area of the path along length + Area of the path along breadth – Area of the intersecting square
= 240 + 160 – 4 × 4
= 400 – 16 = 384
∴ Cost of construction at the rate of
₹ 100 per sq.m = 384 × 100 = ₹ 38400
![]()
Question 7.
Find the area of the circular shaped photo frame whose radius 28 cm. If the cost of decoration is ₹ 3 per sq. cm., find total cost of decoration.
Answer:
Radius of the circle = 28 cm
Area = πr2
= \(\frac{22}{7}\) × 28 × 28 = 2464 cm2
Circumference of the photo frame 2πr
= 2 × \(\frac{22}{7}\) × 28 = 176 cm
∴ Cost of decorative piece at the rate of ₹ 3 per cm is 176 × 3 = ₹ 528
Question 8.
Find the path area of circular shaped grassland of radius 42 m where width of the path is 7 m. around and outside the circle. Find the area of path and total cost of flooring, if the cost of flooring ₹ 150 per sq.m.

Answer:
Radius of circular floor = 42 m
Width around it = 7 m
Radius of outer circle = 42 + 7 = 49 m
Area of outside path = Area of outer circle – Area of inner cirlce
Area of inner circle = πr2 = \(\frac{22}{7}\) × 42 × 42
Area of the outer circle = πR2 = \(\frac{22}{7}\) × 49 × 49
Area of floor = \(\frac{22}{7}\) (49 × 49 – 42× 42)
= \(\frac{22}{7}\) (2401 – 1764)
= \(\frac{22}{7}\) × 637 = 2002 m2
∴ Cost of flooring at the rate of ₹ 150 per sq.m is 2002 × 150 = ₹ 300300