SCERT AP 7th Class Maths Solutions Pdf Chapter 10 Construction of Triangles InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 10th Lesson Construction of Triangles InText Questions
[Page No. 67]
Look at the picture and answer the following questions

Question 1.
Name some things from your daily life that look like triangles.
Answer:
Samosa, chapathi, window elevations, house tops, bridge trusses, floor tessellations.
Question 2.
What are the types of triangles can see in the picture?
Answer:
Right triangles,
Equilateral triangles.
Question 3.
Do you think all triangles shown are similar with their properties? What are they?
Answer:
Yes. All right triangles are similar.
All triangles are similar because they have
(a) right angle
(b) equal side and
(c) equal hypotenuse.
![]()
Check Your Progress [Page No. 69]
Question 1.
Construct an equilateral triangle ∆XYZ with XY = 4 cm.
Answer:
Given sides of an equilateral triangle ∆XYZ is XY = 4 cm.
In equilateral triangle all sides ,gresequal in length
∴ XY = YZ = ZX = 4 cm.
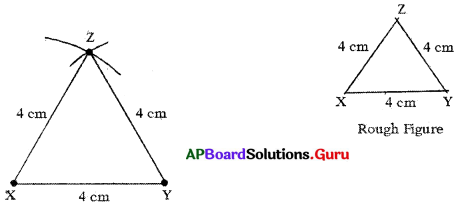
Steps of Construction:
- Draw a rough sketch of the triangle and label it with the given measurements.
- Draw a line segment with XY = 4 cm,
- Draw an arc with centre X and radius 4 cm.
- Draw another arc with centre Y and radius 4 cm to intersecting the previous arc at Z.
- Join XZ andYZ.
Hence, required ∆XYZ is constructed with the given measurements.
Question 2.
Construct an isosceles triangle ∆PQR With PQ = PR = 3 cm, QR = 5 cm.
Answer:
Given sides of an isosceles triangle ∆PQR are PQ = PR = 3 cm and QR = 5 cm
In isosceles triangle two sides are equal.
∴ PQ = PR = 3 cm

Steps of construction:
- Draw a rough sketch of the triangle and label it with the given measurements.
- Draw a line segment QR = 5 cm.
- Draw an arc with centre Q and radius 3 cm.
- Draw another arc with centre R and same radius (3 cm) to intersect the previous arc at P.
- Join PQ and PR.
Hence, required APQR is constructed with the given measurements.
Let’s Think [Page No. 69]
Can you construct ∆ABC with AB = 4 cm, BC = 5 cm and CA =10 cm? Why? Justify your answer.
Answer:
Given sides of a ∆ABC are AB = 4 cm, BC = 5 cm and CA =10 cm.
In any triangle sum of any two sides is always greater than the third side.
AB + BC = 4 cm + 5 cm = 9 cm <10 cm.
Sum of AB + BC < AC
So, with the given measurements construction of ∆ABC is not possible.
Check Your Progress [Page No. 72]
Question 1.
Construct ∆MAT with measurements MA = 5.5 cm, MT = 4 cm and ∠M=70°.
Answer:
Given measurements of ∆MAT are MA = 5.5 cm, MT = 4 cm and ∠M = 70°.
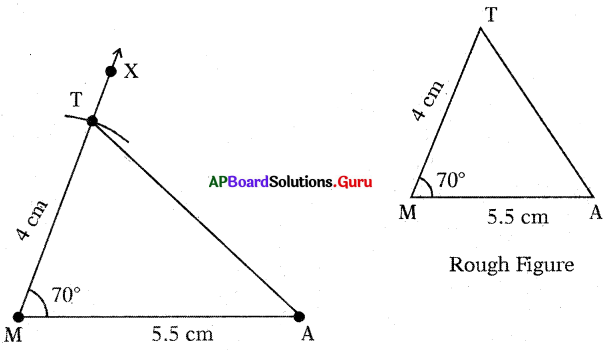
Steps of Construction:
- Draw a rough sketch of the triangle and label it with the given measurements.
- Draw a line segment with MA = 5.5 cm.
- Draw a ray \(\overrightarrow{\mathrm{MX}}\) such that ∠AMX = 70°
- Draw an arc with centre M and radius 4 cm, to intersect the \(\overrightarrow{\mathrm{MX}}\) at point T.
- Join AT.
Hence, required ∆MAT is constructed with the given measurements.
![]()
Let’s Explore [Page No. 72]
Question 1.
Construct the triangle with the measurements of AB = 7cm, ∠B = 60° and ∠C = 70°.
Answer:
Given measurements of ∆ABC are AB = 7 cm, ∠B = 60° and ∠C = 70°.
In ∆ABC, ∠A + ∠B + ∠C = 180°
∠A + 60° + 70° = 180° .
∠A + 130° = 180°
∠A = 180° – 130° = 50°
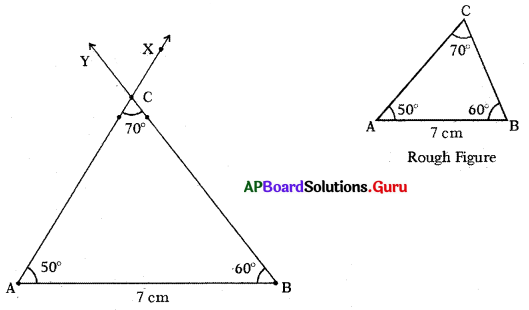
Steps of Construction:
- Draw a rough sketch of triangle and label it with given measurements.
- Draw a line segment with AB = 7 cm.
- Draw a ray BY such that ABY = 60°.
- Draw another ray AX such that BAX = 50°.
- Name the intersecting of rays AX and BY is C.
Hence, required ∆ABC is constructed with the given measurements.
Check Your Progress [Page No. 73]
Question 1.
Construct ∆ABC with the measurements ∠A = 90°, ∠C = 50° and AC = 8 cm.
Answer:
Given measurements of ∆ABC are ∠A = 90°, ∠C = 50° and AC = 8 cm.
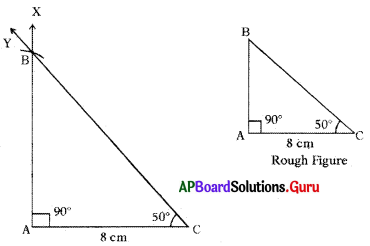
Steps of Construction:
- Draw a rough sketch of triangle and label it with given measurements.
- Draw a line segment with AC = 8 cm.
- Draw a ray AX such that ∠CAX = 90°.
- Draw another ray CY such that ∠ACY = 50°.
- Name the intersecting point of AX and CY as B.
Thus, required ∆ABC is constructed with the given measurements.
Let’s Think [Page No. 73]
Construct a triangle with angles 100°, 95° and a side of length of your choice. Can1 you construct the triangle?
Answer:
No. It is not possible. We know that the sum of the angles of a triangle is 180°.
But, given two angles are 100° and 95°. Their sum is greater than 180°.
So, we cannot construct the triangle.
Examples:
Question 1.
Construct ∆ABC with slides AB = 6 cm, BC = 4 cm and AC = 5 cm.
Answer:
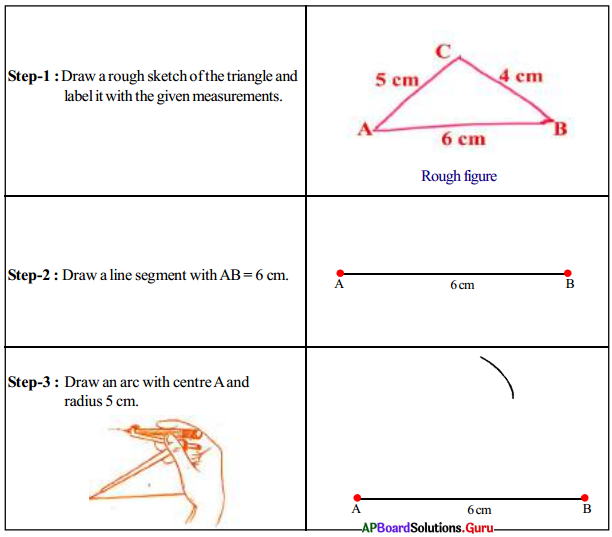
Question 2.
Construct ∆EFD with the measurements ∠F = 70°, EF = 4 cm and FD = 5 cm.
Answer:
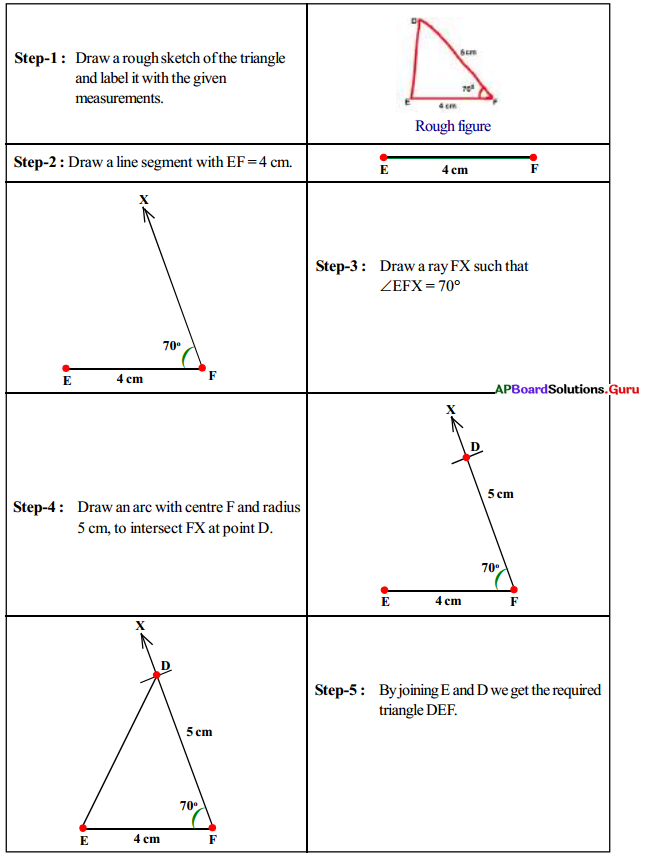
![]()
Question 3.
Construct ∆ABC with AB = 6 cm, BC = 7 cm, ∠BAC = 80°.
Answer:
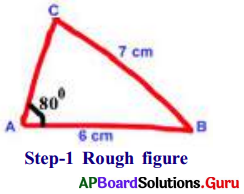
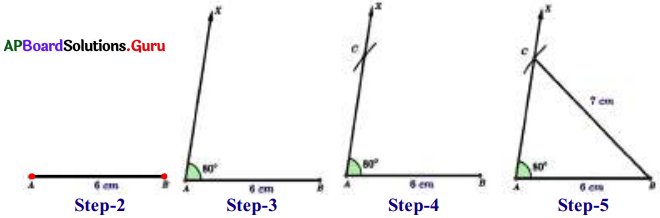
- Step-1: Draw a rough sketch of ∆ABC and label it with the given measurements.
- Step-2: Draw a line segment AB of length 6 cm.
- Step-3: Draw a ray AX such that ∠BAX = 80°.
- Step-4: Draw an arc with center B and radius 7 cm to Intersect the ray AX at C.
- Step-5: Join B and C to get the required ∆ABC.
Question 4.
Construct a right angled triangle ∆XYZ, XY = 4 cm, XZ = 6.5 cm and ∠Y = 90°.
Answer:
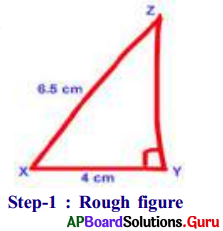
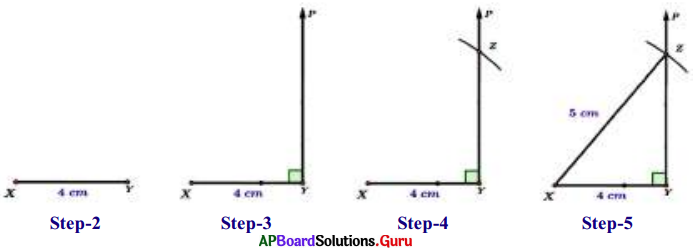
- Step-1: Draw a rough sketch of ∆XYZ and label it with given measurements.
- Step-2: Draw a line segment with XY = 4 cm.
- Step-3: Draw a ray YP such that ∠XYP = 90°.
- Step-4: Draw an arc with center X and radius 6.5 cm to intersect the Ray YP at Z.
- Step-5: Join X and Z to get the required ∆XYZ.
Question 5.
Construct ∆PEN with measurements PE. = 7 cm, ∠PEN = 25° and ∠EPN = 60°
Answer:
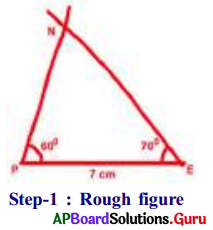
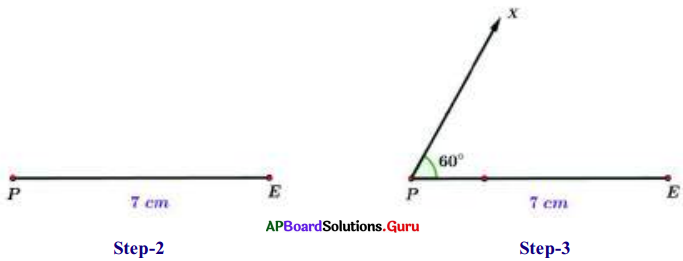
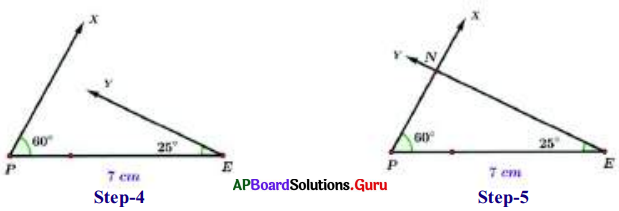
- Step-1: Draw a rough sketch of the triangle and label it with given measurements.
- Step-2: Draw a line segment with PE = 7 cm,
- Step-3: Draw a ray PX such that ∠EPX = 60°.
- Step-4: Draw another ray EY such that ∠PEY = 25°.
- Step-5: Rays PX and EY intersect each other at N.
Hence, we get the required ∆PEN.
(If necessary, extend the rays to form a triangle.)
Question 6.
Construct ∆MPC the triangle with the measurements MP = 4 cm, ∠P = 45° arid ∠C = 80°.
Answer:
Now we have to find out the third angle.
We know that the sum of three angles in a triangle is 1800.
So, ∠M + ∠P + ∠C = 180°
⇒ ∠M + 450 + 80° = 180°
⇒ ∠M + 125° = 180°
⇒ ∠M = 180 – 125 = 55°
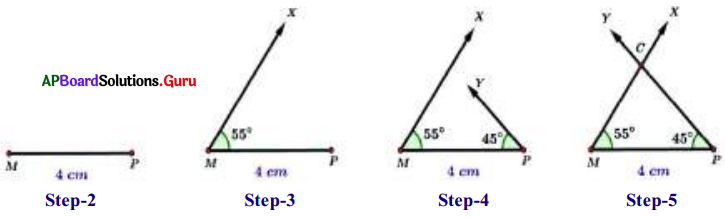
- Step-1: Draw a rough sketch of the triangle and label it with given measurements.
- Step-2: Draw a line segment with MP = 4 cm.
- Step-3: Draw a ray MX such that ∠PMX = 55°.
- Step-4: Draw another ray PY such that ∠MPY = 45°.
- Step-5: Rays MX and PY intersect each other at C. (If necessary extend the rays to ‘ form a triangle.)
Hence, we get the required ∆MPC.
Verification: By using the protractor and check whether ∠C is equal to 80° or not.
![]()
Practice Questions [Page No. 78]
Find the number of triangles in the given figures.
Question 1.

(a) 8
(b) 9
(c) 10
(d) 12
Answer:
(b) 9
Explanation:
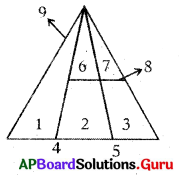
Question 2.

(a) 60
(b) 65
(c) 84
(d) 90
Answer:
(a) 60
Explanation:
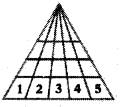
Number of rows = 4
Sum of numbers in each row = 1 + 2 + 3 + 4 + 5 = 15
Number of triangles in the picture = 4 × 15 = 60
Question 3.

(a) 12
(b) 13
(c) 14
(d) 15
Answer:
(b) 13
Explanation:
Formula to count number of triangles = 4n + 1
Here n = number of embedded triangles in outer triangle
In the figure n = 3
So, number of triangles = 4(3) + 1 = 12 + 1 = 13
Question 4.

(a) 16
(b) 13
(c) 9
(d) 7
Answer:
(a) 16
Question 5.
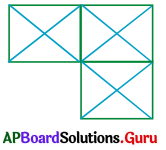
(a) 21
(b) 23
(c) 25
(d) 29
Answer:
(d) 29
Explanation:

Question 6.
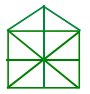
(a) 10
(b) 19
(c) 21
(d) 23
Answer:
(c) 21
Explanation:

Question 7.

Answer:
(a) 5
(b) 6
(c) 8
(d) 10
Answer:
(c) 8
![]()
Question 8.

(a) 9
(b) 10
(c) 11
(d) 12
Answer:
(a) 9
Explanation:

Question 9.

(a) 19
(b) 20
(c) 16
(d) 14
Answer:
(a) 19
Question 10.

(a) 56
(b) 48
(c) 32
(d) 60
Answer:
(b) 48
Explanation:
Formula to count number of triangles = \(\frac{\mathrm{n}(\mathrm{n}+2)(2 \mathrm{n}+1)}{8}\)
Where n = number of thangles formed in a side
Here in the given figure n = 5
Number of triangles = \(\frac{5(5+2)(2 \times 5+1)}{8}=\frac{5 \times 7 \times 11}{8}\) = 48.1
So, total number of triangles = 48.