AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra Unit Exercise Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra Unit Exercise
Question 1.
The cost of one fan is Rs. 1500. Then what is the cost of ‘n’ fans?
Answer:
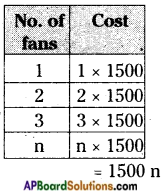
Given cost of one fan = Rs. 1500
Number of fans = n
Cost of n fans = cost of one fan × no. of fans = 1500 × n
∴ Cost of n fans = 1500n
Question 2.
Srinu has number of pencils. Raheem has 4 times the pencils as of Srinu. How many pencils does Rahim has? Write an expression.
Answer:
Let number of pencils Srinu has = x
Number of pencils Raheem has = 4 times of Srinu
= 4 × x
∴ Number of pencils Raheem has = 4x
![]()
Question 3.
Parvathi has 5 more books than Sofia. How many books are with Parvathi? Write an expression choosing any variable for number of books.
Answer:
Let number of books Sofia has = y
Given Parvathi has 5 more books than Sofia
Number of books Parvathi has = 5 books more than Sofia
= y + 5
∴ Number of books Parvathi has = y + 5
Question 4.
Which of the following are equations?
i) 10 – 4p = 2
ii) 10 + 8x < – 22
iii) x + 5 = 8
iv) m + 6 = 2
v) 22x – 5 = 8
vi) 4k + 5 > – 100
vii) 4p + 7 = 23
viii) y < – 4
Answer:
i) 10 – 4p = 2
We know that, a mathematical statement involving equality symbol is called an equation.
10 – 4p = 2 has equality symbol.
So, it is an equation.
ii) 10 + 8x < – 22
We know that, a mathematical statement involving equality symbol is called an equation.
10 + 8x < – 22 has no equality symbol.
So, it is not an equation [so it is an inequation]
iii) x + 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
x + 5 = 8 has equality symbol.
So, it is an equation.
![]()
iv) m + 6 = 2 We know that, a mathematical statement involving equality symbol is called an equation.
m + 6 = 2 has equality symbol.
So, it is an equation.
v) 22x – 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
22x – 5 = 8 has equality symbol.
So, it is an equation.
vi) 4k + 5 > – 100
We know that, a mathematical statement involving equality symbol is called an equation.
4k + 5 > -100 has no equality symbol.
So, it is not an equation.
It is an inequation.
vii) 4p + 7 = 23
We know that, a mathematical statement involving equality symbol is ailed an equation.
4p + 7 = 23 has equality symbol.
So, it is an equation.
viii) y < – 4
We know that, a mathematical statement involving equality symbol is called an equation.
y < – 4 has no equality symbol.
So, it is not an equation.
It is an inequation.
Question 5.
Write L.H.S and R.H.S of the following equations:
i) 7x + 8 = 22
ii) 9y – 3 = 6
iii) 3k – 10 = 2
iv) 3p – 4q = -19
Answer:
i) 7x + 8 = 22
Given equation is 7x + 8 = 22
LHS = 7x + 8
RHS = 22
ii) 9y – 3 = 6
Given equation is 9y – 3 = 6
LHS = 9y – 3
RHS = 6
iii) 3k – 10 = 2
Given equation is 3k – 10 = 2
LHS = 3k – 10
RHS = 2
![]()
iv) 3p – 4q = -19
Given equation is 3p – 4q = -19
LHS = 3p – 4q
RHS = -19
Question 6.
Solve the following equations by trial and error method.
i) x – 3 = 5
ii) y + 6 = 15
iii) y = -1
iv) 2k – 1 = 3
Answer:
i) x – 3 = 5
Given equation is x – 3 = 5
If x = 1, then the value of x – 3 = 1 – 3 = -2 ≠ 5
If x = 2, then the value of x – 3 = 2 – 3 = -l ≠ 5
If x = 3, then the value of x – 3 = 3 – 3 = 0 ≠ 5
If x = 4, then the value of x – 3 = 4 – 3 = l ≠ 5
If x = 5, then the value of x – 3 = 5 – 3 = 2 ≠ 5
If x = 6, then the value of x – 3 = 6 – 3 = 3 ≠ 5
If x = 7, then the value of x – 3 = 7 – 3 = 4 ≠ 5
If x = 8, then the value of x – 3 = 8 – 3 = 5 = 5
From the above when x = 8, the both LHS and RHS are equal.
∴ Solution of the equation x – 3 = 5 is x = 8
ii) y + 6 = 15
Given equation is y + 6 = 15
If y = 1, then the value of y + 6 = 1 + 6 = 7 ≠ 15
If y = 2, then the value of y + 6 = 2 + 6 = 8 ≠ 15
If y = 3, then the value of y +6 = 3 + 6 = 9 ≠ 15
If y = 4, then the value of y + 6 = 4 + 6 = 10 ≠ 15
If y = 5, then the value of y + 6 = 5 + 6 = 11 ≠ 15
If y = 6, then the value of y + 6 = 6 + 6 = 12 ≠ 15
If y = 7, then the value hf y + 6 = 7 + 6 = 13 ≠ 15
If y = 8, then the value of y + 6 = 8 + 6 = 14 ≠ 15
If y = 9, then the value of y + 6 = 9 + 6 = 15 = 15
From the above when y = 9, the both LHS and RHS are equal.
∴ Solution of the equation y + 6 = 15 is y = 9
![]()
iii) \(\frac{m}{2}\) = -1
Given equation is \(\frac{m}{2}\) = -1
If m = 1, then the value of \(\frac{m}{2}\) = \(\frac{1}{2}\) ≠ -1
If m = 2, then the value of \(\frac{m}{2}\) = \(\frac{2}{2}\) = 1 ≠ -1
If m = 3, then the value of \(\frac{m}{2}\) = \(\frac{3}{2}\) ≠ -1
Here, we are not getting negative values.
If we take (substitute) m as a negative number we will get negative value.
If m = -1, then the value of \(\frac{m}{2}\) = \(\frac{-1}{2}\) ≠ -1
If m = -2, then the value of \(\frac{m}{2}\) = \(\frac{-2}{2}\) = -1 = -1
From the above when m = -2, the both LHS and RHS are equal.
∴ Solution of the equation \(\frac{m}{2}\) = -1 is m = -2.
iv) 2k – 1 = 3
Given equation is 2k – 1 = 3
If k = 1, then the value of 2k – 1 = 2(1) – 1 = 2 – 1 = 1 ≠ 3
If k = 2, then the value of 2k – 1 = 2(2) – 1 = 4 – 1 = 3 = 3
From the above when k – 2, the both LHS and RHS are equal.
Solution of the equation 2k – 1 = 3 is k = 2.