SCERT AP 6th Class Maths Solutions Chapter 6 ప్రాథమిక అంకగణితం InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 6th Lesson ప్రాథమిక అంకగణితం InText Questions
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 89]
ప్రశ్న 1.
45, 70 లను నిష్పత్తి గుర్తును ఉపయోగించి రాయండి.
సాధన.
ఇవ్వబడిన సంఖ్యలు 45 మరియు 70
నిష్పత్తి = 45 : 70
దీనిని 45 ఈజ్ టు 70 గా చదువుతాము.
ప్రశ్న 2.
7 : 15 నందు పూర్వ పదంను రాయండి.
సాధన.
ఇవ్వబడిన నిష్పత్తి 7 : 15
నిష్పత్తిలో మొదటి పదమును పూర్వపదం అంటారు.
7 : 15 లో పూర్వపదం = 7.
ప్రశ్న 3.
8 : 13 నందు పరపదంను రాయండి.
సాధన.
ఇవ్వబడిన నిష్పత్తి 8 : 13
నిష్పత్తిలో రెండవ పదమును పరపదం అంటారు.
8 : 13 లో పరపదం = 13.
ప్రశ్న 4.
35:55 ను కనిష్ఠ రూపంలో రాయండి.
సాధన.
ఇవ్వబడిన నిష్పత్తి 35 : 55 (లేదా)
ఈ నిష్పత్తిని సామాన్య రూపంలోకి రాయవలెనన్న 35 మరియు 55 ల ఉమ్మడి కారణాంకం ‘5’ చే భాగించవలెను.
ఉమ్మడి కారణాంకం 5.
ఇప్పుడు ‘5’ చే భాగించగా,
\(\frac{35}{55}=\frac{35 \div 5}{55 \div 5}=\frac{7}{11}\)
35 : 55 = \(\frac{35}{5}: \frac{55}{5}\) = 5 : 11
![]()
ప్రశ్న 5.
పక్కపటం నుండి కింది నిష్పత్తులు కనుగొనండి.

అ) రంగు వేసిన భాగము, రంగు వేయని భాగం.
ఆ) రంగు వేసిన భాగము, మొత్తం భాగం.
ఇ) రంగు వేయని భాగము, మొత్తం భాగం.
సాధన.
అ) ఇవ్వబడిన పటంలో,
రంగు వేసిన భాగము = 1
రంగు వేయని భాగము = 3
నిష్పత్తి = రంగువేసిన భాగము : రంగువేయని భాగము = 1 : 3
ఆ) రంగువేసిన భాగము = 1
మొత్తం భాగములు = 4
నిష్పత్తి = రంగువేసిన భాగము : మొత్తం భాగములు = 1 : 4
ఇ) రంగు వేయని భాగము = 3
మొత్తం భాగములు = 4
నిష్పత్తి = రంగువేయని భాగము : మొత్తం భాగములు = 3 : 4
ప్రశ్న 6.
కింది వాటిని నిష్పత్తి రూపంలో రాయండి.
అ) దీర్ఘచతురస్రం యొక్క పొడవు, వెడల్పునకు మూడు రెట్లు.
ఆ) ఒక పాఠశాలలో 19 సెకన్ల పనిభారం 38 మంది ఉపాధ్యాయులకు కుదించబడింది.
సాధన.
అ) దీర్ఘచతురస్రం యొక్క వెడల్పు = x లేదా ఒక భాగం = 1 భాగం
దీర్ఘచతురస్రం యొక్క పొడవు = వెడల్పునకు మూడు రెట్లు
= 3 × X = 3x = 3 భాగాలు
నిష్పత్తి = l : b = 3x : x = \(\frac{3 x}{1 x}\) = \(\frac {3}{1}\) = 3 : 1
పొడవు : వెడల్పు = 3 : 1
ఆ) ఇవ్వబడిన సెక్షన్లు = 19
ఉపాధ్యాయుల సంఖ్య = 38
∴ నిష్పత్తి = సెక్షన్లు : ఉపాధ్యాయులు = 19 : 38
\(\frac{19}{38}: \frac{1}{2}\) = 1 : 2
[పేజి నెం. 93]
ప్రశ్న 1.
కింది వాటిలో ఏ నిష్పత్తులు పెద్దవి?
అ) 5 : 4 లేదా 9 : 8
ఆ) 12 : 14 లేదా 16 : 18
ఇ) 48 : 20 లేదా 12 : 15
ఈ) 4 : 7 లేదా 7 : 11
సాధన.
అ) 5 : 4 లేదా 9 : 8
ఇవ్వబడిన నిష్పత్తులను భిన్నరూపంలో రాయగా,
5 : 4 = \(\frac {5}{4}\) మరియు 9 : 8 = \(\frac {9}{8}\)
హారాలు 4 మరియు 8 ల క.సా.గు = 8
ప్రతి భిన్నం యొక్క హారం ‘8’ వచ్చే విధంగా రాయగా,
\(\frac{5}{4} \times \frac{2}{2}=\frac{10}{8}\) మరియు \(\frac{9}{8} \times \frac{1}{1}=\frac{9}{8}\)
10 > 9 అని మనకు తెలుసు.
\(\frac {10}{8}\) > \(\frac {9}{8}\) లేదా 10 : 8 > 9 : 8
10 : 8 అనునది 5 : 4 కి సమానం .
∴ 5 : 4 అనునది పెద్దది.
ఆ) 12 : 14 లేదా 16 : 18
ఇవ్వబడిన నిష్పత్తులను భిన్నరూపంలో రాయగా,
12 : 14 = \(\frac {12}{14}\) = \(\frac {6}{7}\) మరియు
16 : 18 = \(\frac {16}{18}\) = \(\frac {8}{9}\)
హారాలు 7 మరియు 9 ల క.సా.గు = 63.
ప్రతిభిన్నం యొక్క హారం ’63’ వచ్చే విధంగా రాయగా,
\(\frac{6}{7} \times \frac{9}{9}=\frac{54}{63}\) మరియు \(\frac{8}{9} \times \frac{7}{7}=\frac{56}{63}\)
54 < 56 అని మనకు తెలుసు.
\(\frac {54}{63}\) < \(\frac {56}{63}\) (లేదా) 54 : 63 < 56 : 63
56 : 63 అనునది 16 : 18 (లేదా) 8 : 9కి సమానం
∴ 16 : 18 అనునది పెద్దది.
ఇ) 8 : 20 లేదా 12 : 15
ఇవ్వబడిన నిష్పత్తులను భిన్న రూపంలో రాయగా,
8 : 20 = \(\frac {8}{20}\) = \(\frac {2}{5}\) మరియు
12 : 15 = \(\frac {12}{15}\) = \(\frac {4}{5}\)
\(\frac {2}{5}\) మరియు \(\frac {4}{5}\)
\(\frac {2}{5}\) < \(\frac {4}{5}\) అని మనకు తెలుసు.
2 : 5 < 4 : 5 (లేదా) 8 : 20 < 12 : 15
12 : 15 అనునది పెద్దది.
ఈ) 4 : 7 లేదా 7 : 11
ఇవ్వబడిన నిష్పత్తులను భిన్నరూపంలో రాయగా,
4 : 7 = \(\frac {4}{7}\) మరియు 7 : 11 = \(\frac {7}{11}\)
హారాలు 7 మరియు 11 ల క.సా.గు = 77.
ప్రతిభిన్నం యొక్క హారం ’77’ వచ్చే విధంగా రాయగా,
\(\frac{4}{7} \times \frac{11}{11}=\frac{44}{77}\) మరియు \(\frac{7}{11} \times \frac{7}{7}=\frac{49}{77}\)
\(\frac {44}{77}\) మరియు \(\frac {49}{77}\)
44 < 49 అని మనకు తెలుసు.
\(\frac {44}{77}\) < \(\frac {49}{77}\)(లేదా) 44 : 17 < 49 : 77
4 : 7 < 7 : 11
7 : 11 అనునది పెద్దది.
ప్రశ్న 2.
12 : 16 నిష్పత్తికి సమాన నిష్పత్తులను రాయండి.
సాధన.
ఇవ్వబడిన నిష్పత్తి 12 : 16
ఆ నిష్పత్తిని భిన్న రూపంలో రాయగా
12 : 16 = \(\frac {12}{16}\) = \(\frac {3}{4}\)
ఇపుడు \(\frac {3}{4}\) యొక్క సమాన నిష్పత్తులను రాయగా,
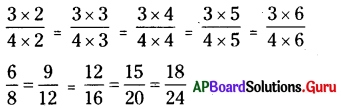
6 : 8 = 9 : 12 = 12 : 16 = 15 : 20 = 18 : 24
∴ 12 : 16 యొక్క సమాన నిష్పత్తులు 6 : 8, 9 : 12, 12 : 16, 15 : 20 మరియు 18 : 24.
![]()
[పేజి నెం. 95]
కింది పదాలు అనుపాతంలో ఉన్నవో, లేవో సరిచూడండి.
అ) 5, 6, 7, 8
అ) 3, 5, 6, 10
ఇ) 4, 8, 7, 14
ఈ) 2, 12, 3, 18
సాధన.
అ) ఇవ్వబడినవి 5, 6, 7, 8
a, b, c, d లు అనుపాతంలో ఉంటే a : b :: c : d
5, 6, 7, 8 లు అనుపాతంలో ఉంటే 5 : 6 :: 7 : 8
అంత్యముల లబ్ధం = మధ్యముల లబ్ధం = ![]()
5 × 8 = 6 × 7
40 ≠ 42
కావున, 5, 6, 7, 8 లు అనుపాతంలో లేవు.
ఆ) ఇవ్వబడినవి 3, 5, 6, 10
a, b, c, d లు అనుపాతంలో ఉంటే a : b :: c : d
3, 5, 6, 10 లు అనుపాతంలో ఉంటే 3 : 5 : : 6 : 10
అంత్యముల లబ్దం = మధ్యముల లబ్దం ![]()
3 × 10 = 5 × 6
30 = 30
కావున 3, 5, 6, 10 లు అనుపాతంలో కలవు.
ఇ) ఇవ్వబడినవి 4, 8, 7, 14.
a, b, c, d లు అనుపాతంలో ఉంటే a : b :: c : d
4, 8, 7, 14 లు అనుపాతంలో ఉంటే 4 : 8 :: 7 : 14
అంత్యముల లబ్దం = మధ్యముల లబ్దం ![]()
4 × 14 = 8 × 7
56 = 56
కావున 4, 8, 7, 14 లు అనుపాతంలో కలవు.
ఈ) ఇవ్వబడినవి 2, 12, 3, 18
a, b, c, d లు అనుపాతంలో ఉంటే a : b :: c : d
2, 12, 3, 18 లు అనుపాతంలో ఉంటే 2 : 12 :: 3 : 18
అంత్యముల లబ్ధం = మధ్యముల లబ్దం ![]()
2 × 18 = 12 × 3
36 = 36
కావున 2, 12, 3, 18 లు అనుపాతంలో కలవు.
![]()
ప్రయత్నించండి [పేజి నెం. 97]
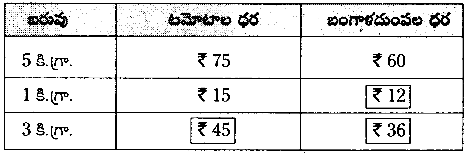
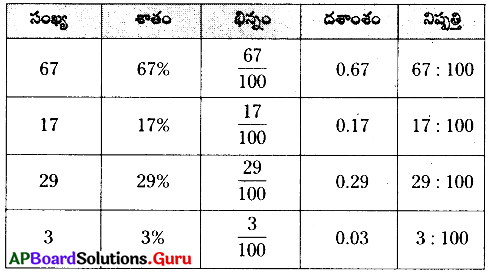
కింది పట్టికను పరిశీలించి, ఖాళీలను పూరించండి.
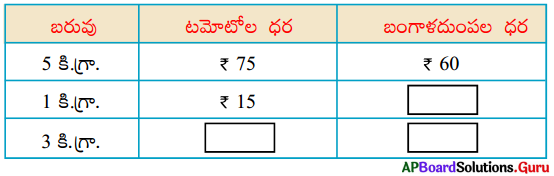
ఇటువంటి సమస్యలను రెండు తయారు చేసి, నీ స్నేహితులకు ఇచ్చి సాధించమనండి.
సాధన.
[పేజి నెం. 99]
కింది పట్టికలో ఇవ్వబడిన వాటిని మిగిలిన రూపాలలో రాయండి.
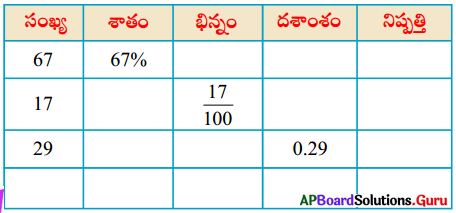
సాధన.
![]()
ఉదాహరణలు
ప్రశ్న 1.
150, 400 లను నిష్పత్తి గుర్తుని ఉపయోగించి కనిష్ఠ రూపంలో రాయండి.
సాధన.
ఇచ్చిన నంబర్లు 150 మరియు 400.
150, 400 ల నిష్పత్తి 150 : 400 = 15 : 40 = 3 : 8
∴ నిష్పత్తి కనిష్ఠ రూపం = 3 : 8
మరొక పద్ధతి :
ఇవ్వబడిన సంఖ్యలు 150 మరియు 400.
భాగహారం ద్వారా సరిపోల్చగా = \(\frac{150}{400}=\frac{15}{40}=\frac{3}{8}\)
∴ నిష్పత్తి కనిష్ఠ రూపం = 3 : 8
ప్రశ్న 2.
కింది నిష్పత్తులను కనిష్ఠ రూపంలో రాయండి.
(i) 28 : 84
(ii) 250 గ్రా॥కు 5 కిలోగ్రాములు
(iii) 24 నిమిషాలకు 3 గంటలు
(iv) 200 మి॥లీ.కు 3 లీ.
సాధన.
i) ఇవ్వబడినవి 28 : 84
28 = 1 × 28
= 2 × 14
= 4 × 7
84 = 1 × 84
= 2 × 42
= 3 × 28
= 4 × 21
= 6 × 14
= 7 × 12
28కి కారణాంకాలు 1, 2, 4, 7, 14, 28.
84 కి కారణాంకాలు 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 లు.
28 మరియు 84 కి సామాన్య కారణాంకాలు = 1, 2, 4, 7, 14, 28.
∴ 28 మరియు 84 ల గ.సా.కా = 28.
కావున రెండు సంఖ్యలను గ.సా.కా (28) చే భాగించవలెను. ఆ విధంగా చేసిన
28 ÷ 28 : 84 ÷ 28 = 1 : 3 లేదా
ఇవ్వబడింది = 28 : 84
= 14 : 42 (రెండు పదాలను 2 చే భాగించగా)
= 7 : 21 (రెండు పదాలను 2 చే భాగించగా)
= 1 : 3 (రెండు పదాలను 7 చే భాగించగా)
∴ నిష్పత్తి కనిష్ఠ రూపం = 1 : 3
ii) ఇవ్వబడినది 250 గ్రాములకు 5 కి.గ్రా.
1 కి.గ్రా. = 1000 గ్రాములు
250 గ్రాములకు 5 కి.గ్రా. = 250 : 5 × 1000
= 250 : 5000
= 25 : 500
= 5 : 100
= 1 : 20
∴ కావలసిన నిష్పత్తి = 1 : 20
iii) 24 నిమిషాలకు 3 గంటలు
1 గంట = 60 నిమిషాలు
3 గంటలు = 3 × 60 = 180 నిమిషాలు.
24 నిమిషాలకు 3 గంటలు = 24 : 180
= 12: 90
= 4 : 30
= 2 : 15
iv) 200 మి.లీ॥కు 3 లీటర్లు
మనకు తెలుసు 1 లీటరు = 1000 మి.లీ.
∴ 3 లీటర్లు = 3 × 1000 = 3000 మి.లీ.
200 మి.లీ.కు 3 లీటర్లు = 200 : 3000
= 2 : 30
= 1 : 15
![]()
ప్రశ్న 3.
100 గ్రాముల కాఫీ పొడి ధర ₹ 36. \(\frac {1}{2}\) కి.గ్రా. టీ పొడి ధర ₹ 240. అయిన కాఫీ పొడి మరియు టీపొడి ధరల నిష్పత్తి ఎంత?
సాధన.
ధరల నిష్పత్తిని కనుగొనాలంటే వాటి పరిమాణాలు సమానంగా ఉండాలి. కావున రెండింటిని 1 కి.గ్రా. ధరలను పరిగణనలోనికి తీసుకోవాలి.
1 కిలోగ్రాము = 1000 గ్రాములు = 10 × 100 గ్రాములు
100 గ్రాముల కాఫీ ధర = ₹ 36 రూపాయలు
∴ 1 కి.గ్రా. కాఫీ ధర = ₹ 36 × 10 = ₹360 రూపాయలు
\(\frac {1}{2}\) కి.గ్రా. టీ ధర = ₹240
∴ 1 కి.గ్రా. టీ ధర = 2 (240) = ₹ 480
ధరల నిష్పత్తి = 1 కి.గ్రా. కాఫీ ధర : 1 కి.గ్రా. టీ ధర
= 360 : 480
= 36 : 48
= 9 : 12
= 3 : 4
ప్రశ్న 4.
5 : 8 మరియు 2 : 9 లను సరిపోల్చండి.
సాధన.
నిష్పత్తులను భిన్న రూపంలో రాయగా, 5 : 8 = \(\frac {5}{8}\) మరియు 2 : 9 = \(\frac {2}{9}\)
8 మరియు 9 ల క.సా.గు ను కనుగొనండి. 8 × 9 = 72
పై రెండు భిన్నాల హారాలను 72 గా చేయగా

ప్రశ్న 5.
₹ 5,600 ను 3 : 4 నిష్పత్తిలో లలిత మరియు శేఖర్కు పంచండి.
సాధన.
ఇవ్వబడిన సొమ్ము = ₹ 5,600
ఇవ్వబడిన నిష్పత్తి = 3 : 4
నిష్పత్తి పదాల మొత్తం = 3 + 4 = 7
లలిత వాటా = \(\frac {3}{7}\) × 5,600 = 3 × 800 = ₹ 2,400
శేఖర్ వాటా = \(\frac {4}{7}\) × 5,600 = 4 × 800 = ₹ 3,200
ప్రశ్న 6.
6 : 15 నకు సమానమైన రెండు నిష్పత్తులను రాయండి.
సాధన.
ఇవ్వబడిన నిష్పత్తి = 6 : 15 = \(\frac {6}{15}\)
లవంలను 3 చే గుణించగా
\(\frac{6}{15}=\frac{6 \times 3}{15 \times 3}=\frac{18}{45}\) = 18 : 45
లవ, హారంలను 3 చే భాగించగా
\(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}=\frac{2}{5}\) = 2 : 5
18 : 45 మరియు 2 : 5 లు సమాన నిష్పత్తులగును.
![]()
ప్రశ్న 7.
కింది బాల యందు సరైన సంఖ్యతో పూరించండి.

సాధన.
i) బాక్స్ ల యందు సంఖ్య కోసం ముందుగా హారం 18 మరియు 36 ను పరిశీలించాలి.
18 × 2 = 36 అన్నది మనకు తెలుసు.
కావున, లవంను కూడా 2 చే గుణించాలి. అట్లు చేయగా 12 × 2 = 24 వచ్చును.
∴ మొదటి బాక్స్ లో 24 ఉంచాలి.
రెండవ బాక్స్ లో నిండడానికి ఈసారి లవంలను, 12 మరియు 2 లను పరిశీలించాలి.
12 ÷ 2 = 6
కావున ఈసారి హారం 18 ని 6 చే భాగిస్తే రెండవ బాక్స్ లో సంఖ్య లభిస్తుంది.
18 ÷ 6 = 3
∴ రెండవ బాక్స్ లో సంఖ్య 3.
ii)
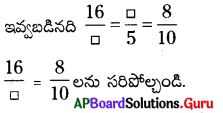
16 మరియు 8 లవములను పరిశీలించండి.
8ని 2 చే గుణిస్తే 16 వస్తుంది. 8 × 2 = 16
కావున 10 × 2 = 20 ని మొదటి బాలో ఉంచాలి.
రెండవ బాక్స్ లో నిండడానికి ఈసారి హారంలను, 5 మరియు 10 లను పరిశీలించాలి.
10 ÷ 5 = 2
కావున ఈసారి లవం 89.2 చే భాగిస్తే రెండవ బాక్స్ లో సంఖ్య లభిస్తుంది.
8 ÷ 2 = 4
∴ రెండవ బాక్స్ లో సంఖ్య = 4.
ప్రశ్న 8.
అనుపాతంలో ఉన్న కింది నిష్పత్తుల యందు ఖాళీలను పూరించండి.
![]()
సాధన.
ఇవ్వబడిన నిష్పత్తులు అనుపాతంలో ఉన్నవి కావున అంత్యముల లబ్ధం = మధ్యముల లబ్ధం.
అ) ఖాళీ యందు ఉంచవలసిన సంఖ్య = x అనుకొంటే అప్పుడు

15 × 57 = 19 × x లేదా 19x = 15 × 57
∴ x = \(\frac{15 \times 57}{19}\) = 15 × 3 = 45
∴ ఖాళీలో ఉంచాల్సిన సంఖ్య = 45
ఆ) ఖాళీలో ఉంచవలసిన సంఖ్య = y అనుకొంటే అప్పుడు
![]()
13 × 36 = y × 26
13×36 36 ..
∴ y = \(\frac{13 \times 36}{26}=\frac{36}{2}\) = 18
∴ ఖాళీలో ఉంచవలసిన సంఖ్య = 18
ప్రశ్న 9.
వెంకట్ 25 కి.గ్రా. బియ్యాన్ని ₹ 1200 లకు అమ్ముతున్నాడు. రహీమ్ 75 కి.గ్రా. బియ్యాన్ని ₹ 3,600 కు అమ్ముతున్నాడు. వారి రేట్ల నిష్పత్తి అనుపాతంలో ఉన్నాయా?
సాధన.
పద్ధతి-1 బరువుల నిష్పత్తి = 25 : 75 = 1 : 3
బియ్యం ధరల నిష్పత్తి = 1200 : 3600 = 12 : 36 = 1 : 3
నిష్పత్తులు రెండు సమానం కావున, అనుపాతంలో ఉన్నవి.
పద్ధతి-2 ఇచ్చట నిష్పత్తులు రెండూ 25 : 75 మరియు 1200 : 3600
అంత్యముల లబ్దం = 25 × 3600 = 90,000
మధ్యముల లబ్దం = 75 × 1200 = 90,000
అంత్యముల లబ్ధం = మధ్యముల లబ్ధంలో
25, 75, 1200, 3600 లు అనుపాతంలో ఉన్నవి.
![]()
ప్రశ్న 10.
డజను సబ్బుల ఖరీదు ₹ 306 లు, అయిన అటువంటి 15 సబ్బుల ఖరీదెంత?
సాధన.
1 డజను = 12 వస్తువులు
∴ 12 సబ్బుల ధర = ₹ 306
1 సబ్బు ధర = \(\frac {306}{12}\) = ₹25.50
15 సబ్బుల ధర = 15 × 25.50
= ₹ 382.50
ప్రశ్న 11.
24 పెన్సిళ్ల వెల₹ 72 అయిన 15 పెన్సిళ్ల వెల ఎంత ?
సాధన.
24 పెన్సిళ్ల వెల = ₹ 72
1 పెన్సిల్ వెల = \(\frac {72}{24}\) = ₹ 3
15 పెన్సిళ్ల వెల = 15 × 3 = ₹ 45/-
ప్రశ్న 12.
ఒక కారు 3\(\frac {1}{2}\) గంటలలో 175 కి.మీ. దూరం ప్రయాణిస్తుంది.
అ) 75 కి.మీ. దూరాన్ని అదే వేగంతో ఆ కారు ప్రయాణించడానికి ఎంత కాలం పడుతుంది ?
ఆ) ఆ కారు అంతే వేగంతో 2 గంటల కాలంలో ఎంత దూరం ప్రయాణిస్తుంది ?
సాధన.
175 కి.మీ. దూరాన్ని 3\(\frac {1}{2}\) గం॥ కాలంలో ప్రయాణించగలదు. అనగా 3\(\frac {1}{2}\) = \(\frac {7}{2}\) గం॥
అ) 175 కి.మీ. దూరం \(\frac {7}{2}\) గంటలలో ప్రయాణిస్తుంది.

∴ 75 కి.మీ. దూరాన్ని 1\(\frac {1}{2}\) గంటల కాలంలో ప్రయాణిస్తుంది.
ఆ) 3\(\frac {1}{2}\) గం॥ = \(\frac {7}{2}\) గం॥ కాలంలో ప్రయాణించిన దూరం = 175 కి.మీ.
2 గం॥ కాలంలో ప్రయాణించిన దూరం = \(\frac{2 \times 175}{\frac{7}{2}}\)
= \(\frac{2 \times 175 \times 2}{7}\)
= 2 × 25 × 2
= 100 కి.మీ.
2 గం॥ కాలంలో 100 కి.మీ. దూరం ప్రయాణించును.
ప్రశ్న 13.
కిందినీయబడిన వాటిని మిగిలిన రూపాలలో రాయండి.
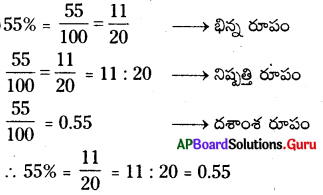
అ) 55%
ఆ) \(\frac {2}{25}\)
ఇ) 0.125 – ఈ) 37
సాధన.
అ)
ఆ) ఇవ్వబడిన సంఖ్య \(\frac {4}{25}\) భిన్న రూపంలో కలదు.
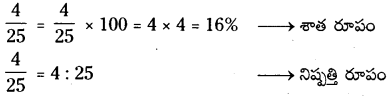

ఇ) ఇవ్వబడిన సంఖ్య 0.125 దశాంశ రూపం

ఈ) ఇవ్వబడిన సంఖ్య 3\(\frac {3}{4}\) భిన్న రూపం

ఉ) ఇవ్వబడిన .సంఖ్య 3 : 16 నిష్పత్తి రూపం
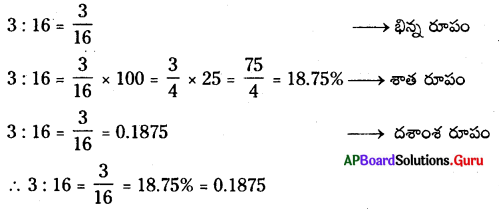
![]()
ప్రశ్న 14.
కనుక్కోండి.
అ) 25 కి.గ్రా.లో 24%
ఆ) ₹ 2400 లో 5\(\frac {1}{2}\) వ భాగం
సాధన.
y లో x% = \(\frac{\mathrm{x}}{100}\) × y అవుతుందని మనకు తెలుసు.
అ) 25 కి.గ్రా.లో 24% = \(\frac {24}{100}\) × 25 = \(\frac {24}{4}\) = 6 కి.గ్రా.
ఆ) ₹ 2400 లో 5\(\frac {1}{2}\) వ భాగం = \(\frac {11}{2}\) × \(\frac {1}{100}\) × 2400 = 11 × 12 = ₹ 132
ప్రశ్న 15.
4 రోజులలో 12 గంటలను శాత రూపంలో రాయండి.
సాధన.
1 రోజుకు = 24 గంటలు
4 రోజులకు = 4 × 24 = 96 గంటలు
4 రోజులలో x% = 12 గంటలు అనుకోండి.
⇒ 96 గంటలలో x% = 12 గంటలు అవుతుంది.
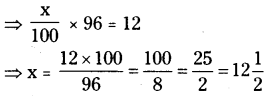
కావున 4 రోజులలో 12 గంటలు 12\(\frac {1}{2}\)% అవుతుంది.
ప్రశ్న 16.
వేమవరం గ్రామ జనాభాలో 60% స్త్రీలు. గ్రామ జనాభా 2,400 అయిన ఆ గ్రామంలో పురుషులెందరు?
సాధన.
వేమవరం గ్రామ జనాభా = 2,400 గా ఇవ్వబడింది.
60% జనాభా = \(\frac {60}{100}\) × 2,400 = 1,440
∴ స్త్రీల జనాభా = 1,440
పురుష జనాభా = మొత్తం జనాభా – స్త్రీల జనాభా
= 2,400 – 1,440 = 960
మరొక పద్ధతి :
వేమవరం జనాభా = 2,400
స్త్రీల జనాభా = 60%
మిగిలిన వారు పురుషులు కాబట్టి
100% – 60% = 40% పురుషులు
పురుషుల జనాభా = 2,400 లో 40% = \(\frac {40}{100}\) × 2,400 = 40 × 24 = 960
∴ వేమవరంలో పురుష జనాభా = 960