AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Ex 6.2 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Ex 6.2
Question 1.
Check whether the following are in proportion? or not?
(a) 10, 12, 15, 18
(b) 11, 16, 16, 21
(c) 8, 13, 17, 19
(d) 30, 24, 20, 16
Answer:
a) 10, 12, 15, 18
Given numbers are 10, 12, 15, 18.
If a, b, c, d are in proportion i.e., a : b :: c : d,
then product of extremes = product of means (a.d = b.c)
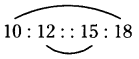
a : b :: c : d
10 × 18 = 12 × 15
180 = 180
If the product of extremes is equal to the product of means, then the given numbers are in proportion.
So, 10, 12, 15 and 18 are in proportion,
![]()
b) 11, 16, 16, 21
Given numbers are 11, 16, 16, 21.
If a, b, c, d are in proportion i.e., a : b :: c : d, then product of extremes = product of means (a.d = b.c)
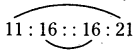
11 × 21 = 16 × 16
231 ≠ 256
Here the product of extremes is not equal to the product of means, then the given numbers are not in proportion.
So, 11,16, 16 and 21 are not in proportion.
c) 8, 13, 17, 19
Given numbers are 8, 13, 17,19.
If a, b, c, d are in proportion i.e., a : b :: c : d,
then the product of extremes = product of means (a.d = b.c)
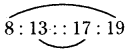
8 × 19 = 13 × 17
152 ≠ 221
Here the product of extremes is not equal to the product of means, then the given numbers are not in proportion.
So, 8,13, 17 and 19 are not in proportion.
d) 30, 24, 20, 16
Given numbers are 30, 24, 20, 16.
If a, b, c, d are in proportion i.e., a : b :: c : d,
then the product of extremes = product of means (a.d = b.c)
30 : 24 :: 20 : 16
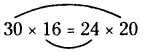
480 = 480
Here the product of extremes is equal to the product of means, then the given numbers are in proportion.
So, 30, 24, 20 and 16 are in proportion.
![]()
Question 2.
Write true or false for each of the following.
a) 4 : 2 :: 14 : 7
b) 21 : 7 :: 15 : 5
c) 13 : 12 :: 12 : 13
d) 5 : 6 :: 7 : 8
Answer:
a) 4 : 2 :: 14 : 7
Given proportion is 4 : 2 :: 14 : 7
If a, b, c, d are in proportion, then a.d = b.c
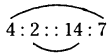
4 × 7 = 2 × 14
28 = 28
So, the given proportion is true.
b) 21 : 7 :: 15 : 5
Given proportion is 21 : 7 : : 15 : 5
If a, b, c, d are in proportion, then a.d = b.c
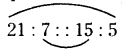
21 × 5 = 7 × 15
105 = 105
So, the given proportion is true.
c) 13 : 12 :: 12 : 13
Given proportion is 13 : 12 :: 12 : 13
If a, b, c, d are in proportion, then a.d = b.c
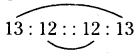
13 × 13 = 12 × 12
169 ≠ 144
So, the given proportion is false.
![]()
d) 5 : 6 :: 7 : 8
Given proportion is 5 : 6 :: 7 : 8
If a, b, c, d are in proportion, then a.d = b.c
![]()
5 × 8 = 6 × 7
40 ≠ 42
So, the given proportion is false.
Question 3.
Check whether the following form a proportion? Write middle terms and extremes where the ratios form a proportion.
a) 15 cm, 1 m and Rs. 45, Rs. 300
b) 20 ml, 2 l and Rs. 100, Rs. 10,000
Answer:
a) 15 cm, 1 m and Rs. 45, Rs. 300
Given values are 15 cm, 1 m and Rs. 45, Rs. 300
Ratio of lengths = 15 cm : 1 m (convert metres into cm)
= 15 cm : 100 cm = 3 : 20 (write in simplest form)
Ratio of amounts = Rs. 45 : Rs. 300 = 45 : 300 = 3 : 20
The two ratios are equal.
So, 3 : 20 :: 3 : 20 They are in proportion.
Middle terms are 20, 3 and extremes are 3, 20.
b) 20 ml, 2 l and Rs. 100, Rs. 10,000
Given values are 20 ml, 2 l and Rs. 100, Rs. 10,000
Ratio of quantities = 20 ml : 2 l (convert litres into ml)
= 20 : 2000 (write in simplest form)
= 1 : 100
Ratio of amounts = Rs. 100 : Rs. 10,000 (write in simplest form)
= 1 : 100
The two ratios are equal.
So, 1 : 100 = 1 : 100
∴ They are in proportion.
Middle terms are 100, 1 and extremes are 1, 100.
![]()
Question 4.
Find the missing numbers in the following proportions.
a) 8 : 12 :: ![]() : 48
: 48
b) 15 : ![]() :: 105 : 98
:: 105 : 98
c) 34 : 102 :: 27 : ![]()
Answer:
a) 8 : 12 :: ![]() : 48
: 48
Given proportion is 8 : 12 :: ![]() : 48
: 48
Let the missing number = x
If the given numbers are in proportion, then
Product of extremes = Product of means
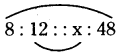
8 × 48 = 12 × x (or) 12x = 8 × 48
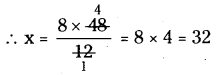
∴ Missing number in the proportion = 32
b) 15 : ![]() :: 105 : 98
:: 105 : 98
Given proportion is 15 : ![]() : 105 : 98
: 105 : 98
Let the missing number = a
If the given numbers are in proportion, then Product of extremes = product of means
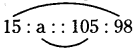
15 × 98 = 105 × a (or) 105 a = 15 × 98
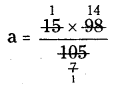
∴ a = 14
Missing number in the proportion
![]()
c) 34 : 102 :: 27 : ![]()
Given proportion is 34 : 102 :: 27 : ![]()
Let the missing number = y
If the given numbers are in proportion,
then the product of extremes = product of means

Missing number in the proportion = 81