AP State Syllabus AP Board 6th Class Maths Solutions Chapter 3 HCF and LCM Ex 3.1 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson HCF and LCM Ex 3.1
Question 1.
Which of the following numbers are divisible by 2, by 3 and by 6?
Answer:
i) 237192 has 2 in its one’s place.
The number which has 0, 2, 4, 6 and 8 in its ones place is divisible by 2.
237192 has 2 in its ones place. So, 237192 is divisible by 2.
(OR)
237192 is an even number and Hence divisible by 2.
Sum of the digits = 2 + 3 + 7 + 1 + 9 + 2 = 24 is a multiple of 3 of 237192.
If the sum of the digits of a number is a multiple of 3.
Then the number is divisible by 3.
So, 237192 is divisible by 3.
If a number is divisible by both 2 and 3, then it is also divisible by 6.
237192 is divisible by both 2 and 3.
Therefore 237192 is divisible by 6.
ii) 193272 has 2 in its ones place.
So, 193272 is divisible by 2.
[ Sum of the digits = 1 + 9 + 3 + 2 + 7 + 2 = 24 is a multiple of 3.
So, 193272 is divisible y 3.
193272 is divisible by both 2 and 3.
Therefore 193272 is divisible by 6.
iii) 972312 has 2 in its ones place.
So, 972312 is divisible by 2.
Sum of the digits = 9 + 7 + 2 + 3 + 1 + 2 = 24 is a multiple of 3
So, 972312 is divisible by 3.
972312 is divisible by both 2 and 3.
Therefore 972312 is divisible by 6.
![]()
iv) 1790184 has 4 in its ones place.
So, 1790184 is divisible by 2.
Sum of the digits = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30 is a multiple of 3.
So, 1790184 is divisible by 3.
1790184 is divisible by both 2 and 3.
Therefore 1790184 is divisible by 6.
v) 312792 has 2 in its ones place.
So, 312792 is divisible by 2.
Sum of the digits = 3 + 1 + 2 + 7 + 9 + 2 = 24 is a multiple of 3.
So, 312792 is divisible by 3.
312792 is divisible by both 2 and 3.
Therefore 312792 is divisible by 6.
vi) 800552 has 2 in its ones place.
So, 800552 is divisible by 2.
Sum of the digits = 8 + 0 + 0 + 5 + 5 + 2 = 20 is not a multiple of 3.
So, 800552 is not divisible by 3.
800552 is divisible by 2 but not by 3.
Therefore 800552 is not divisible by 6.
vii) 4335 has 5 in its ones place.
So, 4335 is not divisible by 2.
Sum of the digits = 4 + 3 + 3 + 5 = 15 is a multiple of 3.
So, 4335 is divisible by 3.
4335 is not divisible by 2 but it is divisible only by 3.
Therefore 4335 is not divisible by 6.
viii) 726352 has 2 in its ones place.
So, 726352 is divisible by 2.
Sum of the digits = 7 + 2 + 6 + 3 + 5 + 2 = 25 is not a multiple of 3.
So, 726352 is not divisible by 3.
726352 is divisible by 2 but not divisible by 3.
Therefore 726352 is not divisible by 6.
![]()
Question 2.
Determine which of the following numbers are divisible by 5 and by 10.
25, 125, 250, 1250, 10205, 70985, 45880.
Check whether the numbers that are divisible by 10 are divisible by 2 and 5.
Answer:
The numbers with zero or five at ones place are divisible by 5.
The numbers which have 0, 2, 4, 6 and 8 in its units place are divisible by 2.
The numbers with zero at ones place are divisible by 10.
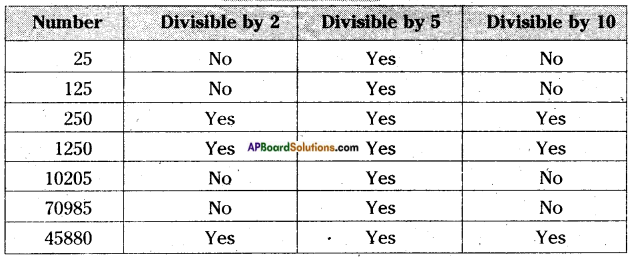
Therefore the numbers that are divisible by 10 are also divisible by both 2 and 5.
Question 3.
Make 3 different 3 digit numbers using 2, 3, 4 where each digit can be used only once, Check which of these numbers is divisible by 9.
Answer:
3 different 3-digit numbers using 2, 3, 4 are 234, 342, 243
Given digits 2, 3 & 4; their sum = 2 + 3 + 4 = 9,
Any number formed by these digits is always divisible by 9.
a) Sum of the digits of 234 = 2 + 3 + 4 = 9 is divisible by 9.
If the sum of the digits of the number is divisible by 9.
So, 234 is divisible by 9.
b) Sum of the digits of 342 = 3 + 4 + 2 = 9 is divisible by 9.
So, 342 is divisible by 9.
c) Sum of the digits of 243 = 2 + 4 + 3 = 9 is divisible by 9.
So, 243 is divisible by 9.
Question 4.
Write different 2 digit numbers using digits 5, 6, 7. Check whether these numbers are divisible by 2, 3, 5, 6 and 9.
Answer:
Different 2 digit numbers using 5, 6, 7 are 56, 57, 65, 67, 75, 76
56, 76 are divisible by 2
57, 75 are divisible by 3
65, 75 are divisible by 5
There is no number which is divisible by 6. [both 2 and 3 and there by 6]
There is no number which is divisible by 9.
![]()
Question 5.
Find the smallest number that must be added to 128, so that it becomes exactly divisible by 5.
Answer:
Given number be 128.
A number to be divisible by 5, its unit digit must be ‘0’ or ‘5’.
So, 128 + 2 = 130 is divisible by 5
128 + 7 = 135 is divisible by 5
In these two numbers, 2 is the smallest number.
The smallest number to be added is 2.
Question 6.
Find the smallest number that has to be subtracted from 276 so that it becomes exactly divisible by 10.
Answer:
Given number be 276.
A number to be divisible by 10, its units digit must be ‘0’.
So, 276 – 6 = 270 is divisible by 10.
276 – 16 = 260 is divisible by 10.
In these numbers, 6 is the smallest number.
∴ The smelliest number to be subtracted is 6.
Question 7.
Write all the numbers between 100 and 200 which are divisible by 6.
Answer:
The numbers in between 100 and 200 are
101, 102, 103, 104 ……. 198, 199
102 is divisible by 2 and 3. So 102 is divisible by 6.
Adding 6 to it successively we get
102, 108, 114, 120 126, 132, 138, 144, 150, 156, 162, 168, 174, 180, 186, 192, 198 are multiples of 6 and are divisible by 6.
![]()
Question 8.
Write the greatest four digit number which is divisible by 9. Is it divisible by 3? What do you notice?
Answer:
The greatest four digit number is 9999.
Sum of the digits of 9999 = 9 + 9 + 9 + 9 = 36 is divisible by 9
So, 9999 is divisible by 9.
Sum of the digits of 9999 is also multiple of 3.
Therefore, 9999 is also divisible by 3.
We notice that the numbers which are divisible by 9 are always divisible by 3.
Question 9.
Which of the following are divisible by 8?
(i) 1238
(ii) 13576
(iii) 93624
(iv) 67104
Answer:
i) 1238
The number formed by the last 3-digits is 238.

If the number formed by the last 3-digits in the same order is divisible by 8, then the number is divisible by 8.
238 is not divisible by 8. So, 1238 is not divisible by 8.
ii) 13576

The number formed by the last 3-digits is 576. 576 is divisible by 8. So, 13576 is divisible by 8.
iii) 93624

The number formed by the last 3-digits is 624. 624 is divisible by 8. So, 93624 is divisible by 8.
iv) 67104

The number formed by the last 3-digits is 104. 104 is divisible by 8. So, 67104 is divisible by 8.
![]()
Question 10.
Write the nearest number to 12345 which is divisible by 4.
Answer:
Given number be 12345.
A number to be divisible by 4, the number formed by the last two digits is divisible by 4.
So, 12345 – 1 = 12344 is divisible by 4
12345 – 2 = 12343 is not divisible by 4
12345 – 3 = 12342 is not divisible by 4
12345 – 4 = 12341 is not divisible by 4
12345 – 5 = 12340 is divisible by 4
and
12345 + 1 = 12346 is not divisible by 4
12345 + 2 = 12347 is not divisible by 4
12345 + 3 = 12348 is divisible by 4
12340, 12344 and 12348 are divisible by 4.
∴ 12344 is the nearest number to 12345 which is divisible by 4.