AP Board 10th Class Maths Solutions Chapter 8 సరూప త్రిభుజాలు Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Optional Exercise

ప్రశ్న 1.
ఇచ్చిన పటంలో, \(\frac{Q T}{P R}=\frac{Q R}{Q S}\) మరియు ∠1 = ∠2 అయిన ∆PQS ~ ∆TQR అని చూపండి.
సాధన.

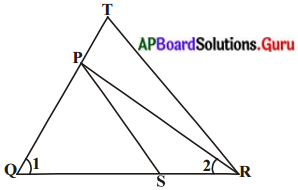
దత్తాంశము : \(\frac{Q T}{P R}=\frac{Q R}{Q S}\) మరియు ∠1 = ∠2
సారాంశము : ∆PQS ~ ∆TQR
ఉపపత్తి : ∆PQR లో ∠1 = ∠2 కావున PQ = PR .
[∵ సమాన కోణాల ఎదుటి భుజాలు సమానము)
∴ \(\frac{\mathrm{QT}}{\mathrm{PR}}=\frac{\mathrm{QR}}{\mathrm{QS}}\)
⇒ \(\frac{\mathrm{QT}}{\mathrm{PQ}}=\frac{\mathrm{QR}}{\mathrm{QS}}\)
∆TQR లో PS రేఖ మిగిలిన రెండు భుజాలు QT మరియు QR లను సమాన నిష్పత్తిలో విభజిస్తుంది. కావున PS || TR. [ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము]
∆PQS మరియు ∆TORలలో ∠QPS = ∠QTR
[∵ ∠P, ∠T లు ఆసన్నకోణాలు]
∠QSP = ∠QRT [PS || TR కావున ∠S, ∠Rలు ఆసన్న కోణాలు]
∠Q = ∠Q (ఉమ్మడి కోణము)
∴ ∆PQS ~ ∆TQR (కో.కో.కో సరూపకత నియమము నుండి).

ప్రశ్న 2.
రవి ఎత్తు 1.82 మీ. అతని ఇంటి పెరడులోని ఒక చెట్టు ఎత్తును తెలుసుకోవాలనుకున్నాడు. చెట్టు మొదలు నుండి నేలపై 12.20 మీటర్ల దూరము నడువగా అతని నీడ, చెట్టు నీడ చివరి భాగములు ఖచ్చితముగా ఏకీభవించినాయి. అతను ఇపుడు ఆ నీడ చివరి భాగము నుండి 6.10 మీ. దూరములో నిలబడి వున్నచో, ఆ చెట్టు ఎత్తు ఎంత ?

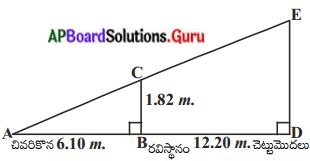
సాధన.
దత్తాంశము ప్రకారం, రవి ఎత్తు = BC = 1.82 మీ.
చెట్టు అడుగు నుండి రవి వద్దకు గల దూరము = BD = 12.2 మీ.
రవి నీడ పొడవు = BC = 6.10 మీ.
DE చెట్టును సూచిస్తుంది.
పటం నుండి ∆ABC ~ ∆ADE కావున \(\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{BC}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{AE}}\)
[సరూప త్రిభుజాల అనురూప భుజాల నిష్పత్తులు సమానము]
\(\frac{6.10}{6.10+12.20}=\frac{1.82}{\mathrm{DE}}\)
DE = \(\frac{1.82 \times 18.30}{6.10}\)
∴ చెట్టు యొక్క ఎత్తు = 5.46 మీ.

ప్రశ్న 3.
సమాంతర చతుర్భుజము ABCD లో, AB పై ” ఏదేని బిందువు ‘F’. దాని కర్ణము AC, DP ని బిందువు ( వద్ద ఖండించును. అయిన CQ × PQ = QA × QD అని చూపండి.
సాధన. ”

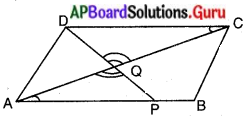
దత్తాంశము : ▱ ABCD ఒక సమాంతర చతుర్భుజం. AB పై P ఒక బిందువు. DP మరియు AC లు Q వద్ద ఖండించుకొనును.
సారాంశము : CQ · PQ = QA · QD.
ఉపపత్తి : ∆CQD, ∆AQP లలో ∠QCD = ∠QAP, ∠CQD = ∠AQP
∴∠ODC = ∠OPA (∵ త్రిభుజ కోణాల మొత్తం ధర్మం )
ఆ విధముగా ∆CQD ~ ∆AQP (కో-కో-కో సరూప నియమం నుండి)
∴ \(\frac{\mathrm{CQ}}{\mathrm{AQ}}=\frac{\mathrm{QD}}{\mathrm{QP}}=\frac{\mathrm{CD}}{\mathrm{AP}}\) [∵ సరూప త్రిభుజాల అనురూప భుజాల నిష్పత్తులు సమానము]
\(\frac{\mathrm{CQ}}{\mathrm{AQ}}=\frac{\mathrm{QD}}{\mathrm{QP}}\)
CQ . PQ = QA . QD [Q.E.D].

ప్రశ్న 4.
∆ABC మరియు ∆AMPలు రెండు లంబకోణ త్రిభుజములు. వీటిలో లంబకోణములు వరుసగా B మరియు M బిందువుల వద్ద కలవు. అయిన
(i) ∆ABC – ∆AMP
(ii) \(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\) అని చూపండి.

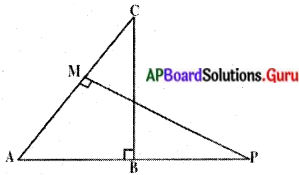
సాధన.
దత్తాంశము : ∆ABC; ∠B = 90°
∆AMP; ∠M = 90°
సారాంశము : (i) ∆ABC ~ ∆AMP
(ii) \(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\)
ఉపపత్తి : (i) ∆ABC మరియు ∆AMP లలో ∠B = ∠M [ప్రతి కోణం 90°] ∠A = ∠A [ఉమ్మడి కోణం]
కావున ∠C = ∠P [త్రిభుజ కోణాల మొత్తం ధర్మం నుండి]
∆ABC ~ ∆AMP (కో-కో-కో- సరూపకత నుండి)

(ii) ∆ABC ~ ∆AMP (నిరూపించబడినది)
\(\frac{\mathrm{AB}}{\mathrm{AM}}=\frac{\mathrm{BC}}{\mathrm{MP}}=\frac{\mathrm{CA}}{\mathrm{PA}}\) [సరూప త్రిభుజాల, అనురూప భుజాల నిష్పత్తులు సమానము]
∴ \(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\).

ప్రశ్న 5.
ఒక విమానము విమానాశ్రయము నుండి, గంటకు 1000 కి.మీ. వేగముతో ఉత్తరము వైపు ప్రయాణించు చున్నది. అదే సమయంలో వేరొక విమానము అక్కడి నుండి గంటకు 1200 కి.మీ. వేగముతో పడమర వైపు ప్రయాణించుచున్నది. అయిన 12 గంటల తరువాత ఆ రెండు విమానాల మధ్యదూరము ఎంత ?
సాధన.
దత్తాంశము : ఉత్తర దిశలో మొదటి విమాన వేగము = 1000 కి.మీ./గం.
పడమర దిశలో రెండవ విమాన వేగము = 1200 కి.మీ./గం.
దూరము = వేగము × కాలము
1\(\frac{1}{2}\) గం||లో మొదటి విమానము ప్రయాణించిన దూరము = 1000 × 1\(\frac{1}{2}\)
= 1000 × \(\frac{3}{2}\) = 1500 కి.మీ.
1\(\frac{1}{2}\) గం||లో రెండవ విమానము ప్రయాణించిన దూరము = 1200 × \(\frac{3}{2}\) = 1800 కి.మీ.

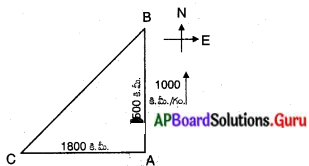
పటం నుండి ∆ABC ఒక లంబకోణ త్రిభుజము మరియు ∠A = 90°.
∴ AB² + AC² = BC² (పైథాగరస్ సిద్ధాంతం నుండి)
1500² + 1800² = BC²
BC² = 2250000 + 3240000
BC² = 5490000
BC = /5490000 = 100 × √549 m
= 100 × 23.43 = 2243కి.మీ.

ప్రశ్న 6.
లంబకోణ త్రిభుజము ABCలో లంబకోణము C వద్ద కలదు. P మరియు Q బిందువులు వరుసగా AC మరియు CB లపై బిందువులు ఇంకా ఆ భుజాలను అవి 2 : 1 నిష్పత్తిలో విభజించును. అయిన
(i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB² అని చూపండి.
సాధన.

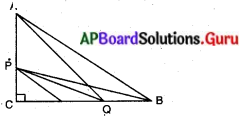
దత్తాంశము : ∆ABC లో ∠C = 90°
సారాంశము : (i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB²
ఉపపత్తి : ∆ACQ లో ∠C = 90° కావున AC² + CQ² = AQ² (పైథాగరస్ సిద్ధాంతం నుండి)
AQ² = AC² + (\(\frac{1}{2}\)BC)²
[BC ని Q బిందువు 2 : 1 నిష్పత్తిలో విభజిస్తుంది. CQ = \(\frac{2}{3}\) BC]
AQ² = AC² + \(\frac{4}{9}\) BC²
AQ² = \(\frac{9 A C^{2}+4 B C^{2}}{9}\)
⇒ 9AQ² = 9AC² + 4BC² ……… (i)
CA పై P బిందువు 2 : 1 నిష్పత్తిలో విభజించు విధముగా తీసుకున్నట్లయితే
BP² = PC² + BC²
BP² = (\(\frac{2}{3}\) AC)² + BC²
BP² = \(\frac{4}{9}\) AC² + BC²
BP² = \(\frac{4 \mathrm{AC}^{2}+9 \mathrm{BC}^{2}}{9}\)
9BP² = 4AC² + 9BC²

(ii) ∆PCB లో PB² = PC² + BC² [పైథాగరస్ సిద్ధాంతం నుండి)
PB² = (\(\frac{1}{3}\) AC)² + BC²
PB² = \(\frac{\mathrm{AC}^{2}}{9}\) + BC²
PB² = \(\frac{\mathrm{AC}^{2}+9 \mathrm{BC}^{2}}{9}\)
⇒ 9PB² = 9BC² + AC²

(iii) ∆ABC లో AC² + BC² = AB² [పైథాగరస్ సిద్ధాంతం నుండి]
(i) మరియు (ii) ల నుండి
9AQ² = 9AC² + 4BC²
9BP² = 9BC²+ 4AC² (కూడగా)
9AQ² + 9BP² = 13AC² + 13BC²
9 (AQ² + BP²) = 13 (AC² + BC²)
9 (AQ² + BP²) = 13 AB².