SCERT AP 10th Class Maths Textbook Solutions Chapter 3 బహుపదులు Optional Exercise Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 3rd Lesson బహుపదులు Optional Exercise
ప్రశ్న 1.
కింది ఘన బహుపదులకు ప్రక్కన ఇవ్వబడిన సంఖ్యలు ఆయా బహుపదులకు శూన్యాలు అగునో, లేదో సరిచూడండి ఇదే విధంగా బహుపదుల పదాల గుణకాలకు, శూన్యాలకు మధ్య గల సంబంధాన్ని రాబట్టండి.
(i) 2x3 + x2 – 5x + 2 ; (\(\frac{1}{2}\), 1, – 2)
(ii) x3 + 4x2 + 5x – 2 ; (1, 1, 1)
సాధన.
(i) 2x3 + x2 – 5x + 2, (\(\frac{1}{2}\), 1, – 2)
p(x) = 2x3 + x2 – 5x + 2
p(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\))3 + (\(\frac{1}{2}\))2 – 5(\(\frac{1}{2}\)) + 2
= \(\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+\frac{2}{1}\)
= \(\frac{1+1-10+8}{4}\)
p(\(\frac{1}{2}\)) = \(\frac{0}{4}\) = 0 …………… (1)
p(1) = 2(1)3 + (1)2 – 5(1) + 2 –
= 2 + 1 – 5 + 2
p(1) = 0 ……………… (2)
(లేదా)
p(x) లో గుణకాల మొత్తం 2 + 1 – 5 + 2 = 0
∴ p(1) = 0 ………… (2)
p(- 2) = 2(- 2)3+ (- 2)2 – 5(- 2) + 2
= 2(- 8) + 4 + 10 + 2
= – 16 + 16 = 0
p(- 2) = 0 ………………(3)
(1), (2) & (3) ల నుండి P(\(\frac{1}{2}\)) = 0
p(1) = 0
p(- 2) = 0
∴ p(x) కు \(\frac{1}{2}\), 1, – 2లు శూన్య విలువలు అవుతాయి.
α = \(\frac{1}{2}\), β = 1,γ = – 2 అనుకొందాం.
శూన్య విలువల మొత్తం α + β + γ = \(\frac{1}{2}\) + 1 + (- 2)
= \(\frac{3}{2}\) – 2
= \(-\frac{1}{2}\)
= 
రెండేసి శూన్య విలువల లబ్ధాల మొత్తం (αβ + βγ + γα) = (\(\frac{1}{2}\)) (1) + (1) (- 2) + (- 2) (\(\frac{1}{2}\))
= \(\frac{1}{2}\) – 2 – 1 = \(\frac{1}{2}\) – 3
= \(\frac{1-6}{2}=\frac{-5}{2}\) = 
శూన్య విలువల లబ్దం αβγ = \(\frac{1}{2}\) × 1 × (- 2)
= – 1 = 
![]()
(ii) x3 + 4x2 + 5x – 2, (1, 1, 1)
p(x) = x3 + 4x2 + 5x – 2
p(1) = (1)3 + 4(1)2 + 5(1) – 2
= 1 + 4 + 5 – 2
p(1) = 8
p(1) ≠ 0
∴ p(x) కు 1 శూన్య విలువ కాదు.
(లేదా)
గుణకాల మొత్తం = 0 అయితే 1 ఒక శూన్య విలువ అవుతుంది.
p(x) యొక్క గుణకాల మొత్తం 1 + 4 + 5 – 2 = 8
గుణకాల మొత్తం 8 ≠ 0.
∴ p(x) కు 1 శూన్య విలువ కాదు.
2వ పద్ధతి :
p(x) = x3 + 4x2 + 5x – 2 యొక్క శూన్య విలువలు α = β = γ = 1 అయితే p(x) = (x – 1)3 కావాలి.
(x – 1)3 = x3 – 3x2 + 3x – 1
p(x) = x3 + 4x2 + 5x – 2 ≠ (x – 1)3
∴ కాబట్టి 1, 1, 1లు p(x) యొక్క శూన్య విలువలు కావు.
![]()
ప్రశ్న 2.
ఒక ఘన బహుపది యొక్క శూన్యాల మొత్తము, రెండేసి శూన్యాల లబ్దాల మొత్తము మరియు శూన్యాల లబ్దము వరుసగా 2, – 7 మరియు – 14 అయిన ఆ బహుపదిని కనుగొనుము.
సాధన.
ఘన బహుపది p(x) యొక్క శూన్య విలువలు α, β, γ అనుకొనుము α + β + γ = 2
αβ + βγ + γα = – 7
αβγ = – 14
p(x) = k[x3 – (α + β + γ) x3 + (αβ + βγ + γα) x – αβγ]
= k[x3 – 2x2 + (- 7) x – (- 14)]
= k[x3 – 2x2 – 7x + 14]
k = 1 అయిన p(x) = x3 – 2x2 – 7x + 14.
![]()
ప్రశ్న 3.
x3 – 3x2 + x + 1 అను బహుపది శూన్యాలు a – b, a, a + b లు అయిన a, b విలువలను కనుగొనండి.
సాధన.
p(x) = x3 – 3x2 + x + 1 యొక్క శూన్య విలువలు α = a – b, β = a, γ = a + b –
శూన్య విలువల మొత్తం α + β + γ = 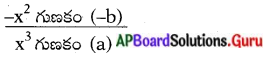
a – b + a + a + b = \(\frac{-(-3)}{1}\)
3a = 3
a = \(\frac{3}{3}\) = 1
శూన్య విలువల లబ్ధం αβγ = 
(a – b) (a) (a + b) = \(\frac{-1}{1}\)
కాని a = 1
∴ (1 – b) (1) (1 + b) = – 1
1 – b2 = – 1
-b2 = – 1 – 1 = – 2
b2 = 2
b = ± √2
∴ a = 1, b = ± √2.
![]()
ప్రశ్న 4.
x4 – 6x3 – 26x2 + 138x – 35 యొక్క రెండు శూన్యాలు 2 ± √3 అయిన మిగిలిన రెండు శూన్యాలను కనుగొనండి.
సాధన.
p(x) = x4 – 6x3 – 26x2 + 138x – 35 యొక్క రెండు శూన్య విలువలు 2 + √3 మరియు 2 – √3 . కాబట్టి
2 + √3 మరియు 2 – √3 శూన్య విలువలుగా గల వర్గ బహుపది p(x) కు కారణాంకం అవుతుంది.
α = 2 + √3 , β = 2 – √3 శూన్య విలువలుగా గల వర్గ బహుపది.
α + β = 2 + √3 + 2 – √3 = 4
αβ = 22 – (13)2 = 4 – 3 = 1.6
f(x) = k[x2 – (α + β) x + αβ]
= k [x2 – 4x + 1]
k = 1 ⇒ f(x) = x2 – 4x + 1,
p(x) కు కారణాంకము

భాగఫలంలో రెండవ పదం = \(\frac{x^{4}}{x^{2}}\) = x2
భాగఫలంలో మూడవ పదం = \(\frac{-2 x^{3}}{x^{2}}\) = – 2x
భాగఫలంలో మొదటి పదం = \(\frac{-35 x^{2}}{x^{2}}\) = x
![]()
బహుపదులు భాగహార అల్గారిథమ్ నుండి ,
p(x) = x4 + 6x3 – 26x2 + 138x – 35
⇒ (x2 – 4x + 1) (x2 – 2x – 35) + 0
p(x) = 0 అయిన
(x2 – 4x + 1) (x2 – 2x – 35) = 0
(x2 – 4x + 1) = 0 లేదా x2 – 2x – 35 = 0.
x2 – 4x + 1 యొక్క శూన్య విలువలు 2 + √3.
x2 – 2x – 35 యొక్క శూన్య విలువలు
x2 – 2x – 35 = 0
⇒ x2 – 7x + 5x – 35 = 0
x(x – 7) + 5 (x – 7) = 0
(x – 7) (x + 5) = 0
x – 7 = 0 లేదా x + 5 = 0.
x = 7 లేదా x = – 5
∴ p (x) యొక్క శూన్య విలువలు 2 + √3, 7 మరియు – 5.
![]()
ప్రశ్న 5.
x4 – 6x3 – 16x2 + 25x + 10 అనే బహుపదిని x2 – 2x + k అనే మరొక బహుపదిచే భాగించగా వచ్చు శేషం x + a అయిన ‘k’ మరియు ‘a’ విలువలు కనుగొనండి.
సాదన.
p(x) = x4 – 6x3 + 16x2 – 25x + 10
g(x) = x2 – 2x + k మరియు
r(x) = x + a

భాగఫలంలో మొదటి పదం = \(\frac{x^{4}}{x^{2}}\) = x2
భాగఫలంలో రెండవ పదం = \(\frac{-4 x^{3}}{x^{2}}\) = – 4x
భాగఫలంలో మూడవ పదం = \(\frac{-(24+k) x^{2}}{x^{2}}\) = – (24 + k)
శేషం r(x) = x + a
∴ (- 23 + 2k) x + (10 + 24k + k2) = x + a
x గుణకాలను పోల్చగా ,
– 23 + 2k = 1
2k = 24
∴ k = 12
స్థిర పదాలను పోల్చగా
![]()
2వ పద్ధతి :
(10 + 24k + k2)
p(x) = x4 – 6x3 – 16x2 + 25x + 10 లెక్క ప్రకారం
r(x) = x + 10
g(x) = x2 – 2x + k
భాగహార అల్ గారిథమ్ నుండి
p(x) = g(x) . q(x) + r(x)
p(x) – r(x) = g(x) . q(x)
p(x) – r(x) కు g(x) కారణాంకము అవుతుంది.
కాబట్టి p(x) – r(x) ను g(x) తో భాగిస్తే శేషము ‘0’ అవుతుంది.
కాని p(x) – r(x) a = (x4 – 6x3 – 16x2 + 25x + 10) – (x + a)
= x4 – 6x3 – 16x2 + 24x + (10 – a)

= [[24 + 4k) – (48 + 2k)] x + [(10 – a) + (24k + k)]
= (- 24 + 2k) x + (10 – a + 24k + k2) = 0 కావాలంటే
-24 + 2k = 0 మరియు 10 – a + 24k + k2 = 0 కావాలి
∴ 2k = 24 మరియు 10 – a + 24(12) + (12) = 0
k= 12 మరియు 10 – a + 288 + 144 = 0
442 – a = 0
∴ a = 442.
∴ k = 12 మరియు a = 442.
భాగఫలంలో మొదటి పదం = \(\frac{x^{4}}{x^{2}}\) = x
భాగఫలంలో రెండవ పదం = \(\frac{-4 x^{3}}{x^{2}}\) = – 4x
భాగఫలంలో మూడవ పదం = \(\frac{-(24+k) x^{2}}{x^{2}}\) = – (24+ k)