SCERT AP 10th Class Maths Textbook Solutions Chapter 12 త్రికోణమితి అనువర్తనాలు Optional Exercise Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 12th Lesson త్రికోణమితి అనువర్తనాలు Optional Exercise
ప్రశ్న 1.
1.2 మీటర్ల ఎత్తు గల బాలిక ఆకాశంలో క్షితిజ సమాంతరంగా, 88.2 మీటర్ల ఎత్తుతోపాటు గాలిలో ప్రయాణిస్తున్న బెలూనును 60° ఊర్ధ్వకోణంలో గమనించింది. కొంతకాలం తర్వాత ఆ ఊర్థ్వకోణం 300 గా మారింది. ఈ మధ్యకాలంలో బెలూను ప్రయాణించిన దూరం ఎంత ?
సాధన.
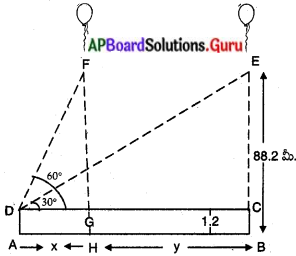
పటం నుండి,
AD = బాలిక ఎత్తు = 1.2 మీ.
FH = EB = 88.2 మీ. అనునది AB క్షితిజ సమాంతరం నుండి బెలూనుకు గల ఎత్తు D పరిశీలన బిందువు.
ఊర్వకోణములు ∠FDG = 60° మరియు ∠EDC = 30.
FG = EC = 88.2 – 1.2 = 87 మీ.
బెలూను ప్రయాణించిన దూరము, HB = y మీ. మరియు AH = x మీ.
∴ DG = x మీ. ‘ మరియు GC = y మీ. ,
∆FGD లో,
tan 60° = \(\frac{\mathrm{FG}}{\mathrm{DG}}\)
⇒ √3 = \(\frac{87}{x}\)
⇒ x = \(\frac{87}{\sqrt{3}}\) ……………… (1)
∆ECD లో,
tan 30° = \(\frac{E C}{D C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{87}{D G+G C}\)
⇒ x + y = 87√3 …………… (2)
సమీకరణం (2) లో (1) ను ప్రతిక్షేపించగా,
\(\frac{87}{\sqrt{3}}\) + y = 87√3
⇒ y = 87√3 – \(\frac{87}{\sqrt{3}}\)
⇒ y = 87(√3 – \(\frac{1}{\sqrt{3}}\))
⇒ y = \(87\left(\frac{3-1}{\sqrt{3}}\right)\)
⇒ y = \(\frac{87 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
⇒ y = \(\frac{87 \times 2 \sqrt{3}}{3}\)
⇒ y = 29 × 2√3 = 58√3 మీ.
∴ బెలూను ప్రయాణించిన దూరం = 58√3 మీ.
![]()
ప్రశ్న 2.
ఒక భవన పాదం నుండి ఎదురుగా నున్న టవరు పై భాగం 30° ఊర్ధ్వకోణం చేస్తుంది. టవరు పాదం నుండి భవనం పై భాగం 60° ఊర్ధ్వకోణం చేస్తుంది. వాటి ఎత్తులు ఏ నిష్పత్తిలో ఉంటాయి ?
సాధన.
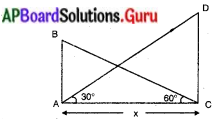
పటం నుండి, CD = టవరు ఎత్తు,
AB = భవనం ఎత్తు
AC = భవనంకు, టవరుకు మధ్యన గల దూరము
ఊర్ధ్వకోణములు ∠ACB = 60° మరియు ∠DAC = 30° ,
∆ABC నుండి,
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ √3 = \(\frac{\mathrm{AB}}{\mathrm{x}}\)
⇒ AB = √3x
∆ADC నుండి,
tan30° = \(\frac{\mathrm{CD}}{\mathrm{AC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{C D}{x}\)
⇒ CD = \(\frac{x}{\sqrt{3}}\) ……………… (2)
భవనం మరియు టవరుల యొక్క ఎత్తుల నిష్పత్తి .
AB : CD = √3x : \(\frac{x}{\sqrt{3}}\) = 3 : 1.
![]()
ప్రశ్న 3.
A, B మరియు C అను మూడు పడవలు ఒకే సరళరేఖలో ప్రయాణిస్తూ లైట్ హౌస్ వైపు వస్తున్నవి. ఆ పడవలలో నుండి లైట్ హౌస్ పై భాగాన్ని గమనించిన వరుసగా అవి a, 22 మరియు 3a ఊర్ద్వకోణాలను చేస్తున్నవి. A మరియు B పడవల మధ్య దూరం x అయిన ఆ లైట్ హౌస్ ఎత్తు ఎంత ?
సాధన.
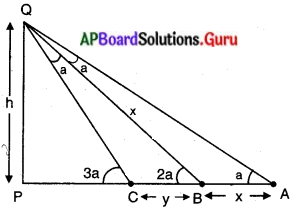
పటం నుండి,
PQ = లైట్ హౌస్ యొక్క ఎత్తు = h మీ.
A = మొదటి పరిశీలన బిందువు
B = రెండవ పరిశీలన బిందువు
C = మూడవ పరిశీలన బిందువు
AB = x మరియు BC = y (దత్తాంశములో ఇవ్వలేదు)
బాహ్యకోణము = అంతరాభిముఖ కోణాల మొత్తము
∠PBQ = ∠BQA + ∠BAQ మరియు
∠PCQ = ∠CBQ + ∠CQB
∴ AB = x = QB.
sine నియమమును అనుసరించి,

∆PBQ నుండి,
sin 2a = \(\frac{\mathrm{h}}{\mathrm{x}}\)
⇒ 2 sin a cos a = \(\frac{\mathrm{h}}{\mathrm{x}}\)
ఇరువైపులా వర్గం చేయగా,
⇒ 4 sin2 a cos2 a = \(\frac{h^{2}}{x^{2}}\)
⇒ 4 . \(\frac{3 y-x}{4 y} \cdot \frac{x+y}{4 y}=\frac{h^{2}}{x^{2}}\)
⇒ h2 = \(\frac{x^{2}}{4 y^{2}}(3 y-x)(x+y)\)
∴ h = \(\frac{x}{2 y} \sqrt{(3 y-x)(x+y)}\)
∴ లైట్ హౌస్ ఎత్తు = \(\frac{x}{2 y} \sqrt{(3 y-x)(x+y)}\)
![]()
ప్రశ్న 4.
ఒక దీర్ఘ ఘనాకారంలో ఉన్న గూడు లోపలి భాగంలో పొడవు, వెడల్పు మరియు ఎత్తుల నిష్పత్తి 1 : √2 : 1. ఆ గూటిలో పట్టు అతి పెద్ద కజ్ఞ, దాని భూమితో చేయు కోణం ఎంత ?
సాధన.
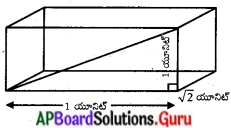
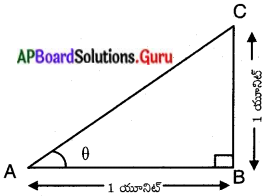
గూడు (Cup board) యొక్క అంతర భాగము దీర్ఘ ఘనాకృతిలో కలదు. ‘
పొడవు, వెడల్పు మరియు ఎత్తుల నిష్పత్తి 1 : √2 : 1
పటంలో, గూడు యొక్క పొడవు AB మరియు BC ఎత్తు అయిన AC అనునది దానిలో పట్టగల కర్ర
యొక్క గరిష్ఠ పొడవు అగును. కర్ర భూమితో చేయు కోణము ‘θ’ అనుకొనుము.
∆ABC లో,
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ tan θ = \(\frac{1}{1}\)
⇒ tan θ = tan 45°
θ = 45°
∴ గూటిలో పట్టు అతి పెద్ద కర్ర భూమితో చేయు కోణం 45°.
![]()
ప్రశ్న 5.
ఒక గోళాకార లోహపు బంతి ఘనపరిమాణం 232848 సెం.మీ. దానిని కరిగించి 120° లు శీర్షకోణము చేయు శంఖువు ఆకారంలో పోతపోశారు. అయిన దాని భూవ్యాసార్ధం, ఎత్తులను కనుగొనుము.
సాధన.

AC = ఏటవాలు ఎత్తు = l
AB = నిలువు ఎత్తు = h
BC = భూ వ్యాసార్థం = r
గోళాకార లోహపు బంతి ఘనపరిమాణం = 232848 cm3
లెక్క ప్రకారము గోళాకార లోహపు బంతి ఘనపరిమాణం = శంఖువు ఘనపరిమాణము
∴ \(\frac{1}{3}\) πr2h = 232848
∆ABC లో tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
√3 = \(\frac{r}{h}\)
⇒ r = √3h
\(\frac{1}{3}\)π(√3h)2 × h = 232848
\(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × h2 × h = 232848
h3 = \(\frac{232848 \times 7}{22}\)
h3 = 10584 × 7 = 74088
h3 = 423
⇒ h = 42, కాని r = h√3
⇒ r = 42√3