SCERT AP 10th Class Maths Textbook Solutions Chapter 11 త్రికోణమితి Exercise 11.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 11th Lesson త్రికోణమితి Exercise 11.2
ప్రశ్న 1.
క్రింది వాటి విలువలను కనుగొనండి.
(i) sin 45° + cos 45°
సాధన.
sin 45° + cos 45°
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{1+1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\frac{\sqrt{2} \times \sqrt{2}}{\sqrt{2}}\)
= √2
(ii) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 60^{\circ}}\)
సాధన.
\(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 60^{\circ}}=\frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}}+\frac{2}{\sqrt{3}}}\)
= \(=\frac{\frac{1}{\sqrt{2}}}{\frac{2+2}{\sqrt{3}}}=\frac{\frac{1}{\sqrt{2}}}{\frac{4}{\sqrt{3}}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4 \sqrt{2}}\)
![]()
(iii) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\cot 45^{\circ}+\cos 60^{\circ}-\sec 30^{\circ}}\)
సాధన.
\(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\cot 45^{\circ}+\cos 60^{\circ}-\sec 30^{\circ}}\)

(iv) 2 tan245° + cos230° – sin260°
సాధన.
2 tan245° + cos230° – sin260°
= 2(1)2 + \(\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{\sqrt{3}}{2}\right)^{2}\)
= \(\frac{2}{1}+\frac{3}{4}-\frac{3}{4}\) = 2
(v) \(\frac{\sec ^{2} 60^{\circ}-\tan ^{2} 60^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
సాధన.
\(\frac{\sec ^{2} 60^{\circ}-\tan ^{2} 60^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
= \(\frac{(2)^{2}-(\sqrt{3})^{2}}{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}=\frac{4-3}{\frac{1}{4}+\frac{3}{4}}=\frac{1}{\frac{1+3}{4}}=\frac{1}{\frac{4}{4}}=\frac{1}{1}\) = 1.
![]()
ప్రశ్న 2.
సరైన సమాధానాన్ని ఎంచుకొని, గుర్తించండి.
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
(a) sin 60°
(b) cos 60°
(c) tan 30°
(d) sin 30°
సాధన.
(c) tan 30°
= \(\frac{\frac{2}{\sqrt{3}}}{1+1}=\frac{2}{\sqrt{3}} \times \frac{1}{2}=\frac{1}{\sqrt{3}}\) = tan 30°
(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
(a) tan 90°
(b) 1
(c) sin 45°
(d) 0
సాధన.
(d) 0
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=\frac{1-(1)^{2}}{1+(1)^{2}}=\frac{1-1}{1+1}=\frac{0}{2}\) = 0.
![]()
(iii) \(\)
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
సాధన.
(c) tan 60°
\(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1-\left(\frac{1}{\sqrt{3}}\right)^{2}}=\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}\)
= \(\frac{\frac{2}{\sqrt{3}}}{\frac{3-1}{3}}=\frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{2}=\frac{3}{\sqrt{3}}\)
= \(\frac{\sqrt{3} \times \sqrt{3}}{\sqrt{3}}=\sqrt{3}\)
= tan 60°
ప్రశ్న 3.
sin 60° cos 30° + sin 30° cos 60° విలువను గణించండి. sin (60° + 30°) విలువ ఎంత?దీని నుండి మీరేం గ్రహించారు?
సాధన.
sin 60° cos 30° + sin 30° cos 60° = \(\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}+\frac{1}{2} \cdot \frac{1}{2}\)
= \(\frac{(\sqrt{3})^{2}}{4}+\frac{1}{4}\)
= \(\frac{3}{4}+\frac{1}{4}=\frac{4}{4}\) = 1 …………….. (1)
sin (60° + 30°) = sin 90° = 1 …….. (2)
(1), (2) నుండి
sin (60°+30°) = sin 60° . cos 30° + sin 30°. cos 60°.
sin (A + B) = sin A. cos B + cos A. sin B
![]()
ప్రశ్న 4.
cos (60° + 30°) = cos 60° cos 30° – sin 60° sin 30° అనడం సబబేనా ?
సాధన.
L.H.S. = cos (60° + 30°) = cos 90° = 0
R.H.S. = cos 60° . cos 30° – sin 60°. sin 30°
= \(\frac{1}{2} \cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \cdot \frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\) = 0
∴ L.H.S. = R.H.S.
∴ cos (60°+30°) = cos 60°. cos 30° – sin 60°. sin 30° అనవచ్చును
దీని నుండి cos (A + B) = cos A. cos B – sin A. sin B
ప్రశ్న 5.
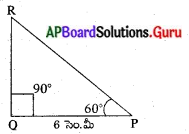
Qవద్ద లంబకోణం కల్గిన ∆PQRలో PQ = 6 సెం.మీ. ∠RPQ = 60° అయిన OR మరియు PR విలువలను కనుక్కోండి.
సాధన.
∆PQR లో Q వద్ద ‘లంబకోణము కలదు మరియు
PQ = 6 సెం.మీ., ∠RPQ = 60°.
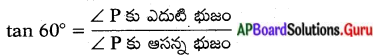
√3 = \(\frac{\mathrm{RQ}}{6}\)
RQ = 6√3 సెం.మీ.
PR భుజము పొడవు కనుగొనుటకు,
sin 60° = \(\frac{\mathrm{RQ}}{\mathrm{RP}}\)
\(\frac{\sqrt{3}}{2}=\frac{6 \sqrt{3}}{R P}\)
RP = 6√3 × \(\frac{2}{\sqrt{3}}\)
RP = 12 సెం.మీ. ……………… (2)
∴ QR పొడవు 6√3 సెం.మీ. మరియు RP పొడవు 12 సెం.మీ.
![]()
ప్రశ్న 6.
Y వద్ద లంబకోణం కల్గిన ∆XYZ లో YZ = x, మరియు ZX = 2x అయిన ∠YXZ మరియు ∠YZX ల విలువలను నిర్ణయించుము.
సాధన.
∆XYZ, Y వద్ద లంబకోణం కల్గిన ZX = 2x మరియు YZ = X అగును.
పైథాగరస్ సిద్ధాంతం ప్రకారం
XZ2 = XY2 + YZ2
(2x)2 = XY2 + (x)2
4x2 = XY2 + x2
XY2 = 4x2 – x2 = 3x2
XY = √(3x2) = √3x
∆XYZ నుండి
tan x = \(\frac{\mathrm{YZ}}{\mathrm{XY}}=\frac{\mathrm{x}}{\sqrt{3} \mathrm{x}}=\frac{1}{\sqrt{3}}\)
∴ tan 30 = \(\frac{1}{\sqrt{3}}\)
∴ ∠YXZ = 30
tan z = \(\frac{X Y}{Y Z}=\frac{\sqrt{3} x}{x}\) = √3
tan Z = √3 = tan 60°
∠Z = 60°
∴ ∆YXZ మరియు ∆YZXల విలువలు వరుసగా 30° మరియు 60.
![]()
ప్రశ్న 7.
sin (A + B) = sin A + sin B అనడం సబబేనా? మీ సమాధానాన్ని సమర్థించుము.
సాధన.
A = 30° మరియు B = 60° అనుకొనుము.
L.H.S. = sin (A + B)
= sin (30° + 60°) = sin 90° = 1
R.H.S. = sin 30° + sin 60°
= \(\frac{1}{2}+\frac{\sqrt{3}}{2}=\frac{\sqrt{3}+1}{2}\)
L.H.S. # R.H.S.
∴ sin (A + B) = sin A + sin B అనడం సబబు కాదు.