AP 10th Class Maths Bits Chapter 4 Pair of Linear Equations in Two Variables with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 4 Pair of Linear Equations in Two Variables on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 4th Lesson Pair of Linear Equations in Two Variables with Answers

Question 1.
The slope of the line passing through (2, 3) and (4, 7) is ………………….
A) 2
B) \(\frac{5}{6}\)
C) 4
D) 1
Answer:
A) 2

Question 2.
The value of P for which the pair of equations 2Px + 3y = 7, 2x + y = 6 has exactly one solution.
A) 3
B) Any real number except 3
C) Any real number
D) For no real P the system has solution
Answer:
B) Any real number except 3

Question 3.
If 2^x + 3^y = 17; 2^{x + 2} – 3^{y +1} = 5, then (x, y) is…………………..
A) (3, 2)
B) (2, 3)
C) (-2, 3)
D) (3, -2)
Answer:
A) (3, 2)

Question 4.
The value of k for which the system of equations (3k + 1) x + 3y – 2 = 0 and (k² + 1) x + (k – 2) y – 5 = 0 has no solution is…………………
A) 1
B) 2
C) -1
D) -2
Answer:
C) -1

Question 5.
The solution of the equations \(\frac{x+y}{x y}\) = 2 and \(\left\{2, \frac{-1}{4}\right\}\) = 6 is …………………..
A) \(\left\{\frac{-1}{2}, 4\right\}\)
B) \(\left\{2, \frac{-1}{4}\right\}\)
C) \(\left\{\frac{-1}{2}, \frac{-1}{4}\right\}\)
D) \(\left\{\frac{-1}{2}, \frac{1}{4}\right\}\)
Answer:
D) \(\left\{\frac{-1}{2}, \frac{1}{4}\right\}\)

Question 6.
The larger of two supplementary angles exceeds the smaller by 18°. The angles are ………………..
A) 80°, 100°
B) 81°, 99°
C) 82°, 98°
D) 83°, 97°
Answer:
B) 81°, 99°

Question 7.
If \(\) = 2 and \(\) = – 1,then ………………..
A) x = 2, y = 3
B) x = 4, y = 9
C) x = 2, y = 9
D) x = 4, y = 3
Answer:
B) x = 4, y = 9

Question 8.
The value of k for which the pair of equations 3x + 4y + 2 = 0 and 9x + 12y + k = 0 represent coincident lines is ……………..
A) 2
B) 3
C) 6
D) 12
Answer:
C) 6

Question 9.
If 2^x + 3^y = 31, 2^{x + 2} – 3^{y + 1} = 5, then …………………
A) x = 3, y = 2
B) x = 3,y = 4
C) x = 2, y = 3
D) x = 4, y = 3
Answer:
C) x = 2, y = 3

Question 10.
The point of intersection of the lines 2x + 3y – 5 = 0 and 3x – 4y + 1=0 lies in which quadrant ?
A) I
B) II
C) III
D) IV
Answer:
A) I

Question 11.
If the perimeter of a rectangular room is 34 and the length of the diagonal is 13, then the dimensions of the room are …………………
A) 7, 6
B) 11, 6
C) 12, 5
D) 12, 6
Answer:
C) 12, 5

Question 12.
If 9x + 11y = 51 and 11x + 9y = 49, then x = …………………….
A) -1
B) -2
C) 1
D) 2
Answer:
D) 2

Question 13.
If the pair of equations a₁x + b₁y + c₁= 0 and a₂ x + b₂y + c₂ = 0 has unique solution, then ………………
A) \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\)
B) \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
C) \(\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
D) \(\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Answer:
B) \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)

Question 14.
The solution of the equations √3x – √7y = 0 and √8x + √3y = 0 is ……………………
A) x = 3, y = 7
B) x = 8, y = 3
C) x = 0, y = 1
D) x = 0, y = 0
Answer:
D) x = 0, y = 0

Question 15.
If twice the age of A is added to B’s age, the sum is 45 and if twice the age of B is added to A’s age, the sum is 30. Then the age of B is ………………
A) 20
B) 5
C) 10
D) 30
Answer:
B) 5

Question 16.
3 pens and 5 pencils together cost ₹ 35, whereas 5 pens and 3 pencils together cost ₹ 37. The cost of a pencil is …………………
A) ₹ 5
B) ₹ 3
C) ₹ 4
D) ₹ 6
Answer:
C) ₹ 4

Question 17.
Which of the following is a solution for the equation 2(x + 3) = 18 ?
A) 6
B) 5
C) 21
D) 13
Answer:
A) 6

Question 18.
If 3x + 4y – k = 0 and 6x + 8y – 4 = 0 are coincident lines, then the value of k is ………………
A) 3
B) 4
C) 6
D) 2
Answer:
D) 2

Question 19.
If y = 3, then the value of ‘x’ satisfying the equation \(\frac{5}{x}+\frac{3}{y}\) = 6 is ……………….
A) 3
B) \(\frac{1}{3}\)
C) \(-\frac{1}{3}\)
D) 1
Answer:
D) 1

Question 20.
Which one of the following is NOT a linear equation?
A) 5x + 4 = y + 3
B) x + 2y = y² – x
C) 3 – x = y² + 4
D) x + y = 0
Answer:
C) 3 – x = y² + 4

Question 21.
“Book” is an example of ……………….
A) prism
B) circle
C) cone
D) cuboid
Answer:
D) cuboid

Question 22.
The value of x which satisfies the equation 2x – (4 – x) = 5 – x is …………………..
A) 4.5
B) 3
C) 2.25
D) 0.5
Answer:
C) 2.25

Question 23.
If \(\frac{10}{x+y}+\frac{2}{x-y}\) = 4 and \(\frac{15}{x+y}-\frac{5}{x-y}\) = -2 then
A) x = 3, y = 2
B) x = 3, y = -2
C) x = -3, y = 2
D) x = -3, y = -2
Answer:
A) x = 3, y = 2

Question 24.
The point of intersection of the lines x = 2016 and y = 2017 is …………………
A) (2017, 2016)
B) (0, 2017)
C) (2016, 0)
D) (2016, 2017)
Answer:
D) (2016, 2017)

Question 25.
Which of the following equations has the solution of (2, -3) ?
A) 2x – 3y = 10
B) 2x + 3y = -13
C) 2x – 3y = 13
D) 2x + 3y = 13
Answer:
C) 2x – 3y = 13

Question 26.
The point of intersection of the line y = ax + b with X – axis is ……………………
A) \(\left(-\frac{b}{a}, 0\right)\)
B) \(\left(\frac{\mathrm{b}}{\mathrm{a}}, 0\right)\)
C) \(\left(0, \frac{\mathrm{b}}{\mathrm{a}}\right)\)
D) \(\left(0,-\frac{\mathrm{b}}{\mathrm{a}}\right)\)
Answer:
A) \(\left(-\frac{b}{a}, 0\right)\)

Question 27.
The value of x, which satisfies 2(x – 1) – (1 – x) = 2x + 3 is ………………..
A) 2
B) 4
C) 6
D) 8
Answer:
C) 6

Question 28.
The value of y when \(\frac{x+y}{x y}\) = 2, \(\frac{x-y}{x y}\) = 6 is …………………
A) \(\frac{1}{4}\)
B) \(\frac{-1}{2}\)
C) \(\frac{-1}{4}\)
D) \(\frac{1}{3}\)
Answer:
A) \(\frac{1}{4}\)

Question 29.
Which of the following is inconsistent equation to 2x + 3y – 5 = 0 ?
A) 4x – 6y – 11 = 0
B) 2x + y = 5
C) x + 3y = 5
D) 4x + 6y – 11 = 0
Answer:
D) 4x + 6y – 11 = 0

Question 30.
Which of the following is not a linear equation ?
A) 5 + 4x = y + 3
B) x + 2y = y – x
C) 3 – x = y² + 4
D) x + y = 0
Answer:
C) 3 – x = y² + 4

Question 31.
The solution set {x, y} of the system of equations x – 2y = 0 and 3x + 4y = 10 is
A) {2, 4}
B) {4, 2}
C) {1, 2}
D){2, 1}
Answer:
D){2, 1}

Question 32.
The two lines 3x + 2y – 80 = 0 and 4x + 3y -110 = 0 are
A) coincident lines
B) parallel lines
C) intersecting lines
D) None
Answer:
C) intersecting lines

Question 33.
The perimeter of a rectangular plot is 32 m. If the length l is increased by 2 m and the breadth b is decreased by 1m, the area of the plot remains the same. Then the values of l and b are respectively.
A) 6m, 10m
B) 10m, 6m
C) 10m, 10m
D) 6m, 6m
Answer:
B) 10m, 6m

Question 34.
Which of the following equations is a linear equation ?
A) 5 + 4x² = y + 3
B)x + 2y = y² – x
C) 3 – x = y + 4
D) x² + y = 0
Answer:
C) 3 – x = y + 4

Question 35.
4y² – 5y + 1 is ……………………
A) Linear polynomial.
B) Cubic polynomial.
C) Constant polynomial.
D) Quadratic polynomial.
Answer:
D) Quadratic polynomial.

Question 36.
Which of the following is a linear equation ?
A) 5 + 4x = y + 3
B) x + 2y = y – x²
C) 3 – x = y² + 4
D) x² + y = 0
Answer:
A) 5 + 4x = y + 3

Question 37.
Solution for the equations √8 x + √7 y = 0 and √6 x + √10 y = 0 is …………………
A) x = 3, y = 5
B) x = 7, y = 11
C) x = 1, y = 1
D) x = 0, y = 0
Answer:
D) x = 0, y = 0

Question 38.
If the system of equations 4x + py = 21 and px – 2y = 15 has unique solution, then which of the following could be the value of p ?
a) 103
b) 105
c) 192
d) 197
A) Both (a) and (b)
B) Both (c) and (d)
C) (a), (b) and (d)
D) All of the above
Answer:
D) All of the above

Question 39.
The semi perimeter of a triangle exceeds each of its side by 5, 3 and 2 respectively. What is the perimeter of the triangle?
A) 10
B) 20
C) 15
D) 12
Answer:
B) 20

Question 40.
For what value of k do the equation 3(k – 1) x + 4y = 24 and 15x + 20y = 8 (k + 13) have infinite solutions ?
A) 4
B) 2
C) 1
D) 3
Answer:
B) 2

Question 41.
If the system of equations 2x – 3y = 3 and – 4x + qy = p is inconsistent, which of the following cannot be the value of p?
A) -36
B) -18
C) -24
D) -12
Answer:
D) -12

Question 42.
If 173x + 197y = 149 and 197x + 173y = 221, then find (x,y)
A) (2, -1)
B) (2, 1)
C) (-2, -1)
D)(-2, 1)
Answer:
A) (2, -1)

Question 43.
If an ordered pair satisfying the equations 2x – 3y = 18 and 4x – y = 16 also satisfies the equation 5x-py-23 = 0, then find the value of ‘p’.
A) 2
B) 5
C) 4
D) 1
Answer:
A) 2

Question 44.
In a fraction, if the numerator is decreased by 1 and the denominator is increased by 1. Then the fraction 1 becomes \(\frac {1}{2}\). Instead, if the numerator is increased by 1 and the denominator is decreased by 1. Then the fraction 4 becomes \(\frac {4}{5}\). Find the numerator of the fraction.
A) 2
B) 7
C) 4
D) 10
Answer:
B) 7

Question 45.
If a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 re such that a₁, b₁, c₁ a₂ b₂ and c₂ are consecutive integers in the same order then find the values of x and y.
A) -1, -2
B) 1, -2
C) -1, 2
D) 1, 2
Answer:
B) 1, -2

Question 46.
If the ordered pair (sinθ, cosθ) satisfies the system of equations
mx + ny + a + b = a-b and tvx + my + 2b = 0, then find the value of ‘θ’ where 0 ≤ θ ≤, 90° (m ≠ n)
A) 50°
B) 45°
C) 90°
D) 30°
Answer:
B) 45°

Question 47.
If we increase the length by 2 units and the breadth by 2 units, then the area of rectangle is increased by 54 square units. Find the perimeter of the rectangle (in units).
A) 50
B) 60
C) 58
D) 68
Answer:
A) 50

Question 48.
A two-digit number is formed by either subtracting 17 from nine times the sum of the digits or by adding 21 to 13 times the difference of the digits. Find the number.
A) 73
B) 79
C) 81
D) 92
Answer:
A) 73

Question 49.
If 3|x| + 5|y| = 8 and 7|x| — 3|y| = 48, then find the value of x + y.
A) -5
B) 5
C) -4
D) The value does not exist
Answer:
D) The value does not exist

Question 50.
A, B, C and D share a certain amount amongst themselves. 6 sees that the other three get 3 times what he himself gets C sees that the other three get 4 times what he gets, while D sees that the other three get 5 times what he gets. If the sum of the largest and smallest shares is 99, then what is the sum of the other two shares ?
A) 81
B) 62
C) 92
D) 78
Answer:
A) 81

Question 51.
The total cost of six books, five pencils and seven sharpeners is Rs. 115 and that of eight books, ten pencils and fourteen sharpeners is Rs. 190. Then which of the following article’s cost can be found uniquely
A) Pencil
B) Book
C) Sharpener
D) Cannot say
Answer:
B) Book

Question 52.
Swathi starts her job with certain monthly salary and earns a fixed increment every year. If her salary was Rs. 22500 per month after 6 years of service as Rs. 30000 per month after 11 years of service. Find her salary after 8 years of service (in Rs.).
A) 25500
B) 29500
C) 25000
D) 22343
Answer:
A) 25500

Question 53.
If a fraction becomes 2 when 9 is added to its numerator and 1 when 2 is subtracted from its denominator then the fraction is ………………….
A) \(\frac{6}{8}\)
B) \(\frac{7}{9}\)
C) \(\frac{5}{7}\)
D) \(\frac{4}{7}\)
Answer:
C) \(\frac{5}{7}\)

Question 54.
The values of ‘x’ and ‘y’ if \(\frac{5}{y}-\frac{2}{x}=\frac{7}{6}\) and \(\frac{36}{x}-\frac{24}{y}\) = 1 is …………………..
A) x = 4, y = 3
B) x = -4, y = 3
C) x = -4, y = -3
D) x = 4, y = -3
Answer:
A) x = 4, y = 3

Question 55.
A certain number of two digits is four times the sum of the digits. If 9 is added to the number the digits in the number are reversed, then the number is …………………
A) 13
B) 23
C) 12
D) 14
Answer:
C) 12

Question 56.
Six years ago a man was three times as old as his son. In 6 year’s time, he will be twice as old as his son. Then their present ages are
A) 30, 15
B) 40, 20
C) 42, 18
D) 41, 19
Answer:
C) 42, 18

Question 57.
The total salary of 15 men and 8 women is Rs. 3050. The difference of salaries of 5 women and 3 men is Rs. 50. The sum of the salaries of 3 men and 3 women is …………………
A) Rs. 900
B) Rs. 850
C) Rs. 750
D) Rs. 1000
Answer:
B) Rs. 850

Question 58.
If the sum of two numbers is 41 and their product is 400. Then the numbers are ………………
A) 40, 10
B) 20, 20
C) 25, 16
D) 28, 13
Answer:
C) 25, 16

Question 59.
A is twice as old as B, ten years ago. If A was four times as old as B, their present ages are ………………….
A) 24 and 12
B) 30 and 15
C) 32 and 16
D) 20 and 10
Answer:
B) 30 and 15

Question 60.
If one quarter of the sum of two numbers 1 is 14\(\frac {1}{2}\), their difference is 5, then the numbers are ………………….
A) 23, 30
B) 33, 45
C) 23, 33
D) 25, 35
Answer:
C) 23, 33

Question 61.
If x = 2p – 3q, y = p + 2q and z = q – 3p then x² + y² + z² + 2yz + 2zx + 2xy is …………………..
A) 0
B) 1
C) xyz
D) pqr
Answer:
A) 0

Question 62.
The sum of the digits of a two-digit number is 5. If the digit obtained by increasing the digit in ten’s place by unity is one-eighth of the number, then the number is ……………….
A) less than 30
B) lies between 30 and 40
C) more than 37
D) lies between 40 and 50
Answer:
B) lies between 30 and 40

Question 63.
There is a group of cows and chickens. If the number of legs was 14 more than twice the number of heads, then the number of cows is ……………………
A) 5
B) 8
C) 7
D) 4
Answer:
C) 7

Question 64.
If a + b + c = 0 then the value of \(\) is
A) 0
B) 1
C) 2
D) 3
Answer:
D) 3

Question 65.
The middle digit of number between 100 and 1000 is zero and the sum of the other digits is 11. If the digits are reversed, the number so formed exceeds the original number by 495, then the number is ………………..
A) 405
B) 408
C) 308
D) 309
Answer:
C) 308

Question 66.
A labourer was engaged for 30 days on the condition that he will be paid Rs. 35 for each day he works and will be fined Rs. 10 for each day he is absent. If he earned Rs. 735 in total, then the number of days he worked is ……………………….
A) 21
B) 22
C) 25
D) 23
Answer:
D) 23

Question 67.
For what value of k, the system of equations x + 2y = 3, 5x + ky + 7 = 0 has unique solution ?
A) k = 10
B) All real values except 10
C) All natural numbers except 10
D) Does not exist
Answer:
B) All real values except 10

Question 68.
The ratio of two numbers is 3 : 8 and their difference is 115. The largest number is ……………….
A) 115
B) 69
C) 184
D) 240
Answer:
C) 184

Question 69.
The solution of the system of equations 2x + 3y + 5 = 0 and 3x – 2y – 12 = 0 is …………………
A) x = -3, y = 2
B) x = 2, y = -3
C) x = 3, y = -2
D) x = -2, y = 3
Answer:
B) x = 2, y = -3

Question 70.
The solution of the system of equations \(\) = 6 and \(\) + 3 = 0
(where x ≠ 0, y ≠ 0) is ………………….
A) x = 1, y = 2
B) x = -1, y = -2
C) x = 1, y = -2
D) x = -1, y = 2
Answer:
A) x = 1, y = 2

Question 71.
For what value of k, the system of equations kx – y = 2, 6x – 2y – 3 has infinitely many solutions ?
A) k = 2
B) k = 3
C) k = 1
D) Does not exists
Answer:
D) Does not exists

Question 72.
When simple interest is charged a certain principle amounts to Rs. 7400 in 4 years and Rs. 9200 in 7 years. Then the rate of interest is …………………….
A) 6%
B) 18%
C) 14%
D) 12%
Answer:
D) 12%

Question 73.
The age of a woman is four times the age of her daughter. Five years hence, the age of the women will be three times the age of her daughter. The present age of daughter is …………………
A) 40 years
B) 19 years
C) 18 years
D) 20 years
Answer:
B) 19 years

Question 74.
If x, y and y – \(\frac{1}{x}\) are not zero, then \(\frac{x-\frac{1}{y}}{y-\frac{1}{x}}\) equals to ………………….
A) 1
B) \(\frac{\mathrm{x}}{\mathrm{y}}\)
C) \(\frac{\mathrm{y}}{\mathrm{x}}\)
D) \(\frac{x}{y}-\frac{y}{x}\)
Answer:
B) \(\frac{\mathrm{x}}{\mathrm{y}}\)

Question 75.
The solution of \(\sqrt{5 x-1}+\sqrt{x-1}\) = 2 is ………………….
A) x = 5
B) x = \(\frac{2}{3}\)
C) x = 3
D) x = 1
Answer:
D) x = 1

Question 76.
If \(\frac{x}{b}=\frac{y}{a}\), bx + ay = a² + b², then the values of (x, y) are ……………….
A) (a, b)
B) (a, -b)
C) (b, -a)
D) (b, a)
Answer:
D) (b, a)

Question 77.
The coordinates of the points where the lines 3x – y = 5, 6x – y = 10 meet the Y – axis ……………….
A) (0, -5), (0, -10)
B) (-5, 0), (-10, 0)
C) (-5, 0), (0, – 10)
D) (0, -5) (0,10)
Answer:
A) (0, -5), (0, -10)

Question 78.
A toy train crosses 210m and 122m long tunnels in 25 and 17 seconds respectively. The length of the train is…………………
A) 11m
B) 65 m
C) 332 m
D) 88 m
Answer:
B) 65 m

Question 79.
Two numbers are such that their difference, their sum and their product are to one another is 1 : 7 : 24. The product of two numbers is
A) 12
B) 24
C) 48
D) 96
Answer:
B) 24

Question 80.
The solution of the system of equations given by \(\frac{x+y-8}{2}\) = \(\frac{x+2 y-14}{3}\) = \(\frac{3 x+y-12}{11}\)is ……………………
A) x = 3, y = 8
B) x = 4, y = 4
C) x = 2, y = 6
D) x = 6, y = 8
Answer:
C) x = 2, y = 6

Question 81.
The denominator of a rational number is greater than its numerator by 3. If 3 is
subtracted from the numerator and 2 is added to the denominator the new number becomes \(\frac {1}{5}\). Then the original number was ………………….
A) \(\frac {7}{11}\)
B) \(\frac {3}{5}\)
C) \(\frac {5}{8}\)
D) \(\frac {4}{7}\)
Answer:
C) \(\frac {5}{8}\)

Question 82.
For what value of p does the system of equations 2x – py = 0,3x + 4y = 0 has non zero solution ?
A) p = -6
B) p = \(\frac{-8}{3}\)
C) p = \(\frac{-2}{3}\)
D) p = 6
Answer:
B) p = \(\frac{-8}{3}\)

Question 83.
For what value of p will the system of equations 3x + y = 1, (2p – 1)x + (p – 1) y = (2p + 1) has no solution ?
A) p = 2
B) p ≠ 2
C) p = -2
D) p ≠ -2
Answer:
A) p = 2

Question 84.
The income of P and Q are in the ratio 3:2 and expenses are in the ratio 5:3. If both save Rs. 200, what is the income of P?
A) Rs. 700
B) Rs. 1000
C) Rs. 1400
D) Rs. 1200
Answer:
D) Rs. 1200

Question 85.
The sum of the digits of a two digit number is 8. If the digits are reversed, the number is decreased by 54. Find the number.
A) 62
B) 80
C) 71
D) 53
Answer:
C) 71

Question 86.
The ratio between a two-digit number and the sum of digits of that number is 4 : 1. If the digit in the unit place is 3 more than the digit in the tenth place what is that number ?
A) 63
B) 49
C) 86
D) 92
Answer:
A) 63

Question 87.
If (p, p) is the solution of system of equations ax + by + (t – s) = 0 and bx + ay + (s – r) = 0, (a ≠ b) then which of the following must be true ?
A) 2s = r + t
B) r + s + t = 0
C) 2r = s + t
D) 2t = r + s
Answer:
A) 2s = r + t

Question 88.
If the system of equations 4x – 5y = 6 and -12x + ay = b is inconsistent. Which of the following cannot be the value of b?
A) -20
B) -9
C) -7
D) -18
Answer:
D) -18

Question 89.
The present age of father is three times as old as his son. 5 years ago, the father was four times as old as his son. After 5 years fatherer’s age will be ………………….
A) 30 years more than the son’s age
B) 25 years more than the son’s age
C) 32 years more than the son’s age
D) Three times the son’s age
Answer:
A) 30 years more than the son’s age

Question 90.
If x men can do a piece of work in y days, in how many days will z men do the same work ?
A) \(\frac{\mathrm{xy}}{\mathrm{y}}\)
B) \(\frac{x y}{z}\)
C) \(\frac{\mathrm{yz}}{\mathrm{x}}\)
D) XYZ
Answer:
C) \(\frac{\mathrm{yz}}{\mathrm{x}}\)

Question 91.
In ΔABC if ∠A = x°,∠B = 3x°, ∠C = y° and 3y – 5x = 30 then ΔABC is ……………………..
A) a right angled triangle
B) an isosceles triangle
C) an equilateral triangle
D) a right angled isosceles triangle
Answer:
A) a right angled triangle

Question 92.
For the equations 5x – 6y = 2 and 10x = 12y + 7 ………………..
A) There is no solution
B) There exists unique solution
C) There are two solutions
D) There are infinite solutions
Answer:
A) There is no solution

Question 93.
Which of the following system of equations has unique solution ?
A) 3x + y = 2, 6x + 2y = 3
B) 2x – 5y = 3,6x – 15y = 9
C) x – 2y = 3, 3x – 2y = 1
D) 2x – 5y = 7, 6x + 15y = 3
Answer:
C) x – 2y = 3, 3x – 2y = 1

Question 94.
The coordinates of the point where the line 2(x – 3) = y – 8 meet the X – axis ………………
A) (3, 0)
B) (2, 0)
C) (-1, 0)
D)(-2, 0)
Answer:
C) (-1, 0)

Question 95.
For what values of a and b will be equations 2x + 3y = 7, (a – b) x + (a + b)y = (3a + b – 2) represent coincident lines ?
A) a = -5, b = 1
B) a = 5, b = 1
C) a = -5, b = -1
D) a = 5, b = -1
Answer:
B) a = 5, b = 1

Question 96.
The solution for the system of equations 2x – 3y + 4xy = 0 and 6x + 5y – 2xy = 0 is ……………………
A) x = 0, y = 0
B) x = 1, y = -2
C) Both A & B
D) x = -1,y = 2
Answer:
C) Both A & B

Question 97.
If the pair of linear equations x – y = 1, x + ky = 5 has a unique solution x = 2, y = 1 then the value of k is …………………..
A) -2
B) 3
C) 2
D) 4
Answer:
B) 3

Question 98.
If 9^{x + 2} = 240 + 9^x, then the value of “x” is ……………….
A) 0.1
B) 0.2
C) 0.5
D) 0.3
Answer:
C) 0.5

Question 99.
Given b ≠ a, the fractions \(\frac{a x+b}{c x+d}\) and \(\frac{\mathbf{b}}{\mathbf{d}}\) are unequal if …………………..
A) a = c = 1 and x ≠ 0
B) a = b = 0
C) a = c = 0
D) x = 0
Answer:
D) x = 0

Question 100.
The equation \(\sqrt{x+4}-\sqrt{x-3}\) + 1 = 0 has ………………..
A) no root
B) one real root
C) one real root and one imaginary root
D) two imaginary roots
Answer:
A) no root

Question 101.
Which of the following system of equations is consistent ?
A) 3x – y = 1, 6x – 2y = 5
B) 4x + 6y – 7 = 0, 12x + 18y – 21 = 0
C) 4x + 9y = 14, 9x + 8y = 14 .
D) 4x + 12y = 16, 9x + 9y = 14
Answer:
B) 4x + 6y – 7 = 0, 12x + 18y – 21 = 0

Question 102.
A mother said to her son “The sum of our present ages is twice my age 12 years ago and 9 years hence, the sum of our ages will be thrice my age 14 years ago”. What is her son’s present age ? (in years)
A) 18
B) 14
C) 12
D) 10
Answer:
C) 12

Question 103.
Ram has 18 coins in the denominations of Rs.1, Rs. 2 and Rs.5. If their total value is Rs. 54 and the number of Rs. 2 coins are greater than of Rs. 5 coins. Then find the number of Rs. 1 coins with him.
A) 3
B) 1
C) 2
D 5
Answer:
A) 3

Question 104.
Ram, Shyam,Tarun and Varun together had a total amount of Rs. 240 with them. Ram had half of the total amount with the others. Shyam had one-third of the total amount with the others. Tarun had one-fourth of the total mount with the others. Find the amount with Tarun (in Rs.).
A) 78
B) 69
C) 52
D) 92
Answer:
C) 52

Question 105.
A sum of Rs. 400 was distributed among the students of a class. Each boy received Rs. 8 and each girl received Rs. 4. If each girl had received Rs. 10, then each boy would have received Rs. 5. Find the total number of students of the class.
A) 10
B) 20
C) 60
D) 40
Answer:
C) 60

Question 106.
Ramu had 13 notes in the denominations of Rs. 10, Rs. 50 and Rs. 100. The total value of the notes with him was Rs. 830. He had more of Rs. 100 notes than that of Rs. 50 notes with him. Find the number of Rs. 10 notes with him.
A) 9
B) 5
C) 3
D) 7
Answer:
C) 3

Question 107.
Dheeraj has twice as many sisters as he has brothers. If Deepa, Dheeraj’s sister has the same number of brothers as she has sisters, then Deepa has how many brothers ?
A) 3
B) 5
C) 7
D) 9
Answer:
A) 3

Question 108.
The general form of the linear equation in two variables x, y is ……………….
A) ax + by + c = 0, a ≠ 0
B) ax + by + c = 0, | a | + | b | = 0
C) ax + by + c = 0, | a | + | b | ≠ 0
D) ax + by + c = 0, a ≠ 0, b ≠ 0
Answer:
C) ax + by + c = 0, | a | + | b | ≠ 0

Question 109.
If the sum of two numbers is 640 and their difference is 280. Then the numbers are ………………..
A) 140, 500
B) 180, 460
C) 130, 510
D) 150, 490
Answer:
B) 180, 460

Question 110.
The value of ‘m’ in the pair of equations 4x + my + 9 = 0; 3x + 4y + 8 = 0 to have unique solution is ………………….
A) m ≠ 16
B) m ≠ 15
C) m ≠ \(\frac{16}{3}\)
D) m ≠ \(\frac{15}{4}\)
Answer:
C) m ≠ \(\frac{16}{3}\)

Question 111.
A two-digit number is formed by either subtracting 17 from nine times the sum of the digits or by adding 21 to 13 times the difference of the digits. Find the number.
A) 37
B) 73
C) 75
D) 57
Answer:
B) 73

Question 112.
The sum of two numbers is 20 and their product is 64. Then one of the number is ………………..
A) 14
B) 16
C) 42
D) 43
Answer:
B) 16

Question 113.
If the ratio of boys to girls in a class is B arid the ratio of girls to boys in G then B + G is …………………..
A) greater than 1 or equal to 1
B) greater than 1
C) less than 1
D) equal to 1
Answer:
D) equal to 1

Question 114.
The LCM of two numbers is 630 and their HCF is 9. If the sum of the numbers is 153. Their difference is ……………….
A) 81
B) 27
C) 49
D) 92
Answer:
B) 27

Question 115.
Mallesh has some cows and some hens in his shed. The total number of legs is 92 and the total number of heads is 29. Find the number of cows in his shed.
A) 19
B) 17
C) 14
D) 12
Answer:
B) 17

Question 116.
A three digit number abc is 459 more than the sum of its digits. What is the sum of the 2 digit number ab and the 1 digit number a ?
A) 51
B) 61
C) 71
D) 81
Answer:
A) 51

Question 117.
An examination consists of 100 questions. Two marks are awarded for every correct option. If one mark is deducted for every wrong option and half mark is deducted for every question left. Then a person scores 135. Instead, if half mark is deducted for every wrong option and one mark is deducted for every question left, then the person scores 133. Find the number of questions left unattempted by the person.
A) 13
B) 14
C) 19
D) 15
Answer:
B) 14

Question 118.
Total cost of 14 pens and 21 books is Rs. 130 and the total cost of 6 pens and p books is Rs. 90. Which of the following cannot be the value of p ?
A) 4
B) 6
C) 10
D) 9
Answer:
D) 9

Question 119.
The sum of the speeds of a boat in still water and the speed the current is 10 kmph. If the boat takes 40% of the time to travel downstream when compared to that upstream. Then find the difference of the speeds of the boat when travelling upstream and down stream.
A) 4 kmph
B) 6 kmph
C) 8 kmph
D) 5 kmph
Answer:
B) 6 kmph

Question 120.
A told B, “When I was old as you are now, then your age was four years less than half of my present age.” If the sum of the present ages of A and B is 61 years, what is B’s present age ? (in years)
A) 30
B) 25
C) 35
D) 9
Answer:
B) 25

Question 121.
Swaroop can row 16km downstream and 8km upstream in 6 hours. He can row 6km upstream and 24km downstream in 6 hours. Find the speed of Swaroop in still water.
A) 14 kmph
B) 5 kmph
C) 10 kmph
D) 12 kmph
Answer:
B) 5 kmph

Question 122.
If a room is x meters long, y meters broad and z meters high. Then find how many square meters of carpet will be required for the floor and how many square meters of paper for the walls ?
A) xy and 2xy + 2yz
B) xy and 2xz + 2yz
C) xy and 2xy
D) xy and 2xy + 2xz
Answer:
B) xy and 2xz + 2yz

Question 123.
If 15 cups of tea and 17 cups of coffee together cost Rs. 241 and 25 cups of tea and 13 cups of coffee together cost Rs. 279. Then the price of each cup respectively are …………….
A) Rs. 7and Rs. 8
B) Rs. 8 and Rs. 9
C) Rs. 8 and Rs. 10
D) Rs. 6 and Rs. 8
Answer:
A) Rs. 7and Rs. 8

Question 124.
If 1 is added to the denominator of a fraction, the fraction becomes \(\frac {1}{2}\) .If 1 is added to the numerator of the fraction, the fraction becomes 1. Then the fraction is
A) \(\frac {3}{4}\)
B) \(\frac {4}{5}\)
C) \(\frac {1}{2}\)
D) \(\frac {2}{3}\)
Answer:
D) \(\frac {2}{3}\)

Question 125.
If x ≠ 0, \(\) = y² and \(\) = 4y then x equals to ……………..
A) 8
B) 16
C) 128
D) 64
Answer:
C) 128

Question 126.
3 men and 6 boys can finish a piece of work in 3 days, while 2 men and 5 boys can finish it in 4 days. Then time taken by one boy alone to finish the work is ………………
A) 18 days
B) 36 days
C) 24 days
D) 28 days
Answer:
B) 36 days

Question 127.
Divide 62 into two parts such that fourth part of the first and two-fifth part of the second are in the ratio 2 : 3.
A) 24, 38
B) 32, 30
C) 16, 48
D) 40, 28
Answer:
B) 32, 30

Question 128.
The sum of salaries of A and B are Rs. 2100. A spends 80% of his salary and B spends 70%, if their savings are now in the proportion of 4 : 3 what is the salary of A ?
A) Rs. 700
B) Rs. 1000
C) Rs. 1400
D) Rs. 1200
Answer:
C) Rs. 1400

Question 129.
The income of P and Q are in the ratio 3 : 2 and expenses are in the ratio 5:3. If both save Rs. 400 what is the income of P ?
A) Rs. 700
B) Rs. 1000
C) Rs. 1400
D) Rs. 2400
Answer:
D) Rs. 2400

Question 130.
If the units and tens place of a digit number are x and y respectively then the number will be ………………….
A) 10x + y
B) 10y + x
C) xy
D) yx
Answer:
B) 10y + x

Question 131.
Identify parallel lines.

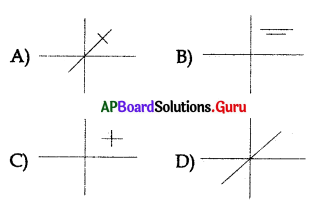
Answer:

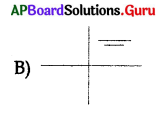
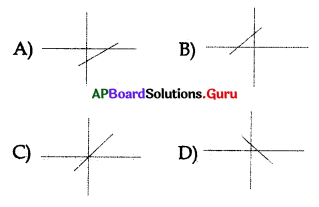
Question 132.
Which of the following line is passing through (0, 0) ?

Answer:

Question 133.
The graph of ax + by + c = 0, may be

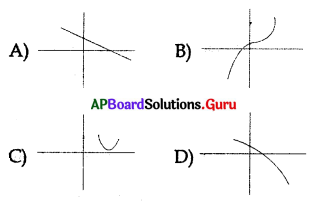
Answer:

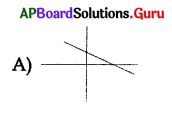
Question 134.
Which of the following are coincident lines?

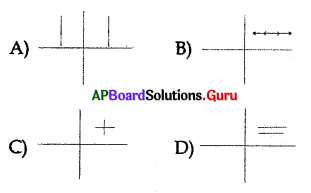
Answer:

Question 135.
The solution of two linear equations lies in Q₁. This can be represented graphically as ………………

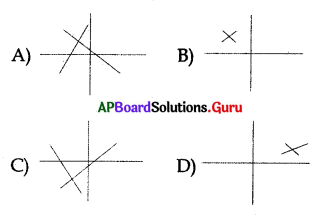
Answer:

Question 136.
Two lines have no solution. The graphical representation can be taken as ………………….

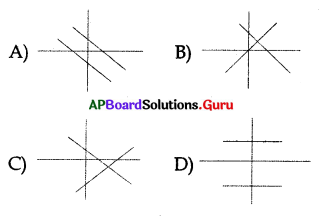
Answer:

Question 137.
Angle between two lines is zero they may be represented as ………………

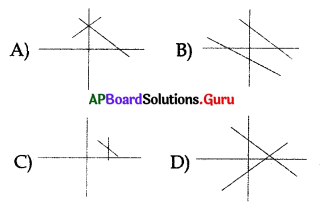
Answer:

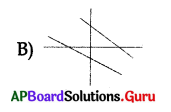
Question 138.
If the pair of equations 2x + 3y + k = 0, 6x+9y + 3 = 0 having infinite solutions, the value of ‘k’ is ……………………
B) 3
C) 0
D) 1
Answer:
D) 1