Category: Class 9

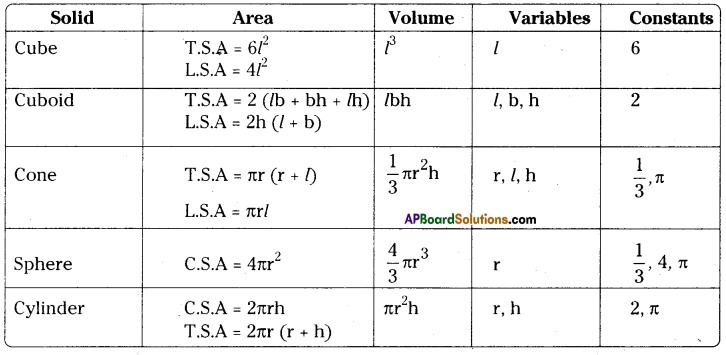
AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles InText Questions

Question
Observe your surroundings carefully and write any three situations of your daily life where you can observe lines and angles. [Page No. 71]
Solution:
The edges of a blackboard; the edges of a ruler/scale and the edges of a table gives the idea of lines and their corners give the idea of angles.

Question
Draw the pictures in your notebook and collect some pictures. [Page No. 71]
Solution:

Think, Discuss and Write

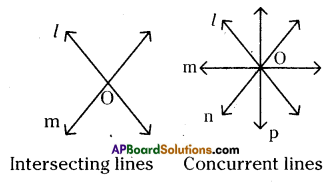
What is the difference between inter-secting lines and concurrent lines ? [Page No. 74]
Solution:
If the number of lines meeting at a point are only two then they are said to be intersecting lines whereas if the lines are three or more than three meeting at a point then they are said to be concurrent lines.

Do These

Question 1.
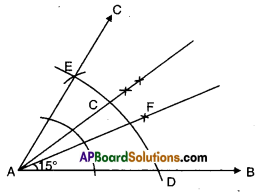
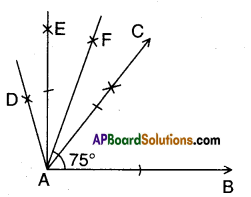
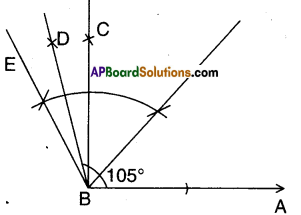
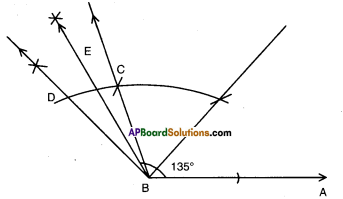
Write the complementary, supplementary and conjugate angles for the following angles, a) 45° b) 75° c) 215° d) 30° e) 60° f) 90° g) 180° [Page No. 76]
Solution:

Question 2.
Which pairs of the following angles become complementary or supplementary. [Page No. 76]

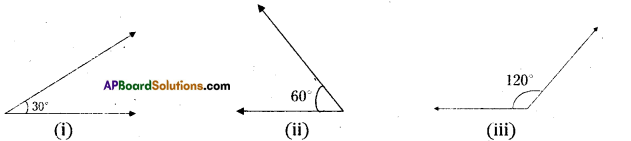
Solution:
The angles formed by the figures (i) and (ii) are complementary.
The angles formed by the figures (ii) and (iii) are supplementary.

Try This

Question 1.
Find the pairs of adjacent and non- adjacent angles in the given figures. [Page No. 77]

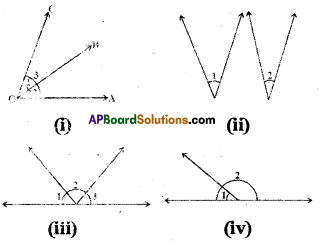
Solution:
In figure (i) ∠1 and ∠2 are pair of adjacent angles.
In figure (ii), no adjacent angles.
In figure (iii) (∠1, ∠2), (∠2, ∠3) are pairs of adjacent angles.
In figure (iv) ∠1 and Z2 are adjacent angles.

ii) List the adjacent angles in the given figure. [Page No. 77]

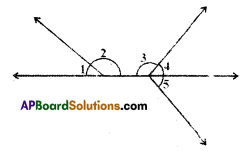
Solution:
In the given figure
(∠1, ∠2), (∠3, ∠4), (∠4,∠5) and (∠3, ∠5) are the pairs of adjacent angles.

Think Discuss and Write

Question
Linear pair of angles are always supplementary. But supplementary angles need not form a linear pair. Why ? [Page No. 77]
Solution:
A pair of supplementary angles need not necessarily a linear pair because they may exists in separate figures.

Activity

Measure the angles in the following figure and complete the table.
[Page No. 78]

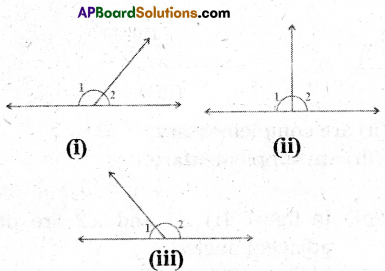
Solution:

Measure the four angles 1,2,3,4 in each of the above figure and complete the table:
[Page No. 79]

Solution:

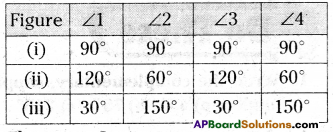
Do This

Question 1.
Classify the given angles as pairs of complementary, linear pair, vertically opposite and adjacent angles. [Page No. 80]

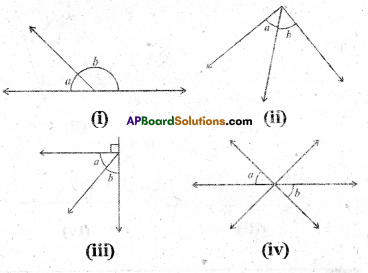
Solution:
The pairs of angles a and b in the fig.(i) are linear pair of angles.
The pairs of angles a and b in the fig.(ii) are adjacent angles.
The pairs of angles a and b in the fig.(iii) are complementary angles*
The pairs of angles a and b in the fig.(iv) are vertically opposite angles.

Question 2.
Find the measure of angle ‘a’ in each figure. Give reasons in each case. [Page No. 81]
i)

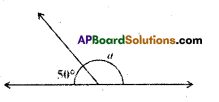
a = 180° – 50° = 130°
(linear pair of angles)

ii)

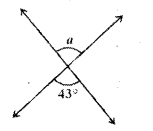
a = 43°
( ∵ vertically opposite angles)

iii)

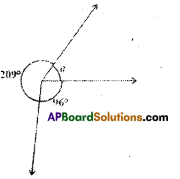
a = 360° – (209° + 96°)
= 360° – 305° = 55°
(∵ complete angle = 360°)

iv)

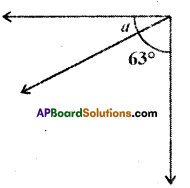
a = 90° – 63° = 27°
(pair of complementary angles )

Do These

Question 1.
Find the measure of each angle indi-cated in each figure where / and m are parallel lines intersected by a transversal n. [Page No. 87]

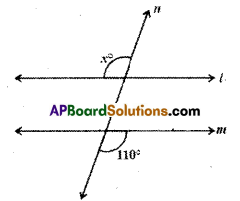
Solution:
x = 110° (alternate exterior angles)

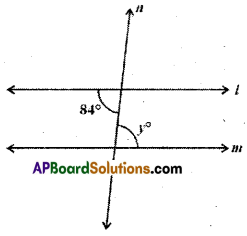
Solution:
y = 84° (alternate interior angles)

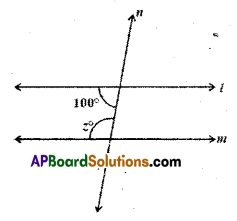
Solution:
z = 180° – 100° = 80° .
(interior angles on the same side of transversal)

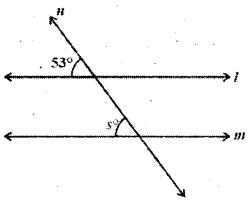
Solution:
s° = 53° (pair of corresponding angles)

Question 2.
Solve for x and give reasons. [Page No. 88]

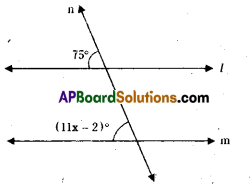
11x + 2 = 75°
11x = 75 – 2 = 73
∴ x = \(\frac{73}{11}\)
(∴ pair of corresponding angles are equal).

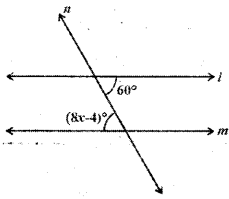
Solution:
8x – 4 = 60°
8x = 60 + 4 = 64
∴ x = \(\frac{64}{8}\) = 8
(∴ alternate interior angles are equal)

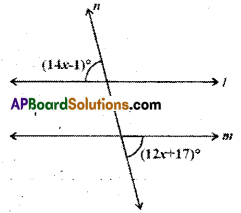
Solution:
(14x- 1)°.= (12x + 17)°
14x – 12x = 17 + 1
2x = 18
x = \(\frac{18}{2}\) = 9
(∴ alternate exterior angles are equal)

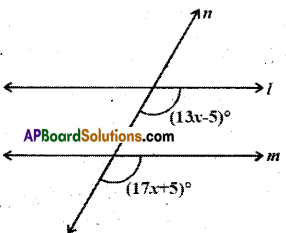
Solution:
13x- 5 = 17x + 5
13x- 17x = 5 + 5
– 4x = 10
x = \(\frac{10}{-4}=\frac{-5}{2}\)
(∴ Pair of, corresponding angles are equal).

Activity

Question 1.
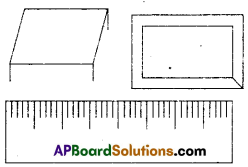
Take a scale and a ‘set sqaure’. Arrange the set sqare on the scale as shown in figure. Along the slant edge of set sqare draw a line with the pencil. Now slide your set square along its horizontal edge and again draw a line. We observe that the lines are parallel. Why are they parallel ? Think and discuss with your friends. [Page No. 88]
Solution:

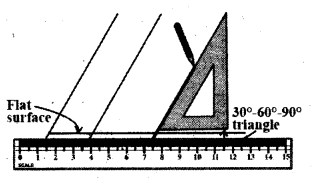
A. Student Activity (For Reference .)
All slant lines are parallel making an angle of 60° with the horizontal line. In this figure horizontal line is transversal to the slant line and corresponding angles are equal.

Do This

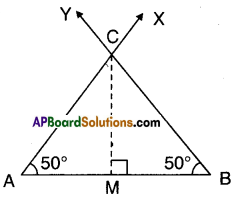
Question
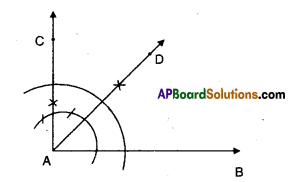
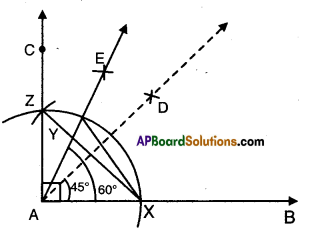
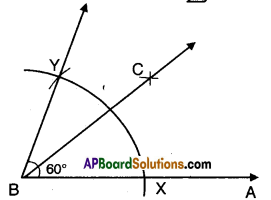
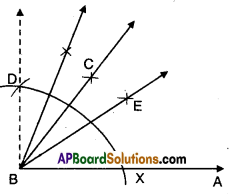
Draw a line \(\overline{\mathbf{A D}}\) and mark points B and C on it. At B and C, construct ∠ABQ and ∠BCS equal to each other as shown. Produce QB and SC on the other side of AD to form two lines PQ and RS.

Draw common perpendiculars EF and GH for the two lines PQ and RS. Measure the lengths of EF and GH. What do you observe ? What can you conclude from that ? Recall that if the perpendicular distance between two lines is the same, then they are parallel lines. [Page No. 89]


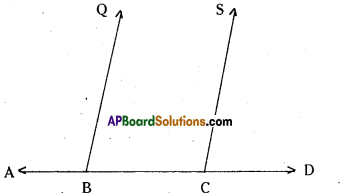
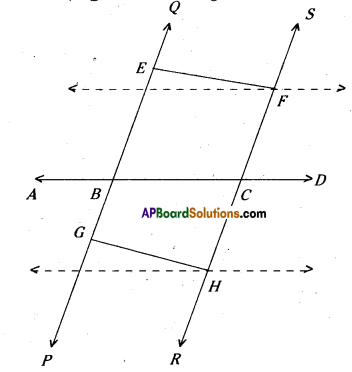
Solution:
As ∠ABQ =∠BCS and they lie on the same line AD we can say that BQ // CS. Now EF and GH are the perpendicular distances between two parallel lines PQ and R, we say EF = GH.

Try This

Question i)
Find the measure of the question marked angle in the given figure. [Page No. 90]

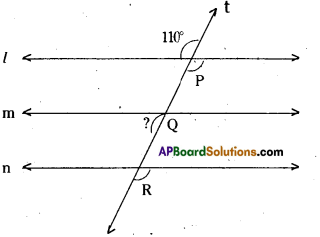
Solution:
? = 70°
[ ∵ from the figure, these two angles are exterior angles on the same side of the transversal]

ii) Find the angles which are equal to ∠P.
Solution:
∠P = ∠Q = ∠R = 110°
(corresponding angles)

Activity

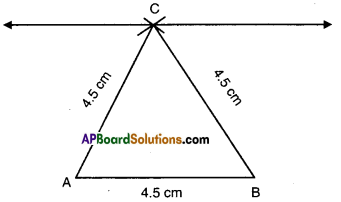
Question
Draw and cut out a large triangle as shown in the figure.
Number the angles and tear them off.
Place the three angles adjacent to each other to form one angle as shown below. [Page No. 97]

1. Identify angle formed by the three adjacent angles ? What is its mea-sure ?
2. Write about the sum of the measures of the angles of a triangle. Now let us prove this statement
using the axioms; and theorems related to parallel lines.
Solution:
Student Activity.

Think, Discuss and Write

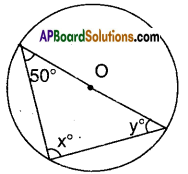
Question
If the sides of a triangle are produced in order, what will be the sum of exterion angles formed ? [Page No. 99]
Solution:
Let ΔABC and the sides of the triangle is formed by exterior angles.

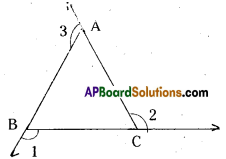
∠3 = ∠B + ∠C
∠1 + ∠2 + Z∠3 = 2[∠A + ∠B + ∠C]
= 2 x 180° = 360°
∴ Sum of the exterior angles are 360°.

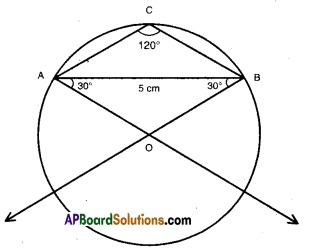
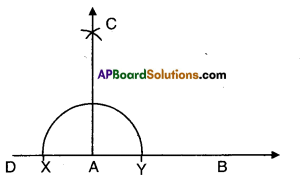
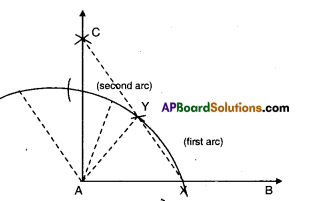AP Board 9th Class Maths Solutions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 3 The Elements of Geometry InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 3rd Lesson The Elements of Geometry InText Questions

Try This

Can you give any two axioms from your daily life. [Page No. 63]
Solution:
Example -1 : If we flip coin then there are only two chances that is head or tail.
Example – 2 : Things which are equal to the same thing are also equal to one another.
Example – 3 : The whole is greater than the part.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation InText Questions

Think, Discuss and Write

Question
Which of the following expressions are polynomials ? Which are not ? Give reasons. [Page No. 28]
Solution:
i) 4x² + 5x – 2 is a polynomial.
ii) y² – 8 is a polynomial.
iii) 5 is a constant polynomial.
iv) \(2 x^{2}+\frac{3}{x}-5\) is not a polynomial as x is in denominator.
v) √3x² + 5y is a polynomial.
vi) \(\frac{1}{x+1}\) is not a polynomial as the variable x is in denominator.
vii) √x is not a polynomial as its exponent is not an integer.
viii) 3xyz is a polynomial.

Do These

Question
Write two polynomials with variable ‘x’. [Page No. 29]
Solution:
5x² + 2x – 8 and 3x² – 2x + 6.

Question
Write three polynomials with variable ‘y’.
Solution:
y³ – y² + y ; 2y² + 7y – 9 + 3y³; y⁴ – y + 6 + 2y².

Question
Is the polynomial 2x² + 3xy + 5y² in one variable ?
Solution:
No. It is in two variables x and y.

Question
Write the formulae of area and volume of different solid shapes. Find out the variables and constants in them. [Page No. 29]
Solution:

Question 1.
Write the degree of each of the following polynomials. [Page No. 30]
Solution:
i) 7x³ + 5x² + 2x – 6 – degree 3
ii) 7 – x + 3x² – degree 2
iii) 5p – √3 – degree 1
iv) 2 – degree 0
v) – 5 xy² – degree 3

Question 2.
Write the co-efficient of x² in each of the following. [Page No. 30]
Solution:
i) 15 – 3x + 2x² : co-efficient of x² is 2
ii) 1 -x² : co-efficient of x² is -1
iii) πx² – 3x + 5 : co-efficient of x² is π
iv) √2x² + 5x – 1 : co-efficient of x² is √2

Think, Discuss and Write

Question
How many terms a cubic (degree 3) polynomial with one variable can have? Give examples. [Page No. 31]
Solution:
A cubic polynomial can have atmost 4 terms.
E.g.: 5x³ + 3x² – 8x + 4; x³ – 8

Try These

Question 1.
Write a polynomial with 2 terms in variable x. [Page No. 31]
Solution:
2x + 3x²

Question 2.
How can you write a polynomial with 15 terms in variable ‘x’. [Page No. 31]
Solution:
a₁₄p¹⁴ + a₁₃p¹³ + a₁₂p¹²+ …………….+ a₁p + a₀

Do This

Question
Find the value of each of the follow ing polynomials for the indicated value of variables. [Page No. 33]
(i) p(x) = 4x² – 3x + 7 at x = 1.
Solution:
The value of p(x) at x = 1 is
4(1)² – 3(1) + 7 = 8

ii) q(y) = 2y³ – 4y + √11 at y = 1.
Solution:
The value of q(y) at y = 1 is
2(1)³ – 4(1) + √11 = -2 + √11

iii) r(t) = 4t⁴ + 3t³ – t² + 6 at t = p, t ∈ R.
Solution:
The value of r(t) at t = p is
4p⁴ + 3p³ – p² + 6

iv) s(z) = z³ – 1 at z – 1.
Solution:
The value of s(z) at z = 1 is 1³ – 1 = 0

v) p(x) = 3x² + 5x – 7 at x = 1.
Solution:
The value of p(x) at x = 1 is
3(1)² + 5(1) — 7 = 1.

vi) q(z) = 5z³ – 4z + √2 at 7. = 2.
Solution:
The value of q(z) at z = 2 is
5(2)³ – 4(2) + √2 = 40 – 8 + √2
= 32 + √2

Try These

Question
Find zeroes of the following polyno¬mials. [Page No. 34]

1. 2x-3
Solution:
2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)
∴ x = \(\frac{3}{2}\) is the zero of 2x – 3.

2. x² – 5x + 6
Solution:
x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x (x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x – 2 = 0 or x – 3 = 0
⇒ x = 2 or x = 3
∴ x = 2 or 3 are the zeroes of x² – 5x + 6.

3. x + 5
Solution:
x + 5 = 0
x = – 5
∴ x = – 5

Do This

Fill in the bianks : [Page No. 35]

Solution:

Think, and Discuss

Question 1.
x² + 1 has no zeroes. Why ? [Page No. 36]
Solution:
x² + 1 = 0 ⇒ x² = -1
No real number exists such that whose root is – 1.
∴ x² + 1 has no zeroes.

Question 2.
Can you tell the number of zeroes of a polynomial of degree ‘n’ will have? [Page No. 36]
Solution:
A polynomial of degree n will have n- zeroes.

Do These

Question 1.
Divide 3y³ + 2y² + y by ‘y’ and write division fact. [Page No. 38]
Solution:
(3y³ + 2y² + y) ÷ y = \(\frac{3 y^{3}}{y}+\frac{2 y^{2}}{y}+\frac{y}{y}\)
= 3y² + 2y + 1
Division fact = (3y² + 2y + 1) y
= 3y³ + 2y² + y

Question 2.
Divide 4p² + 2p + 2 by ‘2p’ and write division fact.
Solution:
4p² + 2p ÷ 2 = \(\frac{4 p^{2}}{2 p}+\frac{2 p}{2 p}+\frac{2}{2 p}\)
= 2p + 1 + \(\frac{1}{\mathrm{P}}\)
Division fact:
(2p + 1 + \(\frac{1}{\mathrm{P}}\)).2p = 4p² + 2p + 2

Try These

Show that (x – 1) is a factor of xⁿ – 1. [Page No. 45]
Solution:
Let p(x) = xⁿ – 1
Then p(1) = 1ⁿ – 1 = 1 – 1 = 0
As p(1) = 0, (x – 1) is a factor of p(x).

Do These

Question
Factorise the following. [Page No. 46]

1. 6x² + 19x + 15
Solution:
6x² + 19x + 15 = 6x² + 10x + 9x + 15
= 2x (3x + 5) + 3 (3x + 5)
= (3x + 5) (2x + 3)

2. 10m² – 31m – 132
Solution:
10m² – 31m – 132
= 10m² – 55m + 24m – 132
= 5m (2m- 11) + 12 (2m- 11)
= (2m – 11) (5m + 12)

3. 12x² + 11x + 2
Solution:
12x² + 11x + 2
= 12x² + 8x + 3x + 2
= 4x (3x + 2) + 1 (3x + 2)
= (3x + 2) (4x + 1)

Try This

Question
Try to draw the geometrical figures for other identities. [Page No. 49]
i) (x + y)² ≡ x² + 2xy + y²

Step – 1 : Area of fig. I = x x = x²
Step – 2 : Area of fig. II = x y = xy
Step – 3 : Area of fig. III = x y = xy
Step – 4 : Area of fig. IV = y y = y²

Area of big square = sum of the areas of figures I, II, III and IV
∴ (x + y) (x + y) = x² + xy + xy + y²
(x + y)² = x² + 2xy + y²

ii) (x + y) (x – y) ≡ x² – y²

Step -1: Area of fig! I = x (x – y) = x² – xy
Step – 2: Area of fig. II = (x – y) y = xy – y²
Area of big rectangle = sum of areas of figures I & II
(x + y) (x – y) = x² – xy + xy – y²
= x² – y²
∴ (x + y) (x-y) = x2-y2

iii) (x + a) (x + b) ≡ x² + (a + b) x + ab

Step – 1 : Area of fig. I = x²
Step – 2 : Area of fig. II = ax
Step – 3 : Area of fig. Ill = bx
Step – 4 : Area of fig. IV = ab
∴ Area of big rectangle = Sum of areas of four small figures.
∴ (x + a) (x + b) = x² + ax + bx + ab
(x + a) (x + b) = x² + (a + b) x + ab

Do These

Question
Find the following product using appropriate identities. [Page No. 49]
i) (x + 5) (x + 5)
Solution:
(x + 5) (X + 5) = (x + 5)²
= x² + 2(x) (5) + 5²
= x² + 10x + 25

ii) (p – 3) (p + 3)
Solution:
(p – 3) (p + 3)
= p² – 3²
= p² – 9

iii) (y – 1) (y – 1)
Solution:
(y – 1) (y – 1)
= (y – 1)²
= y² – 2y + 1

iv) (t + 2) (t + 4)
Solution:
(t + 2) (t + 4)
= t² + t(2 + 4) + 2 x 4
= t² + 6t + 8

v) 102 x 98
Solution:
102 x 98 = (100 + 2) (100 -2)
= 100² – 2²
= 10000 – 4
= 9996

Do These

Question
Factorise the following using appro-priate identities. [Page No. 50]
i) 49a² + 70ab + 25b²
Solution:
49a² + 70ab + 25b²
= (7a)² + 2 (7a) (5b) + (5b)²
= (7a + 5b)²
= (7a + 5b)(7a + 5b)

ii) \(\frac{9}{16} x^{2}-\frac{y^{2}}{9}\)
Solution:

iii) t² – 2t + 1
= (t)² – 2(t) (1) + (1)²
= (t – 1)² = (t – 1) (t – 1)

iv) x² + 3x + 2
Solution:
x² + 3x + 2 = x2 + (2 + 1) x + (2 x 1)
(x + 2) (x + 1)

Do These

Question i)
Write (p + 2q + r)² in expanded form. [Page No. 52]
Solution:
(p + 2q + r)² = (p)² + (2q)² + (r)²
+ 2 (P) (2q) + 2 (2q) (r) + 2(r) (p)
= p² + 4q² + r² + 4pq + 4qr + 2rp

Question ii)
Expand (4x – 2y – 3z)² using identity. [Page No. 52]
Solution:
(4x – 2y – 3z)² = (4x)² + (- 2y)² + (- 3z)² + 2 (4x) (- 2y) + 2 (- 2y) (- 3z) + 2 (- 3z) (4x)
= 16x² + 4y² + 9z² – 16xy + 12yz – 24zx.

Question iii)
Factorise 4a² + b² + c² – 4ab + 2bc – 4ca
using identity. [Page No. 52]
Solution:
4a² + b² + c² – 4ab + 2bc – 4ca
= (2a)² + (- b)² + (- c)² + 2(2a) (- b) + 2 (- b) (- c) + 2(- c) (2a)
= (2a – b – c)² = (2a – b – c) (2a – b – c)

Try These

Question
How can you find (x – y)³ without actual multiplication ? Verify with actual multiplication. [Page No. 52]
Solution:
(x – y)³ = x³ – 3x²y + 3xy² – 3y³ from identity.
By actual multiplication
(x – y)³ = (x – y)² (x – y)
= (x² – 2xy + y²) (x – y)
= x³ – 2x²y + xy² – x²y + 2xy² – y³
= x³ – 3x² y + 3xy² – y³
Both are equal.

Do These

Question 1.
Expand (x + 1)³ using an identity. [Page No. 54]
Solution:
(x + 1)³ = (x)³ + (1)³ + 3 (x) (1) (x + 1)
= x³ + 1 + 3x (x + 1)
= x³ + 1 + 3x² + 3x = x³ + 3x² + 3x + 1

Question 2.
Compute (3m – 2n)³. [Page No. 54]
Solution:
(3m-2n)³
=(3m)³ – 3 (3m)² (2n) + 3 (3m) (2n)² – (2n)³
= 27m³ – 54m²n + 36mn² – 8n³

Question 3.
Factorise a³ – 3a²b + 3ab² – b³. [Page No. 54]
Solution:
a³ – 3a²b + 3ab² – b³
= (a)³ – 3 (a)² (b) + 3 (a) (b)² – (b)³
= (a – b)³
= (a – b) (a – b) (a – b)

Do These

Question 1.
Find the product (a – b – c) (a² + b² + c² – ab + be – ca) without actual multi-plication. [Page No. 55]
Solution:
The problem is incorrect.

Question 2.
Factorise 27a³ + b³ + 8c³ – 18abc using identity. [Page No. 55]
Solution:
27a³ + b³ + 8c³ – 18abc
= (3a)³ + (b)³ + (2c)³ – 3(3a) (b) (2c)
= (3a + b + 2c) (9a² + b² + 4c² – 3ab – 2be – 6ca)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers InText Questions

Do This

Question 1.
Represent \(\frac{-3}{4}\) on a number line. (Page No.3)
Solution:

Step – 1: Divide each unit into four equal parts to the right and left side of zero on the number line.
Step – 2 : Take 3 parts after zero on its left side.
Step -3 : It represents \(\frac{-3}{4}\)

Question 2.
Write 0, 7, 10, -4 in p/q form (Page No.2)
Solution:

Question 3.
Guess my number : Your friend chooses an integer between 0 and 100. You have to find out that number by asking questions, but your friend can only answer ‘Yes’ or ‘No’. What strategy would you use ? (Page No.3)
Solution:
Let my friend choosen 73; then my questions may be like this.

Q : Does it lie in the first 50 numbers ?
A: No .

Q : Does it lie between 50 and 60 ?
A: No

Q : Does it lie between 60 and 70 ?
A: No

Q : Does it lie between 70 and 80 ?
A: Yes
[then my guess would be “it is a number from 70 to 80]

Q : Is it an even number ?
A: No
[my guess : it should be one of the numbers 71, 73, 75, 77 and 79]

Q : Is it a prime number ?
A: Yes
[my guess : it may be 71, 73 or 79]

Q : Is it less than 75 ?
A: Yes
[my guess : it may be either 71 or 73]

Q : Is it less than 72 ?
A: No

Then the number is 73.
Therefore the strategy is
→ Use number properties such as even, odd, composite or prime to determine the number.

Do This

Question (i)
Find five rational numbers between 2 and 3 by mean method. (Page No.4)
Solution:
We know that \(\frac{a+b}{2}\) is a rational
between any two numbers a and b.
Let a = 2 and b = 3

Question (ii)
Find 10 rational numbers between \(\frac{-3}{11}\) and \(\frac{8}{11}\) (Page No.4)
Solution:
\(\frac{-3}{11}<\left[\frac{-2}{11}, \frac{-1}{11}, \frac{0}{11}, \frac{1}{11}, \frac{2}{11}, \frac{3}{11}, \frac{4}{11}, \frac{5}{11}, \frac{6}{11}, \frac{7}{11}\right]<\frac{8}{11}\)

Do This

Question
Find the decimal form of
(i) \(\frac{1}{17}\) (Page No.5)
Solution:

\(\frac{1}{19}\) = 0.052631

(ii) \(\frac{1}{19}\)(Page No.5)
Solution:

Try These

Question 1.
Find the decimal values of the following. (Page No.6)
Solution:
i) \(\frac{1}{2}\) = 0.5
ii) \(\frac{1}{2^{2}}=\frac{1}{4}\) = 0.25
iii) \(\frac{1}{5}\) = 0.2
iv) \(\frac{1}{5 \times 2}=\frac{1}{10}\) = 0.1
v) \(\frac{3}{10}\) = 0.3
vi) \(\frac{27}{25}\)

vii) \(\frac{1}{3}\)
Solution:

viii) \(\frac{7}{6}\)
Solution:

ix) \(\frac{5}{12}\)
Solution:

x) \(\frac{1}{7}\)
Solution:

Think, Discuss and Write

Question 1.
Kruthi said √2 can be written as \(\frac{\sqrt{2}}{1}\) which is in form. So √2 is a rational number. Do you agree with her argument ? (Page No.10)
Solution:
No.
Writing √2 = \(\frac{\sqrt{2}}{1}\) is not in the \(\frac { p }{ q }\) form.
Since p and q are integers and √2 is not an integer.

Try These

Question 1.
Find the value of √3 upto six decimals.(Page No.10)
Solution:

Step 1 :
Write 3 as 3.00 00 00 00 00 00 00
Step – 2 :
Group the zeros in pairs (i.e.) make periods.
Step – 3 :
Find the square root using long division method.
∴ √3 = 1.732050

Try These

Question 1.
Locate √5 and -√5 on the number line [Hint 5 = 2² + 1²](Page No.12)
Solution:
Step – 1 :
At zero draw a rectangle of length 2 units and breadth 1 unit.

Step – 2 :

Step – 3 :
Using compass draw an arc of radius OB with centre ‘O’ which cuts the num-ber line at D and D¹.

Step – 4 :
D represents √5 and D¹ represents – √5 on the number line.

Activity

Question
Constructing the ‘Square root spiral’. (Page No. 15)
Solution:
Take a large sheet of paper and construct the ‘Square root spiral’ in the following manner.
Step – 1 : Start with point ‘O’ and draw a line segment \(\overline{\mathrm{OP}}\) of 1 unit length.
Step – 2 : Draw a line segment \(\overline{\mathrm{PQ}}\) perpendicular to \(\overline{\mathrm{OP}}\) of unit length (where OP = PQ = 1) (see Fig.)
Step – 3 : Join 0, Q. (OQ = √2 )
Step – 4 : Draw a line segment OR of unit length perpendicular to \(\overline{\mathrm{OQ}}\)
Step – 5 : Join O, R. (OR = √3 )
Step – 6 : Draw a line segment RS of unit length perpendicular to \(\overline{\mathrm{OR}}\).
Step – 7 : Continue in this manner for some more number of steps, you will create a
beautiful spiral made of line segment \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{ST}}, \overline{\mathrm{TU}}\) …………etc. Note that the line segments \(\overline{\mathrm{OQ}}, \overline{\mathrm{OR}}, \overrightarrow{\mathrm{OS}}, \overline{\mathrm{OT}}, \overline{\mathrm{OU}}\) …… etc., denote the lengths √2,√3, √4, √5, √6 respectively.

Do This

Question 1.
Find rationalising factors of the denominators of (Page No. 20)
i) \(\frac{1}{2 \sqrt{3}}\)
Solution:
\(\frac{1}{2 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{2 \times 3}=\frac{\sqrt{3}}{6}\)
∴ The R.F is √3

ii) \(\frac{1}{\sqrt{5}}\)
Solution:
\(\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{3 \sqrt{5}}{5}\)
∴ The R.F is √5

iii) \(\frac{1}{\sqrt{8}}\)
Solution:

Do This;

Question
Simplify : (Page No. 23)

i) (16) ^1/2
Solution:
(16)^1/2 = (4 x 4)^1/2 = (42)^1/2 = 4^2/2 = 4

ii) (128)^1/7
Solution:
(128)^1/7 =(2 X 2 X 2 X 2 X 2 X 2 X 2)^1/7 = (2⁷)^1/7 = 2

iii) (343)^1/5
Solution:
(343)^1/5= (3 x 3 x 3 x 3 x 3)^1/5 = (3⁵)^1/5= 3

Question 1.
Write the following surds in exponen-tial form (Page No. 24)
i) √2
Solution:
√2 = 2^1/2

ii) 3√9
Solution:
\(\sqrt[3]{9}=\sqrt[3]{3 \times 3}=\sqrt[3]{3^{2}}=3^{\frac{2}{3}}\)

iii) \(\sqrt[5]{20}\)
Solution:
\(\begin{aligned}
\sqrt[5]{20}=\sqrt[5]{2 \times 2 \times 5} &=\sqrt[5]{2^{2} \times 5} \\
&=2^{\frac{2}{5}} \times 5^{\frac{1}{5}}
\end{aligned}\)

iv) 17√19
Solution:
\(\sqrt[17]{19}=19^{\frac{1}{17}}\)

Question 2.
Write the surds in radical form. (Page No. 24)
i) 5^1/7 = \(\sqrt[7]{5}\)
ii) 17^1/6 = \(\sqrt[6]{17}\)
iii) 5^2/5 = \(\sqrt[5]{5^{2}}=\sqrt[5]{5 \times 5}=\sqrt[5]{25}\)
iv) 142^1/2 = \(\sqrt{142}\)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.4

Question 1.
State which of the following are mathematical statements and which are not ? Give reason.
i) She has blue eyes.
Solution:
This is not a mathematical statement. no mathematics is involved in it.

ii) x + 7 = 18
Solution:
This is not a statement, as its truthness cant be determined.

iii) Today is not Sunday.
Solution:
This is not a statement. This is an am biguous open sentence.

iv) For each counting number x, x + 0 = x.
Solution:
This is a mathematical statement.

v) What tune is it?
Solution:
This is not a riathematical statement.

Question 2.
Find counter examples to disprove the following statements.
i) Every rectangle is a square.
Solution:

A rectangle and square are equiangular i.e., all the four angles are right angles. This doesn’t mean that they have equal sides.

ii) For any integers x and y,
\(\sqrt{x^{2}+y^{2}}\) = x + y
Solution:
Let x = 3; y = 8
\(\sqrt{x^{2}+y^{2}}=\sqrt{3^{2}+8^{2}}\)
= \(\sqrt{9+64}=\sqrt{73}\)

x + y = 3 + 8 = 11
Here, √73 ≠ 11
i.e., \(\sqrt{x^{2}+y^{2}}\) ≠ x + y

iii) If n is a whole number then 2n² +11 is a prime.
Solution:
If n = 11 then 2n²+ 11 = 2 (11)² + 11
= 11 (2 × 11 + 1) = 11 × (22 + 1)
= 11 × 23 is not a prime.

iv) Two triangles are congruent if all their corresponding angles are equal.
Solution:

If the corresponding angles are equal then the triangles are only similar.

v) A quadrilateral with all sides are equal is a square.
Solution:
A rhombus is not a square, but all its sides are equal.

Question 3.
Prove that the sum of two odd numbers is even.
Solution:

Question 4.
Prove that the product of two even numbers is an even number.
Solution:

Question 5.
Prove that if x is odd, then x² is also odd.
Solution:
Let x be an odd number.
Then x = 2m + 1
(general form of ah odd number) Squaring on both sides,
x² = (2m + 1)²
= 4m² + 4m +1
= 2 (2m² + 2m) + 1
= 2K + 1 where K = 2m²+ 2
Hence x² is also odd.

Question 6.
Examine why they work ?
Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.
Solution:
Choose a number = x say
Double it = 2x
Add nine = 2x + 9
Add your original number
= 2x + 9 + x = 3x + 9
Divide by 3 = (3x + 9) ÷ 3
= \(\frac{3 x}{3}+\frac{9}{3}\) = x + 3
Add 4 ⇒ x + 3 + 4 = x + 7
Subtract your original number =
x + 7 – x = 7
Your result is 7 – True.

ii) Write down any three digit number (for example, 425). Make a six digit number by repeating these digits in the same order 425425. Your new number is divisible by 7, 11 and 13.
Solution:
Let a three digit number be xyz.
Repeat the digit = xyzxyz
= xyz × (1001)
= xyz × (7 × 11 × 13)
Hence the given conjecture is true.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.3

Question 1.
Take any three consecutive odd numbers and find their product, for example 1 × 3 × 5 = 15;
3 × 5 × 7 = 105: 5 × 7 × 9 = ……………
ii) Take any three consecutive even numbers and add them, say,
2 + 4 + 6 = 12; 4 + 6 + 8 = 18:
6 + 8 + 10 = 24; 8 + 10 + 12 = 30 ….
so on. Is there any pattern you can guess in these sums ? What can von conjecture about them ?
Solution:
i) 1 × 3 × 5 = 15
3 × 5× 7 = 105
5 × 7 × 9 = 315
7 × 9 × 11 = 693

1. The product of any three consecutive odd numbers is odd.
2. The product of any three consecutive odd numbers is divisible by ’3′.
3. 2 + 4 + 6 = 12; 4 + 6 + 8= 18;
   6 + 8 + 10 = 24; 8 + 10 + 12 = 30
4. The sum of any three consecutive even numbers is even.
5. The sum of any three consecutive even numbers is divisible by 6
6. The sum of any three consecutive even numbers is a multiple of 6.

Question 2.
Go back to Pascal’s triangle.
Line-1: 1=11°
Line-2: 11 = 11¹
Line-3 : 121 = 11²
Make a conjecture about line – 4 and line – 5.

Does your conjecture hold ? Does your conjecture hold for line – 6 too ?
Solution:
Line-4 : 1331 = 11³
Line-5 : 14641 = 11⁴
Line – 6 : 11⁵
∴ Line – n = 11^n-1
Yes the conjecture holds good for line – 6 too.

Question 3.
Look at the following pattern.
i) 28 = 2² × 7¹;
Total number of factors
(2+ 1)(1 + 1) = 3 × 2 = 6
28 is divisible by 6 factors i.e.,
1, 2, 4, 7, 14, 28.
ii) 30 = 2¹ × 3¹ × 5¹, Total number of .
factors (1 + 1) (1 + 1) (1 + 1) = 2 × 2 × 2 = 8
30 Is divisible by 8 factors i.e., 1, 2, 3, 5, 6, 10, 15 and 30
Find the pattern.
[Hint : Product of every prime base exponent +1)
Solution:
24 = 2³ × 3¹
24 has (3+1) (1 + 1) = 4 × 2 = 8 factors
[1, 2, 3, 4, 6, 8, 12 and 24]
36 = 2² × 3²
Number of factors = (2 + 1) (2 + 1)
3 × 3 = 9 [ 1, 2, 3. 4, 6, 9, 12, 18 and 36]
If N = a^p. b^q . c^r…….. where N is a natural number.
a. b, c … are primes and p, q, r ……. are positive integers then, the number of factors of N =(p- 1)(q+ 1)(r + 1)

Question 4.
Look at the following pattern :
1² = 1
11² = 121
111² = 12321;
1111² = 1234321
11111² = 123454321
Make a conjecture about each of the following
111111² =
1111111² =
Check if your conjecture is true.
Solution:
111111² = 12345654321
1111111² = 1234567654321
(111………. n-times)² = (123 … (n- 1) n (n – 1) (n – 2) 1)
The conjecture is true.

Question 5.
List five axioms (postulates) used in text book.
Solution:

1. Things which are equal to the same things are equal to one another.
2. If equals are added to equals, the sums are equal.
3. If equals are subtracted from equals, the differences are equal.
4. When a pair of parallel lines are in-tersected by a transversal, the pairs of corresponding angles are equal.
5. There passes infinitely many lines through a given point.

Question 6.
In a polynomial p(x) = x² + x + 41 put different values of x and find p(x). Can you conclude after putting different values of x that p(x) is prime for all. Is ‘x’ an element of N ? Put x = 41 in p(x). Now what do you find ?
Solution:
p(x) = x² + x + 41
p(0) = 0² + 0 + 41 = 41 – is a prime
p(1) = 1² + 1 + 41 = 43 – is a prime
p(2) = 2² + 2 + 41 = 47 – is a prime
p(3) = 3² + 3 + 41 = 53 – is a prime
p(41) = 41² + 41 + 41
= 41(41 + 1 + 1)
= 41 x 43 is not a prime.
∴ p(x) = x²+ x + 41 is not a prime for all x.
∴ The conjecture “p(x) = x² + x + 41 is a prime” is false.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.2

Question 1.
Use deductive reasoning to answer the following.

i) Human beings are mortal. Jeevan is a human being. Based on these two statements, what can’ you conclude about Jeevan?
Solution:
From the above statements we can deduce that Jeevan is mortal as it is given that all humans are mortal and Jeevan is a human.

ii) All Telugu people are Indians. X is an Indian. Can you conclude that X belongs to Telugu people?
Solution:
No. X may belong to any other language like Tamil, Kannada, Malayali…. etc.

iii) Martians have red tongues. Gulag is a Martian. Based on these two statements, what can you conclude about Gulag?
Solution:
Gulag had red, tongue.

iv) What is the fallacy in the Raju’s reasoning in the cartoon below

Solution:
All smarts need not be a President. There could be some other persons who are smart too.

Question 2.
Once again you are given four cards. Each card has a number printed on one side and a letter on the other side. Which are the only two cards you need to turn .over to check whether the following rule holds ?
“If a card has a consonant on one side, then it has an odd number on the other side”.

Solution:
You need to turn over B and 8 only. If B has an even number then the rule has broken. Similarly if 8 has a consonant on the other side then also the rule has been broken.

Question 3.
Think of this puzzle. What do you need to find a chosen number from this square ? Four of the clues below are true but do nothing to help in finding the number. Four of the clues are necessary for finding it.
Here are eight clues to use:
a) The number is greater than 9.
b) The number is not a multiple of 10.
c) The number is a multiple of 7.
d) The number is odd.
e) The number is not a multiple of 11.
f) The number is less than 200.
g) Its ones digit is larger than its tens digit.
h) Its tens digit is odd.
What is the number ?

Solution:

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.1

Question 1.
State whether the following sentences are always true, always false or ambiguous. Justify your answer.
i) There are 27 days in a month.
Solution:
Always false. Generally 30 days or 31 days make a month except February.

ii) Makarasankranthi fells on a Friday.
Solution:
Ambiguous. Makarasankranthi may fall on any day of the week.

iii) The temperature in Hyderabad is 2°C.
Solution:
Ambiguous. Sometimes the temperature may go down to 2°C in winter.

iv) The earth is the only planet where life exist.
Solution:
We can’t say always true. To the known fact, so far we can say this.

v) Dogs can fly.
Solution:
Always false,’as dogs can never fly.

vi) February has only 28 days.
Solution:
Ambiguous. A leap year has 29 days for February.

Question 2.
State whether the following statements are true or false. Give reasons for your answers.

i) The sum of the interior angles of a quadrilateral is 350°.
Solution:
False. Sum of the interior angles of a quadrilateral is 360°.

ii) For any real number x, x² > 0
Solution:
True. This is true for all real numbers,

iii) A rhombus is a parallelogram.
Solution:
True. In a rhombus, both pairs of opposite sides are parallel and hence every rhombus is a parallelogram.

iv) The spm of two even numbers is even.
Solution:
True. This is true for any two even numbers.

v) Square numbers can be written as the sum of two odd numbers.
Solution:
Ambiguous. Since square of an odd number can’t be written as sum of two odd numbers.

Question 3.
Restate the following statements with appropriate conditions, so that they become true statements.

i) All numbers can be represented in prime factorization.
Solution:
Any natural number greater than 1 can be represented in prime factorization.

ii) Two times a real number is always even.
Solution:
Two times a natural number is always even.

iii) For any x, 3x + 1 > 4.
Solution:
For any x > 1; 3x + 1 > 4.

iv) For any x, x³ ≥ 0.
Solution:
For any x > 0; x³ ≥ 0.

v) In every triangle, a median is also an angle bisector.
Solution:
In an equilateral triangle, a median is also an angle bisector.

Question 4.
Disprove, by finding a suitable counter example, the statement
x² > y² for all x > y.
Solution:
If x = – 8 and y = – 10
Here x > y
x² = (- 8)² = 64 and y² = (- 10)² = 100
But x² > y² is false here. [ ∵ 64 < 100]
(This can be proved for any set of nega-tive numbers or a negative number and a positive number)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 14 Probability Ex 14.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 14th Lesson Probability Exercise 14.1

Question 1.
A die has six faces numbered from 1 to 6. It is rolled and number on the top face is noted. When this is treated as a random trial.
(Random trial: All possible outcomes are known before hand and the exact outcome can’t be predicted, then only the experiment is treated as a random experiment or a trial.)

a) What are the possible outcomes ?
Solution:
The possible outcomes are 1, 2, 3, 4, 5 and 6.

b) Are they equally likely ? Why ?
Solution:
Yes. All the outcomes are equally likely since every event has equal chance of occurrence or no event has priority to occur.

c) Find the probability of a composite number turning up on the top face.
Solution:
Even : Turning up of a composite number
Possible outcomes = 4, 6
No. of possible outcomes = 2
Total outcomes = 1, 2, 3, 4, 5 and 6
Number of total outcomes = 6
Probability = \( \frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }} \\\)
= \(\frac{2}{6}=\frac{1}{3}\)

Question 2.
A coin is tossed 100 times and the following outcomes are recorded. Head : 45 times; Tails : 55 times from the experiment.
a) Compute the probability of each outcome.
Solution:
Head = 45 times; Tails = 55 times
Total = 100
P(H),
Probability of getting Head = \(\frac{45}{100}\)
P(T),
Probability of getting Tail = \(\frac{55}{100}\)
\(\left[P=\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\right]\)

b) Find the sum of the probabilities of all outcomes.
Solution:
P(H) + P(T) = \(\frac{45}{100}+\frac{55}{100}=\frac{100}{100}\) = 1

Question 3.
A spinner has four colours as shown in the figure. When we spin it once, find

a) At which colour, is the pointer more likely to stop ?
Solution:
Red = 5 sectors; Blue = 3 sectors;
Green = 3 sectors; Yellow = 1 sector
Total = 5 + 3 + 3+1 = 12 sectors
∴ Pointer is more likely to stop at Red.

b) At which colour, is the pointer less likely to stop ?
Solution:
Yellow; as only one sector is shaded in Yellow.

c) At which colours, is the pointer equally likely to stop ?
Solution:
Blue and Green have equal chances; as they are shaded in equal number of sectors.

d) What is the chance the pointer will stop on white ?
Solution:
No chance. Since no sector is shaded in white.

e) Is there any colour at which the pointer certainly stops ?
Solution:
No; as the experiment is a random ex-periment.

Question 4.
A bag contains five green marbles, three blue marbles, two red marbles and two yellow marbles. One marble is drawn out randomly. M)
a) Are the four different colour outcomes equally likely ? Explain.
Solution:
No. As they are not in equal number, they have different chances of occurrence.

b) Find the probability of drawing each colour marble, i.e., P (green), P (blue), P(red) and P (yellow).
Solution:

c) Find the sum of their probabilities.
Solution:
P(Green) + P(Blue) + P(Red) +P(Yellow)
= \(\frac{5}{12}+\frac{3}{12}+\frac{2}{12}+\frac{2}{12}\)
= \(\frac{5+3+2+2}{12}=\frac{12}{12}\) = 1

Question 5.
A letter is chosen from English alphabet. Find the probability of the letters being
a) A vowel
b) A letter comes after P
c) A vowel or a consonant
d) Not a vowel
Solution:
Total letters ;= 26 [A, B, C ….. Z]
Probability = \(\frac{\text { No. of favourables }}{\text { Total no. of outcomes }}\)
a) Vowels = a, e, i, o, u [5]
∴ (vowels) = \(\frac{5}{26}\)

b) Letter after P = 10
[Q, R, S, T, U, V, W, X, Y, Z]
Probability of a letter that comes after
’P’ = \(\frac{10}{26}\) = \(\frac{5}{13}\)

c) A vowel or a consonant
Vowel or consonants = 26
[all letters from A to Z]
P(vowel or consonant) = \(\frac{26}{26}\) = 1

d) Not a vowel = 21
[other than A, E, I, O, U]
∴ P(not a vowel) = \(\frac{21}{26}\)

Question 6.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg): 4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98,5.04,5.07,5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Total number of bags = 11
No. of bags with a weight more than 5 kg = 7
[5.05, 5.08, 5.03, 5.06, 5.08, 5.04, 5.07]
∴ Probability = \(\frac{\text { favourable outcomes }}{\text { total outcomes }}\)
P(E) = \(\frac{7}{11}\)

Question 7.
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained is given in the following table.

Find the probabilities of the following events for a driver chosen at random from the city:

i) The driver being in the age group 18-29 years and having exactly 3 accidents in one year.
Solution:
Total number of accidents = (440 + 160 + 110 + 61 + 35 + 505 + 125 + 60 + 22 + 18 +
360 + 45 + 35 + 15 + 9) = 2000
Event: The driver being in the age group (18 – 29) years and having exactly 3 accidents
= 61
P(E) = \(\frac{\text { No. of favourables }}{\text { Total outcomes }}=\frac{61}{2000}\)

ii) The driver being in the age group of 30 – 50 years and having one or more accidents in a year.
Solution:
Favourable outcomes = 125 + 60 + 22 + 18 = 225
Total outcomes = 2000
P(E) = \(\frac{225}{2000}=\frac{9}{80}\)

iii) Having no accidents in the year.
Solution:
Favourable outcomes = 440 + 505 + 360 = 1305
Total outcomes = 2000
P(E) = \(\frac{1305}{2000}=\frac{261}{400}\)

Question 8.
What is the probability that a randomly thrown dart hits the square board in shaded region ( Take π = \(\frac{22}{7}\) and express in percentage )
Solution:

Radius of the circle r = 2 cm
Area of the circle A = πr² = \(\frac{22}{7}\) × 2 × 2 = \(\frac{88}{7}\) cm²
Side of the square = 2 × radius
= 2 × 2 = 4cm
Area of the square = S² = 4 × 4 = 16 cm²
Area of the shaded region = Area of the square – Area of the circle

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.2

Question 1.
Construct AABC in which BC = 7 cm,∠B = 75° and AB + AC =12 cm.
Solution:
A.

Steps:

• Draw a line segment BC = 7 cm.
• Erect ∠B = 75°
• MarkapointDon \(\overrightarrow{\mathrm{BX}}\) suchthat BD = AB + AC.
• Join D, C and draw the perpendicular bisector of \(\overline{\mathrm{CD}}\) meeting BD at A.
• Join A to C to form the ΔABC.

Question 2.
Construct ΔPQR in which QR = 8 cm, ∠B = 60° and AB – AC = 3.5 cm.
Read ∠Q = 60°and PQ – PR = 3.5 cm
Solution:
A.

Steps: I

• Draw QR = 8 cm.
• Construct ∠RQX = 300 at Q.
• Mark a point S on \(\overrightarrow{\mathrm{QX}}\) such that QS = PQ  –  PR = 3.5 cm.
• Join S, R and draw the perpendicular bisector to \(\overline{\mathrm{QR}}\) meeting \(\overrightarrow{\mathrm{QX}}\) at P.
• Join P, R to form the ΔPQR.

Question 3.
Construct ΔXYZ in which ∠Y = 30 °; ∠Z = 60 ° and XY + YZ + ZX = 10 cm.
Solution:
A.

Steps:

• Draw a line segment AB = XY + YZ + ZX = 10 cm.
• Construct ∠BAP = \(\frac { 1 }{ 2 }\) ∠Y at A and ∠ABQ = \(\frac { 1 }{ 2 }\) ∠Z at B meeting at X.
• Draw the perpendicular bisectors to XA and XB meeting \(\overline{\mathrm{AB}}\) at Y and Z respectively.
• Join X to Y and Z to form the ΔXYZ.

Question 4.
Construct a right triangle whose base is 7.5 cm and sum of its hypotenuse and otherside is 15 cm.
Solution:
A.

Steps:

• Draw BC = 7.5 cm.
• Construct ∠CBX = 90°
• Mark a point D on \(\overrightarrow{\mathrm{BX}}\) such that BD = 15 cm.
• Join C, D. ‘
• Draw the perpendicular bisectors of \(\overline{\mathrm{CD}}\) meeting BD at A.
• Join A, C to form the ΔABC.

Question 5.
Construct a segment of a circle on a chord of length 5 cm containing the following angles i) 90° ii) 45° iii) 120°
Solution:
i) 90°
A.

Steps:

• Draw a rough sketch of ∠BAC = 90° and ∠BOC = 180°.
• Draw a line segment BC = 5 cm.
• Draw the perpendicular bisector of BC meeting \(\overline{\mathrm{BC}}\) at O
• Draw an arc of radius OB or OC with centre O.
• Mark any point A on the arc and join it with B and C.
• ∠BAC = 90°

ii) 45°

Steps:

• Draw a line segment BC = 5 cm.
• Construct ABOC such that BC = 5 cm, ∠B = 45° = ∠C.
• Draw a circle segment of radius OB or OC with centre ’O’.
• Mark any point A on the segment and join it with B and C.
• ∠BAC = 45°

iii) 120°

Steps:

• Draw a line segment AB = 5 cm. ,
• Construct ΔAOB in which ∠A = 30°; ∠B = 30°; AB = 5 cm.
• With ‘O’ as centre draw a circle segment.
• On the opposite side make any point C and join it with B and C.
• ∠ACB = 120°

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.1

Question 1.
Construct the following angles at the initial point of a given ray and justify the construction.
a) 90°
Solution:

• Let AB be the given ray.
• Produce BA to D.
• Taking A as centre draw a semi circle with some radius.
• With X and Y as Center draw two intersecting arcs of same radius.

Or

|

• Let \(\overrightarrow{\mathrm{AB}}\) be the given ray.
• With A as centre draw an arc of any radius.
• Mark off two equal arcs from X as shown in the figure with the same radius taken as before.
• Bisect the second segment.
• Join the point of intersection of above arcs, with A.
• ∠BAC is the required right angle.
• Join the point of intersection ‘C’ and ‘A’.
• ∠BAC = 90°

In ΔAXY; ∠YAX = 60° and
in ΔAYC ∠YAC = 30° ∠BAC = 90°

b) 45°
Solution:
Steps:

• Construct 90° with the given ray AB.
• Bisect it from ∠BAD = 45°

Or

Steps:

• Construct ∠BAC = 60°
• Bisect ∠BAC = ∠DAC = 30°
• Bisect ∠DAC such that ∠DAE = ∠FAC = 15°
• ∠BAE=45°

ΔAXZ is equilateral
and ∠YAZ = 15°
∴∠XAY = 45°

Question 2.
Construct the following angles using ruler and compass and verify by measuring them by a protractor.
a) 30°
Solution:

• Construct ∠ABY = 60°
• Bisect ∠ABY = 60°
• Such that ∠ABC = ∠CBY = 30°

b) 22\(\frac{1}{2}^{\circ}\)
Solution:

• Construct ∠ABD = 90°.
• Bisect ∠ABD such that ∠ABC = ∠CBD = 45°
• Bisect ∠ABC such that
  ∠ABE = ∠EBC = 22\(\frac{1}{2}^{\circ}\)

c) 15°
Solution:

Steps of construction : ,

• Construct ∠BAE = 60°
• Bisect ∠BAE such that ∠BAC = ∠CAE = 30°
• Bisect ∠BAC such that ∠BAF = ∠FAC = 15°

d) 75°
Solution:

Steps of construction :

• Construct ∠BAC = 60°
• Construct ∠CAD = 60°
• Bisect ∠CAD such that ∠BAE = 90°
• Bisect ∠CAE such that ∠BAF = 75°

e) 105°
Solution:

Steps of construction:

• Construct ∠ABC = 90°
• Construct ∠CBE = 30°
• Bisect ∠CBE such that the angle formed ∠ABD = 105°

f) 135°
Solution:

Steps of construction:

• Construct ∠ABC = 120°
• Construct ∠CBD = 30°
• Bisect ∠CBD such that the angle formed ∠ABE = 135°

Question 3.
Construct an equilateral triangle, given its side of length of 4.5 cm and justify the constraction.
Solution:
A.

• Draw a line segment AB = 4.5 cm.
• With B and A as centres draw two arcs of radius 4.5 cm meeting at C.
• Join C to A and B.
• ΔABC is the required triangle.

Justification:
In ΔABC
AB = ∠C ⇒ ∠C = ∠B
Also AB = BC ⇒ ∠C = ∠A
Hence ∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∴ ∠A = ∠B = ∠C = \(\frac{180^{\circ}}{3}\) = 60°

Question 4.
Construct an isosceles triangle, given its base and base angle and justify the construction. [Hint: You can take any measure of side and angle]
Solution:
A.

Steps:

• Draw a line segment AB of any given length.
• Construct ∠BAX and ∠ABY at A and B such that ∠A = ∠B.
• \(\overrightarrow{\mathrm{AX}}\) and \(\overrightarrow{\mathrm{BY}}\) will intersect at C.
• ΔABC is the required triangle.

Justification:
Drop a perpendicular CM to AB from C.
Now in ΔAMC and ΔBMC
∠AMC = ∠BMC [Right angle]
∠A = ∠B [Construction]
CM = CM (Common)
∴ ΔAMC ≅ ΔBMC
⇒ AC = BC [CPCT]

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.5 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.5

Question 1.
Find the values of x and y in the figures given below.
i)

Solution:
From the figure x = y [ ∵ angles opp. to opp. to equal sides]
But x + y + 30° = 180°
∴ x + y = 180° – 30° = 150°
⇒ x + y = \(\frac { 150° }{ 2 }\) = 75°

ii)

Solution:
From the figure x° + 110° = 180°
[ ∵ Opp. angles of a cyclic quad, are supplementary]
y + 85°= 180°
∴ x= 180° – 110°; y = 180° – 85°
x = 70°; y = 95°

iii)

Solution:
From the figure x = 90° [angle in a semi-circle]
∴ y = 90° – 50° [∵ angle sum property]
= 40°

Question 2.
Given that the vertices A, B, C of a quadrilateral ABCD lie on a circle. Also ∠A + ∠C = 180°, then prove that the vertex D also lie on the same circle.
Solution:
Given : ∠A + ∠C = 180°
∴ ∠B + ∠D = 360° – 180°
[ ∵ sum of the four angles of a quad. is 360 ].
Now in □ABCD, sum of the pairs of opp. angles is 180°.
∴ □ABCD must be a cyclic quadrilateral, i.e., D also lie on the same circle on which the vertices A, B and C lie. Hence proved.

Question 3.
Prove that a cyclic rhombus is a square.
Solution:

Let □ABCD be a cyclic rhombus,
i.e., AB = BC = CD = DA and
∠A + ∠C = ∠B + ∠D = 180°
But a rhombus is basically a parallelo-gram.

Question 4.
For each of the following, draw a circle and inscribe the figure given. If a poly¬gon of the given type can’t be in-scribed, write not possible.
a) Rectangle
b) Trapezium .
c) Obtuse triangle
d) Non-rectangular parallelogram
e) Acute isosceles triangle
f) A quadrilateral PQRS with PR as diameter.
Solution: