AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.1 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.1
![]()
Question 1.
Construct the following angles at the initial point of a given ray and justify the construction.
a) 90°
Solution:
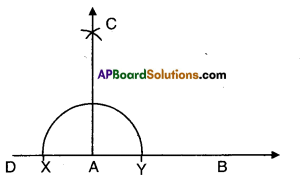
- Let AB be the given ray.
- Produce BA to D.
- Taking A as centre draw a semi circle with some radius.
- With X and Y as Center draw two intersecting arcs of same radius.
Or
 |
|
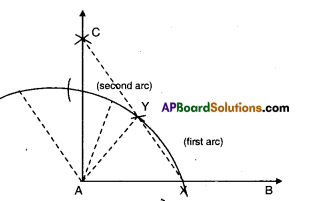
- Let \(\overrightarrow{\mathrm{AB}}\) be the given ray.
- With A as centre draw an arc of any radius.
- Mark off two equal arcs from X as shown in the figure with the same radius taken as before.
- Bisect the second segment.
- Join the point of intersection of above arcs, with A.
- ∠BAC is the required right angle.
- Join the point of intersection ‘C’ and ‘A’.
- ∠BAC = 90°
In ΔAXY; ∠YAX = 60° and
in ΔAYC ∠YAC = 30° ∠BAC = 90°
![]()
b) 45°
Solution:
Steps:
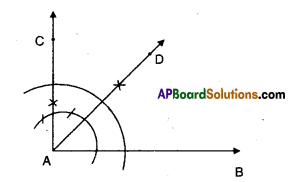
- Construct 90° with the given ray AB.
- Bisect it from ∠BAD = 45°
Or
Steps:
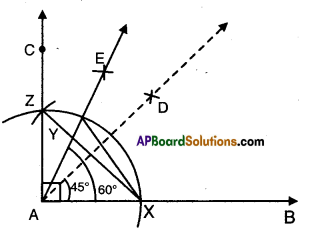
- Construct ∠BAC = 60°
- Bisect ∠BAC = ∠DAC = 30°
- Bisect ∠DAC such that ∠DAE = ∠FAC = 15°
- ∠BAE=45°
ΔAXZ is equilateral
and ∠YAZ = 15°
∴∠XAY = 45°
![]()
Question 2.
Construct the following angles using ruler and compass and verify by measuring them by a protractor.
a) 30°
Solution:
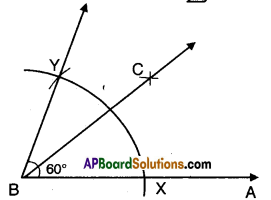
- Construct ∠ABY = 60°
- Bisect ∠ABY = 60°
- Such that ∠ABC = ∠CBY = 30°
b) 22\(\frac{1}{2}^{\circ}\)
Solution:
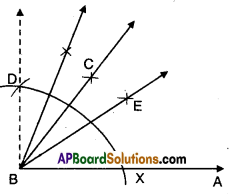
- Construct ∠ABD = 90°.
- Bisect ∠ABD such that ∠ABC = ∠CBD = 45°
- Bisect ∠ABC such that
∠ABE = ∠EBC = 22\(\frac{1}{2}^{\circ}\)
![]()
c) 15°
Solution:
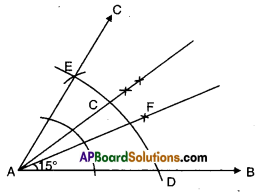
Steps of construction : ,
- Construct ∠BAE = 60°
- Bisect ∠BAE such that ∠BAC = ∠CAE = 30°
- Bisect ∠BAC such that ∠BAF = ∠FAC = 15°
d) 75°
Solution:
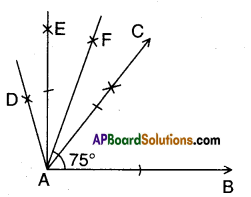
Steps of construction :
- Construct ∠BAC = 60°
- Construct ∠CAD = 60°
- Bisect ∠CAD such that ∠BAE = 90°
- Bisect ∠CAE such that ∠BAF = 75°
![]()
e) 105°
Solution:
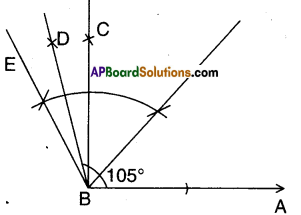
Steps of construction:
- Construct ∠ABC = 90°
- Construct ∠CBE = 30°
- Bisect ∠CBE such that the angle formed ∠ABD = 105°
f) 135°
Solution:
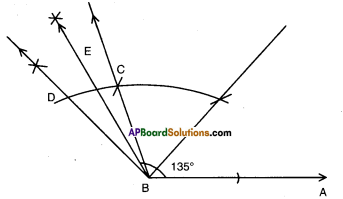
Steps of construction:
- Construct ∠ABC = 120°
- Construct ∠CBD = 30°
- Bisect ∠CBD such that the angle formed ∠ABE = 135°
![]()
Question 3.
Construct an equilateral triangle, given its side of length of 4.5 cm and justify the constraction.
Solution:
A.
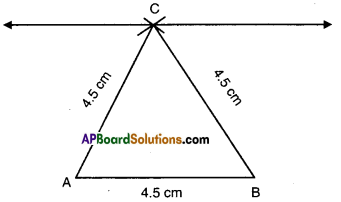
- Draw a line segment AB = 4.5 cm.
- With B and A as centres draw two arcs of radius 4.5 cm meeting at C.
- Join C to A and B.
- ΔABC is the required triangle.
Justification:
In ΔABC
AB = ∠C ⇒ ∠C = ∠B
Also AB = BC ⇒ ∠C = ∠A
Hence ∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∴ ∠A = ∠B = ∠C = \(\frac{180^{\circ}}{3}\) = 60°
![]()
Question 4.
Construct an isosceles triangle, given its base and base angle and justify the construction. [Hint: You can take any measure of side and angle]
Solution:
A.
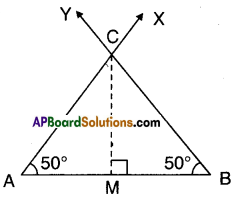
Steps:
- Draw a line segment AB of any given length.
- Construct ∠BAX and ∠ABY at A and B such that ∠A = ∠B.
- \(\overrightarrow{\mathrm{AX}}\) and \(\overrightarrow{\mathrm{BY}}\) will intersect at C.
- ΔABC is the required triangle.
Justification:
Drop a perpendicular CM to AB from C.
Now in ΔAMC and ΔBMC
∠AMC = ∠BMC [Right angle]
∠A = ∠B [Construction]
CM = CM (Common)
∴ ΔAMC ≅ ΔBMC
⇒ AC = BC [CPCT]