Category: Class 6

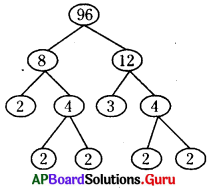
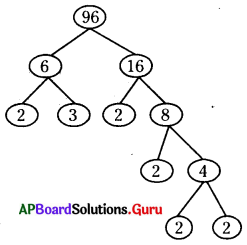
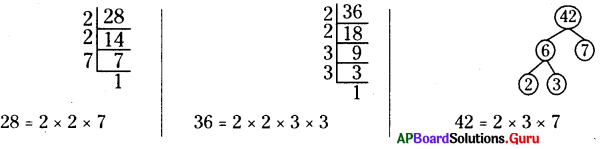AP SCERT 6th Class Maths Textbook Solutions Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson ద్విమితీయ – త్రిమితీయ ఆకారాలు Exercise 9.2

ప్రశ్న 1.
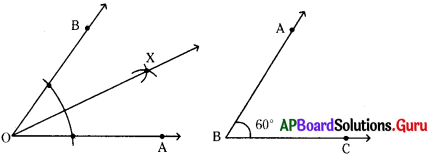
ఇవ్వబడిన త్రిభుజాన్ని గమనించండి మరియు కింది ప్రశ్నలకు జవాబివ్వండి.

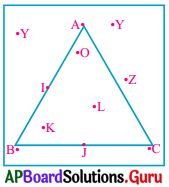
(అ) త్రిభుజానికి బాహ్యంగా ఉండే బిందువులేవి?
(ఆ) త్రిభుజం మీది గల బిందువులేవి?
(ఇ) త్రిభుజానికి అంతరంగా ఉండే బిందువులేవి?
సాధన.
(అ) త్రిభుజానికి బాహ్యంగా గల బిందువులు X, Y, Z.
(ఆ) త్రిభుజం మీది గల బిందువులు A, B, C, I, J.
(ఇ) త్రిభుజానికి అంతరంగా గల బిందువులు O, L, K.

ప్రశ్న 2.
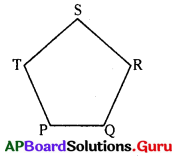
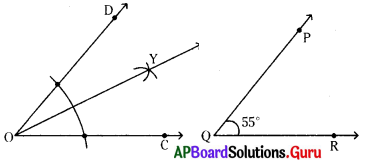
ఇవ్వబడిన త్రిభుజాన్ని గమనించి, కింది ప్రశ్నలకు సమాధానాలివ్వండి.

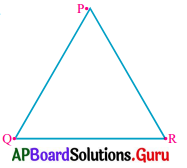
(అ) త్రిభుజంలో ఎన్ని భుజాలు కలవు ? అవి ఏవి?
(ఆ) త్రిభుజంలో ఎన్ని శీర్షాలు ఉన్నవి ? అవి ఏవి?
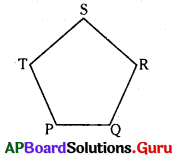
(ఇ) శీర్షం P కు అభిముఖంగా ఉన్న భుజం ఏది?
(ఈ) \(\overline{\mathbf{P R}}\) భుజానికి అభిముఖంగా ఉన్న శీర్షం ఏది?
సాధన.
(అ) 3 భుజాలు కలవు. అవి : (i) \(\overline{\mathbf{P Q}}\) (ii) \(\overline{\mathbf{Q R}}\) (iii) \(\overline{\mathbf{P R}}\).
(ఆ) 3 శీర్షాలు కలవు. అవి : (i) P (ii) Q (iii) R.
(ఇ) శీర్షం P కు అభిముఖంగా ఉన్న భుజం \(\overline{\mathbf{Q R}}\).
(ఈ) \(\overline{\mathbf{P R}}\) భుజానికి అభిముఖంగా ఉన్న శీర్షం ‘Q’.

ప్రశ్న 3.
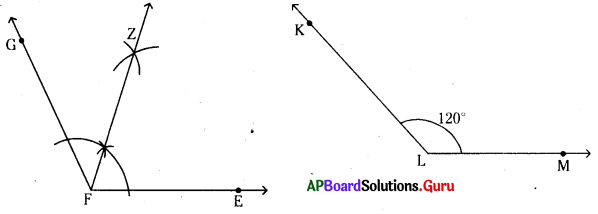
పక్క త్రిభుజాన్ని పరిశీలించి, కింది వాటికి జవాబివ్వండి.

(అ) త్రిభుజంలో గల కోణాలెన్ని ? అవి ఏవి ?
(ఆ) \(\overline{\mathbf{M N}}\) భుజానికి అభిముఖంగా గల కోణమేది?
(ఇ) ఇవ్వబడిన త్రిభుజంలో లంబకోణం కలిగిన శీర్షమేది?
సాధన.
(అ) త్రిభుజంలో గల కోణాల సంఖ్య 3. అవి :
(i) \(\angle \mathrm{MNO}\) లేదా \(\angle \mathrm{N}\),
(ii) \(\angle \mathrm{NOM}\) లేదా \(\angle \mathrm{O}\),
(iii) \(\angle \mathrm{OMN}\) లేదా \(\angle \mathrm{N}\).
(ఆ) \(\overline{\mathbf{M N}}\) భుజానికి అభిముఖంగా గల కోణం \(\angle \mathrm{NOM}\) లేదా \(\angle \mathrm{O}\)
(ఇ) లంబకోణాన్ని కలిగిన శీర్షం ‘O’.

AP SCERT 6th Class Maths Textbook Solutions Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson ద్విమితీయ – త్రిమితీయ ఆకారాలు Exercise 9.1

ప్రశ్న 1.
నాలుగు భుజాలు కలిగియున్న బహుభుజి పేరేమి ? దాని చిత్తు పటం గీయండి.
సాధన.
నాలుగు భుజాలను కలిగిన బహుభుజి చతుర్భుజం.
☐ ABCD ఒక చతుర్భుజం.

ప్రశ్న 2.
పంచభుజి యొక్క చిత్తు పటాన్ని గీయండి.
సాధన.
ఐదు భుజాలను కలిగిన బహుభుజి పంచభుజి.

ప్రశ్న 3.
పక్కన ఇవ్వబడిన ABCDEF బహుభుజి యొక్క భుజాలన్నింటిని రాయండి.
సాధన.

ఇవ్వబడిన బహుభుజి షడ్భుజి.
ABCDEF బహుభుజి యొక్క భుజాలు \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DE}}, \overline{\mathrm{EF}}\) మరియు \(\overline{\text { FA }}\).

ప్రశ్న 4.
PQRST బహుభుజి యొక్క అంతర కోణాలు రాయండి.
సాధన.

PQRST బహుభుజి అంతర కోణాలు

1. \(\angle \mathrm{TPQ}\) లేదా \(\angle \mathrm{P}\)
2. \(\angle \mathrm{PQR}\) లేదా \(\angle \mathrm{Q}\)
3. \(\angle \mathrm{QRS}\) లేదా \(\angle \mathrm{R}\)
4. \(\angle \mathrm{RST}\) లేదా \(\angle \mathrm{S}\)
5. \(\angle \mathrm{STP}\) లేదా \(\angle \mathrm{T}\)

ప్రశ్న 5.
PQRST బహుభుజి భుజాల పొడవులను కొలవండి.
సాధన.

ఇవ్వబడిన బహుభుజి ఐదు భుజాలను కలిగి ఉంటుంది.
అవి : \(\overline{\mathrm{PQ}}\) = 2 సెం.మీ. ; \(\overline{\mathrm{QR}}\) = 2.5 సెం.మీ. ; \(\overline{\mathrm{RS}}\) = 2.4 సెం.మీ.; \(\overline{\mathrm{ST}}\) = 2.2 సెం.మీ., \(\overline{\mathrm{PT}}\) = 2.5 సెం.మీ.

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు InText Questions

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 31]

ప్రశ్న 1.
900, 452, 9534, 788 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా ? ఎందుకు ?
సాధన.
900, 452, 9534, 788 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయి. ఎందుకనగా ఇచ్చిన సంఖ్యల ఒకట్ల స్థానంలో వరుసగా 0, 2, 4, 8లు కలవు.

ప్రశ్న 2.
953, 457, 781, 325, 269 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా ? ఎందుకు ?
సాధన.
953,457, 781, 325, 269 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడవు. ఎందుకనగా ఈ సంఖ్యల ఒకట్ల స్థానంలో 0,2,4,6,8 అంకెలు లేవు.

ప్రశ్న 3.
452, 673, 259, 356 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా? సరిచూడండి.
సాధన.
452, 673, 259, 356 లలో 452 మరియు 356 లు 2 చే నిశ్శేషంగా భాగింపబడతాయి.

673, 259 లు 2చే నిశ్శేషంగా భాగింపబడవు.

[పేజి నెం. 32]

కింది సంఖ్యలు 3 చేత భాగించబడతాయో, లేదో చెప్పండి (భాజనీయతా సూత్రం ఉపయోగించి). భాగహారంతో సరిచూడండి.
అ) 123456
ఆ) 61392
ఇ) 8747
సాధన.
అ) 12345
అంకెల మొత్తం = 1 + 2 + 3 + 4 + 5 = 15
15, 3 చే నిశ్శేషంగా భాగించబడును.
కావున 12345, 3చే నిశ్శేషంగా భాగింపబడుతుంది.
సరిచూడడం :

ఆ) 61392
అంకెల మొత్తం = 6 + 1 + 3 + 9 + 2 = 21
21, 3 చే నిశ్శేషంగా భాగింపబడుతుంది.
కావున 61392, 3 చే నిశ్శేషంగా భాగింపబడుతుంది.
సరిచూడడం :

ఇ) 8747
అంకెల మొత్తం = 8 + 7 + 4 + 7 = 26
26, 3 చే నిశ్శేషంగా భాగింపబడదు.
కావున 8747 ను 3 నిశ్శేషంగా భాగించదు.
సరిచూడడం :

ప్రయత్నించండి [పేజి నెం. 32]

ప్రశ్న 1.
8430 సంఖ్య 6 తో నిశ్శేషంగా భాగింపబడునా ? ఎందుకు?
సాధన.
8430 ని 2 భాగిస్తుంది (ఒకట్ల స్థానంలో ‘0’ కలదు)
అంకెల మొత్తం = 8 + 4 + 3 + 0 = 15
15, 3 చే నిశ్శేషంగా భాగింపబడుతుంది. కావున 8430, 2 మరియు 3 లచే భాగింపబడుతున్నది.
కావున 6 చే కూడా భాగింపబడుతుంది.

ప్రశ్న 2.
ఏవైనా 3 నాలుగంకెల సంఖ్యలను తీసుకొని, అవి 6తో భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
i) 6324, ii) 9314 iii) 7425, iv) 5436 అనే నాలుగు 3 అంకెల సంఖ్యలను తీసుకొందాము.
i) 6324 ను 2 నిశ్శేషంగా భాగిస్తుంది. (ఒకట్ల స్థానం 4 కావున)
6 + 3 + 2 + 4 = 15, 15, 3 చే నిశ్శేషంగా భాగించబడుతుంది.
6324 ను 3 నిశ్శేషంగా భాగిస్తుంది.
6324, 2 మరియు 3చే నిశ్శేషంగా భాగింపబడుతున్నది.
కావున 6 చే భాగింపబడుతుంది.
ii) 9314, 2 చే భాగిస్తుంది. (ఒకట్ల స్థానం 4 కావున)
9 + 3 + 1 + 4 = 17, కావున 3 1 9314 నిశ్శేషంగా భాగింపబడదు.
9314 ను 3 నిశ్శేషంగా భాగింపబడుట లేదు. కావున 6 చే నిశ్శేషంగా భాగింపబడదు.

iii)7425 యొక్క ఒకట్ల స్థానం 5 కావున 7425 ను 2 నిశ్శేషంగా భాగించదు. కావున 6 తో నిశ్శేషంగా భాగింపబడదు.
iv) 5436 యొక్క ఒకట్ల స్థానం 6, అంకెల మొత్తం 5 + 4 + 3 + 6 = 18 కావున 5436 ను 2 మరియు 3లు నిశ్శేషంగా భాగిస్తాయి.
కావున 5436 ను 6 నిశ్శేషంగా భాగిస్తుంది.

ప్రశ్న 3.
6తో భాగింపబడి 2, 3లతో భాగించబడని సంఖ్యకు ఉదాహరణనివ్వగలవా ? ఎందుకు?
సాధన.
6చే భాగింపబడి 2, 3 లతో భాగింపబడని సంఖ్యలకు ఉదాహరణను ఇవ్వలేము.
ఎందుకనగా 6చే భాగింపబడే సంఖ్యలన్నీ 2 మరియు 3లచే భాగింపబడతాయి.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 33]

ప్రశ్న 1.
6669 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుందా ? పరీక్షించండి.
సాధన.
అంకెల మొత్తం = 6 + 6 + 6 + 9 = 27
27, 6 చే నిశ్శేషంగా భాగించబడుతుంది. కావున 6669 సంఖ్య 9చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 2.
భాగహారం చేయకుండానే, 8989794 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుందో, లేదో కనుగొనండి.
సాధన.
ఇచ్చిన సంఖ్యలోని అంకెల మొత్తం = 8 + 9 + 8 + 9 + 7 + 9 + 4 = 54
54 ను 9 నిశ్శేషంగా భాగిస్తుంది. కావున
8989794 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 3.
28570, 90875 సంఖ్యలు 5 చే భాగించబడునా ? భాగహారం చేసి సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్యలు 28570, 90875 సంఖ్యల ఒకట్ల స్థానంలో వరుసగా 0, 5 కలవు కావున ఈ సంఖ్యలు 5 చే నిశ్శేషంగా భాగింపబడతాయి.
సరిచూడటం:

[పేజి నెం. 34]

ప్రశ్న 4.
598, 864, 4782 మరియు 8976 సంఖ్యలు 4 చేత నిశ్శేషంగా భాగించబడునో, లేదో పరిశీలించండి. భాజనీయతా సూత్రంను ఉపయోగించండి మరియు భాగహారంతో సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్యలు 598, 864, 4782 మరియు 8976.
i) 598 లో పదుల, ఒకట్ల స్థానంలోని సంఖ్య 98.
98ని నాలుగు నిశ్శేషంగా భాగించడం లేదు.
కావున 5989 4 నిశ్శేషంగా భాగించదు.
సరిచూచుట :

ii) 864 పదుల, ఒకట్ల స్థానంలోని సంఖ్య = 64.
64 ను 4 నిశ్శేషంగా భాగిస్తుంది.
కావున 864 ను 4 నిశ్శేషంగా భాగిస్తుంది.
సరిచూచుట :

iii) 4782
పదుల, ఒకట్ల స్థానంలోని సంఖ్య 82.
82 ను 4 నిశ్శేషంగా భాగించడం లేదు.
కావున 4782 ను 4 నిశ్శేషంగా భాగించదు.
సరిచూచుట :

iv) 8976
పదుల, ఒకట్ల స్థానంలోని సంఖ్య 76
76 ను 4 నిశ్శేషంగా భాగిస్తుంది.
కావున 8976 ను 4 నిశ్శేషంగా భాగిస్తుంది.
సరిచూచుట :

[పేజి నెం. 35]

ఖాళీలను పూరించి, పట్టికను పూర్తిచేయండి.

పై పట్టిక నుండి ఏమి గమనించారు ?
సాధన.
ప్రతి సందర్భంలో ఈ తేడా ‘0’ లేదా ’11’ యొక్క గుణిజము.
ఈ సంఖ్యలన్నీ 11చే నిశ్శేషంగా భాగింపబడుతాయి.

ప్రయత్నించండి [పేజి నెం. 35]

1221 అనేది “ద్విముఖ సంఖ్య” (పాలి డ్రోమ్ సంఖ్య). ద్విముఖ సంఖ్య అనగా కుడినుండి ఎడమవైపు లేదా ఎడమనుండి కుడివైపు మార్చి రాసినా సంఖ్య మారదు. అందుచే ప్రతి సరి అంకెలు గల్గిన ద్విముఖ సంఖ్య, 11 చే నిశ్శేషంగా భాగింపబడుతుంది. 6 అంకెల ద్విముఖ సంఖ్యను రాయండి.
సాధన.
111111, 222222, 333333, 444444, 555555,
112211, 223322, 334433, 441144, 556655,
122221, 221122, 312213, 423324, 589985,
123321, 231132, 345543, 456654, 576675
142241, 234432, 326623, 478874, 598895
ఇవి అన్నీ 6 అంకెల ద్విముఖ సంఖ్యలు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 37]

ప్రశ్న 1.
60 యొక్క కారణాంకాలు రాయండి.
సాధన.
60 = 1 × 60
60 = 2 × 30
60 = 3 × 20
60 = 4 × 15
60 = 5 × 12
60 = 6 × 10
∴ 60 యొక్క కారణాంకాలు 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

ప్రశ్న 2.
ఒక సంఖ్య యొక్క కారణాంకాలన్నీ ఆ సంఖ్యను నిశ్శేషంగా భాగిస్తాయా ? 30 యొక్క కారణాంకాలను కనుగొనండి. భాగహార పద్ధతి ద్వారా సరిచూడండి.
సాధన.
ఒక సంఖ్య యొక్క కారణాంకాలు అన్నీ ఆ సంఖ్యను నిశ్శేషంగా భాగిస్తాయి.
30 = 1 × 30
30 = 2 × 15
30 = 3 × 10
30 = 5 × 6
30 కారణాంకాలు : 1, 2, 3, 5, 6, 10, 15, 30.


పై భాగహారాలను మనం గమనించినట్లయితే 30 కారణాంకాలైన 1, 2, 3, 5, 6, 10, 15, 30 ల అన్నింటితోను నిశ్శేషంగా భాగింపబడుతున్నది.

ప్రశ్న 3.
15 మరియు 24 యొక్క కారణాంకం 3. ఈ సంఖ్యల భేదానికి కూడా 3 కారణాంకం అవుతుందా?
సాధన.
15 మరియు 24 ల భేదం = 24 – 15 = 9
9 కి 3 కారణాంకం అవుతుంది.

ప్రయత్నించండి [పేజి నెం. 38]

ప్రశ్న 1.
కనిష్ఠ ప్రధాన సంఖ్య ఏది?
సాధన.
2

ప్రశ్న 2.
కనిష్ఠ సంయుక్త సంఖ్య ఏది?
సాధన.
4

ప్రశ్న 3.
కనిష్ఠ బేసి ప్రధాన సంఖ్య ఏది?
సాధన.
3

ప్రశ్న 4.
కనిష్ఠ బేసి సంయుక్త సంఖ్య ఏది?
సాధన.
9

ప్రశ్న 5.
సరి సంయుక్త, బేసి సంయుక్త సంఖ్యలను పదేసి చొప్పున రాయండి.
సాధన.
సరి సంయుక్త సంఖ్యలు : 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.
బేసి సంయుక్త సంఖ్యలు : 9, 15, 21, 25, 27, 33, 35, 39, 45, 49.

ప్రయత్నించండి [పేజి నెం. 39]

ప్రశ్న 1.
రెండంకెల ఒక ప్రధాన సంఖ్యను తిప్పిరాయగా వచ్చిన సంఖ్య కూడా ప్రధాన సంఖ్యే అవుతుందా? ఊహించండి.
(గమనిక : 2 అంకెల సంఖ్యలను తీసుకొని పరిశీలించండి)
సాధన.
రెండంకెల ఒక ప్రధాన సంఖ్యను తిప్పి రాయగా వచ్చిన సంఖ్య కూడా ప్రధాన సంఖ్య కావచ్చును, కాకపోవచ్చును.
ఉదా: 13 ప్రధాన సంఖ్య, 31 కూడా ప్రధాన సంఖ్య.
23 ప్రధాన సంఖ్య, 32 ప్రధాన సంఖ్య కాదు.

ప్రశ్న 2.
311 ప్రధాన సంఖ్య. దీనిలో అంకెలను తారుమారు చేసి మరో రెండు ప్రధాన సంఖ్యలను కనుగొనండి.
సాధన.
113, 131

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 40]

ప్రశ్న 1.
కింద ఇవ్వబడిన సంఖ్యల నుండి సాపేక్ష ప్రధాన సంఖ్యల జతలను గుర్తించండి.
2, 3, 4, 5, 6, 7, 8, 9 మరియు 10.
సాధన.
2, 3, 4, 5, 6, 7, 8, 9 మరియు 10 లలో సాపేక్ష ప్రధాన సంఖ్యల జతలు
(2, 3), (2, 5), (2, 7), (2, 9), (3, 4), (3, 5), (3, 7), (3, 8), (3, 10), (4, 5), (4, 7), (4, 9), (5, 6), (5, 7), (5, 8), (5, 9), (6, 7), (7, 8), (7, 9), (7, 10), (8, 9), (9, 10).

ప్రశ్న 2.
50 కన్నా తక్కువైన కవల ప్రధాన సంఖ్యల జతలను రాయండి.
సాధన.
50 కన్నా తక్కువైన కవల ప్రధానాంకాల జతలు
(3, 5); (5, 7); (11, 13); (17, 19); (29, 31), (41, 43).

[పేజి నెం. 42]

12, 16 మరియు 28 యొక్క గ.సా.భాను కనుగొనండి.
సాధన.

∴ 12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
28 = 2 × 2 × 7
12, 16 మరియు 28 ల ఉమ్మడి కారణాంకం = 2 × 2 = 4
కావున, 12, 16 మరియు 28 ల గ.సా.భా = 4.

ప్రయత్నించండి [పేజి నెం. 43]

ఏవైనా రెండు సంఖ్యల గ.సా.భా ఎంత?
అ) వరుస సంఖ్యలు?
ఆ) వరుస సరి సంఖ్యలు?
ఇ) వరుస బేసి సంఖ్యల గ.సా.భా ఏమవుతుంది? మీరేమి గమనించారు? మీ స్నేహితులతో చర్చించండి.
సాధన.
అ) వరుస సంఖ్యల గ.సా.భా = 1
ఆ) వరుస సరి సంఖ్యల గ.సా.భా = 2 .
ఇ) వరుస బేసి సంఖ్యల గ.సా.భా = 1

గమనించిన అంశాలు :
i) ఏవేని రెండు వరుస సంఖ్యల గ.సా.భా ఎల్లప్పుడు 1.
ii) ఏవేని రెండు వరుస సరిసంఖ్యల గ.సా.భా ఎల్లప్పుడు 2.
iii) ఏవేని రెండు వరుస బేసి సంఖ్యల గ.సా.భా ఎల్లప్పుడు 1.

[పేజి నెం. 45]

ఈ క్రింది వాటి క.సా.గు కనుక్కోండి.
అ) 3, 4
ఆ) 10, 11
ఇ) 10, 30
సాధన.
అ) ఇవ్వబడిన సంఖ్యలు = 3, 4
3 యొక్క కారణాంకాలు = 1 × 3
4 యొక్క కారణాంకాలు = 2 × 2
3, 4 ల యొక్క క.సా.గు = 1 × 3 × 2 × 2 = 12

ఆ) ఇవ్వబడిన సంఖ్యలు = 10, 11
10 యొక్క కారణాంకాలు : 2 × 5
11 యొక్క కారణాంకాలు = 1 × 11
10, 11 ల యొక్క క.సా.గు = 2 × 5 × 11 = 110

ఇ) ఇవ్వబడిన సంఖ్యలు = 10, 30
10 యొక్క కారణాంకాలు = 2 × 5
30 యొక్క కారణాంకాలు = 2 × 3 × 5
10, 30 ల యొక్క క.సా.గు = 2 × 3 × 5 = 30

ఈ) ఇవ్వబడిన సంఖ్యలు = 12, 24
12 యొక్క కారణాంకాలు = 2 × 2 × 3
24 యొక్క కారణాంకాలు = 2 × 2 × 2 × 3
12, 24 ల యొక్క క.సా.గు = 2 × 2 × 2 × 3 = 24

ఉ) ఇవ్వబడిన సంఖ్యలు = 3, 12
3 యొక్క కారణాంకాలు = 1 × 3
12 యొక్క కారణాంకాలు = 2 × 2 × 3
3, 12 ల యొక్క క.సా.గు = 3 × 2 × 2 = 12

[పేజి నెం. 47]

రెండు కవల ప్రధాన సంఖ్యల క.సా.గు మరియు గ.సా.భా ఏమవుతుంది ?
సాధన.
రెండు కవల ప్రధాన సంఖ్యల క.సా.గు మరియు గ.సా.భా = 1

ఉదాహరణలు

ప్రశ్న 1.
6535 సంఖ్య 11 చేత భాగించబడుతుందా ?
సాధన.
బేసి స్థానాలలోని అంకెల మొత్తం = 5 + 5 = 10
సరి స్థానాలలోని అంకెల మొత్తం = 3 + 6 = 9
వాటి తేడా = 10 – 9 = 1
1 సంఖ్య 11 చేత భాగింపబడుతుందా ? కాదు.
కావున, 6535 సంఖ్య 11 చేత భాగించబడదు.

ప్రశ్న 2.
1221 సంఖ్య 11 చేత భాగించబడుతుందా ?
సాధన.
బేసి స్థానాలలోని అంకెల మొత్తం = 1 + 2 = 3
సరి స్థానాలలోని అంకెల మొత్తం = 2 + 1 = 3
వాటి తేడా = 3 – 3 = 0
కావున, 1221 సంఖ్య 11 చేత భాగించబడుతుంది.

ప్రశ్న 3.
100 ను ప్రధాన సంఖ్యల లబ్దంగా రాయండి.
సాధన.
100 = 2 × 50
= 2 × 2 × 25
100 = 2 × 2 × 5 × 5

ప్రశ్న 4.
32 మరియు 40 యొక్క గ.సా.భాను కనుగొనండి.
సాధన.

‘0’ శేషం వచ్చినపుడు చివరి విభాజకం 8.
∴ 32, 40 ల యొక్క గ.సా.భా = 8.

ప్రశ్న 5.
40, 56 మరియు 60 ల యొక్క గ.సా.భా ను కనుగొనండి.
సాధన.
సోపానం – 1: మొదటగా 40 మరియు 56 ల యొక్క గ.సా.భాను కనుగొనాలి.

శేషం ‘0’ అయినపుడు చివరి విభాజకం 8.
∴ 40 మరియు 56 యొక్క గ.సా.భా = 8.

సోపానం – 2: ఇప్పుడు మూడవ సంఖ్యతో మొదటి రెండు సంఖ్యల యొక్క గ.సా.భాతో తిరిగి గ.సా.భాను కనుగొనండి.
అంటే 60 మరియు 8 ల యొక్క గ.సా.భాను కనుగొనండి.

శేషం ‘0’ అయినపుడు చివరి విభాజకం 4.
∴ 60 మరియు 8 ల గ.సా.భా = 4

సోపానం – 3: ఇచ్చిన మూడు సంఖ్యల యొక్క గ.సా.భా = 4.
∴ 40, 56 మరియు 60 యొక్క గ.సా.భా 4.

ప్రశ్న 6.
రెండు ట్యాంకర్లలో వరుసగా 850 లీటర్లు మరియు 680 లీటర్ల కిరోసిన్ ఉన్నది. రెండు ట్యాంకర్లలో ఉన్న కిరోసిన్ ను కొలవగలిగే గరిష్ఠ సామర్థ్యం గల కొలపాత్ర యొక్క సామర్థ్యం ఎంత?
సాధన.
రెండు ట్యాంకర్లలో వున్న కిరోసిన్ ను కొలవగలిగే పాత్ర సామర్థ్యం ట్యాంకర్ల సామర్థ్యాన్ని కచ్చితంగా భాగించే విభాజకం కావాలి. ఈ సామర్థ్యం (విభాజకం) గరిష్ఠంగా ఉండాలి. అనగా కొలపాత్ర యొక్క గరిష్ఠ సామర్థ్యం 850, 680 ల యొక్క గ.సా.భా కావాలి. 850, 680 ల యొక్క గ.సా.భా 170.

అందుచే రెండు ట్యాంకర్లలోని కిరోసినను కొలవగలిగే పాత్ర యొక్క గరిష్ఠ సామర్థ్యం 170 లీటర్లు. మొదటి ట్యాంకర్ లోని కిరోసినను 5 సార్లు, రెండవ ట్యాంకర్ లోని కిరోసిన్ ను 4 సార్లు కొలవగల్గుతుంది.

ప్రశ్న 7.
21, 35 మరియు 42 ల యొక్క క.సా.గును కనుగొనండి.
సాధన.

21, 35, 42 ల యొక్క క.సా.గు 7 × 3 × 5 × 2 = 210.

ప్రశ్న 8.
8 మరియు 12లక.సా.గును కనుగొని, సంబంధాన్ని ఉపయోగించి సంఖ్యల గ.సా.భాను కనుగొనండి.
సాధన.
8 మరియు 12 ల క.సా.గు = 2 × 2 × 2 × 3 = 24
\(\begin{array}{l|ll}
2 & 8, & 12 \\
\hline 2 & 4, & 6 \\
\hline & 2, & 3
\end{array}\)
క.సా.గు × గ.సా.భా = సంఖ్యల లబ్దం అని మనకు తెలుసు

∴ 8 మరియు 12 ల గ.సా.భా = 4

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson ప్రాయోజిక జ్యామితి InText Questions

ప్రయత్నించండి [పేజి నెం. 146]

ఒకే వ్యాసార్ధం గల రెండు వృత్తాలు నిర్మించండి.
(i) రెండు బిందువుల వద్ద ఖండించుకొనేలా నిర్మించండి.
(ii) ఒకే ఒక బిందువు వద్ద స్పర్శించుకొనేలా నిర్మించండి.

సాధన.

(i) P,Q కేంద్రంగా గల వృత్తాలు R, S అనే రెండు బిందువుల వద్ద ఖండించుకొంటున్నాయి.

(ii) U,V కేంద్రాలుగా గల వృత్తాలు X అనే ఒకే బిందువు వద్ద స్పర్శించుకొంటున్నాయి. ఈ సందర్భంలో \(\overline{\mathrm{UX}}\) = \(\overline{\mathrm{XV}}\) అవుతుంది.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 147]

పై రెండు పద్ధతులలోను \(\overline{\mathrm{AP}}\) = \(\overline{\mathrm{BP}}\) పొడవులు కొలవండి. ఏమి గమనించారు?
సాధన.

ఈ నిర్మాణంలో \(\overline{\mathrm{AP}}\) = \(\overline{\mathrm{PB}}\) అని మనం గమనించాము.
∴ AB ని ‘P’ రెండు భాగాలుగా విభజిస్తుంది.

ఆలోచించండి [పేజి నెం. 148]

రేఖాఖండానికి లంబ సమద్విఖండన రేఖ గీచే విధానంలో సోపానం-2లో \(\overline{\mathrm{AB}}\) సగం కంటే తక్కువ పొడవును వ్యాసార్ధంగా తీసుకుంటే ఏం జరుగుతుంది?
సాధన.
రేఖాఖండానికి లంబ సమద్విఖండన రేఖ గీచే విధానంలో సోపానం-2 లో \(\overline{\mathrm{AB}}\) సగం కంటే తక్కువ పొడవును వ్యాసార్ధంగా తీసుకొంటే చాపరేఖలు ఒకదానినొకటి ఖండించుకొనవు.

పేజి నెం. 152

180° , 240° , 300° కోణాలు నిర్మించండి.
సాధన.
(i) \(\angle \mathbf{A O B}\) = 180°

నిర్మాణం :

• కొంత పొడవుతో \(\overrightarrow{\mathrm{OA}}\) కిరణం గీయాలి.
• ‘O’ కేంద్రంగా కొంత వ్యాసార్ధంతో OA ను M వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• M కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని P వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• P కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని Q వద్ద ఖండించేలా మరో చాపం గీయాలి.
• Q కేంద్రంగా మరలా. అదే వ్యాసార్ధంతో రెండవ చాపాన్ని R వద్ద ఖండించేలా మరో చాపం గీయాలి.
• OR (\(\overrightarrow{\mathrm{OB}}\)) లు కలపాలి. \(\angle \mathbf{A O B}\) కావలసిన కోణం .

(ii) \(\angle \mathbf{PQR}\) = 240°

నిర్మాణం :

• కొంత పొడవుతో \(\overrightarrow{\mathrm{QP}}\) కిరణం గీయాలి.
• ‘Q’ కేంద్రంగా కొంత వ్యాసార్ధంతో QP ను A వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• A కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని B వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• B కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని C వద్ద ఖండించేలా మరో చాపం గీయాలి.
• C కేంద్రంగా మరలా అదే వ్యాసార్ధంతో రెండవ చాపాన్ని D వద్ద ఖండించేలా మరో చాపం గీయాలి.
• D కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మూడవ చాపాన్ని E వద్ద ఖండించేలా మరో చాపం గీయాలి.
• QE (\(\overrightarrow{\mathrm{QR}}\)) లు కలపాలి. \(\angle \mathbf{PQR}\) కావలసిన కోణం.

(iii) \(\angle \mathbf{XYZ}\) = 300°

నిర్మాణం :

• కొంత పొడవుతో \(\overrightarrow{\mathrm{YZ}}\) కిరణం గీయాలి.
• Y కేంద్రంగా కొంత వ్యాసార్ధంతో YZను P వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• P కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని Q వద్ద ఖండించేలా ఒక చాపం గీయాలి.
• Q కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని R వద్ద ఖండించేలా మరొక చాపం గీయాలి.
• R కేంద్రంగా మరలా అదే వ్యాసార్ధంతో రెండవ చాపాన్ని ఏ వద్ద ఖండించేలా మరో చాపం గీయాలి.
• S కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మూడవ ఛాపాన్ని T వద్ద ఖండించేలా మరో చాపం గీయాలి.
• T కేంద్రంగా మరలా అదే వ్యాసార్ధంతో నాలుగవ చాపాన్ని U వద్ద ఖండించేలా మరో చాపం గీయాలి.
• YU (\(\overrightarrow{\mathrm{YX}}\)) లు కలపాలి. \(\angle \mathbf{XYZ}\) కావలసిన కోణం .

పేజి నెం. 153

ప్రశ్న 1.
90° కోణం నిర్మించడానికి మరొక పద్ధతి ఆలోచించండి.
(\(\frac {180}{2}\) = 90°, 180° లకు కోణ సమద్విఖండనరేఖ గీయడం ద్వారా నిర్మించండి.)
సాధన.

నిర్మాణ క్రమం :

• \(\angle \mathbf{AOB}\) = 180° కోణాన్ని నిర్మించాలి. (ఒక సరళరేఖ \(\overrightarrow{\mathrm{AB}}\) ని గీయాలి)
• “O” కేంద్రంగా ‘O’ కు ఇరువైపులా ఒకే వ్యాసార్ధంతో \(\overrightarrow{\mathrm{AB}}\) పై చాపరేఖలు గీచి, ఖండన బిందువులు X, Y లను గుర్తించాలి.
• \(\overrightarrow{\mathrm{XY}}\) పొడవులో సగం కన్నా ఎక్కువ వ్యాసార్ధంతో X, Y లు కేంద్రాలుగా \(\overrightarrow{\mathrm{AB}}\) పైన రెండు చాపరేఖలు గీయాలి. ఖండన బిందువును C గా గుర్తించాలి.
• O, C లను కలుపగా మనకు కావలసిన కోణం \(\angle \mathbf{AOC}\) = 90° ఏర్పడినది.

ప్రశ్న 2.
వృత్తలేఖిని సాయంతో 45° కోణాన్ని నిర్మించండి.
సాధన.
1వ పద్ధతి : (60°ల నుండి 30° + 15° నిర్మించడం ద్వారా)

నిర్మాణక్రమం :

• వృత్తలేఖిని సహాయంతో 60° కోణం \(\angle \mathbf{AOB}\) ని గీయాలి.
• \(\angle \mathbf{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం OC ని గీయాలి. ఇపుడు \(\angle \mathbf{AOC}\) = \(\angle \mathbf{COB}\) = 30° అవుతుంది.
• \(\angle \mathbf{COB}\) = 30° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
• ఇపుడు \(\angle \mathbf{COD}\) = \(\angle \mathbf{DOB}\) = 15° కోణాలు ఏర్పడినవి.
• మనకు కావలసిన కోణం \(\angle \mathbf{AOD}\) = 45°, \(\angle \mathbf{AOD}\) = \(\angle \mathbf{AOC}\) + \(\angle \mathbf{COD}\) = 30° + 15° = 45° ఏర్పడినది.

2వ పద్ధతి : (90° లకు కోణ సమద్విఖండన రేఖ నిర్మించడం ద్వారా)

నిర్మాణక్రమం :

• \(\angle \mathbf{AOB}\) = 60°, \(\angle \mathbf{AOC}\) = 120° కోణాలను నిర్మించాలి.
• \(\angle \mathbf{BOC}\) = 60° కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని గీయాలి.
• ఇపుడు \(\angle \mathbf{AOD}\) = \(\angle \mathbf{AOB}\) + \(\angle \mathbf{BOD}\) = 60° + 30° = 90° ఏర్పడినది.
• \(\angle \mathbf{AOD}\) = 90° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OE}}\) ని గీయాలి. మనకు కావలసిన కోణం \(\angle \mathbf{AOE}\) = 45° ఏర్పడినది.

3వ. పద్దతి : (90° లను సరళకోణం నుండి నిర్మించి (మునుపటి సమస్యలో వలె) దాని కోణ సమద్విఖండనం చేయడం ద్వారా నిర్మించవచ్చును.)
4వ పద్దతి : (లంబకోణ సమద్విబాహు త్రిభుజ భావన నుండి)

నిర్మాణక్రమం :

• \(\angle \mathbf{XOY}\) = 90° కోణాన్ని నిర్మించాలి. (పై సమస్యలోవలె)
• O కేంద్రంగా కొంత వ్యాసార్ధంలో \(\overrightarrow{\mathrm{OX}}\) మరియు \(\overrightarrow{\mathrm{OY}}\) లపై చాపరేఖలను గీచి, ఖండన బిందువులు A, B లుగా గుర్తించి, A, B లను కలపాలి.
• కావలసిన కోణం \(\angle \mathbf{OBA}\) = 45° ఏర్పడినది.

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Unit Exercise

ప్రశ్న 1.
భాజనీయతా సూత్రం ప్రకారం ఇచ్చిన సంఖ్యలను వర్గీకరించండి.

సాధన.

ప్రశ్న 2.
11 భాజనీయతా సూత్రంను ఉదాహరణతో రాయండి.
సాధన.
11 భాజనీయతా సూత్రము :
సంఖ్యలోని బేసి స్థానాలలోని అంకెల మొత్తం, సరిస్థానాలలోని అంకెల మొత్తంల తేడా ‘0’ లేదా 11 యొక్క గుణిజం అయిన ఆ సంఖ్య 11 చే నిశ్శేషంగా భాగింపబడుతుంది.
ఉదా :
సంఖ్యను తీసుకొందాం.
బేసి స్థానాలలోని అంకెల మొత్తం = 3 + 4 = 7
సరి స్థానాలలోని అంకెల మొత్తం = 4 + 3 = 7
వీని భేదం = 0
బేసి స్థానాలలోని అంకెల మొత్తం, సరిస్థానాలలోని అంకెల మొత్తంల భేదం ‘0’ కావున 3443ను 11 నిశ్శేషంగా భాగిస్తుంది.

ప్రశ్న 3.
సరైన సమాధానంతో పట్టికను పూరించండి.

సాధన.

ప్రశ్న 4.
ప్రధాన కారణాంక విభజన పధ్ధతి ద్వారా 70, 105 మరియు 175 ల గ.సా.భాను కనుగొనండి.
సాధన.
ఇచ్చిన సంఖ్యలు = 70, 105, 175

70 = 2 × 5 × 7
105 = 3 × 5 × 7
175 = 5 × 5 × 7
70, 105, 175 ల గ.సా.భా = 5 × 7 = 35

ప్రశ్న 5.
భాగహార పద్ధతి ద్వారా 18, 54, 81 ల యొక్క గ.సా.భాను కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్యలు = 18, 54, 81

18, 54 ల గ.సా.భా = 18

8, 81 ల గ.సా.భా = 9
∴ కావున 18, 54, 81 ల గ.సా.భా = 9

ప్రశ్న 6.
రెండు పద్ధతుల ద్వారా 4, 12, 24 ల యొక్క క.సా.గును కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్యలు 4, 12, 24
ప్రధాన కారణాంక విభజన పద్ధతిలో క.సా.గు:
4 = 2 × 2
12 = 2 × 2 × 3
24 = 2 × 2 × 2 × 3
భాగహార పద్ధతిలో క.సా.గు:

క.సా.గు = 2 × 2 × 3 × 1 × 1 × 2 = 24
కనీసం రెండు సంఖ్యలలో ఉమ్మడి కారణాంకాలు = 2, 2, 3
మిగిలిన కారణాంకాలు = 2
∴ క.సా.గు = 2 × 2 × 3 × 2 = 24

ప్రశ్న 7.
మూడు రకాల నూనెలు 32 లీటర్లు, 24 లీటర్లు మరియు 48 లీటర్లు పాత్రలో ఉన్నాయి. మూడింటిని కచ్చితంగా కొలవడానికి కావలసిన కొలతపాత్ర యొక్క గరిష్ఠ ఘనపరిమాణం ఎంత?
సాధన.
మూడు రకాల నూనెల పరిమాణం = 32 లీటర్లు, 24 లీటర్లు, 48 లీటర్లు.
మూడింటిని కచ్చితంగా కొలవడానికి కావలసిన పాత్ర యొక్క గరిష్ఠ ఘనపరిమాణం = 32, 24, 48 ల గ.సా.భా

32, 24 ల గ.సా.భా = 8
8 మరియు 48 ల గ.సా.భా = 8
∴ మూడింటిని ఖచ్చితంగా కొలవడానికి కావలసిన కొలత పాత్ర యొక్క గరిష్ఠ ఘనపరిమాణం = 8 లీటర్లు

ప్రశ్న 8.
రెండు సంఖ్యల గ.సా.భా మరియు క.సా.గులు వరుసగా 9 మరియు 54. ఒక సంఖ్య 18 అయిన రెండవ సంఖ్యను కనుక్కోండి.
సాధన.
రెండు సంఖ్యల గ.సా.భా = 9
మరియు క.సా.గు = 54
అందులో ఒక సంఖ్య = 18
రెండవ సంఖ్య = ?

∴ రెండవ సంఖ్య = 27

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson ప్రాయోజిక జ్యామితి Unit Exercise

ప్రశ్న 1.
X కేంద్రంగా 10 సెం.మీ. వ్యాసం గల ఒక వృత్తం నిర్మించుము.
సాధన.
వ్యాసం = 10 సెం.మీ. కావున వ్యాసార్ధం = 5 సెం.మీ. లతో వృత్తాన్ని గీయాలి.

వ్యా సం AB = 10 సెం.మీ.
వ్యాసార్ధం XB = 5 సెం.మీ.

ప్రశ్న 2.
P కేంద్రంగా 2సెం.మీ., 3 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ., వ్యాసార్ధాలు గల నాలుగు వృత్తాలు గీయుము.
సాధన.
P – వృత్త కేంద్రము. (పై వృత్తాలను ఏకకేంద్ర వృత్తాలు అంటారు.)

3. కోణమానిని ఉపయోగించి కింది కోణాలు నిర్మించండి.

ప్రశ్న (అ)
75°
సాధన.

నిర్మాణక్రమము :

1. కొంత పొడవు గల \(\overrightarrow{\mathrm{OA}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్యబిందువును ‘O’ వద్ద ఉంచి \(\overrightarrow{\mathrm{OA}}\) ఆధారరేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 75° వద్ద B బిందువును గుర్తించాలి.
4. OBలు కలపాలి. \(\angle \mathrm{AOB}\) = 75°

ప్రశ్న (ఆ)
15°
సాధన.
\(\angle \mathrm{PQR}\) = 15°

నిర్మాణ క్రమము :

1. కొంత పొడవు గల \(\overrightarrow{\mathrm{QP}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Q’ వద్ద ఉంచి \(\overrightarrow{\mathrm{QP}}\) ఆధారరేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 15° వద్ద R బిందువును గుర్తించాలి.
4. QR లు కలపాలి. \(\angle \mathrm{PQR}\) = 15.

ప్రశ్న (ఇ)
105°
సాధన.

నిర్మాణక్రమము :

1. కొంత పొడవు గల \(\overrightarrow{\mathrm{YX}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్యబిందువును ‘Y’ వద్ద ఉంచి \(\overrightarrow{\mathrm{YX}}\) ఆధారలేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 105° వద్ద Z బిందువును గుర్తించాలి.
4. YZ లు కలపాలి. \(\angle \mathrm{XYZ}\) = 105° కోణం.

ప్రశ్న 4.
\(\angle \mathrm{ABC}\) = 50° నిర్మించి, దానికి సమానమగు \(\angle \mathrm{XYZ}\) ను కోణమానిని సాయం లేకుండా నిర్మించండి.
సాధన.

\(\angle \mathrm{ABC}\) = 50° మరియు \(\angle \mathrm{XYZ}\) = 50°.

నిర్మాణక్రమం :
1. కోణమానిని ఉపయోగించి \(\angle \mathrm{ABC}\) = 50° కోణాన్ని గీయాలి.
2. B కేంద్రంగా కొంత వ్యాసార్ధంతో \(\overrightarrow{\mathrm{BA}}\) మరియు \(\overrightarrow{\mathrm{BC}}\) కిరణాలపై ఒక చాప రేఖను గీచి, ఖండన బిందువులను P, Q లుగా గుర్తించాలి.
3. \(\overrightarrow{\mathrm{YX}}\) కిరణంపై Y కేంద్రంగా పై తీసుకొన్న వ్యాసార్ధంతో ఒక చాపరేఖను గీయాలి. ఇది \(\overrightarrow{\mathrm{YX}}\) ని R వద్ద ఖండించినది. ఇపుడు R కేంద్రంగా \(\overrightarrow{\mathrm{PQ}}\) వ్యాసార్ధంతో ఇంతకు ముందు గీచిన చాపరేఖను ఖండించాలి. ఖండన బిందువును S గా గుర్తించాలి. Y, S గుండా \(\overrightarrow{\mathrm{YZ}}\) కిరణాన్ని గీయాలి. మనకు కావలసిన \(\angle \mathrm{XYZ}\) = 50° కోణం ఏర్పడినది.

ప్రశ్న 5.
\(\angle \mathrm{DEF}\) = 60° నిర్మించి, దానిని సమద్విఖండన చేయుము. ప్రతి సగాన్ని కోణమానితో కొలవండి.
సాధన.
\(\angle \mathrm{DEF}\) = 60°

\(\angle \mathrm{DEF}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OX}}\).
\(\angle \mathrm{DEF}\) = \(\angle \mathrm{XEF}\) = \(\frac {[latex]\angle \mathrm{DEF}\)}{2}[/latex] = \(\frac {60°}{2}\) = 30°

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.7 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.7

ప్రశ్న 1.
ఈ కింది సంఖ్యల క.సా.గు, గ.సా.భాలను కనుక్కోండి.
అ) 15, 24
ఆ) 8, 25
ఇ) 12, 48
ఈ) 30, 48
వాటి మధ్య గల సంబంధాన్ని సరిచూడండి.
సాధన.
అ) 15, 24

15, 24 ల క.సా.గు = 3 × 5 × 8 = 120
15, 24 ల గ.సా.భా = 3
క.సా.గు × గ.సా.భా = 120 × 3 = 360
15, 24 ల లబ్దం = 15 × 24 = 360
∴ క.సా.గు మరియు గ.సా.భాల లబ్దం = ఆ రెండు సంఖ్యల లబ్దం

ఆ) 8, 25

8, 25 ల క.సా.గు = 2 × 4 × 5 × 5 = 200
8, 25 ల గ.సా.భా = 1
క.సా.గు × గ.సా.భా = 200 × 1 = 200
8, 25 ల లబ్దం = 8 × 25 = 200
∴ క.సా.గు × గ.సా.భా = ఆ రెండు సంఖ్యల లబ్దము

ఇ) 12, 48

12, 48 ల క.సా.గు = 2 × 2 × 2 × 2 × 3 × 1 × 1 = 48
12, 48 ల గ.సా.భా = 12
క.సా.గు × గ.సా.భా = 48 × 12 = 576
12, 48 ల లబ్దం = 12 × 48 = 576
∴ క.సా.గు × గ.సా.భా = ఆ రెండు సంఖ్యల లబ్దం

ఈ) 30, 48

30, 48 ల క.సా.గు = 2 × 3 × 5 × 8 = 240
30, 48 ల గ.సా.భా = 6
క.సా.గు × గ.సా.భా = 6 × 240 = 1440
ఆ రెండు సంఖ్యల లబ్దం = 48 × 30 = 1440
∴ క.సా.గు × గ.సా.భా = ఆ రెండు సంఖ్యల లబ్దం

ప్రశ్న 2.
రెండు సంఖ్యల క.సా.గు 290 మరియు వాటి లబ్దం 7250, అయిన వాటి గ.సా.భా ఎంత?
సాధన.
రెండు సంఖ్యల క.సా.గు = 290
రెండు సంఖ్యల లబ్దం = 7250
వాటి గ.సా.భా = ?
క.సా.గు × గ.సా.భా = రెండు సంఖ్యల లబ్దం

∴ రెండు సంఖ్యల గ.సా.భా = 25

ప్రశ్న 3.
రెండు సంఖ్యల లబ్దం 3276. వాటి గ.సా.భా 6, అయిన వాటి క.సా.గు ఎంత?
సాధన.
రెండు సంఖ్యల లబ్దం = 3276
ఆ రెండు సంఖ్యల గ.సా.భా = 6
వాటి క.సా.గు = ?

ప్రశ్న 4.
రెండు సంఖ్యల గ.సా.భా 6 మరియు వాటి క.సా.గు 36. ఒక సంఖ్య 12, అయిన రెండవ సంఖ్య ఎంత?
సాధన.
రెండు సంఖ్యల గ.సా.భా = 6
ఆ రెండు సంఖ్యల క.సా.గు = 36
ఆ రెండింటి సంఖ్యలలో ఒక సంఖ్య = 12
రెండవ సంఖ్య = ?

∴ రెండవ సంఖ్య = 18

ప్రశ్న 5.
రెండు సంఖ్యల గ.సా.భా 16 మరియు క.సా.గు 384 గా వుండవచ్చా? కారణం రాయండి.
సాధన.
లెక్క ప్రకారం రెండు సంఖ్యల గ.సా.భా = 16
క.సా.గు = 384

క.సా.గు 384 ను గ.సా.భా. 16 నిశ్శేషంగా భాగిస్తున్నది.
కావున రెండు సంఖ్యల గ.సా.భా 16, వాని క.సా.గు 384 గా ఉండవచ్చును.

ప్రశ్న 6.
రెండు సంఖ్యల గ.సా.భా 14 మరియు క.సా.గు 204 గా వుండవచ్చా? కారణం రాయండి.
సాధన.
లెక్క ప్రకారం రెండు సంఖ్యల గ.సా.భా = 14
క.సా.గు = 204

క.సా.గు 204 ను గ.సా.భా 14 నిశ్శేషంగా భాగించడం లేదు.
కావున రెండు సంఖ్యల గ.సా.భా 14 మరియు క.సా.గు 204 గా ఉండదు.

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.6 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.6

1. ప్రధాన కారణాంక విభజన పద్ధతి ప్రకారం కింది సంఖ్యల క.సా.గును కనుగొనండి.
అ) 12 మరియు 15
అ) 15 మరియు 25
ఇ) 14 మరియు 21
సాధన.
అ) 12 మరియు 15
\(\begin{array}{l|l}
2 & 12 \\
\hline 2 & 6 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)

\(\begin{array}{l|l}
3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
12 = 2 × 2 × 3; 15 = 3 × 5
ఉమ్మడి కారణాంకాలు = 3
మిగిలిన కారణాంకాలు = 2 × 2 × 5
∴ 12 మరియు 15 ల క.సా.గు = ఉమ్మడి కారణాంకాలు × మిగిలిన కారణాంకాలు = 3 × 2 × 2 × 5 = 60

ఆ) 15 మరియు 25
\(\begin{array}{l|l}
3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)

\(\begin{array}{c|c}
5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
15 = 3 × 5; 25 = 5 × 5
ఉమ్మడి కారణాంకాలు = 5
మిగిలిన కారణాంకాలు = 3 × 5
∴ 15 మరియు 25 ల క.సా.గు = 5 × 3 × 5 = 75

ఇ) 14 మరియు 21
\(\begin{array}{l|l}
2 & 14 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)

\(\begin{array}{l|l}
3 & 21 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
14 = 2 × 7; 21 = 3 × 7
ఉమ్మడి కారణాంకాలు = 7
మిగిలిన కారణాంకాలు = 2 × 3
14 మరియు 21 ల క.సా.గు = 7 × 2 × 3 = 42

2. భాగహార పద్ధతిని ఉపయోగించి కింది సంఖ్యల క.సా.గును కనుగొనండి.
అ) 84, 112, 196
ఆ) 102, 119, 153
ఇ) 45, 99, 132, 165
సాధన.
అ) 84, 112, 196

∴ 84, 112, 196 ల క.సా.గు = 2 × 2 × 7 × 3 × 4 × 7 = 2352

ఆ) 102, 119, 153

102, 119, 153 ల క.సా.గు = 3 × 17 × 2 × 7 × 3 = 2142

ఇ) 45, 99, 132, 165

45, 99, 132, 165 ల క.సా.గు
= 3 × 3 × 5 × 11 × 4 = 1980

3. ఏ కనిష్ఠ సంఖ్యను 5 కు కలిపిన అది 12, 14 మరియు 18 ల చేత నిశ్శేషంగా భాగించబడునో కనుగొనండి.
సాధన.
12, 14 మరియు 18 ల క.సా.గు

2 × 3 × 2 × 7 × 3 = 252
252 – 5 = 247
12, 14 మరియు 18 ల చేత నిశ్శేషంగా భాగింపబడుటకు 5 కు కలపవలసిన కనిష్ఠ సంఖ్య = 247.

4. ఏ గరిష్ఠ మూడంకెల సంఖ్యను 75, 45 మరియు 60 లచే భాగిస్తే
అ) శేషం సున్న వస్తుంది. ఆ) శేషం ప్రతి సందర్భంలో 4 వచ్చును.
సాధన.
75, 45 మరియు 60 ల క.సా.గు
= 3 × 5 × 5 × 3 × 4 = 900
(900 కన్న పెద్దది మరియు 75, 45, 60 లతో భాగింపబడే సంఖ్య = 900 × 2 = 1800 కాని ఇది నాలుగంకెల సంఖ్య)

అ) 75, 45, 60 లచే భాగిస్తే శేషం ‘0’ వచ్చే గరిష్ఠ మూడంకెల సంఖ్య = 900
ఆ) శేషం ప్రతి సందర్భంలోను 4 వచ్చే గరిష్ఠ మూడంకెల సంఖ్య = 900 + 4 = 904

5. రెండు గంటలు వరుసగా 3 నిమిషాలు మరియు 4 నిమిషాలకు మోగుతాయి. ఒకసారి రెండు గంటలు కలిసి మోగిన తర్వాత, తిరిగి అవి రెండూ కలిసి మోగడానికి ఎంత సమయం పడుతుంది?
సాధన.
3, 4 ల క.సా.గు = 2 × 2 × 3 = 12

ఒకసారి రెండు గంటలు కలిసి మోగిన తర్వాత, తిరిగి అవి రెండూ కలిసి మోగడానికి 12 నిమిషాల సమయం పడుతుంది.

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.4 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.4

ప్రశ్న 1.
కోణమానిని ఉపయోగించకుండా \(\angle \mathrm{ABC}\) = 60° నిర్మించండి.
సాధన.
సోపానం – 1 : ‘l’ రేఖను గీచి దానిపై బిందువు ‘O’ ను గుర్తించాలి.

సోపానం – 2 : వృత్తలేఖిని లోహముల్లు ‘O’ మీద ఉంచి, కొంత వ్యాసార్ధంతో l ను A వద్ద ఖండించినట్లు ఒక చాపం గీయాలి.

సోపానం – 3 : A కేంద్రంగా సోపానం 2 లోని వ్యాసార్ధంతో పై చాపాన్ని B వద్ద ఖండించేలా మరో చాపం గీయాలి.

సోపానం – 4 : OB లు కలపాలి. 60° కొలత గల \(\angle \mathrm{BOA}\) ఏర్పడింది.

ప్రశ్న 2.
కోణమానిని మరియు వృత్తలేఖినిల సాయంతో 120° కోణం నిర్మించండి.
సాధన.
సోపానం – 1: OA కిరణం గీయాలి.

సోపానం – 2 : 0 కేంద్రంగా కొంత వ్యాసార్ధంతో OA ను M వద్ద ఖండించేలా ఒక చాపం గీయాలి.

సోపానం – 3 : M కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని P వద్ద ఖండించేలా మరో చాపం గీయాలి.

సోపానం – 4 : P కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని Q వద్ద ఖండించేలా మరో చాపం గీయాలి.

సోపానం – 5 : OQ లు కలపాలి. \(\angle \mathrm{AOQ}\) కావలసిన కోణం.

3. వృత్తలేఖిని, స్కేలు సాయంతో క్రింది కోణాలు నిర్మించి, నిర్మాణక్రమం రాయండి.

ప్రశ్న (అ)
75°
సాధన.

75° (60 + 15) :
\(\angle \mathrm{AOX}\) = 75°
\(\angle \mathrm{AOC}\) + \(\angle \mathrm{COX}\) = 60° + 15° = 75° .

నిర్మాణక్రమం :

• \(\angle \mathrm{AOC}\) = 60° మరియు \(\angle \mathrm{AOB}\) = 120° కోణాలను పై 2వ సమస్యలో వలె నిర్మించాలి.
• \(\angle \mathrm{COB}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
• ఇప్పుడు \(\angle \mathrm{AOD}\) = 90° (\(\angle \mathrm{AOC}\) + \(\angle \mathrm{COD}\) = 60° + 30° = 90°)
• \(\angle \mathrm{COD}\) = 30° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OX}}\) ని నిర్మించాలి.
• మనకు కావలసిన కోణం \(\angle \mathrm{AOX}\) = \(\angle \mathrm{AOC}\) + \(\angle \mathrm{COX}\) = 60° + 15° = 75° ఏర్పడినది.

ప్రశ్న (ఆ)
15°
సాధన.

నిర్మాణక్రమం :

• \(\angle \mathrm{AOB}\) = 60° కోణాన్ని నిర్మించాలి.
• \(\angle \mathrm{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం
• \(\overrightarrow{\mathrm{OC}}\) ని నిర్మించాలి.
• \(\angle \mathrm{AOC}\) = \(\angle \mathrm{COB}\) = 30° అవుతుంది.
• \(\angle \mathrm{AOC}\) యొక్క కోణ’ సమద్విఖండన కిరణం
• \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
• ఇప్పుడు మనకు కావలసిన కోణం \(\angle \mathrm{AOD}\) = \(\frac {30°}{2}\) = 15° ఏర్పడినది.

ప్రశ్న (ఇ)
105°
సాధన.
105° (90° + 15° = 105°) :

\(\angle \mathrm{AOE}\) = 105°
\(\angle \mathrm{AOB}\) + \(\angle \mathrm{BOD}\) + \(\angle \mathrm{DOE}\) = 60°+ 30° + 15° = 105°

నిర్మాణ క్రమం :

• \(\angle \mathrm{AOB}\) = 60° మరియు \(\angle \mathrm{AOC}\) = 120° ల కోణాలను నిర్మించాలి.
• \(\angle \mathrm{BOC}\) = 60° యొక్క కోణ సమద్విఖండన కిరణం
• \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
• ఇప్పుడు \(\angle \mathrm{AOD}\) = \(\angle \mathrm{AOB}\) + \(\angle \mathrm{BOD}\) = 60° + 30° = 90° అవుతుంది. అలాగే \(\angle \mathrm{DOC}\) = 30°
• \(\angle \mathrm{DOC}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OE}}\) ని నిర్మించాలి.
• ఇప్పుడు \(\angle \mathrm{DOE}\) = \(\frac {30°}{2}\) = 15° అవుతుంది.
• కావలసిన కోణం \(\angle \mathrm{AOE}\) = \(\angle \mathrm{AOD}\) + \(\angle \mathrm{DOE}\) = 90° + 15° = 105° ఏర్పడినది.

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.3 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.3

1. కోణమానిని సాయంతో కింది కోణాలు నిర్మించండి.

ప్రశ్న (అ)
\(\angle \mathbf{A B C}\) = 65°
సాధన.

నిర్మాణము :
1. కొంత పొడవు గల \(\overrightarrow{\mathrm{BC}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘B’ వద్ద ఉంచి \(\overrightarrow{\mathrm{BC}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 65° వద్ద ‘A’ బిందువును గుర్తించాలి.
4. BA లు కలపాలి. \(\angle \mathbf{A B C}\) = 65°.

ప్రశ్న (ఆ)
\(\angle \mathbf{P Q R}\) = 136°
సాధన.

నిర్మాణము :
1. కొంత పొడవు గల \(\overrightarrow{\mathrm{QR}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Q’ వద్ద ఉంచి \(\overrightarrow{\mathrm{QR}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 136° వద్ద ‘P’ బిందువును గుర్తించాలి.
4. PQలు కలపాలి. \(\angle \mathbf{P Q R}\) = 136°.

ప్రశ్న (ఇ)
\(\angle \mathbf{Y}\) = 45°
సాధన.

నిర్మాణము :
1. కొంత పొడవు గల \(\overline{\mathrm{YZ}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Y’ వద్ద ఉంచి \(\overline{\mathrm{YZ}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 45° వద్ద ‘X’ బిందువును గుర్తించాలి.
4. YXలు కలపాలి. \(\angle \mathrm{XYZ}\) = 45°.

ప్రశ్న (ఈ)
\(\angle \mathbf{O}\) = 172°
సాధన.

నిర్మాణము :
1. కొంత పొడవు గల \(\overline{\mathrm{OT}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘O’ వద్ద ఉంచి \(\overline{\mathrm{OT}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 172° వద్ద ‘D’ బిందువును గుర్తించాలి.
4. OD లు కలపాలి. \(\angle \mathrm{DOT}\) = 172°.

ప్రశ్న 2.
కింది కోణాలను నీ నోట్ పుస్తకంలో కాపీ చేసి, వాటి కోణ సమద్విఖండన కిరణాలు గీయండి.

సాధన.
(i)

\(\angle \mathrm{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OX}}\).
\(\angle \mathrm{AOX}\) = \(\angle \mathrm{XOB}\)

(ii)

\(\angle \mathrm{COD}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OY}}\).
\(\angle \mathrm{COY}\) = \(\angle \mathrm{YOD}\)

(iii)

\(\angle \mathrm{EFG}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{FZ}}\).
\(\angle \mathrm{EFZ}\) = \(\angle \mathrm{ZFG}\)

(iv)

\(\angle \mathrm{PQR}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{QT}}\)
\(\angle \mathrm{PQT}\) = \(\angle \mathrm{TQR}\)

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.5 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.5

ప్రశ్న 1.
కింద ఇవ్వబడిన సంఖ్యల గ.సా.భాను ప్రధాన కారణాంక విభజన పద్ధతి ద్వారా మరియు నిరంతర భాగహార పద్ధతి ద్వారా కనుగొనుము.
అ) 48, 64
ఆ) 126, 216
ఇ) 40, 60, 56
ఈ) 10, 35, 40
సాధన.
అ) 48, 64
ప్రధాన కారణాంక విభజన పద్ధతి :
\(\begin{array}{c|c}
2 & 48 \\
\hline 2 & 24 \\
\hline 2 & 12 \\
\hline 2 & 06 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)

\(\begin{array}{l|l}
2 & 64 \\
\hline 2 & 32 \\
\hline 2 & 16 \\
\hline 2 & 08 \\
\hline 2 & 4 \\
\hline 2 & 2 \\
\hline & 1
\end{array}\)
48 = 2 × 2 × 2 × 2 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2
(48, 64)ల ఉమ్మడి కారణాంకాలు 2,2,2,2
∴ 48, 64 ల గ.సా.భా = 2 × 2 × 2 × 2 = 16

నిరంతర భాగహార పద్ధతి :

శేషం ‘0’ వచ్చినపుడు చివరి భాజకం 16.
∴ 48, 64 గ.సా.భా = 16

ఆ) 126, 216
ప్రధాన కారణాంక విభజన పద్ధతి :
\(\begin{array}{l|l}
2 & 126 \\
\hline 3 & 063 \\
\hline 3 & 21 \\
\hline 7 & 07 \\
\hline & 1
\end{array}\)

\(\begin{array}{l|r}
2 & 216 \\
\hline 2 & 108 \\
\hline 2 & 054 \\
\hline 3 & 27 \\
\hline 3 & 09 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
126 = 2 × 3 × 3 × 7
216 = 2 × 2 × 2 × 3 × 3 × 3
126, 216 ల గ.సా.భా = 2 × 3 × 3 = 18

నిరంతర భాగహార పద్ధతి :

126, 216 ల గ.సా.భా = 18

ఇ) 40, 60, 56
ప్రధాన కారణాంక విభజన పద్ధతి :

40 = 2 × 2 × 2 × 5
60 = 2 × 2 × 3 × 5
56 = 2 × 2 × 2 ×7
40,60,56 ల ఉమ్మడి కారణాంకాలు 2, 2
∴ 40,60,56 ల గ.సా.భా = 2 × 2 = 4

నిరంతర భాగహార పద్ధతి :

40, 60 ల గ.సా.భా = 20
ఇపుడు 20, 56 ల గ.సా.భా

20, 56 ల గ.సా.భా = 4
∴ 40, 60, 56 ల గ.సా.భా = 4

ఈ) 10, 35, 40
ప్రధాన కారణాంక విభజన పద్ధతి :

10 = 2 × 5
35 = 5 × 7
40 = 2 × 2 × 2 × 5
ఉమ్మడి కారణాంకం = 5
10, 35, 40 ల గ.సా.భా = 5

నిరంతర భాగహార పద్ధతి :

10, 35 ల గ.సా.భా = 5

5, 40 ల గ.సా.భా = 5
∴ 10, 35, 40 ల గ.సా.భా = 5.

ప్రశ్న 2.
రెండు పాలక్యాన్లలో వరుసగా 60 లీటర్లు, 165 లీటర్ల పాలు ఉన్నవి. రెండు క్యాన్లలోని పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యానను కనుగొనండి.
సాధన.
రెండు పాలక్యాన్లలో గల పాలు = 60 లీటర్లు మరియు 165 లీటర్లు
రెండు క్యాన్లలోని పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యాన్ = 60, 165 ల గ.సా.భా.

60, 165 ల గ.సా.భా = 15
∴ పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యాన్ = 15 లీటర్లు.

ప్రశ్న 3.
మూడు వేర్వేరు కొలతలు గల కంటైనర్లలో వరుసగా 403 లీటర్లు, 465 లీటర్లు, 527 లీటర్లు పరిమాణాలలో పాలు ఉన్నవి. వేర్వేరు పరిమాణాలలో గల కంటైనర్లలోని పాలను పూర్తిగా కొలవగలిగే గరిష్ఠ పరిమాణం గల కొలత ఎంత?
సాధన.
మూడు కంటైనర్లలో గల పాల పరిమాణం = 403 లీటర్లు, 465 లీటర్లు, 527 లీటర్లు
కంటైనర్లలోని పాలను పూర్తిగా కొలవగలిగే
గరిష్ట పరిమాణం గల కొలత = 403, 465, 527 ల గ.సా.భా = 31

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.4 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.4

ప్రశ్న 1.
90 యొక్క కారణాంక వృక్షాన్ని తయారు చేయండి.
సాధన.

90 = 2 × 3 × 3 × 5

ప్రశ్న 2.
భాగహార పద్ధతిలో 84 ను ప్రధాన కారణాంకాల లబ్ధంగా రాయండి.
సాధన.
84 = 2 × 2 × 3 × 7

ప్రశ్న 3.
4 అంకెల గరిష్ఠ సంఖ్యను రాసి, దానిని ప్రధాన కారణాంకాల లబ్దంగా రాయండి.
సాధన.
4 అంకెల గరిష్ఠ సంఖ్య : 9999


∴ 9999 = 3 × 3 × 11 × 101

ప్రశ్న 4.
కారణాంక వృక్ష పద్ధతి ద్వారా 96 యొక్క ప్రధాన కారణాంక విభజనను రాయండి.
సాధన.

(లేదా)

∴ 96 = 2 × 2 × 2 × 2 × 2 × 3

ప్రశ్న 5.
నేను ఒక కనిష్ఠ సంఖ్యను నేను నాలుగు విభిన్న ప్రధాన కారణాంకాల లబ్దాన్ని నేనెవరో కనుగొనండి.
సాధన.
మొదటి నాలుగు ప్రధాన సంఖ్యలు = 2, 3, 5, 7.
వాటి లబ్ధం = = 210
కావున, నాలుగు విభిన్న ప్రధాన కారణాంకాల లబ్ధంగా గల కనిష్ఠ సంఖ్య = 210.

ప్రశ్న 6.
భాగహార పద్దతిన 28 మరియు 36 ల ప్రధాన కారణాంక విభజనను రాయండి. 42 యొక్క ప్రధాన కారణాంక విభజనను కారణాంక వృక్ష పద్ధతి ద్వారా రాయండి.
సాధన.