Category: Class 10

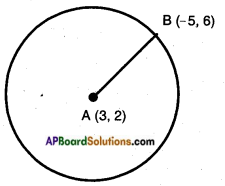
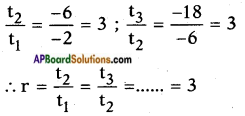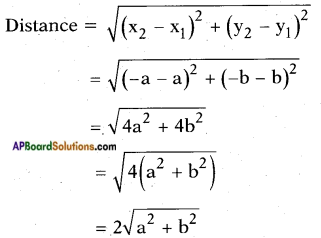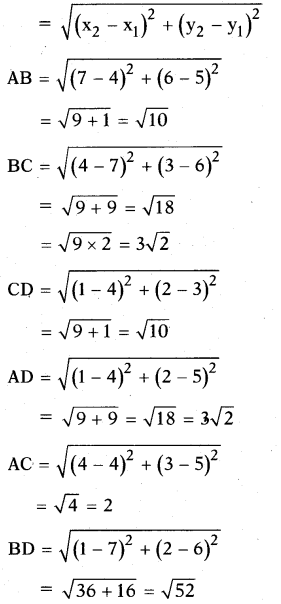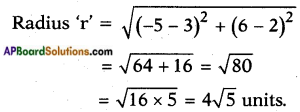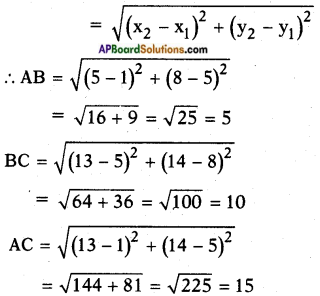AP State Syllabus SSC 10th Class Maths Solutions 12th Lesson Applications of Trigonometry Optional Exercise

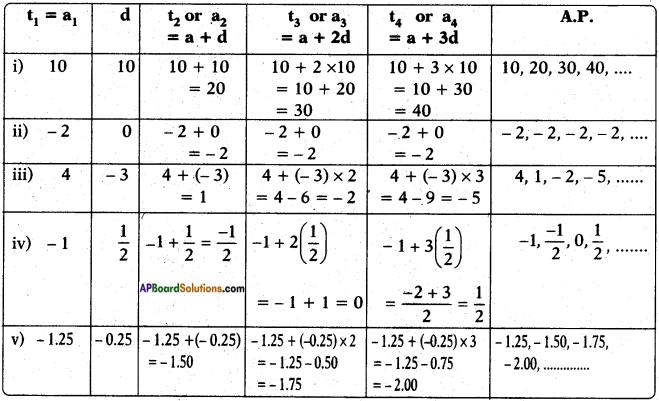
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 12 Applications of Trigonometry Optional Exercise Textbook Questions and Answers.

10th Class Maths 12th Lesson Applications of Trigonometry Optional Exercise Textbook Questions and Answers

Question 1.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.
Answer:
Height of the balloon from the ground = 88.2 m
Height of the girl = 1.2 m
Angles of elevations = 60° and 30°

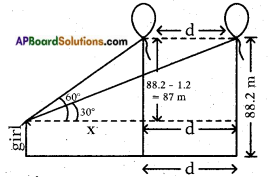
Let the distance travelled = dm
From the figure
tan 60° = [latex]\frac{87}{x}[/latex]
√3 = [latex]\frac{87}{x}[/latex]
⇒ 87 = √3x …….(1)
⇒ x = [latex]\frac{87}{\sqrt{3}}[/latex] m
Also tan 30° = [latex]\frac{87}{x+d}[/latex]
⇒ [latex]\frac{1}{\sqrt{3}}[/latex] = [latex]\frac{87}{x+d}[/latex]
⇒ 87 = [latex]\frac{x+d}{\sqrt{3}}[/latex] ………(2)
From equations (1) and (2)
√3x = [latex]\frac{x+d}{\sqrt{3}}[/latex]
√3 × √3x = x + d
⇒ 3x = x + d
⇒ 2x = d

Question 2.
The angle of elevation of the top of a tower from the foot of the building is 30° and the angle of elevation of the top of the building from the foot of the tower is 60°. What is the ratio of heights of tower and building?
Answer:

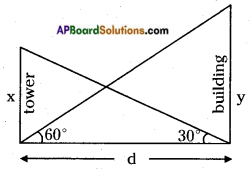
Let the height of the tower = x m
Let the height of the building = y m
Distance between the tower and building = d m.
Angle of elevation of the top of the tower = 30°.
From the figure,

∴ x : y = 1 : 3
∴ The ratio of heights of tower and building = 1 : 3.

Question 3.
The angles of elevation of the top of a lighthouse from 3 boats A, B and C in a straight line of same side of the light- house are a, 2a, 3a respectively. If the distance between the boats A and B is x meters. Find the height of lighthouse.
Answer:
From the figure,

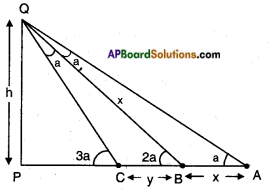
Let PQ be the height of the lighthouse = h m
A = First point of observation
B = Second point of observation
C = Third point of observation Given,
AB = x and BC = y
(Not given in the text)
Exterior angle = Sum of the opposite interior angles
∠PBQ = ∠BQA + ∠BAQ and
∠PCQ = ∠CBQ + ∠CQB
∴ AB = x = OB
By applying the sine rule,

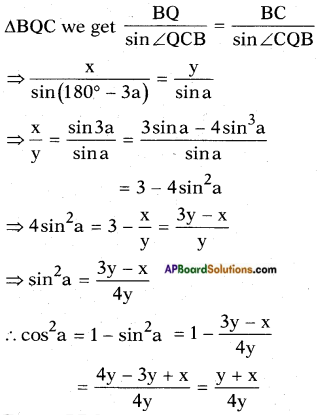
From △PBQ

Question 4.
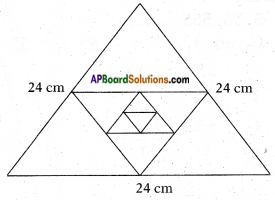
Inner part of a cupboard is in the cuboidical shape with its length, breadth and height in the ratio 1 : √2 : 1. What is the angle made by the longest stick which can be inserted cupboard with its base inside?
Answer:

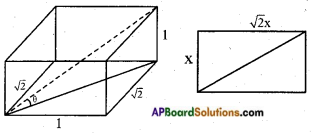
The ratio of the length, breadth and height = 1 : √2 : 1
Let its length be = x
breadth = √2x height = x
The longest stick that can be placed on the base is along its hypotenuse

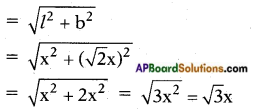
[!! Again, the longest stick that can be inserted in the cup board is along the line join of the bottom corn on with’ its opposite top corner, i.e., along the hypotenuse of the right triangle formed by height of the cup board, hypotenuse of the base and the line join of bottom corner with its opposite top corner.

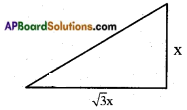
Length of the largest stick = [latex]\sqrt{(\sqrt{3} x)^{2}+x^{2}}[/latex]
= [latex]\sqrt{3 x^{2}+x^{2}}[/latex]
= [latex]\sqrt{4 x^{2}}[/latex] = 2x]
Now the angle made by the largest stick be = θ

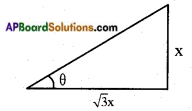
Then tan θ = [latex]\frac{\text { opp. side }}{\text { adj. side }}[/latex] = [latex]\frac{x}{\sqrt{3} x}[/latex] = [latex]\frac{1}{\sqrt{3}}[/latex]
tan θ = tan 30°
∴ θ = 30°.

Question 5.
An iron spherical ball of volume 232848 cm³ has been melted and converted into a cone with the vertical angle of 120°. What are its height and base?
Answer:
Volume of the spherical ball = Volume of the cone

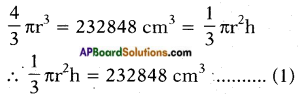
Given that vertical angle = 60°

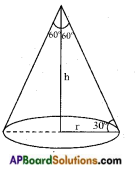
Let its height be h cm. and radius r cm.
From the figure
Also tan 30° = [latex]\frac{h}{r}[/latex]
⇒ [latex]\frac{1}{\sqrt{3}}[/latex] = [latex]\frac{h}{r}[/latex]
∴ h = [latex]\frac{r}{\sqrt{3}}[/latex]
Substituting h = [latex]\frac{r}{\sqrt{3}}[/latex] equation (1) we get

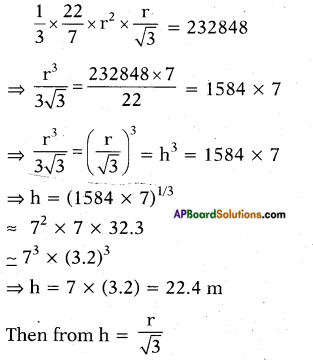
⇒ r = h√3 = (22.4) (1.732) = 38.79 m
r = 38.79 cm and h = 22.4 cm.

AP State Syllabus SSC 10th Class Maths Solutions 3rd Lesson Polynomials InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 3 Polynomials InText Questions and Answers.

10th Class Maths 3rd Lesson Polynomials InText Questions and Answers

Do these

Question 1.
State which of the following are polynomials and which are not? Give reasons.   (Page No. 48)
(i) 2x³
(ii) [latex]\frac{1}{x-1}[/latex]
(iii) 4z² + [latex]\frac{1}{7}[/latex]
(iv) m² – √2 m + 2
(v) p^-2 + 1
Answer:
i) 2x³ is a polynomial.
ii) [latex]\frac{1}{x-1}[/latex] is not a polynomial because its power is negative integer exponent.
iii) 4z² + [latex]\frac{1}{7}[/latex] is a polynomial.
iv) m² – √2 m + 2 is a polynomial.
v) p^-2 + 1 is not a polynomial because its power is negative integer exponent.

Question 2.
p(x) = x² – 5x – 6, find the values of p(l), p(2), p(3), p(0), p(-l), p(-2), p(-3).    (Page No. 49)
Answer:
Given polynomial p(x) = x² – 5x – 6
p(1) = (1)² – 5(1) – 6 = 1 – 5 – 6 = – 10
p(2) = (2)² – 5(2) – 6 = 4 – 10 – 6 = -12
p(3) = 3² – 5(3) – 6 = 9 – 15 – 6 = – 12
p(0) = 0² – 5(0) – 6 = – 6
p(-1) = (-1)² – 5(-1) – 6 = 1 + 5 – 6 = 0
p(-2) = (-2)² – 5(-2) – 6 = 4 + 10 – 6 = 8
p(-3) = (-3)² – 5(-3) – 6 = 9 + 15 – 6 = 18

Question 3.
p(m) = m² – 3m + 1, find the values of p(1)and p(-1).    (Page No. 49)
Answer:
Given polynomial p(m) = m² – 3m + 1
p(1) = (1)² – 3(1) + 1 = 1 – 3 + 1 = 2 – 3 = – 1
p(-1) = (-1)² – 3(-1) + 1 = 1 + 3 + 1 = 5

Question 4.
Let p(x) = x² – 4x + 3. Find the values of p(0), p(l), p(2), p(3) and obtain zeroes of the polynomial p(x).   (Page No. 50)
Answer:
Given polynomial p(x) = x² – 4x + 3
p(0) = (0)² – 4(0) + 3 = 3
p(1) = (1)² – 4(1) + 3 = 1 – 4 + 3 = 0
p(2) = (2)² – 4(2) + 3 = 4 – 8 + 3 = – 1
p(3) = (3)² – 4(3) + 3 = 9 – 12 + 3 = 0
We see that p(1) and p(3) are zeroes of the polynomial p(x).

Question 5.
Check whether -3 and 3 are the zeroes of the polynomial x² – 9.    (Page No. 50)
Answer:
Given polynomial p(x) = x² – 9
Zero of the polynomial p(x) = 0
x² – 9 = 0
⇒ x² = 9
⇒ x = V9 = ± 3
∴ x = + 3, – 3
∴ Zeroes of the polynomial p(x) are – 3 and 3.

Try these

Question 1.
Write 3 different quadratic, cubic and 2 linear polynomials with different number of terms. (Page No. 48)
Answer:
Quadratic polynomials:

Cubic polynomials :

Linear polynomials :
f(t) = √2 t + 5
g(u) = [latex]\frac{2}{3}[/latex] u – [latex]\frac{5}{2}[/latex] and
q(y) = 3y
Yes, we can write polynomials of any degree.

Question 2.
Write a quadratic polynomial and a cubic polynomial in variable x in the general form. (Page No. 49)
Answer:
General form of a quadratic polynomial having variable ‘x’ is
f(x) = ax³ + bx² + c, a ≠ 0
General form of a cubic polynomial having variable ‘x’ is
f(x) = ax³ + bx² + cx + d, a ≠ 0

Question 3.
Write a general polynomial q(z) of degree n with coefficients that are b₀…. b_n. What are the conditions on b₀…. b_n. (Page No. 49)
Answer:
q(z) = b₀zⁿ + b₁z^n-1 + b₂z^n-2 …….. + b_n-1z + b_n is a polynomial of n degree where b₀, b₁, b₂,…… b_n-1, b_n are real coefficients and b₀ ≠ 0.

Do this

Question 1.
Draw the graph of i) y = 2x + 5, ii) y = 2x – 5, iii) y = 2x and find the point of intersection on X – axis. Is the x-coordinates of these points also the zero of the polynomial?   (Page No. 52)
Answer:
i) Given that y = 2x + 5


Result: The graph y = 2x + 5 cuts the X – axis at the point (-2.5, 0).
Hence, the zeroes of the polynomial is -2.5.

ii) Given that y = 2x – 5


Result: The graph of y = 2x – 5 cuts the X – axis at the point (2.5, 0).
The zeroes of the polynomial is 2.5 = [latex]\frac{5}{2}[/latex]

iii) Given that y = 2x


Result: The graph passes through the origin.
So, the zeroes of the polynomial y = 2x is zero.

Try these

Question 1.
Draw the graphs of (i) y = x² – x – 6 (ii) y = 6 – x – x² and find zeroes in each case. What do you notice? (Page No. 53)
Answer:
i) Given that y = x² – x – 6


Result: From the graph we observe that 3 and -2 are the intersecting points of X – axis.
So, the zeroes of given quadratic polynomial are 3 and -2.

ii) Given that y = 6 – x – x²


Result: From the graph we observe that – 3 and 2 are the intersecting points ol X – axis.
So, the zeroes of given quadratic polynomial are – 3 and 2.

Question 2.
Write three quadratic polynomials that have 2 zeroes each.   (Page No. 55)
Answer:
y = x² – x – 2 having two zeroes, i.e., (2, 0) and (- 1, 0).
y = 3 – 2x – x² having two zeroes i.e., (1,0) and (- 3, 0).
y = x² – 3x – 4 having two zeroes i.e., (-1, 0) and (4, 0)

Question 3.
Write one quadratic polynomial that has one zero. (Page No. 55)
Answer:
Quadratic Polynomial y = x² – 6x + 9 has only one zero i.e., 3.

Question 4.
How will you verify if a quadratic polynomial it has only one zero?  (Page No. 55)
Answer:
If the graph of the given quadratic polynomial touches X – axis at exactly one point, then I can confirm it has only one zero.

Question 5.
Write three quadratic polynomials that have no zeroes for x that are real numbers.  (Page No. 55)
Answer:
The quadratic polynomials y = 2x² – 4x + 5 and y = – 3x² + 2x – 1 and y = x² – 2x + 4 have no zeroes.

Question 6.
Find the zeroes of cubic polynomials
(i) – x³
(ii) x² – x³
(iii) x³ – 5x² + 6x
without drawing the graph of the polynomial.  (Page No. 57)
Answer:
i) Given polynomial is y = – x³
f(x) = -x³ ; f(x) = 0
x³ = 0
x = [latex]\sqrt[3]{0}[/latex] = 0
∴ Zero of the polynomial f(x) is only one i.e., 0.

ii) Given that y = x² – x³
f(x) = x² (1 – x)
f(x) = 0
⇒ x² (1 – x) = 0
⇒ x² = 0 and 1 – x = 0
⇒ x = 0 and x = 1
∴ The zeroes of the polynomial f(x) are two i.e., 0 and 1.

iii) Given that x³ – 5x² + 6x Let f(x) = x³ – 5x² + 6x
= x(x² – 5x + 6)
= x(x² – 2x – 3x + 6)
= x[x(x – 2) – 3(x – 2)]
= x(x – 2) (x – 3)
∴ The zeroes of the polynomial f(x) are x = 0 and x = 2 and x = 3

Do these

Question 1.
Find the zeroes of the quadratic polynomials given below. Find the sum and product of the zeroes and verify relationship to the coefficients of terms in the polynomial. (Page No. 62)
i) p(x) = x² – x – 6
ii) p(x) = x² – 4x + 3
iii) p(x) = x² – 4
iv) p(x) = x² + 2x + 1
Answer:
i) Given polynomial p(x) = x² – x – 6
We have x² – x – 6 = x² – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x – 3) (x + 2)
So, the value of x² – x – 6 is zero when x – 3 = 0 or x + 2 = 0
i.e., x = 3 or x = -2
So, the zeroes of x² – x – 6 are 3 and – 2.
∴ Sum of the zeroes = 3 – 2 = 1
= – [latex]\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-(-1)}{1}[/latex] = 1
And product of the zeroes = 3 × (-2) = -6
= [latex]\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-6}{1}[/latex] = -6

ii) p(x) = x² – 4x + 3
Answer:
Given polynomial p(x) = x² – 4x + 3
We have, x² – 4x + 3 = x² – 3x – x + 3
= x(x – 3) – 1 (x – 3)
= (x – 3) (x – 1)
So, the value of x² – 4x + 3 is zero when x – 3 = 0 or x – 1 =0, i.e.,
when x = 3 or x = 1 So, the zeroes of x² – 4x + 3 are 3 and 1
∴ Sum of the zeroes = 3 + 1 = 4
= – [latex]\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-(-4)}{1}[/latex] = 4
And product of the zeroes = 3 × 1 = 3
= [latex]\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{3}{1}[/latex] = 3

iii) Given polynomial p(x) = x² – 4
We have, x² – 4 = (x – 2) (x + 2)
So, the value of x² – 4 is zero
when x – 2 = 0 or x + 2 = 0
i.e., x = 2 or x = – 2
So the zeroes of x² – 4 are 2 and – 2
∴ Sum of the zeroes = 2 + (- 2) = 0
= – [latex]\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-0}{1}[/latex] = 0
And product of the zeroes = 2 × (-2) = -4
= [latex]\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-4}{1}[/latex] = -4

iv) Given polynomial p(x) = x² + 2x + 1
We have x² + 2x + 1 = x² + x + x + 1
= x(x + 1) + l(x + 1)
= (x + 1) (x + 1)
So, the value of x² + 2x + 1 is zero
when x + 1 = 0 (or) x + 1 = 0, i.e.,
when x = – 1 or – 1
o, the zeroes of x² + 2x + 1 are – 1 and – 1.
∴ Sum of the zeroes = (-1) + (-1) = -2
= – [latex]\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{-2}{1}[/latex] = -2
And product of the zeroes = (-1) × (-1) = 1
= [latex]\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}[/latex] = [latex]\frac{1}{1}[/latex] = 1

Question 2.
If α, β and γ are the zeroes of the given cubic polynomials, find the values as given in the table. (Page No. 66)

Answer:
l) Given polynomial is x³ + 3x² – x – 2.
Comparing given polynomial with ax³ + bx² + cx + d,
the values are a = 1, b = 3, c = -l, d = -2
α + β + γ = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-3}{1}[/latex] = -3
αβ + βγ + γα = [latex]\frac{c}{a}[/latex] = [latex]\frac{-1}{1}[/latex] = -1
αβγ = [latex]\frac{-d}{a}[/latex] = [latex]\frac{-(-2)}{1}[/latex] = 2

2) Given polynomial is 4x³ + 8x² – 6x – 2
Compare the polynomial with ax³ + bx² + cx + d = 0
Then a = 4, b = 8, c = – 6 and d = – 2
α + β + γ = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-8}{4}[/latex] = -2
αβ + βγ + γα = [latex]\frac{c}{a}[/latex] = [latex]\frac{-6}{4}[/latex] = [latex]\frac{-3}{2}[/latex]
αβγ = [latex]\frac{-d}{a}[/latex] = [latex]\frac{-(-2)}{4}[/latex] = [latex]\frac{1}{2}[/latex]

3) Given polynomial is x³ + 4x² – 5x – 2
Compare the polynomial with ax³ + bx² + cx + d = 0
Then a = 1, b = 4, c = – 5 and d = – 2
α + β + γ = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-4}{1}[/latex] = -4
αβ + βγ + γα = [latex]\frac{c}{a}[/latex] = [latex]\frac{-5}{1}[/latex] = -5
αβγ = [latex]\frac{-d}{a}[/latex] = [latex]\frac{-(-2)}{1}[/latex] = 2

4) Given polynomial is x³ + 5x² + 4
Compare the polynomial with ax³ + bx² + cx + d = 0
Then a = 1, b = 5, c = 0 and d = 4
α + β + γ = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-5}{1}[/latex] = -5
αβ + βγ + γα = [latex]\frac{c}{a}[/latex] = [latex]\frac{0}{1}[/latex] = 0
αβγ = [latex]\frac{-d}{a}[/latex] = [latex]\frac{-4}{1}[/latex] = -4

Try this

Question 1.
i) Find a quadratic polynomial with zeroes -2 and [latex]\frac{1}{3}[/latex]. (Page No. 64)
Answer:
Let the quadratic polynomial be ax² + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = – 2 and β = [latex]\frac{1}{3}[/latex]
Sum of the zeroes = α + β
= -2 + [latex]\frac{1}{3}[/latex] = [latex]\frac{-5}{3}[/latex]
Product of the zeroes = αβ
= [latex]\frac{1}{3}[/latex] × (-2) = [latex]\frac{-2}{3}[/latex]
∴ ax² + bx + c is [x² – (α + β)x + αβ]
= [x² – [latex]\left(\frac{-5}{3}\right)[/latex]x + [latex]\left(\frac{-2}{3}\right)[/latex]]
the quadratic polynomial will be 3x² + 5x – 2.

ii) What is the quadratic polynomial whose sum of zeroes is [latex]\frac{-3}{2}[/latex] and the product of zeroes is -1.
Answer:
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Here α + β = [latex]\frac{-3}{2}[/latex] and αβ = -1
Thus, the polynomial formed = x² – (α + β)x + αβ
= x² – [latex]\left(\frac{-3}{2}\right)[/latex]x + (-1)
= x² + [latex]\frac{3x}{2}[/latex] – 1
The other polynomials are (x² + [latex]\frac{3x}{2}[/latex] – 1)
then the polynomial is 2x² + 3x – 2.

AP State Syllabus SSC 10th Class Maths Solutions 2nd Lesson Sets InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 2 Sets InText Questions and Answers.

10th Class Maths 2nd Lesson Sets InText Questions and Answers

Question 1.
List the teeth under each of the following type (Page No. 25)

i) Incisors
Answer:
Central incisors = 4
Lateral incisors = 4
Total incisors = 8
ii) Canines
Answer:
Total canines = 4
iii) Pre-molars
Answer:
First premolars = 4
Second premolars = 4
Total premolars = 8
iv) Molars
Answer:
First molars = 4
Second molars = 4
Third molars = 4
Total molars = 12

Question 2.
Identify and write the “common property” of the following collections. (Page No. 26)
1) 2, 4, 6, 8, …….
Answer:
All are even numbers {x : x is even}
2) 2, 3, 5, 7, 11, …….
Answer:
All are prime numbers (x : x is a prime}
3) 1, 4, 9, 16, …….
Answer:
All are perfect squares
(x : x is a perfect square}
4) January, February, March, April,…
Answer:
All are English months
{x : x is a month of the year}
5) Thumb, index finger, middle finger, ring finger, pinky.
Answer:
All are fingers of a hand
{x : x is a finger of a hand}

Question 3.
Write the following sets. (Page No. 27)
1) Set of the first five positive integers.
Answer:
{11, 2, 3, 4, 5}
2) Set of multiples of 5 which are more than 100 and less than 125.
Answer:
{105, 110, 115, 120}
3) Set of first five cubic numbers.
Answer:
{1³, 2³, 3³, 4³, 5³}
{1, 8, 27, 64, 125}
4) Set of digits in the Ramanujan number.
Answer:
Ramanujan’s number is 1729
{1, 2, 7, 9}

Question 4.
Some numbers are given below. Decide the numbers to which number sets they belong to and does not belong to and express with correct symbols. (Page No. 28)
i) 1
Answer:
1 ∈ N
ii) 0
Answer:
0 ∈ W and 0 ∉ N
iii) -4
Answer:
– 4 ∈ I and – 4 ∉ N
iv) [latex]\frac{5}{6}[/latex]
Answer:
[latex]\frac{5}{6}[/latex] ∈ Q and [latex]\frac{5}{6}[/latex] ∉ Z
v) [latex]1 . \overline{3}[/latex]
Answer:
[latex]1 . \overline{3}[/latex] ∉ N and [latex]1 . \overline{3}[/latex] ∉ Z
vi) √2
Answer:
√2 ∈ S and √2 ∉ Q
vii) log 2
Answer:
log 2 ∉ N
viii) 0.03
Answer:
0.03 ∉ Q
ix) π
Answer:
π ∉ Z
x) [latex]\sqrt{-4}[/latex]
Answer:
[latex]\sqrt{-4}[/latex] ∉ Q and [latex]\sqrt{-4}[/latex] ∈ C

Question 5.
List the elements of the following sets. (Page No. 29)
i) G = {all the factors of 20}
ii) F = {the multiples of 4 between 17 and 61 which are divisible by 7}
iii) S = {x : x is a letter in the word ‘MADAM’}
iv) P = {x : x is a whole number between 3.5 and 6.7}
Answer:
i) G = {1, 2, 4, 5, 10, 20}
ii) Multiples of 4 between 17 and 61
x = {20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60}
F = {28, 56}
iii) S = {M, D, A}
iv) P = {4, 5, 6}

Question 6.
Write the following sets in the roster form.   (Page No. 29)
i) B is the set of all months in a year having 30 days.
ii) P is the set of all prime numbers smaller than 10.
iii) X is the set of the colours of the rainbow.
Answer:
i) B = {April, June, September, November}
ii) P = {2, 3, 5, 7}
iii) X = {Violet, Indigo, Blue, Green, Yellow, Orange, Red}

Question 7.
A is the set of factors of 12. Which one of the following is not a member of A?   (Page No. 29)
A) 1
B) 4
C) 5
D) 12
Answer:
[C]

Think & Discuss

Question 1.
Observe the following collections and prepare as many as generalized statements you can describing their more properties. (Page No. 26)
i) 2, 4, 6, 8,….
Answer:
a) All even natural numbers
b) All positive even integers
c) Multiples of 2

ii) 1, 4, 9, 16, …..
Answer:
a) Squares of natural numbers
b) All perfect square numbers

Question 2.
Can you write set of rational numbers listing elements in it? (Page No. 28)
Answer:
We can’t list all elements in the set of rational numbers. We know that rational numbers are infinite.

Try this

Question 1.
Write some sets of your choice, involving algebraic and geometrical ideas. (Page No. 29)
Answer:
The set of all natural numbers ‘x’ such that 4x + 9 < 50,
ii) A = {x : x is an integer and -3 ≤ x ≤ 7}
iii) B = {Equilateral triangle, Right angled triangle, Scalene triangle, Obtuse angled triangle, Acute angled triangle)
iv) C = {Rectangle, Square, Parallelogram, Rhombus, Trapezium}

Question 2.
Match roster forms with the set builder form. (Page No. 29)

Answer:
i) d
ii) c
iii) a
iv) b

Do this

Question 1.
A = {1, 2, 3, 4},
B = {2, 4},
C = {1, 2, 3, 4, 7}, ∅ = { }.
Fill in the blanks with ⊂ or ⊄.  (Page No. 33)
i) A …. B
ii) C …. A
iii) B …. A
iv)A …. C
v) B …. C
vi) ∅ …. B
Answer:
i) A ⊄ B
ii) C ⊄ A
iii) B ⊆ A
iv) A ⊆ C
v) B ⊆ C
vi) ∅ ⊆ B

Question 2.
State which of the following statements are true.    (Page No. 33)
i) { } = ∅
ii) ∅ = 0
iii) 0 = { 0 }
Answer:
i) True (T)
ii) False (F)
iii) False (F)

Question 3.
Let A = {1, 3, 7, 8} and B = [2, 4, 7, 9}.
Find A ∩ B.     (Page No. 37)
Answer:
Given sets A = (1, 3, 7, 8} and B = {2,4, 7,9}
A ∩ B = {1, 3, 7, 8} ∩ (2, 4, 7, 9} = {7}

Question 4.
If A = {6,9,11 }; ∅ = {}, find A ∪ ∅, A ∩ ∅).  (Page No. 37)
Answer:
Given sets
A = {6, 9, 11} and ∅ = { }
A ∪ ∅ = {6, 9, 11} ∪ { }
= {6, 9, 11} = A
∴ A ∪ ∅ = A
A ∩ ∅ = {6,9,11} ∩ { } = { } = ∅
∴ A ∩ ∅ = ∅

Question 5.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
B = {2, 3, 5, 7}. Find A ∩ B and show that A ∩ B = B.    (Page No. 37)
Answer:
Given sets
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {2, 3, 5, 7}
A ∩ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {2, 3, 5, 7}
= {2, 3, 5, 7} = B
∴ A ∩ B = B

Question 6.
If A = {4, 5, 6}; B = {7, 8}, then show that A ∪ B = B ∪ A.  (Page No. 37)
Answer:
Given sets are
A = {4, 5, 6} and B = {7, 8}
A ∪ B = {4, 5, 6} ∪ {7, 8}
= {4, 5, 6, 7, 8}.
B ∪ A = {7, 8} ∪ {4, 5, 6}
= {4, 5, 6, 7, 8}
∴ A ∪ B = B ∪ A.

Question 7.
If A = {1, 2, 3, 4, 5 }; B = {4, 5, 6, 7}, then find A – B and B – A. Are they equal?  (Page No. 38)
Answer:
Given sets are
A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7}
A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7}
= {1, 2, 3}
B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5}
= {6, 7}
∴ No, A – B ≠ B – A.

Question 8.
If V = {a, e, i, o, u} and B = {a, i, k, u}, find V – B and B – V.    (Page No. 38)
Answer:
Given sets are
V = {a, e, i, o, u} and B = {a, i, k, u}
V – B = {a, e, i, o, u} – {a, i, k, u}
= {e, o}
B – V = {a, i, k, u} – {a, e, i, o, u}
= {k}.

Try this

Question 1.
A = {set of quadrilaterals},
B = {square, rectangle, trapezium, rhombus}.
State whether A ⊂ B or B ⊂ A. Justify your answer.     (Page No. 33)
Answer:
A = {set of quadrilaterals} means A = {square, rectangle/trapezium, rhombus, parallelogram}
B = {square, rectangle, trapezium, rhombus}
So, B ⊂ A because A’ is having elements more than ‘B’.

Question 2.
If A = {a, b, c, d}. How many subsets does the set A have?    (Page No. 33)
A) 5 B) 6 C) 16 D) 65
Answer:
Given A = {a, b, c, d}
n(A) = 4
Number of subsets for a set, which is having ‘n’ elements is 2ⁿ.
So n(A) = 4
Number of subsets for A is 2⁴ = 16.
Answer is [C].

Question 3.
P is the set of factors of 5, Q is the set of factors of 25 and R is the set of factors of 125. Which one of the following is false?    (Page No. 33)
A) P ⊂ Q
B) Q ⊂ R
C) R ⊂ P
D) P ⊂ R
Answer: [C]

Question 4.
A is the set of prime numbers smaller than 10, B is the set of odd numbers < 10 and C is the set of even numbers < 10. How many of the following statements are true?    (Page No. 33)
i) A ⊂ B
ii) B ⊂ A
iii) A ⊂ C
iv) C ⊂ A
v) B ⊂ C
vi) C ⊂ B
Answer:
All the statements are false.

Question 5.
List out some sets A and B and choose their elements such that A and B are disjoint.  (Page No. 37)
Answer:
Consider the disjoint sets
A = {1, 2, 3, 4} and B = {a, b, c}

Question 6.
If A = {2, 3, 5}, find A ∪ ∅ and ∅ ∪ A and compare.    (Page No. 37)
Answer:
Given sets A = {2, 3, 5} and ∅ = { }
A ∪ ∅ = {2,3,5} ∪ { } = {2,3,5}
∅ ∪ A = { } ∪ {2, 3, 5} = {2,3,5}
A ∪ v = ∅ ∪ A = A

Question 7.
If A = {1, 2, 3, 4}; B = {1, 2, 3, 4, 5, 6, 7, 8}, then find A ∪ B, A ∩ B. What do you notice about the result?   (Page No. 37)
Answer:
Given sets are
A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8}
A ∪ B = {1, 2, 3, 4} ∪ {1, 2, 3, 4, 5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8} = B
A ∩ B = {1, 2, 3, 4} ∩ {1, 2, 3, 4, 5, 6, 7, 8} = {1, 2, 3, 4} = A
If A ⊂ B, then A ∪ B = B and A ∩ B = A

Question 8.
A = {1, 2, 3, 4, 5, 6}; B = {2, 4, 6, 8, 10}. Find the intersection of A and B.     (Page No. 37)
Answer:
Given sets are
A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8, 10}
A ∩ B = {1, 2, 3, 4, 5, 6} ∩ {2, 4, 6, 8, 10} = {2, 4, 6}

Think & Discuss

Question 1.
Is empty set subset to every set?    (Page No. 34)
Answer:
‘Yes’. Empty set is subset to every set
Justify: If A ⊂ B, it means all the elements of set ‘A’ belong to set ‘B’.
In other words we can say no element of ‘A’ missed in set B.
now empty set means which has no elements, now no element of empty set can be missed in any set. So we can write empty set is subset of every set.

Question 2.
Is any set subset to itself?    (Page No. 34)
Answer:
‘Yes’. Every set is subset to itself.
Let ‘A’ is any set.
Now every element of ‘A’ definitely belongs to ‘A’.
So A ⊂ A
Hence every set is a subset to it.

Question 3.
You are given two sets such that a set is not a subset of the other. If you have to prove this, how do you prove?    (Page No. 34)
Answer:
Let the given sets are ‘A’ and ‘B’.
To prove are set (A) is not subset of other (B).
We check if all elements of ‘A’ belong to the set ‘B’ or not.
If any of the element doesn’t belong to ‘B’ then we can say ‘A’ is not subset of ‘B’. So we have to prove at least one element of ‘A’ does not belong to ‘B’.
Hence ‘A’ is not subset of ‘B’.

Question 4.
The intersection of any two disjoint sets is a null set. Justify your answer.    (Page No. 37)
Answer:
Let A and B be any two disjoint sets,
i.e., A and B have no elements in common.
∴ A ∩ B is a null set. (∵ A ∩ B is the set of all elements which are common to both A and B)

Question 5.
The sets A – B, B – A and A ∩ B are mutually disjoint sets. Use examples to observe if this is true.    (Page No. 38)
Answer:
Let the sets are A = {1, 2, 3, 4} and B = {5, 6, 7, 8}
A – B = {1, 2, 3, 4} – {5, 6, 7, 8} = {1, 2, 3, 4}
B – A = {5, 6, 7, 8} – {1, 2, 3, 4} = {5, 6, 7, 8}
A ∩ B = {1, 2, 3, 4} ∩ {5, 6, 7, 8} = { } = ∅
∴ A – B, B – A and A ∩ B are disjoint sets.

Do these

Question 1.
Which of the following are empty sets? Justify your answer.    (Page No. 44)
i) Set of integers which lie between 2 and 3 .
ii) Set of natural numbers that are smaller than 1.
iii) Set of odd numbers that leave remainder zero, when divided by 2.
Answer:
i) This is null set. We know that there is no integer that lie between 2 and 3.
ii) This is also a null set. We know that there is’ no natural number less than ‘1’.
iii) This is a null set. We know that odd numbers do not leave remainder zero when divided by 2.

Question 2.
State which of the following sets are finite and which are infinite. Give reasons for your answer.    (Page No. 44)
i) A = {x : x e N and x < 100}
ii) B = {x : x e N and x ≤ 5}
iii) C = {1² , 2², 3², ……}
iv) D = {1, 2, 3, 4}
v) {x : x is a day of the week}
Answer:
i) A = (1, 2, 3, 4, , 98, 99}
This set is finite, because there are 99 numbers possible to count.
ii) B = {1, 2, 3,  4, 5}
This set is finite because there are 5 numbers possible to count.
iii) C = {1² , 2², 3², ……}
This set is infinite because there are infinite numbers.
iv) D – {1, 2, 3, 4}
This set is finite because there are 4 numbers that are possible to count.
v) E = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
This set is finite, because there are 7 days in a week possible to count.

Question 3.
Tick the set which is infinite.      (Page No. 44)
A) The set of whole numbers < 10
B) The set of prime numbers < 10
C) The set of integers < 10
D) The set of factors of 10
Answer:
[C]
The set of integers < 10
{….., -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Try this

Question 1.
Which of the following sets are empty sets? Justify your answer.    (Page No. 44)
i) A = {x : x² = 4 and 3x = 9}.
ii) The set of all triangles in a plane having the sum of their three angles less than 180.
Answer:
i) x² = 4 ⇒ x = ± 2
3x = 9 ⇒ x = 3
The value of ‘x’ is not same in both cases, so this is a null set.
ii) This is a null set, because the sum of the three angles of a triangle is equal to 180°.

Question 2.
B = {x : x + 5 = 5} is not an empty set. Why?   (Page No. 44)
Answer:
B = {x: x + 5 = 5} is not an empty set
let x ∈ Z or x ∈ W
then for x = 0 ⇒ x + 5 = 0 + 5 = 5
So if x ∈ W, or x ∈ Z then for x = 0,
x + 5 = 5 is true.
Then the set B = {0} which is not an empty set.
Note: But if x ∈ N
We will have no ‘x’ such that x + 5 = 5
then ‘B’ will be an empty set.
But in the textbook it is not given whether x ∈ N (or) x ∈ W (or) x ∈ Z.
Hence we consider first one.

Think & Discuss

Question 1.
An empty set is a finite set. Is this statement true or false? Why?   (Page No. 44)
Answer:
Yes, it is a finite set because there is finite number i.e., ‘0’ elements it consists.

Think & Discuss

Question 1.
What is the relation between n(A), n(B), n(A ∩ B) and n(A ∪ B)?   (Page No. 45)
Answer:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B). This is called Fundamental theorem of sets.

Question 2.
If A and B are disjoint sets, then how can you find n(A ∪ B)?    (Page No. 45)
Answer:
If A and B are disjoint then A ∩ B is a null set.
∴ n(A ∩ B) = 0 and it gives us n(A ∪ B) = n (A) + n(B).

AP State Board Syllabus AP SSC 10th Class Hindi Textbook Solutions Chapter 1 बरसते बदल Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Hindi Solutions Chapter 1 बरसते बदल

10th Class Hindi Chapter 1 बरसते बदल Textbook Questions and Answers

InText Questions (Textbook Page No. 1)

प्रश्न 1.
मीटे गीत कौन गाती है?
उत्तर:
मीठे गीत कोयल गाती है।

प्रश्न 2.
प्यासी धरती पानी किससे माँगती है?
उत्तर:
प्यासी धरती पानी मेघों से माँगती है।

प्रश्न 3.
बादल प्रकृति की शोभा बढ़ाते हैं। कैसे?
उत्तर:
नीले गगन में काले-काले बादल छाये रहते हैं। ये बरसकर हमें पानी देते हैं। धरती पर स्थित सारी प्रकृति को जीवन दान मिलता है। हर जगह हरियाली छा जाती है। सब पानी के स्रोत भरकर सुंदर लगते हैं। प्राणिमात्र के जीवन में हर्ष उमड पडता है। सारा वातावरण खुशहाल हो शोभायमान लगता है। इस तरह बादल प्रकृति की शोभा बढाते हैं।

InText Questions (Textbook Page No. 2)

प्रश्न 1.
मेघ, बिजली और बूंदों का वर्णन यहाँ कैसे किया गया है?
उत्तर:
‘बरसते बादल’ कविता में कविवर पंतजी ने सावन के समय की प्राकृतिक चीजों का वर्णन किया है। वर्षा के समय घने काले मेघ आसमान में छाये झम – झम बरसते हैं। काले मेघों के बीच बिजली चम – चम चमकती है। वर्षा की बूंदें पेडों से छनकर छम – छम गिरती हैं।

प्रश्न 2.
प्रकृति की कौन – कौनसी चीजें मन को छू लेती हैं?
उत्तर:
सावन के समय की प्रकृति मनमोहक होती है। घुमडते बरसनेवाले घन घोर बादल, वर्षा की बूंदें, चमकनेवाली बिजली, बूंदों के रिमझिम स्वर, बहती जल धाराएँ, पेड़ – पौधे, आदि प्रकृति की चीजें मन को छू लेती हैं।

प्रश्न 3.
तृण – तृण की प्रसन्नता का क्या भाव है?
उत्तर:
धरती पर वर्षा के होने से पानी की धाराएँ बहती हैं। इससे रज के कण – कण से कोमल अंकुर फूट पडते हैं। वे खुशी से पुलकित हो झूमते हैं। धरती पर हरियाली छा जाती है। संसार के चारों ओर आनंद और उल्लास होता है। तृण – तृण की प्रसन्नता का यही भाव है।

अर्थग्राह्यता-प्रतिक्रिया

अ) प्रश्नों के उत्तर दीजिए।

प्रश्न 1.
धरती की शोभा का प्रमुख कारण वर्षा है। इस पर अपने विचार बताइए।
उत्तर:
सावन के महीने में वर्षा होती है। वर्षा से पानी मिलता है। धरती पर स्थित प्राणिमात्र को जीवन दान मिलता है। सारी प्रकृति में सब ओर हरियाली फैलती है। मिट्टी के कण – कण से कोमल अंकुर फूटते हैं। खेतों में नदी, नाले भर जाते हैं | फसलें उगती हैं। सब प्राणी खुशी से विभिन्न स्वरों में अपना आनंद प्रकट करते हैं । इस तरह कह सकते हैं कि धरती की शोभा का प्रमुख कारण वर्षा ही है।

प्रश्न 2.
घने बादलों का वर्णन अपने शब्दों में कीजिए।
उत्तर:
घने काले बादल सावन के महीने में आसमान में छाये रहते हैं। विविध आकारों में विश्रृंखलता से मंडराते हैं। भीषण ध्वनि करते वे भयानक होते हैं। उनके बीच बिजली चमक उठती है। इनकी शोभा देखनेलायक होती है। ठंडी बहार के छूते ही वे मूसलधार वर्षा देते हैं। प्रकृति में नूतन शोभा नज़र आती है। जन जीवन को आनंदमय बनाते हैं।

आ) वाक्य उचित क्रम में लिखिए।

प्रश्न 1.
हैं झम – झम बरसते झम – झम मेघ के सावन।
उत्तर:
झम – झम – झम – झम मेघ बरसते हैं सावन के।

प्रश्न 2.
गगन में गर्जन घुमड़ – घुमड़ गिर भरते मेघा
उत्तर:
घुमड – घुमड गिर मेघ गगन में भरते गर्जन।

प्रश्न 3.
धरती पर झरती धाराएँ पर धाराओं।
उत्तर:
धाराओं पर धाराएँ झरती धरती पर।

इ) नीचे दिये गये भाव की पंक्तियाँ लिखिए।

प्रश्न 1.
बादलों के घोर अंधकार के बीच बिजली चमक रही है और मन दिन में ही सपने देखने लगा है। .
उत्तर:
चम – चम बिजली चमक रही रे उर में घन के, थम – थम दिन के तम में सपने जगते मन के।

प्रश्न 2.
मिट्टी के कण – कण से कोमल अंकुर फूट रहे हैं।
उत्तर:
रज के कण – कण में तृण – तृण को पुलकावलि थर।।

प्रश्न 3.
कवि चाहता है कि जीवन में सावन बार – बार आयें और सब मिलकर झूलों में झूलें।
उत्तर:
आओ रे सब मुझे घेर कर गाओ सावन। इंद्रधनुष के झूले में झूलें मिल सब जन।।

ई) पद्यांश पढ़कर प्रश्नों के उत्तर दीजिए।

बादल और बूंदें, बंद किये हैं बादल ने
अंबर के दरवाज़े सारे, नहीं नज़र आता है सूरज ना कहीं चाँद – सितारे ?
ऐसा मौसम देखकर, चिड़ियों ने भी पंख पसारे,
हो प्रसन्न धरती के वासी, नभ की ओर निहारे॥

1. इसने अंबर के दरवाज़े बंद कर दिये हैं –
अ) आकाश
आ) सूरज
इ) चाँद
ई) बादल
उत्तर:
ई) बादल

2. पंख किसने पसारे हैं?
अ) चिड़िया
आ) मौसम
इ) धरती
ई) सितारे
उत्तर:
अ) चिड़िया

3. पद्यांश में आया युग्म शब्द है –
अ) बादल – अंबर
आ) सूरज – चाँद
इ) चाँद – सितारे
ई) धरती – वासी
उत्तर:
इ) चाँद – सितारे

4. धरती के लोग किस ओर निहार रहे हैं?
अ) चिड़िया
आ) नभ
इ) बादल
ई) चाँद
उत्तर:
आ) नभ

5. इस कविता का विषय है –
अ) प्रकृति
आ) सूरज
इ) तारे
ई) अंबर
उत्तर:
अ) प्रकृति

अभिव्यक्ति – सृजनात्मकता

अ) इन प्रश्नों के उत्तर तीन – चार पंक्तियों में लिखिए।

प्रश्न 1.
वर्षा सभी प्राणियों के लिए जीवन का आधार है। कैसे?
उत्तर:
वर्षा सभी प्राणियों के लिए आवश्यक है। वर्षा से ही संसार का चक्र चलता है। बादल वर्षा के रूप में बरसकर पानी देते हैं। धरती के सब भूभागों में पानी जमा रहता है। यह पानी पेय जल, खाना, दाना, बिजली आदि अनेक आवश्यकताओं की पूर्ति करता है। प्रकृति में हरियाली इसीसे व्याप्त होती है । वर्षा के बिना धरती पर प्राणिमात्र का जीवन यापन असंभव है। अतः कह सकते हैं कि वर्षा सभी प्राणियों के जीवन का आधार है।

प्रश्न 2.
वर्षा ऋतु के प्राकृतिक सौंदर्य पर अपने विचार लिखिए।
उत्तर:
वर्षा ऋतु सदा से सबकी प्रिय ऋतु रही है। आसमान में फैले काले, घनघोर बादल बरसते हैं। बिजली की चकाचौंध चमक होती है। वर्षा की बूंदें रिमझिम बरसती हैं। पानी की धाराओं से धरती पुलकित होती है। मिट्टी के कण – कण से कोमल अंकुर फूट पड़ते हैं। पेड – पौधे हरियाली से झूमते हैं। पशु – पक्षी, मानव और हर प्राणी आनंद विभोर हो जाते हैं। विभिन्न जीवों के आनंद स्वरों से सारी प्रकृति मनमोहक होती है।

आ) ‘बरसते बादल’ कविता में प्रकृति का सुंदर चित्रण है। उसे अपने शब्दों में लिखिए।
(या)
‘बरसते बादल कविता के आधार पर प्रकृति का वर्णन कीजिए।
(या)
‘बरसते बादल कविता का सारांश अपने शब्दों में लिखिए।
(या)
पंतजी ने वर्षा ऋतु के प्राकृतिक सौंदर्य का संदर चित्रण किया है। अपने शब्दों में लिखिए।
(या)
‘बरसते बादल’ कविता का वर्णन अपने शब्दों में कीजिए।
उत्तर:
कवि का नाम : श्री सुमित्रानंदन पंत
जीवनकाल : 1900 – 1977
रचनाएँ : वीणा, ग्रंथि, पल्लव आदि।
पुरस्कार : ज्ञानपीठ (विवंबरा) साहित्य आकादमी, सोवियत रूस।
सारांश : आधुनिक हिंदी के विख्यात कवि हैं श्री सुमित्रानंदन पंतजी। प्रकृति सौंदर्य के वर्णन में आप सुकुमार और बेजोड कवि माने जाते हैं। वीणा, ग्रंथि, पल्लव, ग्राम्या, युगांत आदि आपके प्रसिद्ध काव्य संकलन हैं। “चिदंबरा” काव्य रचना के लिए आपको ज्ञानपीठ पुरस्कार मिला।

“बरसते बादल” कविता में पंतजी ने वर्षा ऋतु का सुंदर और सजीव चित्रण किया है।

पंतजी कहते हैं कि वर्षा ऋतु हमेशा से सबकी प्रिय ऋतु रही है। उसमें भी सावन का महीना अधिक सुंदर और मनभावन होता है। सावन की वर्षा सबका मन मोहती है।

सावन के मेघ झम – झम बरसते हैं। वर्षा की बूंदें पेडों से छनकर छम – छम आवाज़ करती धरती पर गिरती हैं। मेघों के हृदय में बिजली चम – चम चमकती है। दिन में भी वर्षा के कारण अंधेरा छा जाता है। लोगों के दिलों में सपने जगने लगते हैं।

वर्षा के बरसने पर दादुर टर – टर आवाज़ करते हैं। झींगुर झींझी आवाज़ देते हैं। मोर म्यव – म्यव करते नाचते हैं। पपीहे पीउ – पीउ करके कूकते हैं। सोनबालक पक्षी गीली – खुशी से आह्वान करते हैं। आसमान पर बादल घुमडते गरजते हैं। ..

रिमझिम बरसनेयाली बूंदों के स्वर हम से कुछ कहते हैं। अर्थात् मन खुश करते हैं। उनके छूते ही शरीर के रोम सिहर उठते हैं। धरती पर जल की धाराएँ झरती हैं। इससे मिट्टी के कण – कण में कोमल अंकुर फूट पडते हैं। अर्थात् मिट्टी का हर कण अतिप्रसन्न लगता है।

वर्षा की धाराओं के साथ कवि का मन झूलने लगता है। वे लोगों को आमंत्रित करते हैं कि आप सब आइए मुझे घेरकर सावन के गीत गाइए। हम सब लोग इंद्रधनुष के झूले में झूलने का आनंद लें। यह कामना करें कि मनभावन सावन हमारे जीवन में बार – बार आये।

विशेषता : इस कविता में प्रकृति का सुंदर चित्रण अंकित किया है। इस कविता से संवेदनशीलता का विकास होता है।

इ) प्रकृति सौंदर्य पर एक छोटी-सी कविता लिखिए।
उत्तर:
ये नदियों की कल कल
ये मौसम की हलचल
ये पर्वत की चोटियाँ
ये झींगुर की सीटियाँ
कुछ कहना चाहती हैं हम से
ये प्रकृति शायद कुछ कहना चाहती है हम से ।।

ई) ‘फिर – फिर आये जीवन में सावन मनभावन’ ऐसा क्यों कहा गया होगा? स्पष्ट कीजिए।
उत्तर:
वर्षा ऋतु सबकी प्रिय ऋतु है। यह ऋतुओं की रानी कहलाती है। सावन के आने से प्रकृति रमणीय होती है। प्रकृति का कण – कण अति प्रसन्न दिखता है। पशु – पक्षी, पेड – पौधे मानव यहाँ तक कि धरती के सभी प्राणी, धरती तक खुशी से नाच उठते हैं। प्रत्येक जीवन खुशी से गीत गाने लगता है। सावन के समय बरसनेवाली वर्षा का पानी सबके जीवन का आधार है। प्राणिमात्र के जीवन यापन के लिए आवश्यक और महत्वपूर्ण है। इसीलिए कविवर पंतजी ने मनभावन सावन को बार – बार आने के लिए कहा होगा।

भाषा की बात

अ) कोष्ठक में दी गयी सूचना पढ़िए और उसके अनुसार कीजिए।

1. तरु, गगन, घन (प्रत्येक शब्द का वाक्य प्रयोग करते हुए पर्याय शब्द लिखिए।)
उत्तर:
वाक्य प्रयोग
तरुः – हमें तरु फूल और फल देते हैं।
गगन – हवाई जहाज़ गगन में उड़ रहा है।
घनः – आसमान में काले घन छाये हुये हैं।

पर्याय शब्द
तरु – पेड, पादप, वृक्ष
गगन – आकाश, आसमान, नभ
घन – बादल, मेघ

2. साक्न, सपना, सूरज (एक-एक शब्द का तत्सम रूप लिखिए।)
उत्तर:
तत्सम रूप
सावन – श्रावण सपना – स्वप्न
सूरज – सूर्य

3. गण, वारि, चंद्र (एक-एक शब्द का तद्भव रूप लिखिए।)
उत्तर:
तदभव रूप
गण – गन
वारि – बारि
चंद्र – चाँद

4. चम – चम, तृण – तृण, फिर – फिर (पुनरुक्ति शब्दों से वाक्य प्रयोग कीजिए।)
उत्तर:
चम – चम = बिजली चम – चम चमक रही है।
तृण – तृण = तृण – तृण पुलकित हो रहा है।
फिर – फिर = सावन फिर – फिर आता तो कितना अच्छा होगा।

आ) इन्हें समझिए और सूचना के अनुसार कीजिए।

1. धाराओं पर धाराएँ झरती धरती पर। (अंतर स्पष्ट कीजिए।)
उत्तर:
यहाँ पंत जी ने “धारा” शब्द को दो. बार प्रयोग किया हैं। यह संज्ञा शब्द है। इसका बहुवचन रूप ‘धाराएँ’ है। इसके साथ “पर” कारक जोडने से “धाराएँ” शब्द रूपांतरित होकर “धाराओं” बन गया है। इस प्रकार के वर्णन से वाक्य का सौंदर्य बढ़ता है।

(अंतर स्पष्ट कीजिए।)
“झूले” शब्द का मूल रूप झूला है। यह संज्ञा शब्द है। इसके साथ में “में” कारक के जोडने से झूले में रूपांतरित हो गया है। “झूलें” शब्द तो ‘झूलना’ क्रिया का रूपांतरण है।

(रेखांकित शब्द का पद परिचय दीजिए।)
संज्ञा, जातिवाचक संज्ञा, पुंलिंग, बहुवचन, कर्ता कारक।
एक शब्द में लिखिए।)

मनभावन
(समास पहचानिए।)
द्वंद्व समास
द्वंद्व समास
खेलते – कूदते बच्चे तंदुरुस्त रहते हैं।
बहते पानी में गंदगी नहीं रहती है।
उडती पंछी वर्षा में भीग गयी है।
रोती बच्ची माँ की गोद पहुंची।
हँसते और खिलते फूलों से उद्यान भरा है।

झम-झम-झम-झम मेघ बरसते हैं सावन के,
छम-छम-छम गिरती बूंदें तरुओं से छन के।

अलंकार शब्द का अर्थ है – आभूषण। किसी बात को साधारण ढंग से न कहकर चमत्कार व सौंदर्यपूर्ण ढंग से कहना ही अलंकार है।

इस कविता में अनुप्रास अलंकार का सुंदर प्रयोग हुआ है। जब वाक्य में कोई अक्षर या शब्द बार – बार प्रयोग होता है तो वहाँ वाक्य का ध्वन्यात्मक सौंदर्य बढ़ जाता है। इस प्रकार का काव्य – सौंदर्य अनुप्रास अलंकार कहलाता है।

परियोजना कार्य

वर्षा, बादल, नदी, सागर, सूरज, चाँद, झरने आदि में किसी एक विषय पर प्रकृति वर्णन से जुड़ी कविता का संग्रह कीजिए। कक्षा में उसका प्रदर्शन कीजिए।

चाँद

चम – चम – चम – चम चंदा चमके
तारे चमके झिलमिल।
आओ – आओ खेले हिल मिल
आज – चाँदनी में हम – सब ।।
ठंडी – ठंडी हवा बह रही
लोरी – सी कुछ गाती।
अभी नहीं सोयेगा कोई
नींद किसे है आती ।।
देखो धीमे – धीमे झूमीं
फूलों के ये पाँखें।

जुही, चमेली चमकी जैसे
बगिया की सौ आँखें।।
खूब भरी है नदी दूध हो
दूध भरा है झरना।
अच्छा लगता आज सभी को
दूर – दूर तक फिरना।
अरे चाँद, तुम कौन बताओ
चाँदी की थाली – से।
प्यारे तारे, झरे फूल से
बोलो, किस डाली से ॥

झरना

कल – कल करता झरना बहता
कानों में रस घोल रहा है।
गुनगुनी धूप, रेत की चादर
माता के आंचल में छुपाकर
जैसे बच्चा सो रहा है।
कल – कल करता झरना बहता
कानों में रस घोल रहा है।
कलख करते पंछी गाते,
तोता मैना गीत सुनाते
मेरा भी मन डोल रहा है।
कल – कल करता झरना बहता
कानों में रस घोल रहा है।
नीला अंबर, मीठा पानी,
प्रकृति कहे सुनो कहानी
जग अपने पट खोल रहा है
कल – कल करता झरना बहता।
कानों में रस घोल रहा है।

बरसते बदल Summary in English

Introduction of the lesson:
Rainy season is always endearing to all. It is worth watching that the beauty of a rainy day. The surrounding nature, flora and fauna, human beings, birds and the Mother Earth sway with ecstasy. This beautiful expression is described here.

Shravana clouds are raining. Rain drops are falling on the branches of trees. Flashes of lightnings are occurring from the hearts of clouds. Though it is a daytime with sunshine, it is dark because of cloudy sky and so dreams are awakening in everybody’s hearts.

Frogs are croaking. Crickets are screaming. Peacocks are dancing beautifully. Swallows are staring at the clouds. Water birds are flying happily making cries. The clouds are spreading over the sky making thundering sounds.

Raindrops are telling something. On touching them, we become horrent. It is raining with flows. Every particle in the earth is startling and tender sprouts are coming out of the earth.

My heart is rocking holding the flows of rain. Come ……. encircle me and sing the songs of Shravana. Let’s go up together in the swing of rainbow. Let’s welcome Shravana into our lives which enlivens and enthralls our hearts again and again.

बरसते बदल Summary in Telugu

ఝమ్ – ఝమ్ – ఝమ్ – ఝమ్ శ్రావణ మేఘాలు వర్షిస్తున్నాయి. చెట్ల కొమ్మలపై ఛమ్ – ఛమ్ – ఛమ్ అంటూ వర్షపు చినుకులు (బిందువులు) పడుతున్నాయి. మేఘాల నుండి (మేఘపు హృదయాల) విద్యుత్ మెరుపులు చమ్ – చమ్ మెరుస్తున్నాయి. ఎండ ఉన్న పగలు అయినప్పటికీ మేఘావృతమై యుండుటవలన కలిగిన చీకటిలో అందరి మనస్సుల్లో స్వప్నాలు జాగృతమవుతున్నాయి.

ఈ కప్పలు టర్ టర్మంటు అరుస్తున్నాయి. కీచురాళ్ళు కీచు కీచుమంటూ ధ్వనిస్తున్నాయి. నెమళ్ళు మ్యవ్ – మ్యవ్ మంటూ నృత్యం చేస్తున్నాయి. పీవు, పీవుమంటు చాతక పక్షులు మేఘాల వంక చూస్తున్నాయి. జలపక్షులు ఆర్ధ సుఖంతో ఎగురుతూ ఆక్రందన చేయుచున్నాయి. మేఘాలు గగనతలంలో గర్జన చేస్తూ ఆకాశాన్ని కమ్ముకున్నాయి.

రిమ్- జిమ్ – రిమ్ – జిమ్ అంటూ వర్షపు చినుకులు ఏదో చెబుతున్నాయి. వాటిని తాకితే వెంట్రుకలు నిక్కబొడుచు కుంటున్నాయి. ధారలు ధారలుగా వర్షం భూమిపై కురుస్తోంది. మట్టిలోని అణువణువు పులకరించి పోగా నేల నుండి కోమలమైన మొక్కల మొలకలు చిగురిస్తున్నాయి.

వర్షపు ధారలను పట్టుకొని నా మనస్సు ఊగుతోంది. రండి అందరూ నన్ను చుట్టుముట్టి శ్రావణ గీతాలను ఆలపించండి. ఇంద్రధనుస్సు ఊయల ఊపులలో మనమందరం కలసి ఊగుదాం. మన జీవితంలోకి మళ్ళీ మళ్ళీ మనస్సును ఆహ్లాదపరచే
శ్రావణం రావాలి.

अभिव्यक्ति-सृजनात्मकता

2 Marks Questions and Answers

निम्नलिखित प्रश्नों के उत्तर दो या तीन वाक्यों में लिखिए।

प्रश्न 1.
तृण – तृण की प्रसन्नता का क्या भाव है?
उत्तर:
धरती पर वर्षा के होने से पानी की धाराएँ बहती हैं। इससे रज के कण – कण से कोमल अंकुर फूट पडते हैं। वे खुशी से पुलकित हो झूमते हैं। धरती पर हरियाली छा जाती है। संसार के चारों ओर आनंद और उल्लास होता है। तृण – तृण की प्रसन्नता का यही भाव है।

प्रश्न 2.
धरती की शोभा का प्रमुख कारण वर्षा है। इस पर अपने विचार बताइए।
उत्तर:
सावन के महीने में वर्षा होती है। वर्षा से पानी मिलता है। धरती पर स्थित प्राणिमात्र को जीवन दान मिलता है। सारी प्रकृति में सब ओर हरियाली फैलती है। मिट्टी के कण – कण से कोमल अंकुर फूटते हैं। खेतों में नदी, नाले भर जाते हैं। फसलें उगती हैं। सब प्राणी खुशी से विभिन्न स्वरों में अपना आनंद प्रकट करते हैं । इस तरह कह सकते हैं कि धरती की शोभा का प्रमुख कारण वर्षा ही है।

प्रश्न 3.
वर्षा से प्रकृति की सुंदरता बढ़ती है। कैसे?
उत्तर:
आसमान में काले बादल छा जाते हैं।

• वर्षा की बूंदें तरुओं पर गिरते हैं। वह दृश्य बड़ा रमणीय है।
• बिजली आसमान के हृदय में चम – चम चमकती है। इस तरह वर्षा से प्रकृति की सुंदरता बढ़ती है।

प्रश्न 4.
वर्षा ऋतु सबकी प्रिय ऋतु है। क्यों?
उत्तर:
निम्नलिखित कारणों से वर्षा ऋतु सबकी प्रिय ऋतु है :

• वर्षा के समय आसमान को घने बादल घेर लेते हैं ।
• बादलों के उर में से बिजली चमक उठती है।
• मेघों के टकराने से मेघ गर्जन भी निकलता है ।
• आसमान में इन्द्रधनुष भी निकलता है । थम-थमाते दिन में भी अंधेरा फैल जाता है |

प्रश्न 5.
वर्षा की कमी या अधिकता हम पर कैसा प्रभाव डालती है?
उत्तर:

• सारी प्रकृति पर वर्षा का प्रभाव बहुत अधिक है।
• वर्षा की कमी के कारण खेत, तालाब, नाले, और नदी सब सूख जाते हैं।
• पीने का पानी की भी कमी होता । यदि वर्षा अधिक हो तो बाढ़ निकलते।
• खेत सड जाते | घर – गाँव डूब जाते।

प्रश्न 6.
वर्षा के समय सभी प्राणी पुलकित होते हैं । वर्णन कीजिए।
उत्तर:
वर्षा के समय सभी प्राणी पुलकित होते हैं। इस कविता में कवि ने खासकर कुछ जीवों का वर्णन किया है। बारिश के मौसम में दादुर टर – टर करते हैं। झींगुर झन – झन बजते हैं। मोर म्यव – म्यव करते हैं। चातक पीऊ – पीऊ बोलते हैं। सोन बालक जल पक्षी आर्दता का सुख पाकर क्रंदन करता है।

प्रश्न 7.
वर्षा के समय प्रकृति की सुंदरता बढ़ती है। कैसे ?
उत्तर:
पेड – पौधे हरे – भरे होकर फल – फूलों से लद जाते हैं। हर तरफ़ हरियाली छा जाती है। फुलवारी महकने लगती है। पक्षी भी पेड़ों के पास आकर चहचहाने लगते हैं। खेत फसलों से लहलहाने लगते हैं। नदी – नाले सारे के सारे पानी से भर जाते हैं। मछलियाँ मस्त होकर नृत्य करने लगती हैं। मनुष्यों में दुगुना उत्साह भर जाता है। इस प्रकार वर्षा के समय प्रकृति की सुंदरता बढ़ती हैं।

प्रश्न 8.
बरसते बादलों को देखकर किसान क्यों प्रसन्न होते हैं?
उत्तर:
नीलाकाश में काले – काले बादल छाये रहते हैं। ठंडी हवा लगते ही वे पानी बरसते हैं। बरसते बादलों को देखकर किसान प्रसन्न होते हैं। किसान लोग खेती बाडी करके आवश्यक खाद्य पदार्थ पैदा करते हैं। खेती बाडी के लिए वर्षा की आवश्यकता है। वर्षा के होते ही किसान खेत जोत कर फसल उगाते लगते हैं। सिंचाई के लिए भी पानी चाहिए। बीज बोने से लेकर फसल उगने तक पानी की आवश्यकता है। इसलिए ऐसा महत्वपूर्ण पानी बरसनेवाले मेघों को देखकर किसान बहुत प्रसन्न होते हैं।

प्रश्न 9.
आपकी प्रिय ऋतु क्या है ? क्यों?
उत्तर:

• मेरी प्रिय ऋतु वर्षा ऋतु है । वर्षा ऋतु हमेशा से सबकी प्रिय ऋतु है ।
• वर्षा के समय प्रकृति की सुंदरता देखने लायक होती है |
• पेड़ – पौधे, पशु-पक्षी, मनुष्य और यहाँ तक कि धरती भी इस ऋतु में खुशी से झूम उठती है ।
• आसमान में निकले इंद्रधनुष, काले – काले बादल, बादलों से उत्पन्न होनेवाली बिजली आदि इस ऋतु में प्रकृति की शोभा बढाते हैं । इस ऋतु में सर्वत्र हरियाली मन मोह लेती है ।

अभिव्यक्ति-सृजनात्मकता

4 Marks Questions and Answers

निम्नलिखित प्रश्नों के उत्तर छह पंक्तियों में लिखिए।

प्रश्न 1.
सुमित्रानदनं पंत के बारे में आप क्या जानते हैं?
(या)
पंत जी प्रकृति के बेजोड कवि हैं। उनके बारे में आप क्या जानते हैं?
(या)
प्रकृति वर्णन में बेजोड कवि सुमित्रानंदन पंतजी का परिचय दीजिए।
(या)
कवि “सुमित्रानंदन पंत” के बारे में आप क्या जानते हैं?
(या)
उत्तर:

• प्रकृति के बेजोड कवि माने जाने वाले सुमित्रानंदन पंत का जन्म सन् 1900 में अल्मोडा में हुआ।
• साहित्य लेखन के लिए इन्हें ‘साहित्य अकादमी’, ‘सोवियत रूस’ और ‘ज्ञानपीठ पुरस्कार’ दिया गया।
• इनकी प्रमुख रचनाएँ हैं – वीणा, ग्रंथि, पल्लव, गुंजन, युगांत, ग्राम्या, स्वर्णकिरण, कला और बूढ़ा चाँद तथा चिदंबरा आदि।
• इन्हें चिदंबरा काव्य संकलन पर ज्ञानपीठ पुरस्कार से सम्मानित किया गया।
• इनका निधन सन् 1977 में हुआ।

प्रश्न 2.
वर्षा ऋतु के प्राकृतिक सौंदर्य पर अपने विचार लिखिए।
उत्तर:
वर्षा ऋतु में प्रकृति बहुत सुंदर लगती है। चारों ओर हरियाली ही हरियाली रहती है। वर्षा की पहली बूंद जब धरती को चूमती है, तब उसका सुंगध वर्णनातीत होता है। वर्षा में खेलकर बच्चे पुलकित होते हैं। कलियाँ खिलती हैं।

वर्षा के कारण हर गली में नदियाँ बहती हैं। उन नदियों में बच्चे कागज़ की नावें छोडते हैं। वर्षा के कारण जन-जन का मन उल्लास से भर जाता है। पेडों पर नये-नये पत्ते आते हैं और नया – नया सुंगध फैलाते हैं। वर्षा ऋतु हमेशा सबकी प्रिय ऋतु रही है। वर्षा के समय प्रकृति की सुंदरता देखने लायक होती है।

प्रश्न 3.
सुमित्रानंदन पंतजी को प्रकृति सौंदर्य चित्रण का बेजोड़ कवि कहा गया है। “बरसते बादल” कविता के आधार पर इस कथन की पुष्टि कीजिए।
उत्तर:
पंतजी ने “बरसते बादल” कविता में सुंदर, मधुर शब्दों का प्रयोग किया है। जिस प्रकार आभूषण नारी की सुंदरता को बढ़ा देते हैं। उसी प्रकार पंतजी ने शब्द रूपी आभूषणों से कविता को सजाकर प्रकृति के सौंदर्य को दुगुना कर दिया है। कविता में टर – टर ,कण – कण, तृण – तृण, म्यव – म्यव, पीउ – पीउ शब्द के प्रयोग से, तो कहीं अर्थ के चमत्कार से (थम – थम दिन के तम में) तो कहीं शब्द – अर्थ दोनों के चमत्कार से (झम – झम – झम मेघ) प्रकृति की सुंदरता का अद्भुत चित्रण किया है। इस प्रकार अन्य कोई भी कवि प्रकृति सौंदर्य का चित्रण करने में असमर्थ है। इसीलिए पंतजी को प्रकृति सौंदर्य चित्रण का बेजोड़ कवि कहा गया है।

प्रश्न 5.
सावन में पेड़ – पौधे, पशु – पक्षी और मनुष्य खुशी से झूम उठते हैं। कारण बताइए।
उत्तर:
वर्षा होने पर ही पानी मिलता है। हर प्राणी.को जीवन जीने के लिए पानी ज़रूरी है। रोज़मर्रा की ज़रूरतों को पूरी करने के लिए भी पानी अत्यंत आवश्यक है। जैसे – प्यास बुझाने के लिए, हाथ – मुँह धोने के लिए, नहाने – धोने के लिए, कारखानों के लिए, गृह – निर्माण के लिए, बिजली के उत्पादन के लिए, आग बुझाने के लिए, खेती के लिए, यहाँ तक कि पानी बरसने के लिए भी पानी की आवश्यकता पड़ती है। इस प्रकार सभी प्राणियों के लिए जीवन का आधार है – वर्षा और सिर्फ वर्षा।

प्रश्न 5.
वर्षा के कारण प्रकृति में कौन – कौन से परिवर्तन होते हैं?
उत्तर:
वर्षा के कारण प्रकृति में ये परिवर्तन होते हैं – आसमान में काले – काले बादल छा जाते हैं । थम – थमाते दिन में भी अंधेरा फैल जाता है । मेघों के टकराने से बिजली चमक उठती है । मेघों से गर्जना निकलती है । वर्षा के कारण प्रकृति में हरियाली छा जाती है । वर्षा के कारण धरती की शोभा बढती है । वर्षा के दिनों में मनमोहने वाला इन्द्रधनुष भी निकलता है ।

प्रश्न 6.
अधिक वर्षा के कारण किस प्रकार के नुकसान हो सकते हैं?
उत्तर:

• अधिक वर्षा के कारण अनेक प्रकार के नुकसान होते हैं – जैसे
• खेत सढ़ जाते हैं | इससे फसल खराब हो जाते हैं । अधिक वर्षा के कारण बाढ आता है ।
• बाढ के कारण रवाना एवं यातायात की स्थिति खराब हो जाती है ।
• घर – मकान आदि डूब जाते हैं । इसलिए लाखों लोग निराश्रय हो जाते हैं ।
• साग – सब्जी, तरकारियाँ आदि नष्ट हो जाते हैं । जिससे खाद्य पदार्थों की कमी हो जाती है ।
• तालाब, नदी, नालें आदि एकत्रित हो जाते हैं |

प्रश्न 7.
सारी प्रकृति वर्षा पर निर्भर है । कैसे?
उत्तर:
सारी प्रकृति वर्षा पर निर्भर है । वर्षा से प्रकृति सुंदर लगती है । वर्षा से प्रकृति में हरियाली व्याप्त होती है । वर्षा के कारण तालाब, नाल, नदियाँ आदि पानी से भरे रहते हैं । प्रकृति में नयी शोभा आती है। पीने के लिए और खेतीबाडी के लिए पानी इकट्ठा किया जाता है । इसलिए हम कह सकते हैं कि सारी प्रकृति वर्षा पर निर्भर है।

प्रश्न 8.
वर्षा प्राणियों के लिए वरदान है । क्यों?
उत्तर:
वर्षा प्राणियों के लिए वरदान है । पानी के बिना हम जीवित नहीं रह सकते । वर्षा हमारे जीवन का आधार है । पशु-पक्षी और मनुष्य एवं प्रकृति वर्षा से पुलकित होते हैं । ये सब जीवन के लिए वर्षा पर निर्भर रहते हैं। हमारा फ़सलों भी वर्षा के कारण ही उगता है । इसलिए हम कह सकते हैं कि वर्षा प्राणियों के लिए वरदान है ।

प्रश्न 9.
वर्षा से क्या – क्या लाभ हैं?
उत्तर:
वर्षा से हमें कई लाभ हैं । जैसे –

• वर्षा से पीने का पानी इकट्ठा किया जा सकता है । वर्षा से खेतीबाडी की जाती है ।
• वर्षा से सूरज का तापमान दूर किया जा सकता है ।
• वर्षा पशु-पक्षी और मनुष्यों का जीवन आधार है ।
• पेड़ – पौधों के लिए भी वर्षा आधार है।
• वर्षा के कारण ही नदियाँ जीव नदियों के रूप में बहती हैं |
• वर्षा के पानी को बाँधों में इकट्ठा करके बिजली पैदा की जा सकती है ।

प्रश्न 10.
मानव जीवन में वर्षा का क्या महत्व है?
उत्तर:
मानव जीवन में वर्षा का महत्व बहुत अधिक है । वर्षा के बिना सारी प्रकृति निर्जीव तथा सूनी लगती है।

• वर्षा से हमें कई लाभ हैं । जैसे –
• वर्षा से पीने का पानी इकट्ठा किया जा सकता है।
• वर्षा से खेतीबाडी की जाती है ।
• वर्षा से सूरज का तापमान दूर किया जा सकता है ।
• वर्षा पशु-पक्षी और मनुष्यों का जीवन आधार है । पेड़ – पौधों के लिए भी वर्षा आधार है।
• वर्षा के कारण ही नदियाँ जीव नदियों के रूप में बहती हैं।
• वर्षा के पानी को बाँधों में इकट्ठा करके बिजली पैदा की जा सकती है ।

प्रश्न 11.
वर्षा को देखकर सभी प्राणी पुलकित हो जाते हैं । क्यों?
उत्तर:
वर्षा प्रकृति में नयी शोभा लाती है । वर्षा के कारण प्रकृति हरी – भरी रहती है | चारों ओर हरियाली छा जाती है । पशु – पक्षी वर्षा को देखकर संतोष से उछल – कूद पडते हैं । ग्रीष्म ऋतु के कारण अब तक जो ताप को पशु – पक्षी और सारे मनुष्य सह लिये हैं । वे अब वर्षा को देखकर अपने ताप को शांत करने पुलकित हो जाते हैं।

प्रश्न 12.
वर्षा के कारण प्रकृति में कौन – कौन से परिवर्तन होते हैं?
उत्तर:
वर्षा के कारण प्रकृति में ये परिवर्तन होते हैं – आसमान में काले – काले बादल छा जाते हैं । थम – थमाते दिन में भी अंधेरा फैल जाता है | मेघों के टकराने से बिजली चमक उठती है | मेघ गर्जना निकलता है। वर्षा के कारण प्रकृति में हरियाली छा जाती है । वर्षा के कारण धरती की शोभा बढ़ती है । वर्षा के दिनों में मनमोहने वाले इंद्रधनुष भी निकलता है।

प्रश्न 13.
कवि जीवन में सावन को बार – बार क्यों आमंत्रित करते हैं ?
उत्तर:
प्रायः सभी लोग सावन को बार – बार आना बहुत पसंद करते हैं ।

• सावन के ऋतु में ही वर्षा का आरंभ होता है |
• वर्षा ऋतु में पाकृतिक रमणीयता सुंदर होती है ।
• पेड – पौधे, पशु – पक्षी, मनुष्य और यहाँ तक कि धरती भी खुशी से इस ऋतु में झूम उठती है ।
• सावन मन को भाता है।
• इसलिए सभी लोग सावन को बार – बार आना बहुत पसंद करते हैं । उसी प्रकार कवि भी जीवन में सावन को बार – बार आमंत्रित करते हैं।

प्रश्न 14.
खेतीबाडी के लिए वर्षा की आवश्यकता है – इस पर अपने विचार प्रकट कीजिए ।
उत्तर:

• खेतीबाडी के लिए वर्षा की आवश्यकता है ।
• वर्षा के बिना खेतीबाडी करना असंभव है | भारत कृषि प्रधान देश है ।
• खेतीबाडी ही भारतीयों के मुख्य जीवन आधार है।
• फसल उगने के लिए पानी की आवश्यकता है ।
• पानी के बिना सिंचाई नहीं होती । पानी का मुख्य आधार वर्षा ही है ।
• भारत में वर्षा के पानी को इकट्ठा करके नालों के द्वारा सिंचाई हो रही है ।
• बीज बोने से लेकर फसल उगने तक खेतीबाडी के लिए वर्षा की आवश्यकता है ।

प्रश्न 15.
वर्षा के अभाव में प्राणि – जगत की स्थिति कैसी होती है ? (होगी)
उत्तर:

• वर्षा के अभाव से प्राणि जगत की स्थिति बहुत बुरी होती है ।
• वर्षा के अभाव से अकाल उत्पन्न होता है | सबकी प्यास बुझाना मुश्किल हो जाता है ।
• पशु – पक्षी, सकल जीव, मनुष्य जगत यहाँ तक कि पृथ्वी भी पानी के मारे सूख जाते हैं ।
• फ़सल की स्थिति बहुत बुरी होती है ।
• तालाब, नालें, नदियाँ, झील, झरने आदि सब सूख जाते हैं ।

अभिव्यक्ति-सृजनात्मकता

8 Marks Questions and Answers

निम्नलिखित प्रश्नों के उत्तर आठ – दस पंक्तियों में लिखिए।

प्रश्न 1.
पंत जी प्रकृति सौंदर्य के चित्रण में बेजोड कवि है | बरसते बादल पाठ के द्वारा सिद्ध कीजिए।
(या)
वर्षा के समय प्रकृति की सुंदरता दर्शनीय होती है। ‘बरसते बादल’ पाठ के आधार पर इस कथन को सिद्ध कीजिए।
उत्तर:
“बरसते बादल” नामक कविता के कवि हैं श्री सुमित्रानंदन पंत । प्रस्तुत इस कविता पाठ में आप बच्चों में प्रकृति के प्रति प्रेम उत्पन्न कराते हैं । इस कविता में प्रकृति का रमणीय तथा सुंदर चित्रण है।

वर्षा ऋतु हमेशा से सबकी प्रिय ऋतु रही है । वर्षा के समय प्रकृति की सुंदरता देखने लायक होती है। पेड़ – पौधे, पशु – पक्षी, मनुष्य और यहाँ तक कि धरती भी खुशी से झूम उठती है ।

सावन (श्रावण) के मेघ आसमान में झम – झम – झम बरसते हैं । बूंदें छम – छम पेडों पर गिरती हैं। चम – चम बिजली चमक रही है । जिसके कारण अंधेरा होने पर भी उजाला है ।

दादुर टर – टर करते रहते हैं । झिल्ली झन – झन बजती है मोर म्यव – म्यव नाच दिखाते हैं । चातक के गण “पीउ” “पीउ” कहता मेघों की ओर देख रहे हैं । आर्द सुख से क्रंदन करते सोनबालक उड़ते हैं । मेघ गगन में गर्जन करते घुमड – घुमड़ कर गिर रहे हैं ।

वर्षा की बूंदों से रिमझिम – रिमझिम का स्वर निकल रहा है । उन्हें छूने पर किसी भेद के बिना सबके रोम सिहर उठते हैं । वर्षा की धाराओं पर धाराएँ धरती पर झरती हैं । इस कारण मिट्टी के कण – कण से तृण – तृण (कोमल अंकुर) फूट रहे हैं ।

कवि कहते हैं कि वर्षा की धाराओं को पकडने से उसका मन झूलता है । वह सबको संबोधित करते हुए कहते हैं कि उसे घेर ले और सावन के गीत गालें । इंद्रधनुष के झूले में सब मिलकर झूलें । अंत में कवि यह सावन जीवन में फिर – फिर आकर मनभावन करने के लिए कहते हैं ।

इसलिए इस कविता के सारांश के आधार पर हम कह सकते हैं कि पंतजी प्रकृति सौंदर्य चित्रण में बेजोड कवि हैं।

प्रश्न 2.
“सुमित्रानंदन पंतजी प्रकृति चित्रण में बेजोड़ कवि हैं।” – बरसते बादल कविता के द्वारा सिद्ध कीजिए।
उत्तर:

• सुमित्रानंदन पंत हिंदी के राष्ट्र कवि हैं।
• वे प्रकृति चित्रण के बेजोड़ कवि माने जाते हैं।
• आसमान में बादल झम – झम बरसते हैं। छम – छम – छम बूंदें पेड़ों से गिरते हैं।
• बिजली आसमान के हृदय में चमक रही है।
• उस समय दिन में अंधेरा होता है। हृदय के सपने जग जाते हैं।
• सावन के मौसम में दादुर टर – टर करते हैं। झिल्ली – झींगुर बजने लगते हैं।
• मोर म्यव – म्यव करते हैं, चातक गण पीऊ – पीऊ कहते हैं।
• आसमान में मेघ घुमड – घुमड कर गर्जन करते हैं।
• रिमझिम – रिमझिम पानी बरसाता है, वर्षा की बूंदें ज़मीन पर गिरते हैं।
• वर्षा की बूंदें शरीर पर पड़ते ही रोम सिहर उठते हैं। – रज के कण – कण में तृण – तृण पुलकित हो जाते हैं।
• वर्षा की धारा देखकर कवि का मन झूलता है।
• सब लोग मिलकर सावन के गीत गाते हुए सावन का आहवान करते हैं।

प्रश्न 3.
कवि बार – बार अपने जीवन में सावन के आने की कामना कर रहा है। क्यों?
उत्तर:
कवि चाहते हैं कि जीवन में सावन बार-बार आये और सब मिलकर झूलों में झूलें। क्योंकि वर्षा ऋतु हमेशा सबकी प्रिय ऋतु रही है। वर्षा के समय प्रकृति की सुंदरता देखने लायक होती है। पेड – पौधे, पशु – पक्षी, मनुष्य और यहाँ तक कि धरती भी खुशी से झूम उठती हैं।

वर्षा की धाराओं के कारण मिट्टी के कण – कण से कोमल अंकुर फूट कर तृण बन जाते हैं। उस वर्षा के पानी को पाकर सभी का मन झूलने लगता है। कवि कहते हैं कि इन्द्रधनुष को झूला बनाकर हम सब मिलकर आकाश में झूलना चाहते हैं। ऐसी सुंदर – सुंदर घटनाओं के कारण से कवि फिर – फिर वर्षा ऋतु का आगमन करना चाहते हैं।

प्रश्न 4.
बादलों के बरसने से सभी प्राणी प्रसन्नता क्यों प्रकट करते हैं?
उत्तर:
बरसते बादल कविता के कवि श्री सुमित्रानंदन पंत है। इन्हें चिदंबरा काव्य संकलन पर ज्ञानपीठ पुरस्कार से सम्मानित किया गया।

• वर्षा सभी प्राणियों के लिए जीवन का आधार है। प्रकृति का हर प्राणी पानी के बिना रह नहीं सकता।
• पशु – पक्षी और मनुष्य एवं प्रकृति वर्षा से पुलकित होते हैं।
• वर्षा के कारण प्रकृति हरी – भरी रहती है। पशु – पक्षी वर्षा को देखकर संतोष से उछल – कूद पडते हैं।
• ग्रीष्म ऋतु के कारण अब तक जो ताप को पशु – पक्षी और सारे मनुष्य सहलिये हैं, वे अब वर्ष को देखकर अपने – अपने ताप को शांत करने पुलकित हो जाते हैं।
• वर्षा के कारण दादुर, झिल्ली, मोर, चातक और सोनबालक आदि जीव जाति आनंद से पुलकित होते
• वर्षा से पेड – पौधे अपने थकावट को दूर करने के लिए आनंद से झूम उठते हैं।
• वर्षा से पृथ्वी, तालाबें, नदियाँ, झील, झरने आदि प्रसन्नता से अपने सूखेपन को बदल लेते हैं।
• सभी प्राणी अपने – अपने प्यास बुझाने के लिए बादलों के बरसने को प्रसन्नता से निमंत्रण करते हैं।

AP State Syllabus SSC 10th Class Maths Solutions 13th Lesson Probability Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 13 Probability Optional Exercise Textbook Questions and Answers.

10th Class Maths 13th Lesson Probability Optional Exercise Textbook Questions and Answers

Question 1.
Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
(i) the same day?
(ii) consecutive days?
(iii) different days?
Answer:
Shyam and Ekta can visit the shop in the following combination:

(T Tu) (W, Tu) (Th, Tu) (F, Tu) (S, Tu) (Tu, W) (W, W) (Th, W) (F, W) (S, W) (Tu, Th) (W, Th) (Th, F) (F, Th) (S, Th) (Tu, F) (W, F) (Th, S) (F, F) (S, F) (Tu, S) (W, S) (Th, Th) (F, S) (S, S)
∴ Number of total outcomes = 5 × 5 = 5² = 25 [also from the above table]
i) Number of favourable outcomes to that of visiting on the same day
(Tu, Tu), (W, W), (Th, Th), (F, F), (S, S) = 5
∴ Probability of visiting the shop on the same day = [latex]\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}[/latex] = [latex]\frac{5}{25}[/latex] = [latex]\frac{1}{5}[/latex]
ii) Number of outcomes favourable to consecutive days
(Tu, W), (W, Th), (Th, F), (F, S), (W, Tu), (Th, W), (F, Th), (S, F) = 8
∴ Probability of visiting the shop on consecutive days = [latex]\frac{8}{25}[/latex]
iii) If P(E) is the probability of visiting the shop on the same day,
then P([latex]\overline{\mathrm{E}}[/latex]) is the probability of visiting the shop not on the same day.
i.e., P([latex]\overline{\mathrm{E}}[/latex]) is the probability of visiting the shop on different days.
Such that P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = 1
P([latex]\overline{\mathrm{E}}[/latex]) = 1 – P(E) = 1 – [latex]\frac{1}{5}[/latex] = [latex]\frac{4}{5}[/latex]

Question 2.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Answer:
Number of red balls in the bag = 5 As the probability of blue balls is double the probability of red balls, we have that number of blue balls is double the number of red balls.
∴ Blue balls = 5 × 2 = 10.
[!! Let the number of blue balls = x
Number of red balls = 5
Total no. of balls = x + 5
Total outcomes in drawing a ball at random = x + 5
Number of outcomes favourable to red ball = 5
∴ P(R) = [latex]\frac{5}{x+5}[/latex]
from the problem,
P(B) = 2 × [latex]\frac{5}{x+5}[/latex] = [latex]\frac{10}{x+5}[/latex]
Also [latex]\frac{5}{x+5}[/latex] + [latex]\frac{10}{x+5}[/latex] = 1
[∵ P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = 1]
⇒ [latex]\frac{5+10}{x+5}[/latex] = 1
⇒ [latex]\frac{15}{x+5}[/latex] = 1
⇒ x + 5 = 15]

Question 3.
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Answer:
Number of black balls = x
Total number of balls in the box = 12
Probability of drawing a black ball = [latex]\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}[/latex] = [latex]\frac{x}{12}[/latex] …….. (1)
When 6 more black balls are placed in the box, number of favourable outcomes to black ball becomes = x + 6.
Total number of balls in the box becomes = 12 + 6 = 18.
Now the probability of drawing a black ball become = [latex]\frac{x+6}{18}[/latex] …….. (1)
By Problem,
[latex]\frac{x+6}{18}[/latex] = 2. [latex]\frac{x}{12}[/latex]
⇒ [latex]\frac{x+6}{18}[/latex] = [latex]\frac{x}{6}[/latex]
⇒ 6(x + 6) = 18(x)
⇒ 6x + 36 = 18x
⇒ 18x – 6x = 36
⇒ 12x = 36
⇒ x = [latex]\frac{36}{12}[/latex] = 3
Check:

and hence proved.

Question 4.
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is 2/3. Find the number of blue marbles in the jar.
Answer:
Total number of marbles in the jar = 24.
Let the number of green marbles = x.
Then number of blue marbles = 24 – x.
Probability of drawing a green marbles = [latex]\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}[/latex] = [latex]\frac{x}{24}[/latex]
By problem,
[latex]\frac{x}{24}[/latex] = [latex]\frac{2}{3}[/latex]
⇒ 3x = 24 × 2
x = [latex]\frac{24 \times 2}{3}[/latex] = 16
∴ Number of green marbles = 16
Number of blue marbles = 24 – 1 = 8
∴ Probability of picking blue marble = [latex]\frac{8}{24}[/latex] = [latex]\frac{1}{3}[/latex]
(OR)
P(B) = P(E) – P(G) = 1 – [latex]\frac{2}{3}[/latex] = [latex]\frac{1}{3}[/latex]
[!! P(G) = [latex]\frac{2}{3}[/latex]
P(G) + P(B) = 1
∴ P(B) = 1 – P(G) = 1 – [latex]\frac{2}{3}[/latex] = [latex]\frac{1}{3}[/latex]
Number of blue marbles in the jar = [latex]\frac{1}{3}[/latex] × 24 = 8]

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry Ex 11.3 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry Exercise 11.3

10th Class Maths 11th Lesson Trigonometry Ex 11.3 Textbook Questions and Answers

Question 1.
Evaluate:
i) [latex s=2]\frac{\tan 36^{\circ}}{\cot 54^{\circ}}[/latex]
Answer:
Given that [latex s=2]\frac{\tan 36^{\circ}}{\cot 54^{\circ}}[/latex]
= [latex s=2]\frac{\tan 36^{\circ}}{\cot \left(90^{\circ}-36^{\circ}\right)}[/latex] [∵ cot (90 – θ) = tan θ]
= [latex s=2]\frac{\tan 36^{\circ}}{\tan 36^{\circ}}[/latex]
= 1

ii) cos 12° – sin 78°
Answer:
Given that cos 12° – sin 78°
= cos 12° – sin(90° – 12°) [∵ sin (90 – θ) = cos θ]
= cos 12° – cos 12° = 0

iii) cosec 31° – sec 59°
Answer:
Given that cosec 31° – sec 59°
= cosec 31° – sec (90° – 31°) [∵ sec (90 – θ) = cosec θ]
= cosec 31° – cosec 31° = 0

iv) sin 15° sec 75°
Answer:
Given that sin 15° sec 75°
= sin 15° . sec (90° – 15°)
= sin 15° . cosec 15° [∵ sec (90 – θ) = cosec θ]
= sin 15° . [latex]\frac{1}{\sin 15^{\circ}}[/latex] [∵ cosec θ = [latex]\frac{1}{\sin \theta}[/latex]]
= 1

v) tan 26° tan 64°
Answer:
Given that tan 26° tan 64°
= tan 26° . tan (90° – 26°)
= tan 26° . cot 26° [∵ tan (90 – θ) = cot θ]
= tan 26° . [latex]\frac{1}{\tan 26^{\circ}}[/latex] [∵ cot θ = [latex]\frac{1}{\tan \theta}[/latex]]
= 1

Question 2.
Show that
i) tan 48° tan 16° tan 42° tan 74° = 1
Answer:
L.H.S. = tan 48° tan 16° tan 42° tan 74°
= tan 48°. tan 16° . tan(90° – 48°) . tan(90° – 16°)
= tan 48° . tan 16° . cot 48° . cot 16° [∵ tan (90 – θ) = cot θ]
= tan 48° . tan 16° . [latex]\frac{1}{\tan 48^{\circ}}[/latex] . [latex]\frac{1}{\tan 16^{\circ}}[/latex] [∵ cot θ = [latex]\frac{1}{\tan \theta}[/latex]]
= 1 = R.H.S.
∴ L.H.S. = R.H.S.

ii) cos 36° cos 54° – sin 36° sin 54° = 0
Answer:
L.H.S. = cos 36° cos 54° – sin 36° sin54°
= cos (90° – 54°) . cos (90° – 36°) – sin 36° . sin 54° [∵ cos (90 – θ) = sin θ]
= sin 54° . sin 36° – sin 36° . sin 54°
= 0 = R.H.S.
∴ L.H.S. = R.H.S.

Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle. Find the value of A.
Answer:
Given that tan 2A = cot (A – 18°)
⇒ cot (90° – 2A) = cot (A – 18°) [∵ tan θ = cot (90 – θ)]
⇒ 90° – 2A = A – 18°
⇒ 108° = 3A
⇒ A = [latex]\frac{108^{\circ}}{3}[/latex] = 36°
Hence the value of A is 36°.

Question 4.
If tan A = cot B where A and B. are acute angles, prove that A + B = 90°.
Answer:
Given that tan A = cot B
⇒ cot (90° – A) = cot B [∵ tan θ = cot (90 – θ)]
⇒ 90° – A = B
⇒ A + B = 90°

Question 5.
If A, B and C are interior angles of a triangle ABC, then show that [latex]\tan \left(\frac{\mathbf{A}+\mathbf{B}}{2}\right)=\cot \frac{\mathbf{C}}{2}[/latex]
Answer:
Given A, B and C are interior angles of right angle triangle ABC then A + B + C = 180°.
On dividing the above equation by ‘2’ on both sides, we get 180°

On taking tan ratio on both sides

Hence proved.

Question 6.
Express sin 75° + cos 65° in terms of trigonometric ratios of angles between 0° and 45°.
Answer:
We have sin 75° + cos 65°
= sin (90° – 15°) + cos (90° – 25°)
= cos 15° + sin 25° [∵ sin (90 – θ) = cos θ and cos (90 – θ) = sin θ]

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.3 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.3

10th Class Maths 6th Lesson Progressions Ex 6.3 Textbook Questions and Answers

Question 1.
Find the sum of the following APs:
i) 2, 7, 12,…, to 10 terms.
Answer:
Given A.P: 2, 7, 12, …… to 10 terms
a = 2; d = a₂ – a₁ = 7 – 2 = 5; n = 10
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
∴ S₁₀ = [latex]\frac{10}{2}[/latex][2 × 2 + (10 – 1)5]
= 5 [4 + 9 × 5]
= 5 [4 + 45]
= 5 × 49
= 245

ii) -37, -33, -29,…, to 12 terms.
Answer:
Given A.P: -37, -33, -29,…, to 12 terms.
a = -37; d = a₂ – a₁ = (-33) – (-37) = -33 + 37 = 4; n = 12
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
∴ S₁₂ = [latex]\frac{12}{2}[/latex][2 × (-37) + (12 – 1)4]
= 6 [-74 + 11 × 4]
= 6 [-74 + 44]
= 6 × (-30)
= -180

iii) 0.6, 1.7, 2.8,…, to 100 terms.
Answer:
Given A.P : 0.6, 1.7, 2.8,…. S₁₀₀
a = 0.6; d = a₂ – a₁ = 1.7 – 0.6 = 1.1; n = 100
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
∴ S₁₀₀ = [latex]\frac{100}{2}[/latex][2 × 0.6 + (100 – 1)1.1]
= 50 [1.2 + 99 × 1.1]
= 50 [1.2 + 108.9]
= 50 × 110.1
= 5505

iv) [latex]\frac{1}{15}[/latex], [latex]\frac{1}{12}[/latex], [latex]\frac{1}{10}[/latex],…, to 11 terms.
Answer:
Given A.P: [latex]\frac{1}{15}[/latex], [latex]\frac{1}{12}[/latex], [latex]\frac{1}{10}[/latex],…, S₁₁
a = [latex]\frac{1}{15}[/latex]; d = a₂ – a₁ = [latex]\frac{1}{12}[/latex] – [latex]\frac{1}{15}[/latex] = [latex]\frac{5-4}{60}[/latex] = [latex]\frac{1}{60}[/latex]; n = 11
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]

2. Find the sums given below =:
i) 7 + 10[latex]\frac{1}{2}[/latex] + 14 + …. + 84
Answer:
Given A.P : 7 + 10[latex]\frac{1}{2}[/latex] + 14 + …. + 84
a = 7; d = a₂ – a₁ = 10[latex]\frac{1}{2}[/latex] – 7 = 3[latex]\frac{1}{2}[/latex] and the last term l = a_n = 84
But, a_n = a + (n – 1) d
∴ 84 = 7 + (n – 1) 3[latex]\frac{1}{2}[/latex]
⇒ 84 – 7 = (n – 1) × [latex]\frac{7}{2}[/latex]
⇒ n – 1 = 77 × [latex]\frac{2}{7}[/latex] = 22
⇒ n = 22 + 1 = 23
Now, S_n = [latex]\frac{n}{2}[/latex](a + l) where a = 7; l = 84
S₂₃ = [latex]\frac{23}{2}[/latex](7 + 84)
= [latex]\frac{23}{2}[/latex] × 91
= [latex]\frac{2093}{2}[/latex]
= 1046[latex]\frac{1}{2}[/latex]

ii) 34 + 32 + 30 + … + 10
Answer:
Given A.P: 34 + 32 + 30 + … + 10
a = 34; d = a₂ – a₁ = 32 – 34 = -2 and the last term l = a_n = 10
But, a_n = a + (n – 1) d
∴ 10 = 34 + (n – 1) (-2)
⇒ 10 – 34 = -2n + 2
⇒ -2n = -24 – 2
⇒ n = [latex]\frac{-26}{-2}[/latex] = 13
∴ n = 13
Also, S_n = [latex]\frac{n}{2}[/latex](a + l)
where a = 34; l = 10
S₁₃ = [latex]\frac{13}{2}[/latex](34 + 10)
= [latex]\frac{13}{2}[/latex] × 44
= 13 × 22
= 286

iii) -5 + (-8) + (-11) + … + (-230)
Answer:
Given A.P: -5 + (-8) + (-11) + … + (-230)
Here first term, a = -5;
d = a₂ – a₁ = (-8) – (-5) = -8 + 5 = -3 and the last term l = a_n = 10
But, a_n = a + (n – 1) d
∴ (-230) = -5 + (n – 1) (-3)
⇒ -230 + 5 = -3n + 3
⇒ -3n + 3 = -225
⇒ -3n = -225 – 3
⇒ 3n = 228
⇒ n = [latex]\frac{228}{3}[/latex] = 76
∴ n = 76
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
where a = -5; l = -230
S₇₆ = [latex]\frac{76}{2}[/latex]((-5) + (-230))
= 38 × (-235)
= -8930

Question 3.
In an AP:
i) Given a = 5, d = 3, a_n = 50. find n and S_n.
Answer:
Given :
a = 5; d = 3;
a_n = a + (n – 1)d = 50
⇒ 50 = 5 + (n – 1) 3
⇒ 50 – 5 = 3n – 3
⇒ 3n = 45 + 3
⇒ n = [latex]\frac{48}{3}[/latex] = 16
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
S₁₆ = [latex]\frac{16}{2}[/latex](5 + 50)
= 38 × 55
= 440

ii) Given a = 7, a₁₃ = 35, find d and S₁₃.
Answer:
Given: a = 7;
a₁₃ = a + 12d = 35
⇒ 7 + 12d = 35
⇒ 12d = 35 – 7
⇒ n = [latex]\frac{28}{12}[/latex] = [latex]\frac{7}{3}[/latex]
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
S₁₃ = [latex]\frac{13}{2}[/latex](7 + 35)
= [latex]\frac{13}{2}[/latex] × 42
= 13 × 21
= 273

iii) Given a₁₂ = 37, d = 3 find a and S₁₂.
Answer:
Given:
a₁₂ = a + 11d = 37
d = 3
So, a₁₂ = a + 11 × 3 = 37
⇒ a + 33 = 37
⇒ a = 37 – 33 = 4
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
S₁₂ = [latex]\frac{12}{2}[/latex](4 + 37)
= 6 × 41
= 246

iv) Given a₃ = 15, S₁₀ = 125, find d and a₁₀.
Answer:
Given:
a₃ = a + 2d = 15
⇒ a = 15 – 2d ……… (1)
S₁₀ = 125 but take S₁₀ as 175
i.e., S₁₀ = 175
We know that,

⇒ 35 = 2 (15 – 2d) + 9d [∵ a = 15 – 2d]
⇒ 35 = 30 – 4d + 9d
⇒ 35 – 30 = 5d
⇒ d = [latex]\frac{5}{5}[/latex] = 1
Substituting d = 1 in equation (1) we get
a = 15 – 2 × 1 = 15 – 2 = 13
Now, a_n = a + (n – 1) d
a₁₀ = a + 9d = 13 + 9 × 1 = 13 + 9 = 22
∴ a₁₀ = 22; d = 1

v) Given a = 2, d = 8, S_n = 90, find n and a_n.
Answer:
Given a = 2, d = 8, S_n = 90
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]

⇒ 90 = 2n [2n – 1]
⇒ 4n² – 2n = 90
⇒ 4n² – 2n – 90 = 0
⇒ 2(2n² – n – 45) = 0
⇒ 2n² – n – 45 = 0
⇒ 2n² -10n + 9n – 45 = 0
⇒ 2n(n – 5) + 9(n – 5) = 0
⇒ (n – 5)(2n + 9) = 0
⇒ n – 5 = 0 (or) 2n + 9 = 0
⇒ n = 5 (or) n = [latex]\frac{-9}{2}[/latex] (discarded)
∴ n = 5
Now a_n = a₅ = a + 4d = 2 + 4 x 8
= 2 + 32 = 34

vi) Given a_n = 4, d = 2, S_n = -14, find n and a.
Answer:
Given a_n = a + (n – 1) d = 4 ……. (1)
d = 2; S_n = – 14
From (1); a + (n – 1) 2 = 4
a = 4 – 2n + 2
a = 6 – 2n
Given a = 2, d = 8, S_n = 90
S_n = [latex]\frac{n}{2}[/latex][a + a_n]
-14 = [latex]\frac{n}{2}[/latex][(6-2n) + 4] [∵ a = 6 – 2n]
-14 × 2 = n (10 – 2n)
⇒ 10n – 2n² = – 28
⇒ 2n² – 10n – 28 = 0
⇒ n² – 5n – 14 = 0
⇒ n² – 7n + 2n – 14 = 0
⇒ n (n – 7) + 2 (n – 7) = 0
⇒ (n – 7) (n + 2) = 0
⇒ n = 7 (or) n = – 2
∴ n = 7
Now a = 6 – 2n = 6 – 2 × 7
= 6 – 14 = -8
∴ a = – 8; n = 7

vii) Given l = 28, S = 144, and there are total 9 terms. Find a.
Answer:
Given:
l = a₉ = a + 8d = 28 and S₉ = 144 But,
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
144 = [latex]\frac{9}{2}[/latex](a + 28)
⇒ 144 × [latex]\frac{2}{9}[/latex] = a + 28
⇒ a + 28 = 32
⇒ a = 4

Question 4.
The first and the last terms of an A.P are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Answer:
Given A.P in which a = 17
Last term = l = 350
Common difference, d = 9
We know that, a_n = a + (n – 1) d
350 = 17 + (n- 1) 9
⇒ 350 = 17 + 9n – 9
⇒ 9n = 350 – 8
⇒ n = [latex]\frac{342}{9}[/latex] = 38
Now, S_n = [latex]\frac{n}{2}[/latex](a + l)
S₃₈ = [latex]\frac{38}{2}[/latex](17 + 350)
= 19 × 367 = 6973
∴ n = 38; S_n = 6973

Question 5.
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
Answer:
Given A.P in which

Substituting d = 4 in equation (1),
we get a + 4 = 14
⇒ a = 14 – 4 = 10

Question 6.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
Answer:
Given :
A.P such that S₇ = 49; S₁₇ = 289
We know that,

Substituting d = 2 in equation (1), we get,
a + 3 × 2 = 7
⇒ a = 7 – 6 = 1
∴ a = 1; d = 2

∴ Sum of first n terms S_n = n².
Shortcut: S₇ = 49 = 7²
S₁₇ = 289 = 17²
∴ S_n = n²

Question 7.
Show that a₁, a₂ …,a_n, …. form an AP where a_n is defined as below:
i) a = 3 + 4n
ii) a_n = 9 – 5n. Also find the sum of the first 15 terms in each case.
Answer:
Given a_n = 3 + 4n
Then a₁ = 3 + 4 × l = 3 + 4 = 7
a₂ = 3 + 4 × 2 = 3 + 8 = 11
a₃ = 3 + 4 × 3 = 3 + 12 = 15
a₄ = 3 + 4 × 4 = 3 + 16 = 19
Now the pattern is 7, 11, 15, ……
where a = a₁ = 7; a₂ = 11; a₃ = 15, ….. and
a₂ – a₁ = 11 – 7 = 4;
a₃ – a₂ = 15 – 11 = 4;
Here d = 4
Hence a₁, a₂, ….., a_n ….. forms an A.P.

ii) a_n = 9 – 5n
Given: a_n = 9 – 5n.
a₁ = 9 – 5 × l = 9 – 5 = 4
a₂ = 9 – 5 × 2 = 9 – 10 = -1
a₃ = 9 – 5 × 3 = 9 – 15 = -6
a₄ = 9 – 5 × 4 = 9 – 20 = -11
Also
a₂ – a₁ = -1 – 4 = -5;
a₃ – a₂ = -6 – (-1) = – 6 + 1 = -5
a₄ – a₃ = -11 – (-6) = -11 + 6 = -5
∴ d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = …. = -5
Thus the difference between any two successive terms is constant (or) starting from the second term, each term is obtained by adding a fixed number ‘-5’ to its preceding term.
Hence {a_n} forms an A.P.

Question 8.
If the sum of the first n terms of an AP is 4n – n², what is the first term (remember the first term is S₁)? What is the sum of first two terms? What is the second term? Similarly, find the 3^rd, the 10^th and the n^th terms.
Answer:
Given an A.P in which S_n = 4n – n²
Taking n = 1 we get
S₁ = 4 × 1- 12 = 4 – 1 = 3
n = 2; S₂ = a₁ + a₂ = 4 × 2 – 2² = 8 – 4 = 4
n = 3; S₃ = a₁ + a₂ + a₃ = 4 × 3 -3² = 12 – 9 = 3
n = 4; S₄ = a₁ + a₂ + a₃ + a₄ = 4 × 4 – 4² = 16 – 16 = 0
Hence, S₁ = a₁ = 3
a₂ = S₂ – S₁ = 4 – 3 = 1
a₃ = S₃ – S₂ = 3 – 4 = -1
a₄ = S₄ – S₃ = 0 – 3 = -3
So, d = a₂ – a₁ = l – 3 = -2
Now, a₁₀ = a + 9d  [∵ a_n = a + (n – 1) d]
= 3 + 9 × (- 2)
= 3 – 18 = -15
a_n = 3 + (n – 1) × (-2)
= 3 – 2n + 2
= 5 – 2n

Question 9.
Find the sum of the first 40 positive integers divisible by 6.
Answer:
The given numbers are the first 40 positive multiples of 6
⇒ 6 × 1, 6 × 2, 6 × 3, ….., 6 × 40
⇒ 6, 12, 18, ….. 240
S_n = [latex]\frac{n}{2}[/latex](a + l)
S₄₀ = [latex]\frac{40}{2}[/latex](6 + 240)
= 20 × 246
= 4920
∴ S₄₀ = 4920

Question 10.
A sum of Rs. 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs. 20 less than its preceding prize, find the value of each of the prizes.
Answer:
Given:
Total/Sum of all cash prizes = Rs. 700
Each prize differs by Rs. 20
Let the prizes (in ascending order) be x, x + 20, x + 40, x + 60, x + 80, x + 100, x + 120
∴ Sum of the prizes = S₇ = [latex]\frac{n}{2}[/latex](a + l)
⇒ 700 = [latex]\frac{7}{2}[/latex][x + x + 120]
⇒ 700 × [latex]\frac{2}{7}[/latex] = 2x + 120
⇒ 100 = x + 60
⇒ x = 100 – 60 = 40
∴ The prizes are 160, 140, 120, 100, 80, 60, 40.

Question 11.
In a school, students thought of plant¬ing trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
Answer:
Given: Classes: From I to XII
Section: 3 in each class.
∴ Trees planted by each class = 3 × class number

∴ Total trees planted = 3 + 6 + 9 + 12 + …… + 36 is an A.P.
Here, a = 3 and l = 36; n = 12
∴ S_n = [latex]\frac{n}{2}[/latex](a + l)
S₁₂ = [latex]\frac{12}{2}[/latex][3 + 36]
= 6 × 39
= 234
∴ Total plants = 234

Question 12.
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, … as shown in figure. What is the total length of such a spiral made up of thirteen
consecutive semicircles? (Take π = [latex]\frac{22}{7}[/latex])

[Hint: Length of successive semicircles is l₁, l₂, l₃, l₄,….. with centres at A, B, A, B,…, respectively.]
Answer:
Given: l₁, l₂, l₃, l₄,….., l₁₃ are the semicircles with centres alternately at A and B; with radii
r₁ = 0.5 cm [1 × 0.5]
r₂ = 1.0 cm [2 × 0.5]
r₃ = 1.5 cm [3 × 0.5]
r₄ = 2.0 cm [4 × 0.5] [∵ Radii are in A.P. as aj = 0.5 and d = 0.5]
……………………………
r₁₃ = 13 × 0.5 = 6.5
Now, the total length of the spiral = l₁ + l₂ + l₃ + l₄ + ….. + l₁₃ [∵ 13 given]
But circumference of a semi-cirle is πr.
∴ Total length of the spiral = π × 0.5 + π × 1.0 + ………. + π × 6.5
= π × [latex]\frac{1}{2}[/latex][l + 2 + 3 + ….. + 13]
[∵ Sum of the first n – natural numbers is [latex]\frac{n(n+1)}{2}[/latex]
= [latex]\frac{22}{7} \times \frac{1}{2} \times \frac{13 \times 14}{2}[/latex]
= 11 × 13
= 143 cm.

Question 13.
200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?

Answer:
Given: Total logs = 200
Number of logs stacked in the first row = 20
Number of logs stacked in the second row = 19
Number of logs stacked in the third row = 18
The number series is 20, 19, 18,….. is an A.P where a = 20 and
d = a₂ – a₁ = 19 – 20 = -1
Also, S_n = 200

400 = 41n – n²
⇒ n² – 41n + 400 = 0
⇒ n² – 25n – 16n + 400 = 0
⇒ n(n – 25) – 16(n – 25) = 0
⇒ (n – 25) (n – 16) = 0
⇒ n – 25 (or) 16
There can’t be 25 rows as we are starting with 20 logs in the first row.
∴ Number of rows must be 16.
∴ n = 16

Question 14.
In a bucket and ball race, a bucket is placed at the starting point, which is 5 m from the first ball, and the other balls are placed 3 m apart in a straight line. There are ten balls in the line.

A competitor starts from the bucket, picks up the nearest ball, runs back with it, drops it in the bucket, runs back to pick up the next ball, runs to the bucket to drop it in, and she continues in the same way until all the balls are in the bucket. What is the total distance the competitor has to run?
[Hint: To pick up the first ball and the second ball, the total distance (in metres) run by a competitor is 2 × 5 + 2 × (5 + 3)]
Answer:
Given: Balls are placed at an equal distance of 3 m from one another.
Distance of first ball from the bucket = 5 m
Distance of second ball from the bucket = 5 + 3 = 8 m (5 + 1 × 3)
Distance of third ball from the bucket = 8 + 3 = 11 m (5 + 2 × 3)
Distance of fourth ball from the bucket = 11 + 3 = 14 m (5 + 3 × 3)
………………………………
∴ Distance of the tenth ball from the bucket = 5 + 9 × 3 = 5 + 27 = 32 m.
1st ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 5 = 10 m.
2nd ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 8 = 16 m.
3rd ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 11 = 22 m.
………………………………
10th ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 32 = 64 m.
Total distance = 10 m + 16 m + 22 m + …… + 64 m.
Clearly, this is an A.P in which a = 10; d = a₂ – a₁ = 16 – 10 = 6 and n = 10.
∴ S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
∴ S₁₀ = [latex]\frac{10}{2}[/latex][2 × 10 + (10 – 1)6]
= 5 [20 + 54]
= 5 × 74
= 370 m
∴ Total distance = 370 m.

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.1 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.1

10th Class Maths 6th Lesson Progressions Ex 6.1 Textbook Questions and Answers

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
i) The taxi fare after each km when the fare is Rs. 20 for the first km and rises by Rs. 8 for each additional km.
Answer:
Fare for the first km = Rs. 20 = a
Fare for each km after the first = Rs. 8 = d
∴ The fares would be 20, 28, 36, 44, …….
The above list forms an A.P.
Since each term in the list, starting from the second can be obtained by adding ‘8’ to its preceding term.

ii) The amount of air present in a cylinder when a vacuum pump removes [latex]\frac{1}{4}[/latex]th of the air remaining in the cylinder at a time.
Answer:
Let the amount of air initially present in the cylinder be 1024 lit.
First it removes [latex]\frac{1}{4}[/latex]th of the volume
i.e., [latex]\frac{1}{4}[/latex] × 1024 = 256
∴ Remaining air present in the cylinder = 768
At second time it removes [latex]\frac{1}{4}[/latex]th of 768
i.e., [latex]\frac{1}{4}[/latex] × 768 = 192
∴ Remaining air in the cylinder = 768 – 192 = 576
Again at third time it removes [latex]\frac{1}{4}[/latex]th of 576
i.e., [latex]\frac{1}{4}[/latex] × 576 = 144
Remaining air in the cylinder = 576 – 144 = 432
i.e., the volume of the air present in the cylinder after 1st, 2nd, 3rd,… times is 1024, 768, 576, 432, …..
Here, a₂ – a₁ = 768 – 1024 = – 256
a₃ – a₂ = 576 – 768 = – 192
a₄ – a₃ = 432 – 576 = – 144 .
Thus the difference between any two successive terms is not equal to a fixed number.
∴ The given situation doesn’t show an A.P.

iii) The cost of digging a well, after, every metre of digging, when it costs ? 150 for the first metre and rises by ? 50 for each subsequent metre.
Answer:
Cost for digging the first metre = Rs. 150
Cost for digging subsequent metres = Rs. 50 each.
i.e.,

The list is 150, 200, 250, 300, 350, ……..
Here d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = ……. = 50
∴ The given situation represents an A.P.

iv) The amount of money in the account every year, when Rs. 10000 is deposited at compound interest at 8 % per annum.
Answer:
Amount deposited initially = P = Rs. 10,000
Rate of interest = R = 8% p.a [at C.I.]
∴ [latex]A=P\left(1+\frac{R}{100}\right)^{n}[/latex]

The terms 10800, 11664, 12597.12, ……. a₂ – a₁ = 800
Here, a = 10,000                                     a₃ – a₂ = 864
But, a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃                a₄ – a₃ = 953.12
∴ The given situation doesn’t represent an A.P.

Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
i) a = 10, d = 10
ii) a = -2, d = 0
iii) a = 4, d = – 3
iv) a = – 1, d = 1/2
v) a = – 1.25, d = – 0.25
Answer:

Question 3.
For the following A.Ps, write the first term and the common difference:
i) 3, 1, – 1, – 3,….
ii) – 5, – 1, 3, 7,….
iii) [latex]\frac{1}{3}[/latex], [latex]\frac{5}{3}[/latex], [latex]\frac{9}{3}[/latex], [latex]\frac{13}{3}[/latex], ……..
iv) 0.6, 1.7, 2.8, 3.9,…
Answer:

Question 4.
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
i) 2, 4, 8, 16, …….
ii) 2, [latex]\frac{5}{2}[/latex], 3, [latex]\frac{7}{2}[/latex], …….
iii) – 1.2, – 3.2, – 5.2, – 7.2,……
iv) -10,-6, -2, 2, …….
v) 3, 3 + √2, 3 + 2√2, 3 + 3√2, …….
vi) 0.2, 0.22, 0.222, 0.2222, ……
vii) 0, -4, -8, -12, …….
viii) -[latex]\frac{1}{2}[/latex], -[latex]\frac{1}{2}[/latex], -[latex]\frac{1}{2}[/latex], -[latex]\frac{1}{2}[/latex]
ix) 1, 3, 9, 27,…..
x) a, 2a, 3a, 4a,….
xi) a, a², a³, a⁴, …..
xii) √2, √8, √18, √32, …….
xiii) √3, √6, √9, √12, …….
Answer:

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.5 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.5

10th Class Maths 6th Lesson Progressions Ex 6.5 Textbook Questions and Answers

Question 1.
For each geometric progression find the common ratio ‘r’, and then find a_n.
i) 3, [latex]\frac{3}{2}[/latex], [latex]\frac{3}{4}[/latex], [latex]\frac{3}{8}[/latex], …….
Answer:
Given G.P.: 3, [latex]\frac{3}{2}[/latex], [latex]\frac{3}{4}[/latex], [latex]\frac{3}{8}[/latex], …….

ii) 2, -6, 18, -54, …….
Answer:
Given G.P. = 2, -6, 18, -54, …….
a = 2, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{-6}{2}[/latex] = -3
a_n = a . r^n-1 = 2 × (-3)^n-1
∴ r = -3; a_n = 2(-3)^n-1

iii) -1, -3, -9, -27, ……
Given G.P. = -1, -3, -9, -27, ……
a = -1, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{-3}{-1}[/latex] = 3
a_n = a . r^n-1 = (-1) × 3^n-1
∴ r = 3; a_n = (-1) × 3^n-1

iv) 5, 2, [latex]\frac{4}{5}[/latex], [latex]\frac{8}{25}[/latex], …….
Given G.P. = 5, 2, [latex]\frac{4}{5}[/latex], [latex]\frac{8}{25}[/latex], …….
a = 5, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{2}{5}[/latex]
a_n = a . r^n-1 = 5 × [latex]\left(\frac{2}{5}\right)^{n-1}[/latex]
∴ r = [latex]\frac{2}{5}[/latex]; a_n = 5[latex]\left(\frac{2}{5}\right)^{n-1}[/latex]

Question 2.
Find the 10^th and nth term of G.P.: 5, 25, 125,…..
Answer:
Given G.P.: 5, 25, 125,…..
a = 5, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{25}{5}[/latex] = 5
a_n = a . r^n-1 = 5 × (5)^n-1 = 5^1+n-1 = 5ⁿ
a₁₀ = a . r⁹ = 5 × 5⁹ = 5¹⁰
∴ a₁₀ = 5¹⁰; a_n = 5ⁿ

Question 3.
Find the indicated term of each geometric progression.
i) a₁ = 9; r = [latex]\frac{1}{3}[/latex]; find a₇.
Answer:
a_n = a . r^n-1

ii) a₁ = -12; r = [latex]\frac{1}{3}[/latex]; find a₆.
Answer:
a_n = a . r^n-1

Question 4.
Which term of the G.P.
i) 2, 8, 32,….. is 512?
Answer:
Given G.P.: 2, 8, 32,….. is 512
a = 2, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{8}{2}[/latex] = 4
Let the n^th term of G.P. be 512

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2⁹
∴ 2n – 1 = 9
[∵ bases are equal, exponents are also equal]
∴ 2n = 9 + 1 = 10
n = [latex]\frac{10}{2}[/latex] = 5
∴ 512 is the 5^th term of the given G.P.

ii) √3, 3, 3√3, …….. is 729?
Answer:
Given G.P.: √3, 3, 3√3, …….. is 729
a = √3, r = [latex]\frac{a_{2}}{a_{1}}[/latex] = [latex]\frac{3}{\sqrt{3}}[/latex] = √3
now a_n = a . r^n-1 = 729
⇒ (√3)(√3)^n-1 = 729
⇒ (√3)ⁿ = 3⁶ = (√3)¹²
⇒ n = 12
So 12th term of GP √3, 3, 3√3, …….. is 729.

iii) [latex]\frac{1}{3}[/latex], [latex]\frac{1}{9}[/latex], [latex]\frac{1}{27}[/latex], ……. is [latex]\frac{1}{2187}[/latex]?
Answer:
Given G.P.: [latex]\frac{1}{3}[/latex], [latex]\frac{1}{9}[/latex], [latex]\frac{1}{27}[/latex], ……. is [latex]\frac{1}{2187}[/latex]

Let [latex]\frac{1}{2187}[/latex] be the n^th term of the G.P., then
a_n = a . r^n-1 = [latex]\frac{1}{2187}[/latex]

[∵ bases are equal, exponents are also equal]
7^th term of G.P is [latex]\frac{1}{2187}[/latex].

Question 5.
Find the 12^th term of a G.P. whose 8 term is 192 and the common ratio is 2.
Answer:
Given a G.P. such that a₈ = 192 and r = 2
a_n = a . r^n-1
a₈ = a . (2)^8-1 = 192

= 3 × 2¹⁰ = 3 × 1024 = 3072.

Question 6.
The 4^th term of a geometric progression is [latex]\frac{2}{3}[/latex] and the seventh term is [latex]\frac{16}{81}[/latex]. Find the geometric series.
Answer:
Given: In a G.P.

Now substituting r = [latex]\frac{2}{3}[/latex] in equation (1)
we get,

Question 7.
If the geometric progressions 162, 54, 18, ….. and [latex]\frac{2}{81}[/latex], [latex]\frac{2}{27}[/latex], [latex]\frac{2}{9}[/latex],….. have their n^th term equal, find the value of n.
Answer:
Given G.P.: 162, 54, 18, ….. and [latex]\frac{2}{81}[/latex], [latex]\frac{2}{27}[/latex], [latex]\frac{2}{9}[/latex],……

Given that n^th terms are equal
a_n = a . r^n-1

⇒ 3^n-1+n-1 = 81 × 81
⇒ 3^2n-2 = 3⁴ × 3⁴
⇒ 3^2n-2 = 3⁸ [∵ a^m . aⁿ = a^m+n]
⇒ 2n – 2 = 8
[∵ bases are equal, exponents are also equal]
2n = 8 + 2
⇒ n = [latex]\frac{10}{2}[/latex] = 5
The 5^th terms of the two G.P.s are equal.

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.2 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.2

10th Class Maths 6th Lesson Progressions Ex 6.2 Textbook Questions and Answers

Question 1.
Fill in the blanks in the following table, given that ‘a’ is the first term, d the common difference and an the nth term of the A.P:

Answer:

Question 2.
Find the i) 30th term of the A.P.: 10, 7, 4,……
ii) 11th term of the A.P.: -3, -[latex]\frac{1}{2}[/latex], 2,…
Answer:
i) Given A.P. = 10, 7, 4, …….
a₁ = 10; d = a₂ – a₁ = 7 – 10 = – 3
a_n = a + (n – 1) d
a₃₀ = 10 + (30 – 1) (- 3) = 10 + 29 × (- 3) = 10 – 87 = – 77

ii) Given A.P. = – 3, -[latex]\frac{1}{2}[/latex], 2,…
a₁ = -3; d = a₂ – a₁ = -[latex]\frac{1}{2}[/latex] – (-3) = – 3
= -[latex]\frac{1}{2}[/latex] + 3
= [latex]\frac{-1+6}{2}[/latex]
= [latex]\frac{5}{2}[/latex]
a_n = a + (n – 1) d
= -3 + (11-1) × [latex]\frac{5}{2}[/latex]
= -3 + 10 × [latex]\frac{5}{2}[/latex]
= -3 + 5 × 5
= -3 + 25
= 22

Question 3.
Find the respective terms for the following APs.
i) a₁ = 2; a₃ = 26, find a₂.
Answer:
Given: a₁ = a = 2 …….. (1)
a₃ = a + 2d = 26 …….. (2
Equation (2) – equation (1)
⇒ (a + 2d) – a = 26 – 2
⇒ 2d = 24
d = [latex]\frac{24}{2}[/latex] = 12
Now a₂ = a + d = 2 + 12 = 14

ii) a₂ = 13; a₄ = 3, find a₁, a₃.
Answer:
Given: a₂ = a + d = 13 ….. (1)
a₄ = a + 3d = 3 ….. (2)
Solving equations (1) and (2);

∴ Substituting d = – 5 in equation (1) we get
a + (-5) = 13
∴ a = 13 + 5 = 18 i.e., a₁ = 18
a₃ = a + 2d = 18 + 2(- 5)
= 18 – 10 = 8

iii) a₁ = 5; a₄ = 9[latex]\frac{1}{2}[/latex], find a₂, a₃.
Answer:
Given: a₁ = a = 5 ….. (1)
a₄ = a + 3d = 9[latex]\frac{1}{2}[/latex] ….. (2)
Solving equations (1) and (2);

⇒ 3d = 4[latex]\frac{1}{2}[/latex]
⇒ 3d = [latex]\frac{9}{2}[/latex]
⇒ d = [latex]\frac{9}{2 \times 3}[/latex] = [latex]\frac{3}{2}[/latex]
∴ a₂ = a + d = 5 + [latex]\frac{3}{2}[/latex] = [latex]\frac{13}{2}[/latex]
a₃ = a + 2d = 5 + 2 × [latex]\frac{3}{2}[/latex] = 5 + 3 = 8

iv) a₁ = -4; a₆ = 6, find a₂, a₃, a₄, a₅.
Answer:
Given: a₁ = a = -4 ….. (1)
a₆ = a + 5d = 6 ….. (2)
Solving equations (1) and (2);
(-4) + 5d = 6
⇒ 5d = 6 + 4
⇒ 5d = 10
⇒ d = [latex]\frac{10}{5}[/latex]
Now
∴ a₂ = a + d = -4 + 2 = -2
a₃ = a + 2d = -4 + 2 × 2 = -4 + 4 = 0
a₄ = a + 3d = -4 + 3 × 2 = -4 + 6 = 2
a₅ = a + 4d = -4 + 4 × 2 = -4 + 8 = 4

v) a₂ = 38; a₆ = -22, find a₁, a₃, a₄, a₅.
Answer:
Given: a₂ = a + d = 38 ….. (1)
a₆ = a + 5d = -22 ….. (2)
Subtracting (2) from (1) we get

Now substituting, d = – 15 in equation (1), we get
a + (- 15) = 38 ⇒ a = 38 + 15 = 53
Thus,
a₁ = a = 53;
a₃ = a + 2d = 53 + 2 × (- 15) = 53 – 30 = 23;
a₄ = a + 3d = 53 + 3 × (- 15) = 53 – 45 = 8;
a₅ = a + 4d = 53 + 4 × (- 15) = 53 – 60 = – 7

Question 4.
Which term of the AP:
3, 8, 13, 18,…, is 78?
Answer:
Given: 3, 8, 13, 18, ……
Here a = 3; d = a₂ – a₁ = 8 – 3 = 5
Let ‘78’ be the nth term of the given A.P.
∴ a_n = a + (n – 1) d
⇒ 78 = 3 + (n – 1) 5
⇒ 78 = 3 + 5n – 5
⇒ 5n = 78 + 2
⇒ n = [latex]\frac{80}{2}[/latex] = 16
∴ 78 is the 16th term of the given A.P.

Question 5.
Find the number of terms in each of the following APs:
i) 7, 13, 19, ….., 205
Answer:
Given: A.P: 7, 13, 19, ……….
Here a₁ = a = 7; d = a₂ – a₁ = 13 – 7 = 6
Let 205 be the n^th term of the given A.P.
Then, a_n = a + (n – 1) d
205 = 7 + (n- 1)6
⇒ 205 = 7 + 6n – 6
⇒ 205 = 6n + 1
⇒ 6n = 205 – 1 = 204
∴ n = [latex]\frac{204}{6}[/latex] = 34
∴ 34 terms are there.

ii) 18, 15[latex]\frac{1}{2}[/latex], 13, …, -47
Answer:
Given: A.P: 18, 15[latex]\frac{1}{2}[/latex], 13, …….
Here a₁ = a = 18;
d = a₂ – a₁ = 15[latex]\frac{1}{2}[/latex] – 18 = -2[latex]\frac{1}{2}[/latex] = -[latex]\frac{5}{2}[/latex]
Let ‘-47’ be the nth term of the given A.P.
a_n = a + (n – 1) d

⇒ -94 = 36 – 5n + 5
⇒ 5n = 94 + 41
⇒ n = [latex]\frac{135}{5}[/latex] = 27
∴ 27 terms are there.

Question 6.
Check whether, -150 is a term of the AP: 11, 8, 5, 2…
Answer:
Given: A.P. = 11, 8, 5, 2…
Here a₁ = a = 11;
d = a₂ – a₁ = 8 – 11 = -3
If possible, take – 150 as the n^th term of the given A.P.
a_n = a + (n – 1) d
⇒ -150 = 11 + (n – 1) × (-3)
⇒ -150 = 11 – 3n + 3
⇒ 14 – 3n = – 150
⇒ 3n= 14 + 150 = 164
∴ n = [latex]\frac{164}{3}[/latex] = 54[latex]\frac{2}{3}[/latex]
Here n is not an integer.
∴ -150 is not a term of the given A.P.

Question 7.
Find the 31^st term of an A.P. whose 11^th term is 38 and the 16^th term is 73.
Answer:
Given: An A.P. whose

⇒ -5d = -35
⇒ d = [latex]\frac{-35}{-5}[/latex] = 7
Substituting d = 7 in the equation (1)
we get,
a + 10 x 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70 = -32
Now, the 31^st term = a + 30d
= (-32) + 30 × 7
= -32 + 210 = 178

Question 8.
If the 3rd and the 9^th terms of an A.P are 4 and -8 respectively, which term of this A.P is zero?
Answer:
Given: An A.P. whose

Substituting d = -2 in equation (1) we get
a + 2 × (-2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let n^th term of the given A.P be equal to zero.
an = a + (n – 1)d
⇒ 0 = 8 + (n – 1) × (-2)
⇒ 0 = 8 – 2n + 2
⇒ 10 – 2n = 0
⇒ 2n = 10 and n = [latex]\frac{10}{2}[/latex] = 5
∴ The 5^th term of the given A.P is zero.

Question 9.
The 17^th term of an A.P exceeds its 10 term by 7. Find the common difference.
Answer:
Given an A.P in which a₁₇ = a₁₀ + 7
⇒ a₁₇ – a₁₀ = 7
We know that a_n = a + (n – 1)d

⇒ d = [latex]\frac{7}{7}[/latex] = 1

Question 10.
Two APs have the same common difference. The difference between their 100^th terms is 100, what is the difference between their 1000^th terms?
Answer:
Let the first A.P be:
a, a + d, a + 2d, ……..
Second A.P be:
b, b + d, b + 2d, b + 3d, ………
Also, general term, a_n = a + (n – 1)d
Given that, a₁₀₀ – b₁₀₀ = 100
⇒ a + 99d – (b + 99d) = 100
⇒ a – b = 100
Now the difference between their 1000^th terms,

∴ The difference between their 1000^th terms is (a – b) = 100.
Note: If the common difference for any two A.Ps are equal then difference between n^th terms of two A.Ps is same for all natural values of n.

Question 11.
How many three-digit numbers are divisible by 7?
Answer:
The least three digit number is 100.

∴ The least 3 digit number divisible by 7 is 100 + (7 – 2) = 105
The greatest 3 digit number is 999

∴ The greatest 3 digit number divisible by 7 is 999 – 5 = 994.
∴ 3 digit numbers divisible by 7 are
105, 112, 119,….., 994.
a₁ = a = 105; d = 7; a_n = 994
a_n = a + (n – 1)d
⇒ 994 = 105 + (n – 1)7
⇒ (n – 1)7 = 994 – 105
⇒ (n – 1)7 = 889
⇒ n – 1 = [latex]\frac{889}{7}[/latex] = 127
∴ n = 127 + 1 = 128
∴ There are 128, 3 digit numbers which are divisible by 7.
(or)
[latex]\frac{\text { last number – first number }}{7}[/latex]
[latex]\frac{999-100}{7}[/latex]
≃ 128.4 = 128 numbers divisible by 7.

Question 12.
How many multiples of 4 lie between 10 and 250?
Answer:
Given numbers: 10 to 250

∴ Multiples of 4 between 10 and 250 are
First term: 10 + (4 – 2) = 12
Last term: 250 – 2 = 248
∴ 12, 16, 20, 24, ….., 248
a = a₁ = 12; d = 4; a_n = 248
a_n = a + (n – 1)d
248 = 12 + (n – 1) × 4
⇒ (n – 1)4 = 248 – 12
⇒ n – 1 = [latex]\frac{236}{4}[/latex] = 59
∴ n = 59 + 1 = 60
There are 60 numbers between 10 and 250 which are divisible by 4.

Question 13.
For what value of n, are the n^th terms of two APs: 63, 65, 67, ….. and 3, 10, 17,… equal?
Answer:
Given : The first A.P. is 63, 65, 67, ……
where a = 63, d = a₂ – a₁,
⇒ d = 65 – 63 = 2
and the second A.P. is 3, 10, 17, …….
where a = 3; d = a₂ – a₁ = 10 – 3 = 7
Suppose the nth terms of the two A.Ps are equal, where a_n = a + (n – 1)d
⇒ 63 + (n – 1)2 = 3 + (n – 1)7
⇒ 63 + 2n – 2 = 3 + 7n – 7
⇒ 61 + 2n = 7n – 4
⇒ 7n – 2n = 61 + 4
⇒ 5n = 65
⇒ n = [latex]\frac{65}{5}[/latex] = 13
∴ 13^th terms of the two A.Ps are equal.

Question 14.
Determine the AP whose third term is 16 and the 7^th term exceeds the 5^th term by 12.
Answer:
Given : An A.P in which
a₃ = a + 2d = 16 …… (1)
and a₇ = a₅ + 12
i.e., a + 6d = a + 4d + 12
⇒ 6d – 4d = 12
⇒ 2d = 12
⇒ d = [latex]\frac{12}{2}[/latex] = 6
Substituting d = 6 in equation (1) we get
a + 2 × 6 = 16
⇒ a = 16 – 12 = 4
∴ The series/A.P is
a, a + d, a + 2d, a + 3d, …….
⇒ 4, 4 + 6, 4 + 12, 4 + 18, ……
⇒ A.P.: 4, 10, 16, 22, …….

Question 15.
Find the 20^th term from the end of the AP: 3, 8, 13,…, 253.
Answer:
Given: An A.P: 3, 8, 13, …… , 253
Here a = a₁ = 3
d = a₂ – a₁ = 8 – 3 = 5
a_n = 253, where 253 is the last term
a_n = a + (n – l)d
∴ 253 = 3 + (n – 1)5
⇒ 253 = 3 + 5n – 5
⇒ 5n = 253 + 2
⇒ n = [latex]\frac{255}{5}[/latex] = 51
∴ The 20^th term from the other end would be
1 + (51 – 20) = 31 + 1 = 32
∴ a₃₂ = 3 + (32 – 1) × 5
= 3 + 31 × 5
= 3 + 155 = 158

Question 16.
The sum of the 4^th and 8^th terms of an AP is 24 and the sum of the 6^th and 10^th terms is 44. Find the first three terms of the AP.
Answer:
Given an A.P in which a₄ + a₈ = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ……. (1)
and a₆ + a₁₀ = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 ……. (2)
Also a + 5d = 12
⇒ a + 5(5) = 12
⇒ a + 25 = 12
⇒ a = 12 – 25 = -13
∴ The A.P is a, a + d, a + 2d, ……
i.e., – 13, (- 13 + 5), (-13 + 2 × 5)…
⇒ -13, -8, -3, …….

Question 17.
Subba Rao started work in 1995 at an annual salary of Rs. 5000 and received an increment of Rs. 200 each year. In which year did his income reach Rs. 7000?
Answer:
Given: Salary of Subba Rao in 1995 = Rs. 5000
Annual increment = Rs. 200
i.e., His salary increases by Rs. 200 every year.

Clearly 5000, 5200, 5400, forms an A.P in which a = 5000 and d = 200.
Now suppose that his salary reached Rs. 7000 after x – years.
i.e., a_n = 7000
But, a_n = a + (n – 1)d
7000 = 5000 + (n – 1)200
⇒ 7000 – 5000 = (n – 1)200
⇒ n – 1 = [latex]\frac{2000}{200}[/latex] = 10
⇒ n = 10 + 1
∴ In 11^th year his salary reached Rs. 7000.

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.4 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.4

10th Class Maths 6th Lesson Progressions Ex 6.4 Textbook Questions and Answers

Question 1.
In which of the following situations, does the list of numbers involved in the form a G.P.?
i) Salary of Sharmila, when her salary is Rs. 5,00,000 for the first year and expected to receive yearly increase of 10% .
Answer:
Given: Sharmila’s yearly salary = Rs. 5,00,000.
Rate of annual increment = 10 %.

Here, a = a₁ = 5,00,000
a₂ = 5,00,000 × [latex]\frac{11}{10}[/latex] = 5,50,000
a₃ = 5,00,000 × [latex]\frac{11}{10}[/latex] × [latex]\frac{11}{10}[/latex] = 6,05,000
a₄ = 5,00,000 × [latex]\frac{11}{10}[/latex] × [latex]\frac{11}{10}[/latex] × [latex]\frac{11}{10}[/latex] = 6,65,000

Every term starting from the second can be obtained by multiplying its pre¬ceding term by a fixed number [latex]\frac{11}{10}[/latex].
∴ r = common ratio = [latex]\frac{11}{10}[/latex]
Hence the situation forms a G.P.

ii) Number of bricks needed to make each step, if the stair case has total 30 steps. Bottom step needs 100 bricks and each successive step needs 2 bricks less than the previous step.
Answer:
Given: Bricks needed for the bottom step = 100.
Each successive step needs 2 bricks less than the previous step.
∴ Second step from the bottom needs = 100 – 2 = 98 bricks.
Third step from the bottom needs = 98 – 2 = 96 bricks.
Fourth step from the bottom needs = 96 – 2 = 94 bricks.
Here the numbers are 100, 98, 96, 94, ….
Clearly this is an A.P. but not G.P.

iii) Perimeter of the each triangle, when the mid-points of sides of an equilateral triangle whose side is 24 cm are joined to form another triangle, whose mid-points in turn are joined to form still another triangle and the process continues indefinitely.

Answer:
Given: An equilateral triangle whose perimeter = 24 cm.
Side of the equilateral triangle = [latex]\frac{24}{3}[/latex] = 8 cm.
[∵ All sides of equilateral are equal] ……. (1)
Now each side of the triangle formed by joining the mid-points of the above triangle in step (1) = [latex]\frac{8}{2}[/latex] = 4 cm
[∵ A line joining the mid-points of any two sides of a triangle is equal to half the third side.]
Similarly, the side of third triangle = [latex]\frac{4}{2}[/latex] = 2 cm
∴ The sides of the triangles so formed are 8 cm, 4 cm, 2 cm,
a = 8

Thus each term starting from the second; can be obtained by multiplying its preceding term by a fixed number [latex]\frac{1}{2}[/latex].
∴ The situation forms a G.P.

Question 2.
Write three terms of the G.P. when the first term ‘a’ and the common ratio ‘r’ are given.
i) a = 4 ; r = 3.
Answer:
The terms are a, ar, ar², ar³, ……..
∴ 4, 4 × 3, 4 × 3² , 4 × 3² , ……
⇒ 4, 12, 36, 108, ……

ii) a = √5 ; r = [latex]\frac{1}{5}[/latex]
Answer:
The terms are a, ar, ar², ar³, ……..

iii) a = 81 ; r = -[latex]\frac{1}{3}[/latex]
Answer:
The terms of a G.P are:
a, ar, ar², ar³, ……..

⇒ 81, -27, 9,

iv) a = [latex]\frac{1}{64}[/latex]; r = 2.
Answer:
Given: a = [latex]\frac{1}{64}[/latex]; r = 2.

∴ The G.P is [latex]\frac{1}{64}[/latex], [latex]\frac{1}{32}[/latex], [latex]\frac{1}{16}[/latex], …….

Question 3.
Which of the following are G.P. ? If they are G.P, write three more terms,
i) 4, 8, 16, ……
Answer:
Given: 4, 8, 16, ……
where, a₁ = 4; a₂ = 8; a₃ = 16, ……
[latex]\frac{a_{2}}{a_{1}}=\frac{8}{4}=2[/latex]
[latex]\frac{a_{3}}{a_{2}}=\frac{16}{8}=2[/latex]
∴ r = [latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}[/latex] = 2
Hence 4, 8, 16, … is a G.P.
where a = 4 and r = 2
a₄ = a . r³ = 4 × 2³ = 4 × 8 = 32
a₅ = a . r⁴ = 4 × 2⁴ = 4 × 16 = 64
a₆ = a . r⁵ = 4 × 2⁵ = 4 × 32 = 128

ii) [latex]\frac{1}{3}[/latex], -[latex]\frac{1}{6}[/latex], [latex]\frac{1}{12}[/latex], …….
Answer:
Given: t₁ = [latex]\frac{1}{3}[/latex], t₂ = -[latex]\frac{1}{6}[/latex], t₃ = [latex]\frac{1}{12}[/latex], ….
[latex]\frac{1}{3}[/latex], -[latex]\frac{1}{6}[/latex], [latex]\frac{1}{12}[/latex], …….

Hence the ratio is common between any two successive terms.
∴ [latex]\frac{1}{3}[/latex], -[latex]\frac{1}{6}[/latex], [latex]\frac{1}{12}[/latex], ……. is G.P.
where a = [latex]\frac{1}{3}[/latex] and r = -[latex]\frac{1}{2}[/latex]

iii) 5, 55, 555, ……..
Answer:
Given: t₁ = 5, t₂ = 55, t₃ = 555, ….

∴ 5, 55, 555, …….. is not a G.P.

iv) -2, -6, -18, ……
Given: t₁ = -2, t₂ = -6, t₃ = -18

∴ -2, -6, -18, is a G.P.
where a = -2 and r = 3
a_n = a . r^n-1 =
a₄ = a . r³ = (-2) × 3³ = -2 × 27 = -54
a₅ = a . r⁴ = (-2) × 3⁴ = -2 × 81 = -162
a₆ = a . r⁵ = (-2) × 3⁵ = -2 × 243 = -486

v) [latex]\frac{1}{2}[/latex], [latex]\frac{1}{4}[/latex], [latex]\frac{1}{6}[/latex], …….
Answer:

i.e., [latex]\frac{1}{2}[/latex], [latex]\frac{1}{4}[/latex], [latex]\frac{1}{6}[/latex], ….. is not a G.P.

vi) 3, -3², 3³, ……
Given: t₁ = 3, t₂ = -3², t₃ = 3³, ……


i.e., every term is obtained by multiplying its preceding term by a fixed number -3.
3, -3², 3³, …… forms a G.P,
where a = 3; r = -3
a_n = a . r^n-1
a₄ = a . r³ = 3 × (-3)³ = 3 × (-27) = -81
a₅ = a . r⁴ = 3 × (-3)⁴ = 3 × 81 = 243
a₆ = a . r⁵ = 3 × (-3)⁵ = 3 × (-243) = -729

vii) x, 1, [latex]\frac{1}{x}[/latex], …….
Answer:
Given: t₁ = x, t₂ = 1, t₃ = [latex]\frac{1}{x}[/latex], ……

Hence x, 1, [latex]\frac{1}{x}[/latex], …. forms a G.P.
where a = x; r = [latex]\frac{1}{x}[/latex]

viii) [latex]\frac{1}{\sqrt{2}}[/latex], -2, [latex]\frac{8}{\sqrt{2}}[/latex], …….
Answer:
Given: t₁ = [latex]\frac{1}{\sqrt{2}}[/latex], t₂ = -2, t₃ = [latex]\frac{8}{\sqrt{2}}[/latex], ……

ix) 0.4, 0.04, 0.004, ……..
Answer:
Given: t₁ = 0.4, t₂ = 0.04, t₃ = 0.004, ……

∴ 0.4, 0.04, 0.004, …….. forms a G.P.
where a = 0.4; r = [latex]\frac{1}{10}[/latex]

Question 4.
Find x so that x, x + 2, x + 6 are consecutive terms of a geometric progression.
Answer:
Given x, x + 2 and x + 6 are in G.P. but read it as x, x + 2 and x + 6.
∴ r = [latex]\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}[/latex] = [latex]\frac{\mathrm{t}_{3}}{\mathrm{t}_{2}}[/latex]
⇒ [latex]\frac{x+2}{x}[/latex] = [latex]\frac{x+6}{x+2}[/latex]
⇒(x + 2)² = x(x + 6)
⇒ x² + 4x + 4 = x² + 6x
⇒ 4x – 6x = – 4 = -2x = -4
∴ x = 2

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry Ex 7.1 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry Exercise 7.1

10th Class Maths 7th Lesson Coordinate Geometry Ex 7.1 Textbook Questions and Answers

Question 1.
Find the distance between the following pair of points,
(i) (2, 3) and (4, 1)
Answer:
Distance = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]
= [latex]\sqrt{(4-2)^{2}+(1-3)^{2}}[/latex]
= [latex]\sqrt{4+4}[/latex]
= √8 = 2√2 units

ii) (- 5, 7) and (-1, 3)
Answer:
Distance = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]
= [latex]\sqrt{(-1+5)^{2}+(3-7)^{2}}[/latex]
= [latex]\sqrt{4^{2}+(-4)^{2}}[/latex]
= [latex]\sqrt{16+16}[/latex]
= √32 = 4√2 units

iii) (- 2, -3) and (3, 2)
Answer:

iv) (a, b) and (- a, – b)
Answer:

Question 2.
Find the distance between the points (0, 0) and (36, 15).
Answer:
Given: Origin O (0, 0) and a point P (36, 15).
Distance between any point and origin = [latex]\sqrt{x^{2}+y^{2}}[/latex]
∴ Distance = [latex]\sqrt{36^{2}+15^{2}}[/latex]
= [latex]\sqrt{1296+225}[/latex]
= [latex]\sqrt{1521}[/latex]
= 39 units

∴ 1521 = 3² × 13²
[latex]\sqrt{1521}[/latex] = 3 × 13 = 39

Question 3.
Verify that the points (1, 5), (2, 3) and (-2, -1) are collinear or not.
Answer:
Given: A (1, 5), B (2, 3) and C (- 2, – 1)

Here the sum of no two segments is equal to third segment.
Hence the points are not collinear.
!! Slope of AB, m₁ = [latex]\frac{3-5}{2-1}[/latex] = -2
Slope of BC, m₂ = [latex]\frac{-1-3}{-2-2}[/latex] = 1
m₁ ≠ m₂
Hence A, B, C are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7,-2) are the vertices of an isosceles triangle.
Answer:
Let A = (5, – 2); B = (6, 4) and C = (7, – 2).

Now we have, AB = BC.
∴ △ABC is an isosceles triangle,
i.e., given points are the vertices of an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in figure. Jarina and Phani walk into the class and after observing for a few minutes Jarina asks Phani “Don’t you think ABCD is a square?” Phani disagrees. Using distance formula, find which of them is correct. Why?

Answer:
Given: Four friends are seated at A, B, C and D where A (3, 4), B (6, 7), C (9, 4) and D (6, 1).
Now distance

BD = [latex]\sqrt{(6-6)^{2}+(1-7)^{2}}[/latex] = √36 = 6
Hence in □ ABCD four sides are equal
i.e., AB = BC = CD = DA
= 3√2 units
and two diagonals are equal.
i.e., AC = BD = 6 units.
∴ □ ABCD forms a square.
i.e., Jarina is correct.

Question 6.
Show that the following points form an equilateral triangle A(a, 0), B(- a, 0), C(0, a√3).
Answer:
Given: A (a, 0), B (- a, 0), C (0, a√3).

Now, AB = BC = CA.
∴ △ABC is an equilateral triangle.

Question 7.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram.
Answer:
To show that the given points form a parallelogram.
We have to show that the mid points of each diagonal are same. Since diagonals of a parallelogram bisect each other.
Now let A(-7, -3), B(5, 10), C(15, 8) and D(3, -5)
Then midpoint of diagonal

∴ (1) = (2)
Hence the given are vertices of a parallelogram.

Question 8.
Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of a rhombus. And find its area.
(Hint: Area of rhombus = [latex]\frac{1}{2}[/latex] × product of its diagonals)
Answer:
Given in ▱ ABCD , A(-4, – 7), B (- 1, 2), C (8, 5) and D (5,-4)


∴  In ▱ ABCD, AB = BC = CD = AD [from sides are equal]
Hence ▱ ABCD is a rhombus.
Area of a rhombus = [latex]\frac{1}{2}[/latex] d₁d₂
= [latex]\frac{1}{2}[/latex] × 12√2 × 6√2
= 72 sq. units.

Question 9.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
i) (-1,-2), (1,0), (-1,2), (-3,0)
Answer:
Let A (- 1, -2), B (1, 0), C (- 1, 2), D (- 3, 0) be the given points. Distance formula

In ▱ ABCD, AB = BC = CD = AD – four sides are equal.
AC = BD – diagonals are equal.
Hence, the given points form a square,

ii) (-3, 5), (1, 10), (3, 1), (-1,-4).
Answer:
Let A(-3, 5), B(l,10), C(3, 1), D(-l, -4) then

In ▱ ABCD, [latex]\overline{\mathrm{AB}}[/latex] = [latex]\overline{\mathrm{CD}}[/latex] and [latex]\overline{\mathrm{BC}}[/latex] = [latex]\overline{\mathrm{AD}}[/latex] (i.e., both pairs of opposite sides are equal) and [latex]\overline{\mathrm{AC}}[/latex] ≠ [latex]\overline{\mathrm{BD}}[/latex].
Hence ▱ ABCD is a parallelogram,
i.e., The given points form a parallelogram.

iii) (4, 5), (7, 6), (4, 3), (1, 2).
Answer:
Let A (4, 5), B (7, 6), C (4, 3) and D (1, 2) be the given points.
Distance formula

In ▱ ABCD, AB = CD and BC = AD (i.e., both pairs of opposite sides are equal) and AC ≠ BD.
Hence ▱ ABCD is a parallelogram, i.e., The given points form a parallelogram.

Question 10.
Find the point on the X-axis which is equidistant from (2, -5) and (-2,9).
Answer:
Given points, A (2, – 5), B (- 2, 9).
Let P (x, 0) be the point on X – axis which is equidistant from A and B. i.e., PA = PB.
Distance formula = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]

But PA = PB.
⇒ [latex]\sqrt{x^{2}-4 x+29}=\sqrt{x^{2}+4 x+85}[/latex]
Squaring on both sides, we get
x² – 4x + 29 = x² + 4x + 85
⇒ – 4x – 4x = 85 – 29
⇒ – 8x = 56
⇒ x = [latex]\frac{56}{-8}[/latex] = -7
∴ (x, 0) = (- 7, 0) is the point which is equidistant from the given points.

Question 11.
If the distance between two points (x, 7) and (1, 15) is 10, find the value of x.
Answer:
Formula for distance between two points = [latex]\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}[/latex]
Now distance between (x, 7) and (1,15) is 10.
∴ [latex]\sqrt{(x-1)^{2}+(7-15)^{2}}[/latex] = 10
∴ (x – l)² + (-8)² = 10²
⇒ (x – l)² = 100 – 64 = 36
∴ x – 1 = √36 = ± 6
∴ x – 1 = 6 or x – 1 = -6
⇒ x = 6 + 1 = 7 or x = -6 + 1 = -5
∴ x = 7 or x = – 5

Question 12.
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Answer:
Given: P (2, – 3), Q (10, y) and
[latex]\overline{\mathrm{PQ}}[/latex] = 10.
Distance formula = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]

⇒ y² + 6y + 73 = 100
⇒ y² + 6y – 27 = 0
⇒ y² + 9y – 3y – 27 = 0
⇒ y (y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = -9 or y = 3
⇒ y = – 9 or 3.

Question 13.
Find the radius of the circle whose centre is (3, 2) and passes through (-5,6).
Answer:

Given: A circle with centre A (3, 2) passing through B (- 5, 6).
Radius = AB
[∵ Distance of a point from the centre of the circle]
Distance formula = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]

Question 14.
Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14)? Give reason.
Answer:
Let A (1, 5), B (5, 8) and C (13, 14) be the given points.
Distance formula

Here, AC = AB + BC.
∴ △ABC can’t be formed with the given vertices.
[∵ Sum of the any two sides of a triangle must be greater than the third side].

Question 15.
Find a relation between x and y such that the point (x, y) is equidistant from the points (-2, 8) and (-3, -5).
Answer:
Let A (- 2, 8), B (- 3, – 5) and P (x, y). If P is equidistant from A, B, then PA = PB.
Distance formula =


Squaring on both sides we get, x² + y² + 4x – 16y + 68
= x² + y² + 6x +10y + 34
⇒ 4x – 16y – 6x – 10y = 34-68
⇒ – 2x – 26y = -34
⇒ x + 13y = 17 is the required condition.