Mahesh

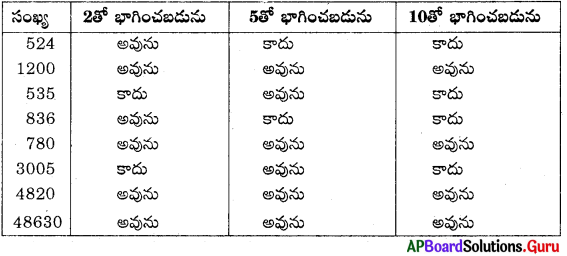
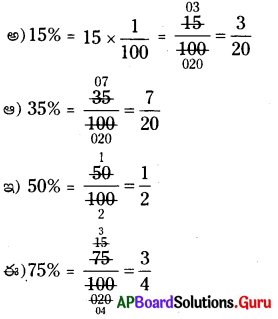
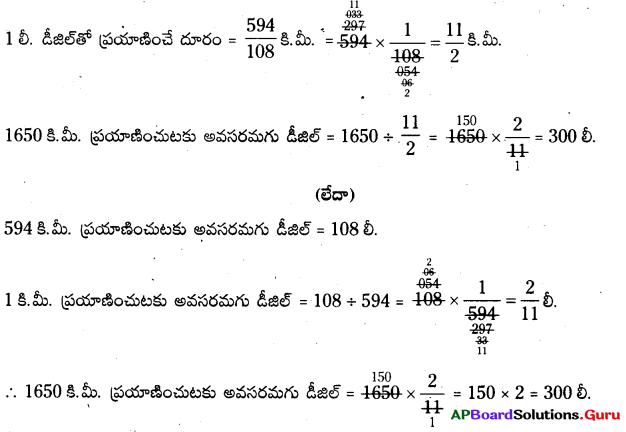
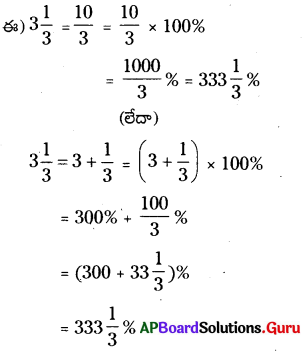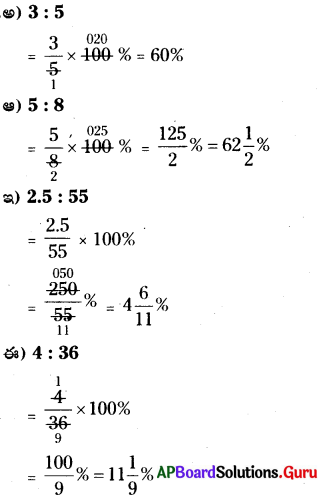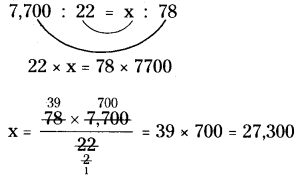Practice the AP 7th Class Science Bits with Answers Chapter 4 Respiration and Circulation on a regular basis so that you can attempt exams with utmost confidence.

AP 7th Class Science Bits Chapter 4 Respiration and Circulation with Answers

I. Multiple Choice Questions

1. In which process accumulated semisolid wastes come out?
A) Sneezing
B) Yawning
C) Coughing
D) Apnea
Answer:
C) Coughing

2. Which of the following is occured when food enters in the wind pipe?
A) Sneezing
B) Yawning
C) Coughing
D) Apnea
Answer:
D) Apnea

3. First aid for bleeding is
A) Create pressure on the diaphragm
B) Cover with bandage
C) Upside down
D) Above all
Answer:
B) Cover with bandage

4. Which of the following requires oxygen?
A) Aerobic respiration
B) Anaerobic respiration
C) Both A & B
D) None
Answer:
A) Aerobic respiration

5. The process of inhaling air is called
A) Breathing
B) Inspiration
C) Expiration
D) Respiration
Answer:
B) Inspiration

6. The opening of the nose is called
A) Nostrils
B) Nasal cavity
C) Pharynx
D) wind pipe
Answer:
A) Nostrils

7. Inspiration occurs due to
A) Ribcage move upward
B) Diaphragm move upward
C) Air enters the lungs
D) A & B
Answer:
A) Ribcage move upward

8. Quantity of nitrogen present in the inhaled air …………%.
A) 21
B) 25
C) 78
D) 0.4
Answer:
C) 78

9. Quantity of water vapour in exhaled air 0.4 …………%.
A) 15
B) 4
C) 78
D) 3
Answer:
D) 3

10. This gas turns lime water into milky white
A) Oxygen
B) Hydrogen
C) Carbon dioxide
D) Nitrogen
Answer:
C) Carbon dioxide

11. Find the correct statement
i) In the lungs, Carbon dioxide from the inhaled air is absorbed by the blood vessels present in the lungs.
ii) Oxygen collected by the blood vessels from all parts of the body enters into the Lungs.
A) both are correct
B) i only correct
C) ii only correct
D) both are wrong
Answer:
D) both are wrong

12. This will help to quit smoking.
A) Will power
B) support of the family and friends
C) medical and psychological treatment
D) All the above
Answer:
D) All the above

13. Nicotine is present in this leaf
A) Neem
B) Pipal
C) Tobacco
D) Betel
Answer:
C) Tobacco

14. Find the odd one
A) Grasshopper
B) Cockroach
C) Earthworm
D) Honey bee
Answer:
C) Earthworm

15. Frogs respires through
A) Lungs
B) Skin
C) Tracheae
D) Both A & B
Answer:
D) Both A & B

16. Fish respire through
A) Gills
B) Skin
C) Lung
D) Both A & B
Answer:
A) Gills

17. Marine animal that respire through lung is
A) Fish
B) Dolphins
C) Prawn
D) Star fish
Answer:
B) Dolphins

18. Respiration in plants occurs through
A) Stomata
B) Lenticles
C) Root hairs
D) All the above
Answer:
D) All the above

19. Honey bee : Tracheae :: Earth worm : ?
A) Gill
B) Lung
C) Skin
D) None of, these
Answer:
C) Skin

20. In this process, energy released in our body
A) Photosynthesis
B) Digestion
C) Respiration
D) Circulation
Answer:
C) Respiration

21. This process helps in the supply of digested food and oxygen to all parts of the body
A) Digestion
B) Circulation
C) Excretion
D) Photosynthesis
Answer:
B) Circulation

22. This is not a part of circulatory system ….
A) Lungs
B) Heart
C) Blood vessels
D) Blood
Answer:
A) Lungs

23. Upper two chambers of the heart are called
A) Arteries
B) Ventricles
C) Atria
D) Veins
Answer:
C) Atria

24. The fluid portion of the blood is
A) RBC
B) WBC
C) Blood platelets
D) Plasma
Answer:
D) Plasma

25. They protect us from the harmful, disease causing micro organisms that enter into our body.
A) RBC
B) WBC
C) Blood platelets
D) Plasma
Answer:
B) WBC

26. They play an important role in coagulation of blood…….
A) RBC
B) WBC
C) Blood platelets
D) Plasma
Answer:
C) Blood platelets

27. They plays a key role in respiration.
A) RBC
B) WBC
C) Blood platelets
D) Plasma
Answer:
A) RBC

28. Which of the following does not have blue coloured blood
A) Prawns
B) Snails
C) Cockroach
D) Crabs
Answer:
D) Crabs

29. This life processes play an important role in release of energy in organisms.
A) Digestion
B) Respiration
C) Circulation
D) All the above
Answer:
A) Digestion

30. Which of the following is not a non communicable diseases?
A) Heart attack
B) COVID – 19
C) Cancer
D) Paralysis
Answer:
B) COVID – 19

31. Identify the bacterial disease
A) Common cold
B) Polio
C) Tuberculosis
D) HIV
Answer:
C) Tuberculosis

32. Identify the viral, disease
A) Typhoid
B) Common cold
C) Cholera
D) Tuberculosis
Answer:
B) Common cold

33. SMS protocol is for this disease
A) Polio
B) COVID
C) Cancer
D) Paralysis
Answer:
B) COVID

34. This is caused due to insufficient supply of Oxygen to the brain.
A) Coughing
B) Sneezing
C) Deglutition
D) Yawning
Answer:
D) Yawning

35. This process prevents the food from entering into the windpipe.
A) Coughing
B) Sneezing
C) Deglutition
D) Yawning
Answer:
C) Deglutition

36. This occurs when the wind pipe is obstructed by an object leading to blocking of air….
A) Coughing
B) Sneezing
C) Deglutition
D) Choking
Answer:
D) Choking

II. Fill in the blanks

1. COVID -19 is caused by a virus called …………………… .
2. SARS means …………………… .
3. Giving assistance before a doctor attending is called …………………… .
4. The temporary arrest of respiration is called …………………… .
5. The process of inhalation and exhalation of air is called …………………… .
6. The process of inhaling air is called …………………… .
7. The process of exhalation of air is called …………………… .
8; The number of times we inhale and exhale air in a minute is called the
9. We breathe about …………………… times per minute normally.
10. One inhalation and one exhalation together called one
11. …………………… is the first part of the Wind pipe.
12. …………………… is the process which helps in the release of energy in our body.
13. …………………… are the respiratory organs in human beings.
14. The …………………… lung is slightly larger than the …………………… one.
15. Wind pipe is kept in its shape by …………………… .
16. Lungs are protected by …………………… .
17. …………………… is the thin muscular sheet attached to the lower side of the ribcage.
18. …………………… forms the floor of the chest cavity.
19. …………………… play key role in the respiratory movements in man.
20. …………………… play key role in the respiratory movements in woman.
21. …………………… are the only part of the human body which floats on water
22. …………………… is the gas produced in photosynthesis.
23. Percentage of carbon dioxide in the inhaled air is …………………… .
24. Percentage of oxygen in the inhaled air is …………………… .
25. Percentage of carbon dioxide in the exhaled air is …………………… .
26. Percentage of oxygen in the exhaled air is …………………… .
27. Lime water turns milky white when it reacts with …………………… .
28. Glucose + Oxygen → …………………… + water + Energy
29. Tobacco smoke contains a highly dangerous substance called
30. …………………… respiration is present in insects.
31. Breathing through the skin is called …………………… respiration.
32. Respiration carried out by gills is called …………………… .
33. Respiration through is called Pulmonary respiration.
34. Plants respire through on the leaf and on the stem.
35. …………………… is the pumping organ in the blood circulatory system.
36. Upper two chambers of the heart are called and lower two chambers are called …………………… .
37. The rhythmic contraction followed by its relaxation of the heart is called …………………… .
38. Heart beat can be felt and measured by an instrument called …………………… .
39. …………………… carry blood with more oxygen from heart to body parts.
40. …………………… carry blood with more carbon dioxide from the body parts to the heart.
41. …………………… connect the arteries with the Veins
42. …………………… is the fluid portion of the blood.
43. …………………… act like police force of our body.
44. Red blood cells have a colouring pigment called …………………… .
45. …………………… acts as a carrier for oxygen and carbon dioxide in blood.
46. …………………… play an important role in coagulation of blood …………………… .
47. Blood present in cockroach is
48. …………………… is the storage point for undigested food.
49. Blood in snails is …………………… in colour.
50. …………………… was the new disease that created a global impact recently.
51. …………………… is the inbuilt capacity of the body to fight and overcome the effects of disease-causing germs.
52. The entry of disease-causing germs into our body is called ……………… .
53. COVID-19 virus spreads primarily through …………………… of infected person.
Answer:

1. SARS CoV – 2
2. Severe Acute Respiratory Syndrome
3. First aid.
4. Apnea
5. breathing
6. inspiration
7. expiration
8. Respiratory Rate
9. 14 to 20
10. breath
11. Larynx
12. Respiration
13. Lungs
14. right
15. C Shaped rings
16. ribcage
17. Diaphragm
18. Diaphragm
19. Diaphragm
20. Ribcage
21. Lungs
22. Oxygen
23. 0.04%
24. 21%
25. 4%
26. 15%
27. carbon dioxide
28. Carbon dioxide
29. Nicotine
30. Tracheal
31. cutaneous
32. branchial respiration
33. lungs
34. stomata, lenticels
35. Heart
36. atria, ventricles
37. heartbeat
38. Stethoscope
39. Arteries
40. Veins
41. Blood capillaries
42. Plasma
43. White blood cells
44. Haemoglobin
45. Haemoglobin
46. Blood platelets
47. colourless
48. Rectum
49. bluish
50. COVID-19
51. Immunity
52. infection
53. droplets of saliva or nasal discharges

III. Match the following

1.

Group – A	Group – B
A) Opening of the nose	1) Nostrils
B) Mucus and nasal hair	2) Nasal cavity
C) Common chamber	3) Lungs
D) Wide tube	4) Wind pipe
E) Branches of wind pipe	5) Bronchi
F) Spongy and elastic	6) Pharynx

Answer:

Group – A	Group – B
A) Opening of the nose	1) Nostrils
B) Mucus and nasal hair	2) Nasal cavity
C) Common chamber	6) Pharynx
D) Wide tube	5) Bronchi
E) Branches of wind pipe	4) Wind pipe
F) Spongy and elastic	3) Lungs

2.

Group – A	Group – B
A) Red blood cells	1) Earthworm
B) White blood cells	2) Cockroach
C) Blood platelets	3) Carrier for oxygen and carbondioxide
D) Colourless blood	4) Coagulation of blood
E) Blue colour blood	5) Police force of our body
	6) Snails

Answer:

Group – A	Group – B
A) Red blood cells	3) Carrier for oxygen and carbondioxide
B) White blood cells	5) Police force of our body
C) Blood platelets	4) Coagulation of blood
D) Colourless blood	2) Cockroach
E) Blue colour blood	6) Snails

3.

Group – A	Group – B
A) Sneezing	1) Wastes in the lungs expelled out
B) Yawning	2) Inhale air with dust
C) Coughing	3) Obstruction Of wind pipe leading to blocking Of air
D) Apnea	4) Bleeding injury
E) Choking	5) Insufficient supply of Oxygen to the brain
	6) Prevents the food from, entering into the windpipe

Answer:

Group – A	Group – B
A) Sneezing	2) Inhale air with dust
B) Yawning	5) Insufficient supply of Oxygen to the brain
C) Coughing	1) Wastes in the lungs expelled out
D) Apnea	6) Prevents the food from, entering into the windpipe
E) Choking	3) Obstruction Of wind pipe leading to blocking Of air

4.

Group – A	Group – B
A) Typhoid	1) Non communicable diseases
B) Polio	2) Pumping organ in the circulatory system
C) Heart attack	3) Bacterial disease
D) Capillaries	4) Carry blood with more oxygen
E) Heart	5) Viral disease

Answer:

Group – A	Group – B
A) Typhoid	3) Bacterial disease
B) Polio	5) Viral disease
C) Heart attack	1) Non communicable diseases
D) Capillaries	6) Connect the arteries with the veins
E) Heart	2) Pumping organ in the circulatory system

Practice the AP 7th Class Science Bits with Answers Chapter 3 Nutrition in Organisms on a regular basis so that you can attempt exams with utmost confidence.

AP 7th Class Science Bits Chapter 3 Nutrition in Organisms with Answers

I. Multiple Choice Questions

1. Carbohydrates digest first in
A) Buccal cavity
B) Stomach
C) Small intestine
D) Large intestine
Answer:
A) Buccal cavity

2. Proteins digestion starts in
A) Buccal cavity
B) Stomach
C) Small intestine
D) Large intestine
Answer:
B) Stomach

3. Chocolates, sweets, soft drinks and other sugar products cause of
A) Acidity
B) Constipation
C) Tooth decay
D) Diarrhea
Answer:
C) Tooth decay

4. The process of intake and utilization of food by organisms is called ……
A) Digestion
B) Absorption
C) Nutrition
D) Excretion
Answer:
C) Nutrition

5. Nutrition in green plants is
A) Autotrophic
B) Saprophytic
C) Parasitic
D) Holozoic
Answer:
A) Autotrophic

6. This is not a requirement of photosynthesis
A) Oxygen
B) Carbon dioxide
C) light
D) water
Answer:
A) Oxygen

7. Product of photosynthesis
A) Oxygen
B) Water
C) Glucose
D) All the above
Answer:
D) All the above

8. Presence of starch in leaves indicates the occurrence of…..
A) Respiration
B) Photosynthesis
C) Digestion
D) Excreton
Answer:
B) Photosynthesis

9. This works as food factory of the plant
A) Stem
B) Leaf
C)Flower
D) Root
Answer:
B) Leaf

10. Function of stomata is
A) Gaseous exchange
B) Transport of water
C) Food production
D) Digestion
Answer:
A) Gaseous exchange

11. Find the correct statement
i) Nepenthes is a insectivorous plant.
ii) It grow in phosphorous deficient soils.
A) both are correct
B) i only correct
C) ii only correct
D) both are wrong
Answer:
B) i only correct

12. Example for saprophyte
A) Amoeba
B) Utricularia
C) Cuscuta
D) Bread mould
Answer:
D) Bread mould

13. Chlorophyll-containing partner in the lichens is
A) Algae
B) Fungi
C) Bacteria
D) Amoeba
Answer:
A) Algae

14. Cuscuta absorbs its food from host through
A) Tap root
B) Fibrous root
C) Haustoria
D) prop roots
Answer:
C) Haustoria

15. National Deworming Day is observed on
A) February 10
B) August 10
C) Both A & B
D) December 10
Answer:
C) Both A & B

16. Albendazole tablet is a…
A) Antibiotic
B) Antiviral drug
C) Antifungal drug
D) Deworming drug
Answer:
D) Deworming drug

17. Taking of food into the body is called…..
A) Ingestion
B) Digestion
C) Absorption
D) Egestion
Answer:
A) Ingestion

18. Conversion of food into simple soluble forms is called …
A) Ingestion
B) Digestion
C) Absorption
D) Egestion
Answer:
B) Digestion

19. Transfer of food to the blood is called …..
A) Ingestion
B) Digestion
C) Absorption
D) Egestion
Answer:
C) Absorption

20. Removal of waste products and undigested food from the body
A) Ingestion
B) Digestion
C) Absorption
D) Egestion
Answer:
D) Egestion

21. Amoeba collects its food with the help of
A) Pseudopodia
B) Nucleolus
C) Food vacuole
D) Cytoplasm
Answer:
A) Pseudopodia

22. This is not digestible in human being is …..
A) Starch
B) Protein
C) Fat
D) Cellulose
Answer:
D) Cellulose

23. Nutrition in human being is …
A) Autotrophic
B) Parasitic
C) Saprophytic
D) Holozoic
Answer:
D) Holozoic

24. The total length of alimentary canal is about
A) 3 meters
B) 6 meters
C) 9 meters
D) 12 meters
Answer:
C) 9 meters

25. Tofal number of teeth in the adult is
A) 8
B) 16
C) 20
D) 32
Answer:
D) 32

26. Teeth that help to cut the food….
A) incisors
B) canines
C) premolars
D) molars
Answer:
A) incisors

27. Hardest part of the human body is
A) Bone
B) Teeth
C) Cartilage
D) Muscle
Answer:
B) Teeth

28. The major culprits of tooth decay ….
A) Chocolates
B) Sweets
C) Soft drinks
D) All the above
Answer:
D) All the above

29. Common chamber for both digestive track and respiratory track is
A) Pharynx
B) Duodenum
C) Esophagus
D) Buccal cavity
Answer:
A) Pharynx

30. The muscular tubular structure that connects pharynx with Stomach is
A) Buccal cavity
B) Oesophagus
C) Duodenum
D) Small intestine
Answer:
B) Oesophagus

31. Hydrochloricacid in the stomach kills Bacteria in the food.
A) Lactic acid
B) Sulphuric acid
C) Acetic acid
D) Hydrochloric acid
Answer:
D) Hydrochloric acid

32. Digestion of food completes in this part
A) Stomach
B) Duodenum
C) Small intestine
D) Large intestine
Answer:
C) Small intestine

33. Digested food absorbed in to blood through
A) Stomach
B) Duodenum
C) Villi
D) Large intestine
Answer:
C) Villi

34. Large intestine absorbs….
A) Water
B) Digested food
C) Minerals
D) A & C
Answer:
D) A & C

35. Reason for acidity…
A) Stress
B) Irregular meals
C) Drinking too much alcohol
D) All the above
Answer:
D) All the above

36. The only asana that can be done on full stomach.
A) Padmaasan
B) Vajrasana
C) Bhujangasana
D) shirshaasana
Answer:
B) Vajrasana

II. Fill in the blanks

1. Liver produces …………… juice.
2. Expand NDD ……………
3.
4. The process of intake and utilization of food by organisms is called …………… .
5. The mqde of nutrition in which organisms make food by themselves is called …………… .
6. The mode of nutrition in which organisms depend on other organisms, for food is called …………… .
7. Green plants are …………… .
8. Humans and animals are directly or indirectly dependent on …………… for food.
9. …………… are the special structures present only in plant cells and absent in animal cells.
10. Chlorophyll is present in the …………… of plant cell.
11. …………… is the pigment responsible for the greenery of the plants.
12. The process-by which green plants make their own food from carbon dioxide and water by using light energy in the presence of chlorophyll is called …………… .
13. Glucose formed in photosynthesis is converted and stored in the form of …………… .
14. The presence of starch in leaves indicates the occurrence of …………… .
15. Occurrence of photosynthesis can be confirmed by testing the leaf extract with …………… solution.
16. …………… work as “food factories of plants”.
17. …………… captures the energy of the sunlight.
18. …………… is the source of energy in the process of photosynthesis.
19. …………… is the ultimate source of energy for all living organisms.
20. Gaseous exchange occurs in the leaves through …………… .
21. …………… is the gas required for photosynthesis.
22. …………… is the gas produced in photosynthesis.
23. Nutrients needed ip minute quantities are called …………… .
24. Insectivorous plants meet their requirements from insects.
25. Saprophytes grow on …………… .
26. The mode of nutrition in which organisms take in nutrients in the form of solution from dead and decaying matter is called …………… nutrition.
27. …………… play key role in cleaning,up the earth surface.
28. Chlorophyll-containing partner in lichen is
29. An association between two organisms for food in which one organism get benefited and other is vitiated is called ……………
30. The organism that get benefited in parasitism is …………… .
31. Organism on which parasite is growing is called …………… .
32. …………… is the mode of heterotrophic nutrition in which the food is taken in solid or liquid form from the outside and is digested inside the body.
33. Pseudopodia are food collecting, organs in …………… .
34. Humans cannot digest …………… .
35. The digestive system consists Of the …………… and …………… .
36. The total length Of alimentary canal is about …………… meters.
37. Teeth in the human beings are of …………… types.
38. …………… is the hardest part of the human body.
39. …………… is the only asana that can be done on full stomach.
40. Damage of teeth due to acids is called …………… .
41. Carbohydrate digestion starts in …………… .
42. …………… is the common chamber for both digestive track and respiratory track.
43. Proteins digestions starts in the …………… .
44. …………… in the stomach kills Bacteria in the food.
45. Inner wall of the small intestine have thousands of finger-like outgrowths called …………… .
46. Villi absorb the …………… .
47 …………… absorbs water and minerals from the undigested food.
48. …………… is the storage;point for undigested food.
49. Fecal matter removed through …………… .
Answer:

1. bile
2. National Deworming Day
3. carbondioxide, oxygen
4. nutrition
5. autotrophic nutrition
6. heterotrophic nutrition
7. autotrophs
8. plants
9. Chloroplasts
10. chloroplast
11. Chlorophyll
12. Photosynthesis
13. starch.
14. photosynthesis
15. Iodine
16. Leaves
17. Chlorophyll
18. Sunlight
19. Sun
20. stomata.
21. Carbon dioxide
22. Oxygen
23. micronutrients
24. nitrogen
25. dead and decaying matter
26. saprophytic
27. Saprophytes
28. algae
29. parasitism.
30. parasite
31. host
32. Holozofc Nutrition
33. amoeba
34. cellulose
35. Tooth
36. Vajrasana
37. tooth decay
38. buccal cavity
39. Pharynx
40. stomach
41. Hydrochloric acid
42. villi.
43. digested food
44. Large Intestine
45. Rectum
46. anus.

III. Match the following

1.

Group – A	Group – B
A) Ingestion	1) Transfer of food to the blood.
B) Digestion	2) Absorbed food became the part of the body
C) Absorption	3) Preparing food inside the body
D) Assimilation	4) Removal of undigested food from the body.
E) Egestion	5) Conversion of food into simple soluble forms.
	6) Food is taken into the body.

Answer:

Group – A	Group – B
A) Ingestion	6) Food is taken into the body.
B) Digestion	5) Conversion of food into simple soluble forms.
C) Absorption	3) Preparing food inside the body
D) Assimilation	2) Absorbed food became the part of the body
E) Egestion	4) Removal of undigested food from the body.

2.

Group – A	Group – B
A) Autotrophs	1) Mouth
B) Saprophytes	2) Special roots
C) Parasite	3) Chlorophyll
D) Holozoic	4) Solution

Answer:

Group – A	Group – B
A) Autotrophs	3) Chlorophyll
B) Saprophytes	4) Solution
C) Parasite	2) Special roots
D) Holozoic	1) Mouth

3.

Group – A	Group – B
A) Buccal cavity	1) Removes fecal matter
B) Stomach	2) Absorbs water and minerals
C) Small intestine	3) Starts carbohydrate digestion
D) Large intestine	4) Preparing food inside the body.
E) Anus	5) Starts protein digestion
	6) Complete the digestion of food

Answer:

Group – A	Group – B
A) Buccal cavity	3) Starts carbohydrate digestion
B) Stomach	5) Starts protein digestion
C) Small intestine	6) Complete the digestion of food
D) Large intestine	2) Absorbs water and minerals
E) Anus	1) Removes fecal matter

4.

Group – A	Group – B
A) Utricularia	1) Ruminants
B) Venus fly trap	2) Others
C) Cuscuta	3) Bladderwort
D) Cows	4) Nourishment
E) Trophos	5) Dionaea
	6) Dodder plant

Answer:

Group – A	Group – B
A) Utricularia	3) Bladderwort
B) Venus fly trap	5) Dionaea
C) Cuscuta	6) Dodder plant
D) Cows	1) Ruminants
E) Trophos	4) Nourishment

Practice the AP 7th Class Science Bits with Answers Chapter 2 Nature of Substances on a regular basis so that you can attempt exams with utmost confidence.

AP 7th Class Science Bits Chapter 2 Nature of Substances with Answers

I. Multiple Choice Questions

1. Table salt contains
A) Sodium chloride
B) Sodium bicarbonate
C) Potassium chloride
D) Sodium hydroxide
Answer:
A) Sodium chloride

2. Baking soda contains
A) Sodium chloride
B) Sodium bicarbonate
C) Potassium chloride
D) Sodium hydroxide
Answer:
B) Sodium bicarbonate

3. Gastric juice means
A) Sulphuric acid
B) Citric acid
C) Antacid
D) Hydrochloric acid
Answer:
D) Hydrochloric acid

4. Sulphuric acid reacts with eggshell and releases
A) Carbondioxide
B) Hydrogen
C) Oxygen
D) None
Answer:
A) Carbondioxide

5. Substance/s formed in a neutralization reaction is/are
A) Water
B) Salt
C) A and B
D) Hydrogen
Answer:
C) A and B

6. Which of the following does not contain acid?
A) lemon
B) Bitter gourd
C) Amla
D) Tomato
Answer:
B) Bitter gourd

7. This acid is present in cool drinks
A) Sulphuric acid
B) Hydrochloric acid
C) Carbonic acid
D) Vinegar
Answer:
C) Carbonic acid

8. Bath soap is prepared using
A) Sodium hydroxide
B) Aluminum hydroxide
C) Calcium carbonate
D) Potassium hydroxide
Answer:
D) Potassium hydroxide

9. Olfactory indicator from the following
A) Hibiscus
B) Phenolphthalein
C) Clove oil
D) Methyl orange
Answer:
C) Clove oil

10. lichens are used in the preparation of
A) Litmus
B) Methyl blue
C) Phenolphthalein
D) Olfactory indicators
Answer:
A) Litmus

11. Phenolphthalein shows colour change with
A) Acids
B) Bases
C) both A & B
D) Neutral substances
Answer:
B) Bases

12. Which of the following is a strong acid?
A) Citric acid
B) Acetic acid
C) Sulphuric acid
D) Malic acid
Answer:
C) Sulphuric acid

13. This gas is lighter than air
A) Hydrogen
B) Nitrogen
C) Oxygen
D) Carbon dioxide
Answer:
A) Hydrogen

14. Product of neutralisation
A) Salt
B) Water
C) Both A & B
D) Acid
Answer:
C) Both A & B

15. Example for salt
A) Common salt
B) Antacid
C) Tooth paste
D) Clove oil
Answer:
A) Common salt

16. Acid produced in stomach
A) Sulphuric acid
B) Hydrochloric acid
C) Nitric acid
D) Carbonic acid
Answer:
B) Hydrochloric acid

17. This can be used to treat ant bite
A) Baking soda
B) Common salt
C) Vinegar
D) Turmeric
Answer:
A) Baking soda

18. pH of bases
A) 0-14
B) 7
C) more than 7
D) less than 7
Answer:
C) more than 7

19. This is responsible for acid rains
A) Sulphur dioxide
B) Nitrogen dioxide
C) Both A & B
D) Oxygen
Answer:
C) Both A & B

20. Flowers that change their colour according to the nature of soil
A) Hydrangea
B) Marigold
C) Hibiscus
D) Jasmine
Answer:
A) Hydrangea

II. Fill in the blanks.

1. Rain with slight ………….. nature is called acid rains.
2. Wash the affected burning area on skin with ………….. .
3. ………….. will be prepared by adding fatty acids to alkalis.
4. ………….. are used in making soaps.
5. ………….. are used to test the nature of substances.
6. ………….. acid is also called as Vitamin C.
7. ………….. acid is used for bath room cleaning.
8. ………….. acid is used in batteries.
9. Soda water and cool drinks contain ………….. acids.
10. Bases are ………….. to taste.
11. Bath soap is prepared using ………….. .
12. Detergent soap is prepared using
13. Bases that can dissolve in water are called ………….. .
14. The substance which is neither an acid nor a base is known as ………….. .
15. Purewater is a ………….. substance.
16. Substances which are used to test acids or bases are called ………….. .
17. Indicators obtained from natural sources are called as ………….. .
18. The most commonly used natural indicator is ………….. .
19. The colour of turmeric strip will change into ………….. in soap water.
20. Soda water turns into ………….. on adding hibiscus indicator.
21. Soap solutions turns ………….. on adding hibiscus indicator.
22. An indicator prepared from artificialsources is known as ………….. .
23. Methyl orange turns in acids and ………….. in bases.
24. Phenolphthalein turns ………….. in bases, but ………….. in acids.
25. Substances which change their smell when mixed with acid or base are known as ………….. .
26. ………….. is a mixture of different indicators and shows different colours in different solutions.
27. ………….. can show the strength of acid or alkaline substance.
28. Strength of acid or base solution is measured in ………….. scale.
29. pH of acids is ………….. .
30. pH of bases is ………….. .
31. pH of neutral substance is ………….. .
32. Natural acids are ………….. acids.
33. Acids react with metals and release gas.
34. Acids react with ………….. and release carbon dioxide gas.
35. Reaction of an acid and a base is called ………….. reaction.
36. The substances formed in neutralization reaction are ………….. and ………….. .
37. Antacids contain ………….. .
38. When an ant bites, it injects acid into the skin.
39. When soil becomes too acidic, farmers treat it by adding
40. When soil becomes too basic,farmers treat it with
41. Rain water with slight acidic nature is called
42. ………….. acid is used in the preservation of pickles and other food substances.
43. ………….. acid is used in the production of ink and leather.
44. Base used in windows cleaner is ………….. .
45. Magnesium hydroxide is used in ………….. and ………….. .
Answer:

1. acidic
2. plenty of water
3. Soap
4. Bases
5. Indicators
6. Ascorbic
7. Hydrochloric
8. Sulphuric
9. carbonic
10. bitter
11. potassium hydroxide
12. Sodium hydroxide
13. alkalis
14. neutral substance
15. Neutral
16. acid base indicators
17. Natural indicators.
18. litmus
19. reddish brown
20. pink
21. green
22. Synthetic indicator.
23. red, yellow
24. pink, does not change
25. olfactoryin dicators.
26. Universal indicatoris
27.  Universal indicator
28. pH
29. less than 7
30. more than 7
31. 7
32. weak
33. hydrogengas.
34. calcium carbonate
35. neutralization reaction.
36. water, salt
37. bases.
38. formic
39. quick lime/ potassium hydroxide.
40. compost.
41. Acid rain.
42. Acetic
43. Tannic
44. Ammonium hydroxide
45. antacid and laxative

III. Match the following

1.

Group – A	Group – B
A) Blue litmus in acid	1) Yellow
B) Methyl orange in base	2) No change
C) Hibiscus in acid	3) Red
D) Phenolphthalein in acid	4) Brown
E) Turmeric in base

Answer:

Group – A	Group – B
A) Blue litmus in acid	3) Red
B) Methyl orange in base	1) Yellow
C) Hibiscus in acid	5) Pink
D) Phenolphthalein in acid	2) No change
E) Turmeric in base	4) Brown

2.

Group – A	Group – B
A) Hydrangea plants	1) Air pollution
B) Neem	2) pH of the soil
C) pH scale	3) Chew sticks
D) Nitric acid	4) Manufacture of fertilizers
E) Acid rain	5) Automobile battery
	6) Sorensen

Answer:

Group – A	Group – B
A) Hydrangea plants	2) pH of the soil
B) Neem	3) Chew sticks
C) pH scale	6) Sorensen
D) Nitric acid	4) Manufacture of fertilizers
E) Acid rain	1) Air pollution

3.

Group – A	Group – B
A) Antacid	1) Formic acid
B) Ant	2) Salt and water
C) Neutralisation	3) Bases that can dissolve in water
D) Olfactory indicator	4) Stomach
E) Alkalis	5) Hibiscus
	6) Clove oil

Answer:

Group – A	Group – B
A) Antacid	4) Stomach
B) Ant	1) Formic acid
C) Neutralisation	2) Salt and water
D) Olfactory indicator	6) Clove oil
E) Alkalis	3) Bases that can dissolve in water

Practice the AP 7th Class Science Bits with Answers Chapter 1 Food for Health on a regular basis so that you can attempt exams with utmost confidence.

AP 7th Class Science Bits Chapter 1 Food for Health with Answers

I. Multiple Choice Questions

1. Which of the following is good for health?
A) Sprouts
B) Packaged cool drinks
C) Junk foods
D) Above all
Answer:
A) Sprouts

2. Chikki (Chickpea) contains
A) Proteins
B) Iron
C) Calcium
D) Above all
Answer:
D) Above all

3. Street food have
A) rich in fibre
B) rich in fat
C) rich in minerals
D) above all
Answer:
B) rich in fat

4. Which water is better to drink?
A) Packaged drinking water
B) Tap water
C) Boiled water
D) Above all
Answer:
C) Boiled water

5. Ascorbic acid is called as
A) Vitamin A
B) Vitamin C
C) Vitamin K
D) Vitamin E
Answer:
B) Vitamin C

6. This gives instant energy to the body.
A) Chicken
B) Egg
C) Glucose
D) Ghee
Answer:
C) Glucose

7. Which of the following is the main source of energy for our body?
A) carbohydrates
B) proteins
C) fats
D) vitamins
Answer:
A) carbohydrates

8. Identify the energy giving food.
A) carbohydrates
B) proteins
C) fats
D) A & C
Answer:
D) A & C

9. Identify the food item rich in carbohydrates.
A) Pulses
B) Groundnut
C) Potato
D) Almond
Answer:
C) Potato

10. Reagent used to test the presence of starch
A) Benedict’s reagent
B) Iodine
C) Copper sulphate solution
D) All the above
Answer:
B) Iodine

11. Starch turn in to this colour when it come in contact with iodine solution
A) Blue black
B) Violet
C) Pink
D) Reddish green
Answer:
A) Blue black

12. Which of the following food sample gives blue black colour with iodine solution?
A) Jowar
B) Rice
C) Maize
D) All the above
Answer:
D) All the above

13. Reagent used to test the presence of sugar
A) Benedict’s reagent
B) Iodine
C) Copper sulphate solution
D) Sodium hydroxide solution
Answer:
A) Benedict’s reagent

14. Which of the following are called body building nutrients?
A) carbohydrates
B) proteins
C) fats
D) A & C
Answer:
B) proteins

15. Identify the functions of proteins from the following.
A) Helps in the formation of muscles and other body organs.
B) Regulate biochemical reactions in the body.
C) Repair and heal the wounds on the body.
D) All the above
Answer:
D) All the above

16. Find the odd one out.
A) Meet
B) Maize
C) Egg
D) Soya been
Answer:
B) Maize

17. Animal source of protein ….
A) Milk
B) Fish
C) Pulses
D) A & B
Answer:
D) A & B

18. What colour change will you observe when egg white reacts with 2% copper sulphate and 10% sodium hydroxide solutions
A) White to blue black
B) White to violet
C) White to pink
D) White to reddish green
Answer:
B) White to violet

19. Which of the following gives more energy when they are taken in equal quantities?
A) carbohydrates
B) proteins
C) fats
D) vitamins
Answer:
C) fats

20. Groundnuts paste turns white paper in to
A) Transparent
B) Translucent
C) Opaque
D) Violet colour
Answer:
B) Translucent

21. What tablets will you suggest to an anaemia patient?
A) Calcium
B) Iron
C) Vitamin D
D) Phosphorus
Answer:
B) Iron

22. Minerals and vitamins are called
A) Energy giving nutrients
B) Body building nutrients
C) Protective nutrients
D) Anutritive components
Answer:
C) Protective nutrients

23. Mineral element responsible for strong bones and teeth
A) Calcium
B) Iron
C) Phosphorus
D) A & C
Answer:
D) A & C

24. Mineral element responsible for blood production and transfer of oxygen
A) Calcium
B) Iron
C) Phosphorus
D) Sodium
Answer:
B) Iron

25. Deficiency of this mineral causes Goitre disease.
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
C) Iodine

26. Milk, curd are rich in
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
A) Calcium

27. This mineral helps in retaining the water needed for our body.
A) Calcium
B) Iron
C) Phosphorus
D) Sodium
Answer:
D) Sodium

28. Common salt is the major source for
A) Calcium
B) Sodium
C) Phosphorus
D) Iron
Answer:
B) Sodium

29. Iodized salt helps in preventing
A) Anaemia
B) Goitre
C) Night blindness
D) Scurvy
Answer:
B) Goitre

30. Which of the following is not a fat-soluble vitamin?
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
B) Vitamin – B

31. Which of the following is a water-soluble vitamin?
A) Vitamin – A
B) Vitamin – K
C) Vitamin – E
D) Vitamin – C
Answer:
D) Vitamin – C

32. Deficiency of vitamin – A causes
A) Dry Eyes
B) Night blindness
C) Cornea failure
D) All the above
Answer:
D) All the above

33. Which of the following is not a deficiency disease of vitamin – B complex?
A) Beri-Beri
B) Scurvy
C) Fits
D) Pellagra
Answer:
B) Scurvy

34. Deficiency of vitamin – D causes
A) Rickets
B) Scurvy
C) Night blindness
D) Fertility disorders
Answer:
A) Rickets

35. Scurvy caused due to the deficiency of
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

36. Fertility disorders may be due to the deficiency of
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
D) Vitamin – E

37. Somu is suffering from delay in blood clotting during injuries. What might be the reason?
A) Vitamin – A deficiency
B) Vitamin – K deficiency
C) Vitamin – D deficiency
D) Vitamin – E deficiency
Answer:
B) Vitamin – K deficiency

38. This vitamin is responsible for health of the bone and teeth.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
D) Vitamin – D

39. Function of vitamin A
A) Health of Nerves
B) Formation of RBC
C) Health of Bone and teeth
D) Health of eye, hair and skin
Answer:
D) Health of eye, hair and skin

40. This vitamin is responsible for the health of gums.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

41. Vitamin – E is responsible for
A) Health of Nerves
B) Formation of RBC
C) Health of Bone and teeth
D) Health of eye, hair and skin
Answer:
A) Health of Nerves

42. Citrus fruits are the rich source of this vitamin.
A) Vitamin – C
B) Vitamin – B
C) Vitamin – A
D) Vitamin – K
Answer:
A) Vitamin – C

43. Sunlight is required to form this vitamin in our body.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
C) Vitamin – D

44. Eating carrots can prevent
A) Rickets
B) Scurvy
C) Night blindness
D) Fertility disorders
Answer:
C) Night blindness

45. This vitamin plays an important role in increasing immunity.
A) Vitamin – A
B) Vitamin – C
C) Vitamin – D
D) Vitamin – K
Answer:
B) Vitamin – C

46. Which vitamin discolourises the iodine paper?
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

47. Dietary fibres prevent
A) Rickets
B) Scurvy
C) Night blindness
D) Constipation
Answer:
D) Constipation

48. Anutritive component of our food is
A) carbohydrates
B) proteins
C) fats
D) water
Answer:
D) water

49. Weight of the water in our body is nearly
A) 2/3 of our body weight
B) 3/2 of our body weight
C) 1/5 of our body weight
D) 14 of our body weight
Answer:
A) 2/3 of our body weight

50. Function of water in our body
A) Maintains the temperature of our body
B) Helps in excretion of wastes
C) Helps in easy movement of the food in digestive track
D) All the above
Answer:
D) All the above

51. Irregular bowel movements refer to
A) Rickets
B) Constipation
C) Night blindness
D) Scurvy
Answer:
B) Constipation

52. This may be the cause for constipation
A) poor diet with insufficient fibre
B) poor fluid intake
C) side effect of certain medication blindness
D) all the above
Answer:
D) all the above

53. Food component present more in Black gram
A) carbohydrates
B) proteins
C) fats
D) all the above
Answer:
B) proteins

54. Jaggery is a rich source of
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
B) Iron

55. National Institute of Nutrition (NIN) is located at
A) Delhi
B) Mumbai
C) Pune
D) Hyderabad
Answer:
D) Hyderabad

56. Inadequate proteins in children’s diet for a long-time cause
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
C) Kwashiorkor

57. Inadequate carbohydrates and proteins in children’s diet for a long-time cause
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
A) Marasmus

58. Taking food containing too much fat leads to
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
D) Obesity

59. Which of the following should be taken more in our diet?
A) Cereals
B) Pulses
C) Vegetables
D) Obesity
Answer:
C) Vegetables

60. Which of the following should be taken in very less quantity in our diet?
A) Cereals
B) pulses
C) Vegetables
D) Oils
Answer:
D) Oils

61. How much quantity of milk /curd should be taken every day?
A) 300 ml
B) 100 ml
C) 500 ml
D) 1000 ml
Answer:
A) 300 ml

62. Grains like bajra and ragi are rich in
A) Calcium
B) iron
C) Both A&B
D) Calcium
Answer:
C) Both A&B

63. Which of the following is not a C from the 7 C’s prescribed by FSSAI?
A) Check
B) Clean
C) Control
D) Cover
Answer:
C) Control

II. Fill in the blanks.

1. Eating junk food on a regular basis damages our ………….. system.
2. Grains like bajra and ragi are rich in ………….. and ………….. .
3. Packaged cold drinks contain high amounts of ………….., which is bad for the teeth and bones.
4. Drinking of tea/ coffee less than one hour before and after eating food impairs the absorption of ………….. in the body.
5. Jaggery is a good source of ………….. .
6. Carbohydrates, proteins and fats are required in ………….. quantity. Hence, they are called ………….. .
7. Minerals and Vitamins are required in very ………….. quantity. So, they are called ………….. .
8. Carbohydrates and fats mainly provide ………….. to our body.
9. Sports persons take glucose as it gives ………….. .
10. Carbohydrates are usually present in the form of ………….. and ………….. in the food.
11. Presence of starch is confirmed by doing test.
12. Starch turns into in colour when it come in contact with Iodine solution.
13. ………….. test confirms the presence of sugars.
14. ………….. are needed for the growth and maintenance of our body.
15. ………….. are called body building nutrients.
16. repair and heal the wounds on the body.
17. Proteins turn into ………….. colour when they react with 2% copper sulphate solution and 10% sodium hydroxide solution.
18. Pulses are rich in ………….. .
19. ………….. give more energy when compared to the same amount of carbohydrates.
20. Fats turn the white paper ………….. .
21. ………….. and ………….. help in protecting our body against diseases.
22. ………….. and ………….. are required for strong bones and teeth.
23. ………….. is the mineral responsible for blood production and transfer of oxygen.
24. ………….. is the mineral required for the thyroid hormone secretions.
25. Sea foods are rich source of ………….. .
26. ………….. is the mineral that helps to retain water needed for the body.
27. Weekly Iron Folic Acid Supplementation Scheme was launched to prevent
28. Vitamins – A, D, E, K are ………….. soluble Vitamins.
29. Vitamins – C, B complex are ………….. soluble Vitamins.
30. Health of eye, hair and skin is maintained by the vitamin ………….. .
31. Dry eyes is caused due to the deficiency of the vitamin ………….. .
32. Pellagra is caused due to the deficiency of the vitamin ………….. .
33. Health of skin, teeth, gums and blood cells is maintained by the vitamin ………….. .
34. Eating Citrus fruits can prevent the diseases ………….. .
35. Sun light is required to form the vitamin in our body.
36. ………….. is the disease caused due to the deficiency of vitamin D.
37. Vitamin E is responsible for the health of ………….. .
38. Deficiency of Vitamin E causes ………….. .
39. Vitamin ………….. helps in the clotting of blood when we get wounded.
40. Vitamin ………….. plays an important role in increasing disease resistant or immunity.
41. ………….. paper gets discoloured with vitamin C.
42. The substances which made the iodine paper more discoloured contains more vitamin ………….. .
43. ………….. help in free bowel movement in the digestive tract and prevent the constipation.
44. Water constitutes nearly ………….. of our body weight.
45. ………….. refers to bowel movements that are irregular.
46. A diet that contains all the nutrients in required quantity is called ………….. .
47. NIN is located at ………….. .
48. According to ‘My plate for the day’ by NIN quantity of nuts and seeds recommended is ………….. .
49. Diseases caused by deficiency of certain nutrients are called ………….. .
50. Healthy eating habits and also play a key role in maintaining of health.
51. If the proteins are inadequate in children’s diet for a long time it causes ………….. .
52. If the proteins and carbohydrates are not taken adequately for a long time it causes ………….. .
53. If we take food containing too much fats daily, it leads to ………….. .
Answer:

1. digestive
2. Calcium and iron
3. acid
4. iron
5. iron
6. More, Macro nutrients
7. Less micro nutrients
8. energy
9. instant energy
10. Starch and sugars
11. iodine
12. black blue
13. Benedict’s reagent
14. Proteins
15. Proteins
16. Proteins
17. violet
18. Proteins
19. fat
20. translucent
21. Minerals and Vitamins
22. Calcium and Phosphate
23. Iron
24. Iodine
25. Iodine
26. Sodium
27. Anemia
28. Fat
29. water
30. A
31. A
32. B
33. C
34. scurvy
35. D
36. rickets
37. nerves and blood cells
38. Fertility disorders
39. K
40. C
41. iodine
42. C
43. Dietary fibres / roughage
44. 2/3
45. Constipation
46. balanced diet
47. Hyderabad
48. 30 gms/day
49. Deficiency diseases
50. hygiene
51. Kwashiorkor
52. Marasmus
53. obesity

III. Match the following

1.

Group – A	Group – B
A) Vitamin A	1) rickets
B) Vitamin B	2) scurvy
C) Vitamin C	3) delay in clotting of blood
D) Vitamin D	4) beri beri
E) Vitamin K	5) dry eyes

Answer:

Group – A	Group – B
A) Vitamin A	5) dry eyes
B) Vitamin B	4) beri beri
C) Vitamin C	2) scurvy
D) Vitamin D	1) rickets
E) Vitamin K	3) delay in clotting of blood

2.

Group – A	Group – B
A) Micro-nutrient	1) Calcium
B) Strong bones and teeth	2) Iodine
C) Goitre	3) Sodium
D) Retains water in body	4) Carbohydrate
E) Macro-nutrient	5) Vitamins
	6) Iron

Answer:

Group – A	Group – B
A) Micro-nutrient	5) Vitamins
B) Strong bones and teeth	1) Calcium
C) Goitre	2) Iodine
D) Retains water in body	3) Sodium
E) Macro-nutrient	4) Carbohydrate

3.

Group – A	Group – B
A) Scurvy	1) B complex vitamin
B) Fertility disorders	2) Vitamin K
C) Rickets	3) Vitamin C
D) Delay in clotting of blood	4) Vitamin D
E) Beri Beri	5) Vitamin E
	6) Vitamin A

Answer:

Group – A	Group – B
A) Scurvy	3) Vitamin C
B) Fertility disorders	5) Vitamin E
C) Rickets	4) Vitamin D
D) Delay in clotting of blood	2) Vitamin K
E) Beri Beri	1) B complex vitamin

4.

Group – A	Group – B
A) Citrus fruits	1) Calcium
B) Jaggery	2) Iodine
C) Sea foods	3) Proteins
D) Potato	4) Carbohydrate
E) Egg white	5) Vitamin C
	6) Iron

Answer:

Group – A	Group – B
A) Citrus fruits	5) Vitamin C
B) Jaggery	6) Iron
C) Sea foods	2) Iodine
D) Potato	4) Carbohydrate
E) Egg white	3) Proteins