Mahesh

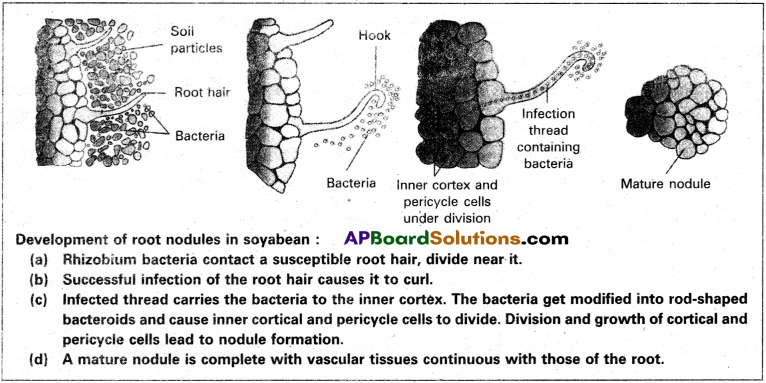
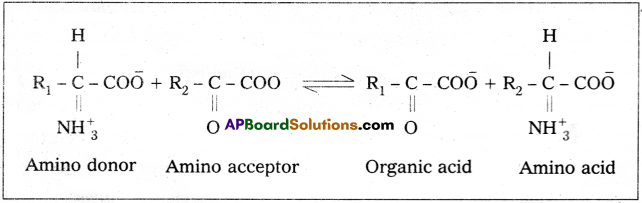
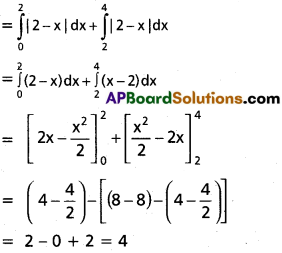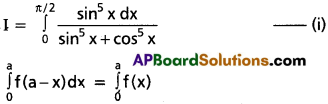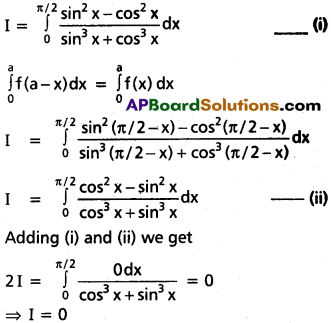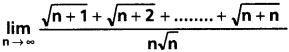Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 3rd Lesson Enzymes Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 3rd Lesson Enzymes

Very Short Answer Questions

Question 1.
How are prosthetic groups different from co-factors?
Answer:
Prosthetic groups are organic compounds that are tightly bound to the apoenzyme (protein part of the enzyme) whereas cofactors are non-protein parts of the holoenzyme.

Question 2.
What is meant by feedback inhibition?
Answer:
The end product of a chain of enzyme-catalyzed reactions inhibits the enzyme of the first reaction as a part of homostatic control of metabolism is called feedback inhibition.

Question 3.
W hy are ‘oxido reductases’ so named?
Answer:
Enzyme which catalyse oxidation and reduction of substrates usually involving hydrogen transfer are called oxido reductases.

Question 4.
Distinguish between apoenzyme and cofactor.
Answer:
The protein part of a holoenzyme is called apoenzyme the non-protein part of a holoenzyme is called cofactor.

Question 5.
What are competitive enzyme inhibitors? Mention one example.
Answer:
Substances which are closely resembles the substrate molecules and inhibits the activity of the enzyme are called competitive inhibitors.
Eg : Inhibition of succinic dehydrogenase by malonate which closely resembles the substrate succinate.

Question 6.
What are non-competitive enzyme inhibitors? Mention one example.
Answer:
The inhibitor has no structural similarity with the substrate and bind to an enzyme of locations other than the active sites so that the globular structure of the enzyme is changed are called non-Competitive enzyme inhibitors.
Eg : Metal ions of Copper, Mercury.

Question 7.
What do the four digits of an enzyme code indicate?
Answer:
In enzyme code, the first digit indicates the major class of the enzyme the second digit and the third digit indicate sub class and sub-sub class respectively. The last digit of the code is the serial number of the enzyme.

Question 8.
Who proposed ‘Lock and Key hypotheses’ and ‘Induced fit hypothesis’?
Answer:
Lock and key hypothesis was proposed by Emil Fisher (1884). Induced fit hypothesis was proposed by Daniel E. Koshland (1973).

Question 9.
Define Michael’s constant?
Answer:
Substrate cencentration required to cause half the maximal reaction rate is termed as michalis menten constant (km).

Short Answer Questions

Question 1.
Write briefly about enzyme inhibitors.
Answer:
The chemicals that can shut off enzyme activity are called inhibitors. They are of 3 types.
1) Competitive inhibitors:
Substances which closely resemble the substrate molecules and inhibits the activity of the enzyme are called competitive inhibitors.
Eg : Inhibition of succinic dehydrogenase by malonate which closely resembles the substrate succinate.

2) Non-competitive inhibitors :
The inhibitors which have no structural similarity with the substrate and bind to an enzyme at locations other than the active sites, so that the globular structure of the enzyme is changed are called non competitive inhibitors.
Eg: Metal ions of Copper, Mercury.

3) Feedback inhibitors :
The end product of a chain of enzyme catalysed reactions inhibit the enzyme of the first reaction as a part of homoeostatic control of metabolism are called feed back inhibitors.
Eg : During respiration (Glycolysis) accumalation of Glucose-6 Phosphate occurs, it inhibits the Hexokinase.

Question 2.
Explain different types of co-factors.
Answer:
Cofactors are two types.
1) Metal ion cofactor :
Metallic cations get tightly attached to the apoenzyme are called metallo enzymes.
Eg : Cu⁺² cytochrome oxidase

2) Organic cofactors :
They are two types.
a) Coenzyme :
They are small organic molecules which are loosely associated with the apoenzyme.
Eg : Thiamine pyrophosphate, Vitamin B.

b) Prosthetic group :
They are the organic cofactors which are tightly bounded to the apoenzyme.
Eg : Haeme is the prosthetic group of enzyme peroxidase.

Question 3.
Explain the mechanism of enzyme action.
Answer:
The substrate ‘S’ has to bind the enzyme of its active site with in a given cleft. The substrate has to diffuse towards the active site leads to the formation of ES complex. This is called transition state structure. Very Soon, after the expected bond breaking /making is completed, the product is released from the active site. In other words, the structure of substrate gets transformed into the structure of products.

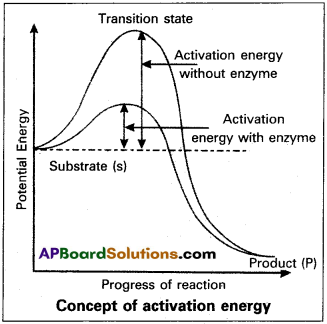
When we represent this pictorially through a graph by taking potential energy on y-axis and progress of reaction on x-axis, we notice the energy level difference between ‘S’ and ‘P’. If ‘P’ is at lower level than S, it is an exothermic reaction. One need flot supply energy to form the product. However, whether it is an exothermic or an endothermic reaction (Energy requiring reaction) the ‘S’ has to go through a much higher energy state or transition state.

The difference between average energy content of ‘S’ and that of this transition state is called activation energy. –

Each enzyme [E] has a substrate [S] binding site in its molecule so that a highly reactive enzyme substrate complex [ES] is produced. This complex is short lived and dissociates into its products [P] and the unchanged enzyme with an intermediate formation of the enzyme product complex [EP].
E+S → ES → EP → E+P

Formation of ES complex has been explained with lock and key hypothesis by Emil Fisher and much later with induced fit hypothesis by Daniel E. Koshland.
The catalytic cycle of an enzyme action ‘is

1. The substrate binds to the active site of the enzyme.
2. The binding of the substrate induces the enzyme to alter its shape, fitting more tightly around the substrate.
3. The active site of the enzyme breaks the chemical bonds of the substrate and the new enzyme product complex is formed.
4. The enzyme releases the products of the reaction and the free enzyme is ready to bind to another molecule of the substrate.

Intext Questions

Question 1.
Explain how pH effects enzyme activity with the help of a graphical representation.
Answer:

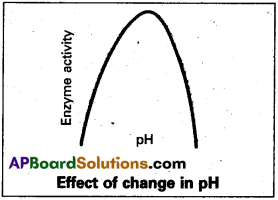
Enzymes generally function in a narrow range of pH. Each enzyme shows its highest activity at a particular pH called optimum pH.
Activity declines both below and above the optimum level.

Question 2.
Explain the importance of [ES] complex formation.
Answer:
Each enzyme [E] has a substrate [S] binding site in its molecule so that a highly reactive enzyme substrate complex [ES] is produced. This complex is short lived and dissociates into its products [P] and the unchanged enzyme with an intermediate formation of the enzyme product complex [EP].
E+S → ES → EP → E+P

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 2nd Lesson Mineral Nutrition Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 2nd Lesson Mineral Nutrition

Very Short Answer Questions

Question 1.
Define hydroponics.
Answer:
The technique of growing plants in a specified nutrient solution in the complete absence of soil is known as hydroponics.

Question 2.
How do you categorize a particularly essential element as a macro or micronutrient?
Answer:
The elements which are present in large amounts i.e., in excess of 10m mole kg^-1 of dry matter are called Macronutrients. The elements which are needed in small amounts i.e., less than 10m mole kg^-1 of dry matter are called micronutrients.

Question 3.
Give two examples of essential elements that act as activators for enzymes.
Answer:
Molebdinum, Magnesium and Zn⁺².

Question 4.
Name the. essential mineral element that play an important role in photolysis of water.
Answer:
Calcium and Manganese.

Question 5.
Out of the 17 essential elements, which elements are called non-mineral essential elements?
Answer:
Carbon, Oxygen, Hydrogen and Nitrogen.

Question 6.
Name two amino acids in which sulphur is present.
Answer:
Cysteine and Methionine.

Question 7.
When is an essential element said to be deficient?
Answer:
The element said to be deficient when present below the critical concentration [The Cone, of the essential elements below which plant growth is retarded is termed as critical concentration].

Question 8.
Name two elements whose symptoms of deficiency first appear in younger leaves.
Answer:
Sulphur and Calcium.

Question 9.
Explain the role of the pink colour pigment in the root nodule of legume plants. What is it called?
Answer:
The enzyme nitrogenase is highly sensitive to the molecular oxygen. It is protected from oxygen by pink colour pigment cailed an oxygen scavenger, leg haemoglobin.

Question 10.
Which element is regarded as the 17^th essential element? Name the disease caused by its deficiency.
Answer:
Nickel. It’s deficiency cause Mouse ear in pecan. [Slightly wrinkled leaves round or blunt leaflets].

Question 11.
Name the essential elements present in nitrogenase enzyme. What type of essential elements are they?
Answer:
Nitrogenase enzyme contains Mo and Fe elements. They are Micronutrients.

Question 12.
Write the balanced equation of nitrogen fixation.
Answer:
N₂ + 8H⁺ + 8e^– + 16 ATP → 2NH₃ + H₂ + 16ADP + 16 Pi

Question 13.
Name any two essential elements and the deficiency diseases caused by them.
Answer:
Chlorosis occurs due to the deficiency of N, K, Mg, S, Fe, Mn, Zn and Mo.
Neurosis occurs due to the deficiency of Ca, Mg, Cu, K.

Short Answer Questions

Question 1.
Explain the steps involved in the formation of root nodule.
Answer:

1. Roots of legumes release sugars, amino acids which attracted Rhizobium. They get attached to epidermal and root hair cells of the host.
2. The root hair curl and the bacteria invade the root hair.
3. An infection thread is produced, carrying the bacteria into cortex of the root.
4. Bacteria initiate nodule formation in the cortex of the root. Then the bacteria released from the thread into the cortical cells of the host and stimulate the host cells to divide. Thus leads to the differentiation of specialized nitrogen fixing cells.
5. The nodule thus formed establishes a direct vascular connection with the host for exchange of nutrients.

Question 2.
Write in brief, how plants synthesize amino acids.
Answer:
Amino acids are synthesized into two ways. They are
1) Reductive Amination :
In this ammonia reacts with a-ketoglutaric acid and forms glutamic acid.

2) Transamination :
In this, transfer of an amino group from an amino acid to the keto group of a keto acid. Glutamic acid is the main amino acid from which the transfer of NH₂ takes place and other amino acids are formed in the presence of transaminase.

Question 3.
Explain in brief, how plants absorb essential elements.
Answer:
The process of absorption can be demarcated into two main phases. In the 1^st phase, there is an initial uptake of ions into the free space or outer space of cells – the apoplast. It is a passive process. In the second phase of uptake, the ions are taken in slowly into the inner space – the symplast.

The passive movement of ions into the apoplast from the cell along the concentration gradient usually occurs through ion-channels. The entry or exit of ions to and from the symplast against the concentration gradient requires metabolic energy which is an active process.

Question 4.
Explain the Nitrogen cycle, giving relevant examples.
Answer:
The cyclic movement of nitrogen from the atmosphere to soil and from soil back into the atmosphere through plants, animals and micro-organisms is termed as nitrogen cycle. Nitrogen cycle is a continuous pathway and it involves five steps.

1. Nitrogen Fixation
2. Nitrogen Assimilation
3. Ammonification
4. Nitrification
5. Denitrification

1) Nitrogen Fixation :
The gaseous dinitrogen is fixed into inorganic nitrogenous substances is called nitrogen fixation. It occurs by two methods.
a) Abiological or physical method,
b) Biological method – Dia2otrophy.

a) Abiological or physical method :

1. It occurs in atmosphere. Due to thunders and lightening, dinitrogen is converted into nitric acid which is further oxidised to nitrogen dioxide.
2. These oxides dissolves in rain water and reaches soil as nitrous and nitric acids.
3. These acids react with alkali radicles of soil and form nitrates.
4. The soluble nitrates are directly absorbed by plants. The reactions of physical nitrogen fixation are as follows.
   1) N₂ + O₂ → 2NO
   2) 2NO + O₂ → 2NO₂
   3) 2NO₂ + H₂O → HNO₂ + HNO₃
   4) HNO₃ + Ca or K salts → Ca or K nitrates.
   5) A biological nitrogen fixation is carried put on industrial scale by Haber Bosch process at 0°C with 1000°C bars pressure.

b) Biological method – Diazotrophy :
1) Conversion of dinitrogen into nitrogenous compounds by prokaryotes is called biological nitrogen fixation. Such microbes are called as diazotrophs or nitrogen fixers.
Eg : Free-living bacteria – Azotobacter, Clostridium.
Symbiotic bacteria – Rhizobium in the root nodules of Fabaceae members.
Blue green algae – Nostoc and Anabaena.

2) Nitrogen Assimilation :

1. The process of absorbing nitrates, Ammonia to produce organic nitrogen constituents is called nitrogen assimilation. It is the second step of nitrogen cycle.
2. Nitrates and Ammonia formed in the first step are absorbed by plants and converted and constitute the organic nitrogen.
   3) When plants are eaten by animals, this Organic nitrogen is passed on into the animal body.

3) Ammonification :

1. The process of conversion of organic nitrogenous compounds from the dead bodies of plants and animals into ammonia is called Ammonification. It is mineralization process.
2. The bacteria responsible for this are called Ammonifying bacteria.
   Eg: Bacillus ramosus, B. vulgaris, B. mycoides.

4) Nitrification :

1. This is fourth step of nitrogen cycle. It is an oxidative and an exergonic process.
2. The conversion of ammonia into nitrites and nitrates by bacteria is called nitrification. Sucfybacteria are called nitrifying bacteria. It occurs in two steps.

A) In the step, Ammonia is converted into nitrites by bacteria like Nitrosomonas and Nitrococcus.
2NH₃ + 3O₂ → 2NO₂^– + 2H⁺ + 2H₂O

B) In the next step, the nitrites are further oxidised to nitrates by Nitrobacter.
2NO₂^– + O₂ → 2NO₃^–

5) Denitrification :
This is final step in nitrogen cycle. It is also exergonic process released around 11,000 cal of energy. Conversion of nitrates of soil into molecular dinitrogen is called denitrification. Denitrification occurs in four steps
NO₃^– → NO₂^– → NO → N₂

This process is brought about by denitrifying bacteria like Thiobacillus denitrificans, Pseudomonas denitrificans and Micrococcus denitrificans.

Intext Questions

Question 1.
Who should be credited for initiation of Hydroponics?
Answer:
Julius von sachs (1860).

Question 2.
Are all the essential elements required by plants mineral elements? Explain.
Answer:
No. based upon the criteria of essentiality, only a few elements have been found to be essential for plant growth and metabolism. They are micro elements and microelements.

Question 3.
Which essential element is needed to activate the enzymes required for CO₂ fixatin?
Answer:
Mg⁺².

Question 4.
Name a cation and anion that maintain osmotic balance in cells?
Answer:
K⁺ and Cl^–

Question 5.
Which element is required for the formation of mitotic spidle?
Answer:
Calcium

Question 6.
What is the role of sulphur in plant life?
Answer:
Sulphur is present in two amino acids, cysteine and methionine. It is the main constituent of several coenzymes, vitamins (Thiamine, biotin, coenzyme A) and ferredoxin. It forms disulphide bridges which help in stabilizing protein structure.

Question 7.
Which micro element is required in more quantify than die other micronutrients?
Answer:
Iron.

Question 8.
Which element is necessary for the synthesis of the chief photosynthetic pigment without being its structural component?
Answer:
Iron, Magnesium

Question 9.
Which micronutrient necessary for photolysis of water is absorbed by plants in anionic form?
Answer:
Chlorine (Cl^–)

Question 10.
Which enzyme is activated by the 17^th essential element?
Answer:
Nickel acts as an activator for urease.

Question 11.
When is an element considered to be toxic?
Answer:
Any mineral ion concentration in tissues that reduces the dry weight of tissues by about 10 percent is considered toxic.

Question 12.
Which element when supplied in excess leads to appearence of brown spots surrounded by chlorotic venis?
Answer:
Magnesium.

Question 13.
Name an anaerobic, free living, photo-hetrotrophic nitrogen fixing bacterium.
Answer:
Rhodospirillum.

Question 14.
Which microorganism produces nitrogen-fixing nodules in Alnus?
Answer:
Frankia.

Question 15.
When the cross section of root nodules of ground nut plants are observed under microscope, they appear pinkish, why?
Answer:
This is due to the presence of leguminous haemoglobin or leg-haemoglobin which is a pink coloured pigment and is also called oxygen scavenger.

Question 16.
Apart from the cortical cells, which other cells are stimulated to divide by the bacteroids inside the root nodules?
Answer:
Inner cortex and pericycle cells.

Question 17.
What is the ratio of electrons and protons required for the fixation of atmospheric molecular nitrogen through biological mode?
Ans. 8H⁺ + 8e^– = 1 : 1.

Question 18.
What acts as oxygen scavenger in the legume-root nodule combination?
Answer:
Leg-hemoglobin.

Question 19.
In what why does aspargine differ from aspartic acid?
Answer:
Aspargine contains more nitrogen than aspartic acid.

Question 20.
Through which tissue the amino acids are transported inside the plant body?
Answer:
Xylem vessels.

Question 21.
Plants like the Picture and Venesfly trap have special nutritional adaptations. Name the essential element and its source for which they show such adaptations.
Answer:
Nitrogen.

Question 22.
Excess ‘Mn’ in soils leads to deficiency of Ca, Mg and Fe. Justify.
Answer:
Manganese competes with iron and Magnesium for uptake and with magnesium for binding with enzymes. Mn also inhibits calcium translocation in the shoot apex. Therefore excess of Mn may infact, induce deficiencies of Ca, Mg and Fe.

Question 23.
What acts as a reservoir of essential elements for plants? By what process is it formed?
Answer:
Soil, it is formed due to weathering and breakdown of Rocks.

Question 24.
Nitrogen fixation is shown by prokaryotes only. Why not by eukaryotes?
Answer:
In prokaryotes, nitrogenase enzyme which is a Mo-Fe protein is present and is capable of nitrogen reduction. It is absent in Eukaryotes.

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 1st Lesson Transport in Plants Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 1st Lesson Transport in Plants

Very Short Answer Questions

Question 1.
What are porins? What role do they play in diffusion?
Answer:
Porins are proteins that form huge pores in the outer membranes of the Plastids, mitochondria, and some bacteria, allowing molecules upto the size of small proteins to pass through.

Question 2.
Define water potential. What is the value of the water potential of pure water?
Answer:
Water potential is defined as the chemical potential of water and a measure of energy for reaction or movement. The value of the water potential of pure water is zero.

Question 3.
Differentiate osmosis from diffusion.
Answer:

Osmosis	Diffusion
The movement of water from low concentrated place to high concentrated place through a semipermeable membrane is called osmosis.	The movement of gases or molecules from high concentrated place to low concentrated place is called diffusion.

Question 4.
What are apoplast and symplast?
Answer:

Apoplast	Symplast
1) Apoplast is the path of water with in the plant that moves without crossing membranes.	1) Symplast is the path of water movement in the plant system that crosses the membranes.
2) It is faster process.	2) It is a slower process.

Question 5.
How does ffuttation differ from transniration?
Answer:

Guttation	Transpiration
1) The loss of water from the leaves of plants in the liquid form.	1) The loss of water in the form of water vapour from leaves.
2) It is an uncontrolled process.	2) It is a controlled process.

Question 6.
What are the physical properties of water responsible for the ascent of sap through xylem in plants?
Answer:
1) Cohesion :
Mutual attraction between water molecules.

2) Adhesion :
Attraction of water molecules to polar surface (such as the surface of trachery elements).

3) Transpiration pull:
Driving force for upward movement of water.

Question 7.
With reference to transportation of food within a plant cells, what are the sources and sink?
Answer:
Source is the part of the plant which synthesise the food. Sink is the part of the plant which utilizes depending on the season or the plants needs.

Question 8.
Does transpiration occurs at night? Give an example.
Answer:
Yes. In succulent plants, stomata opens during the night and remain closed during the day time. (Scotoactive stomata) Eg: Bryophyllum, Cacti.

Question 9.
Compare the pH of guard cells during the opening and closing of stomata.
Answer:
Increase in the pH of guard cells leads to the opening of stomata. Decrease in the pH of guard cells leads to closure of stomata.

Question 10.
In the wake of transpirational loss, why do the C₄ plants are of more efficient than C₃ plant?
Answer:
C₄ plants minimise water loss and fixes more CO₂ than C₃ plants.

Question 11.
What is meant by transport saturation how does it influence facilitated diffusion.
Answer:
Transport rate reaches a maximum when all of the protein transporters are being used is called transport saturation. It allows cell to select substances for uptake.

Question 12.
How does ABA bring about the closure of stomata under water stress conditions?
Answer:
Under water stress condition, ABA, a natural anti-transpirant drive the K⁺ ion put of the guard cells making them close.

Question 13.
Compare imbibing capacities of pea and wheat seeds.
Answer:
Proteinaceous pea seeds swell more on imbibition than starchy wheat seeds, because proteins have very high imbibing capacities compared to carbohydrates.

Short Answer Questions

Question 1.
Define and explain water potential
Answer:
“The measure of the relative tendency of water to move from one area to another is called water potential”. It is denoted by the Greek symbol Psi or Ψ and is expressed in pascals (Pa). It has two components namely solute potential and pressure potential.

a) Solute potential:
If some solute is added to pure water, the solution has fewer free water molecules and the concentration of water decreases reducing its water potential. The magnitude of this lowering due to dissolution of a solute is called solute potential. It is denoted as Ψ_s. It is always negative.

b) Pressure potential :
When water enters a plant ceil due to diffusion, causing a pressure to build up against the cell wall. This makes the cell turgid. The magnitude of increase in water potential in such turgid cell is called pressure potential It is usually positive and is denoted as Ψ_p.
Ψ = Ψ_S + Ψ_P

Question 2.
Write short note on facilitated diffusion.
Answer:
Facilitated diffusion :
The diffusion rate depends on the size of the substances. Obviously smaller substances diffuse faster. The diffusion of any substance across a membrane also depends on its solubility in lipids, which also move faster. Substances that have a hydrophilic moiety find it difficult to move through the membrane. Their movement has to be facilitated by membrane proteins without utilising metabolic energy and there must be concentration gradient.

This is called facilitated diffusion. It cannot cause net transport of molecules from low to high concentration, this would require input of energy. Facilitated diffusion is very specific, it allows cell to select substances for uptake. It is sensitive to inhibitors which react with protein side chains.

Some proteins allow diffusion only if two types of molecules move together. In asymport both molecules cross the membrane in the same direction, in an antiport, they move in opposite directions. When a molecule moves across a membrane independent of other molecules, the process is called uniport.

Question 3.
What is meant by plasmolysis? How is it practically useful to us?
Answer:
Plasmolysis is the process in plant cells where the cytoplasm pulls away from the cell wall due to the loss of water through osmosis. This occurs when cell is placed in a hypotonic solution, water moves out causes the shrinkage of protoplast leading to the seperation of plasma membrane from the cell wall in the comers called incipient plasmolysis. The salting of pickles and preserving of fish and meat in salt are good examples of practical applications.

Question 4.
How does ascent of sap occur in tall trees?
Answer:
Upward movement of water through xylem against gravitational force is called ascent of sap. The transpiration driven ascent of xylem sap depends on (a) Cohesion – mutual – attraction between water molecules (b) Adhesion – attraction of water molecules to polar surfaces (c) transpiration pull – driving force for upward movement of water. These properties give water high tensile strength and high capillarity.

In plants capillarity is aided by the small diameter of the tracheary elements. As water evaporates through the stomata, Since the thin film of water over the cells is continuous, it results in pulling of water, molecule by molecule into the leaf from the xylem. Also, because of lower concentration of water vapour in the atmosphere, water diffuses into the surrounding air. This creats transpiration pull. The forces generated by the transpiration can create pressure sufficient to lift a xylem sized column of water over 130 metres high.

Question 5.
Explain pressure flow hypothesis of translocation of sugars in plants.
Answer:
Glucose is prepared at the source is converted to sucrose, then moved into the companion cells and then into the living phloem sieve tube cells by active transport. Water in the adjacent xylem moves into the phloem by osmosis. As osmotic pressure builds up, the phloem sap moves to the cells which will use the sugar converting it into energy, starch or cellulose. As sugars are removed, the osmotic pressure decreases and water moves out of the phloem.

To explain this, Munch conducted one experiment. In this, he took two osmometers A and B. In ‘B’ he took concentrated sugar solution and in A, he took pure water. These two bulbs A and B are connected by a tube, ‘C’. He then, placed A and B bulbs in X and Y water tubs which are connected by tube ‘Z’. Due to osmosis, water moves from A to B, B to A through ‘C and then A-X and finally X-Y through Z occurs until the solution becomes isotonic. In this he compared ‘B’ bulb as source, A’ bulb as sink, ‘C’ tube as phloem, X apd Y tubs are xylem. .

Question 6.
Transpiration is necessary evil’. Explain.
Answer:
Transpiration has both beneficial and harmful effects. They are

Beneficial effects :

1. It helps in passive absorption of water.
2. It also helps in passive absorption of mineral salts by Mass flow mechanism.
3. It is the main force for ascent of sap.
4. It regulates the temperature of plant body and provides cooling effect.

Harmful effects :

1. Excessive transpiration makes the cells flaccid which retards growth.
2. Excessive transpiration leads to closure of stomata thus obstructing gaseous exchange.
   Hence transpiration is considered to be a necessary evil.

Question 7.
Transpiration and photosynthesis – a compromise. Explain.
Answer:
Transpiration has more than one purpose; it

1. Creates transpiration pull for absorption and transportation in plants
2. Supplies water for photosynthesis
3. Transports minerals from the soil to all parts of the plant
4. Cools leaf surface
5. Maintains the shape arid structure of the plants by keeping the cells turgid.

An actively photosynthesising plant has an insatiable need for water. Photosynthesis is limited by available water which can be swiftly depleted by transpiration. C₄ photo- synthetic system is one of the strategies for maximising the availability of CO₂ and minimizing water loss. C₄ plants are twice efficient than C₃ plants in fixing carbon and also water loss.

Question 8.
Explain the mechanism of opening and closing of stomata.
Answer:

Mechanism of opening and closing of stomata :
Levitt (1974) proposed K⁺ pump theory to explain the opening and closing of stomata. According to this, K⁺ ions are accumulated into guard cells from the subsidiary cells in the presence of light. This coupled efflux of protons leads to increase in pH of the guard cells. K⁺ ion accumulation is associated with influx of Cl^– ions to decrease the water potential of guard cells. Water enters into guard cells making them turgid. The outer walls of the guard cells are thin, expand out- wardly with the help of microfibrils in the cell walls of guard cells resulting in opening of stomata.

At night, the K⁺ and Cl^– ions move out of the guard cells due to which the water potential of guard cells increases and water stands moving out of guard cells leading to the closure of stomata.

Under water stress conditions ABA (Abscisic acid), a natural antitranspirant drives the K⁺ ions out of guard cell making them close.

Intext Questions

Question 1.
Differentiate uphill and down till transport.
Answer:

Uphill	Downhill
Proteins which transport substances from a low concentration to a high concentration is called uphill transport.	Proteins which transport substances from a High Concentration to a low concentration is called downhill transport.

Question 2.
Compare facilitated diffusion and simple diffusion.
Answer:

Facilitated diffusion	Simple diffusion
Movement of molecules along the concentration gradient, with the help of proteins.	Movement of molecules from one part of the cell to the other is called simple diffusion.

Question 3.
What happens when two solutions of different concentrations are separated by an egg membrane? State the reason.
Answer:
If two solutions are separated by an egg membrane, the solution moves from low concentrated solution to a high concentrated solution through egg membrane (semipermeable membrane) until the two solutions become equally concentrated. It is called osmosis.

Question 4.
In general in a plant which path of water movement is more and why?
Answer:
Transpiration pull. Generally due to transpiration, tension is created in mesophyll cells which withdraws water from stem → root → Root hair and finally from the soil. Thus water goes upwards in the form of a continuous column.

Question 5.
Why pinus seeds fail to germinate in the absence of mycorrhizae?
Answer:
Pinus plants have an obligate association with the mycorrhizae. The fungus only provides water and minerals. That is why seeds of pinus cannot germinate in the absence of mycorrhiza.

Question 6.
Why do stomata close under water stress conditions?
Answer:
In water stress conditions, ABA (Abscisie acid), a natural antitranspirants drives thfe K⁺ ions out of guard cells making the stomata close.

Question 7.
How are stomata distributed in a typical monocot plant?
Answer:
Stomata are equally distributed on both the surfaces in monocot also plant.

Question 8.
In what form the sugars are transported through phloem?
Answer:
Sucrose, other sugars, hormones and amino acids.

Question 9.
Why does the root endodermis transport ions in one direction only?
Answer:
The walls of the endodermis are suberised (casparian strips) and is impervious to water. So water is directed to wall regions that are not suberised into the cells proper through membranes. So because of suberin, it has the ability to transport water in one direction only.

Question 10.
If a ring of bark is removed from an actively growing plant, what will happen and why?
Answer:
In the absence of downward movement of food, the portion of the bark above the ring on the stem becomes swollen after a few weeks. This shows that, phloem is the tissue responsible for translocation of food.

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(e) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(e)

I. Find the I.F. of the following differential equations by transforming them into a linear form.

Question 1.
x[latex]\frac{dy}{dx}[/latex] – y = 2x² sec² 2x
Solution:
x[latex]\frac{dy}{dx}[/latex] – y = 2x² sec² 2x
[latex]\frac{dy}{dx}[/latex] – [latex]\frac{1}{x}[/latex] . y = 2x. sec² 2x
This is linear in x
I.F = e^{∫-[latex]\frac{1}{x}[/latex]dx} = e^{-log x} = e^{log 1/x} = [latex]\frac{1}{x}[/latex]

Question 2.
y[latex]\frac{dy}{dx}[/latex] – x = 2y³
Solution:
y[latex]\frac{dy}{dx}[/latex] – x = 2y³
[latex]\frac{dy}{dx}[/latex] – [latex]\frac{1}{y}[/latex].x = 2y²
I.F = e^{∫-[latex]\frac{1}{x}[/latex]dx} = e^{-log y} = e^{log 1/y} = [latex]\frac{1}{y}[/latex]

II. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}[/latex] + y tan x = cos³ x
Solution:

Solution is 2y = x cos x + sin x. cos² x + c. cos x

Question 2.
[latex]\frac{dy}{dx}[/latex] + y sec x = tan x
Solution:
I.F. = e^{∫sec x dx} = e^{log(secx + tan x)} = sec x + tan x
y. (sec x + tan x)
= ∫tan x (sec x + tan x)dx
= ∫(sec x. tan x + tan² x)dx
= ∫(sec x tan x + sec² x – 1)dx
Solution is
y(sec x + tan x) = sec x + tan x – x + c

Question 3.
[latex]\frac{dy}{dx}[/latex] – y tan x = e sec x. dx
Solution:
I.F. = e^{-∫tan x dx} = e^{log cos x} = cos x
y. cos x = ∫e^x.sec x. cos x dx = ∫ e^x dx
= e^x + c

Question 4.
x[latex]\frac{dy}{dx}[/latex] + 2y = log x.
Solution:
I.F. = e^{∫[latex]\frac{2}{x}[/latex]dx} = e^{2log x} = e^{log x²} = x²
Solution is

Question 5.
(1 + x²)[latex]\frac{dy}{dx}[/latex] + y = e^{tan-1 x}
Solution:

Question 6.
[latex]\frac{dy}{dx}+\frac{2y}{x}[/latex] = 2x².
Solution:
I.F. = e^{∫[latex]\frac{2}{x}[/latex]dx} = e^{2log x} = e^{log x²} = x²
y. x² = ∫2x⁴ dx = [latex]\frac{2x^5}{5}[/latex] + c

Question 7.
[latex]\frac{dy}{dx}+\frac{4x}{1+x^2}y=\frac{1}{(1+x^2)^2}[/latex]
Solution:

Question 8.
x[latex]\frac{dy}{dx}[/latex] + y = (1 + x)e^x
Solution:

Question 9.
[latex]\frac{dy}{dx}+\frac{3x^2}{1+x^3}y=\frac{1+x^2}{1+x^3}[/latex].
Solution:

Question 10.
[latex]\frac{dy}{dx}[/latex] – y = -2e^-x.
Solution:
I.F = e^∫-dx = e^-x
y. e^-x = -2∫e^-2x dx = e^-2x + c
y = e^-x + c. e^x

Question 11.
(1 + x²)[latex]\frac{dy}{dx}[/latex] + y = tan^-1 x.
Solution:

Put t = tan^-1 x so that dt = [latex]\frac{dx}{1+x^2}[/latex]
R.H.S = ∫t. e^tdt = t. e^t – ∫e^tdt
= t. e^t – e^t = e^t(t – 1)
Solution is y. e^{tan-1 x} = e^{tan-1 x} (tan^-11 x – 1) + c
y = tan^-1 x – 1 + c. e^{-tan-1 x}

Question 12.
[latex]\frac{dy}{dx}[/latex] + y tan x = sin x.
Solution:
I.F. =e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫ sin x. sec x dx = ∫tan x dx
= log sec x + c

III. Solve the following differential equations.

Question 1.
cos x. [latex]\frac{dy}{dx}[/latex] + y sin x = sec² x
Solution:
[latex]\frac{dy}{dx}[/latex] + tan x. y = sec³ x
I.F. = e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫sec⁴ x dx = ∫(1 + tan² x) sec² x
dx = tan x + [latex]\frac{\tan^3x}{3}[/latex] + c

Question 2.
sec x. dy = (y + sin x) dx.
Solution:
[latex]\frac{dy}{dx}=\frac{y+sin x}{sec x}[/latex] = y cos x + sin x. cos x
[latex]\frac{dy}{dx}[/latex] – y. cos x = sin x. cos x
I.F. = e^{-∫cos x dx} = e^{– sin x}
= y. e^{-sin x} = ∫ e^{-sin x}. sin x. cos x dx ……….. (1)
Consider ∫e^{-sin x}. sin x. cos x dx
t = – sin x ⇒ dt = -cos x dx
∫e^{-sin x}. sin x. cos x dx = + ∫e^t t dt
= t. e^t – e^t + c.
= e^{-sin x} (- sin x – 1) + c
y. e^{-sin x} = – e^{-sin x} (sin x + 1) + c
or y = – (sin x + 1) + c. e^{sin x}.

Question 3.
x log x.[latex]\frac{dy}{dx}[/latex] + y = 2 log x.
Solution:

Question 4.
(x + y + 1)[latex]\frac{dy}{dx}[/latex] = 1.
Solution:
[latex]\frac{dy}{dx}[/latex] = x + y + 1
[latex]\frac{dy}{dx}[/latex] – x = y + 1
I.F. = e^∫-dy e^-y
x . e^-y = ∫e^-y (y + 1) dy
= -(y + 1). e^-y + ∫e^-y. dy
= -(y + 1) e^-y – e^-y
= -(y + 2) e^-y+ c
x = -(y + 2) + c. e^-y

Question 5.
x(x – 1)[latex]\frac{dy}{dx}[/latex] – y = x³(x – 1)³
Solution:
[latex]\frac{dy}{dx}-\frac{1}{x(x-1)}[/latex]y = x²(x – 1)²

Question 6.
(x + 2y³)[latex]\frac{dy}{dx}[/latex] = y
Solution:

Solution is x = y(y² + c)

Question 7.
(1 – x²)[latex]\frac{dy}{dx}[/latex] + 2xy = x[latex]\sqrt{1-x^2}[/latex]
Solution:

Question 8.
x(x – 1)[latex]\frac{dy}{dx}[/latex] – (x – 2)y = x³(2x – 1)
Solution:


Solution is y(x – 1) = x²(x² – x + c)

Question 9.
[latex]\frac{dy}{dx}[/latex](x²y³ + xy) = 1
Solution:
[latex]\frac{dy}{dx}[/latex] = xy + x²y³
This is Bernoulli’s equation

Question 10.
[latex]\frac{dy}{dx}[/latex] + x sin 2y = x³ cos² y
Solution:

Question 11.
y² + (1 – [latex]\frac{1}{y}[/latex]).[latex]\frac{dy}{dx}[/latex] = 0
Solution:


Solution xy = 1 + y + cy.e^1/y

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d)

I. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}=-\frac{(12x+5y-9)}{5x+2y-4}[/latex]
Solution:
A non-homogenous equation
[latex]\frac{dy}{dx}=-\frac{(ax+by-9)}{a’x+b’y-c’}[/latex] where b = -a’
b = -5, a = 5 ⇒ b = -a
(5x + 2y-4)dy = -(12x + 5y-9) dx
(5x + 2y – 4)dy + (12x + 5y – 9) dx = 0
5 (x dy + y dx) + 2y dy – 4 dy + 12x dx – 9 dx = 0
integrating 5xy + y² – 4y + 6x² – 9x = c

Question 2.
[latex]\frac{dy}{dx}=-\frac{-3x-2y+5}{2x+3y+5}[/latex]
Solution:
b = – 2, a = 2 ⇒ b = -a
(2x + 3y + 5) dy = (- 3x – 2y + 5) dx
2x dy + 3y dy + 5 dy = -3x dx- 2y dx + 5 dx
2(x.dy + y dx) + By dy + 3x dx + 5 dy – 5 dx = 0
Integrating
2xy + [latex]\frac{3}{2}[/latex]y² + [latex]\frac{3}{2}[/latex]x² + 5y – 5x = c
4xy + 3y² + 3x² – 10x + 10y = 2c = c’
Solution is
4xy + 3(x² + y²)- 10(x – y) = c

Question 3.
[latex]\frac{dy}{dx}=\frac{-3x-2y+5}{2x+3y-5}[/latex]
Solution:
[latex]\frac{dy}{dx}=\frac{-(3x-2y+5)}{2x+3y-5}[/latex]
Here b = – 2, a¹ = 2
∵ b = -a¹
(2x + 3y – 5) dy = (-3x – 2y + 5) dx „
⇒ 2(x dy + y dx) + (3y – 5) dy + (3x – 5) dx – 0
⇒ 2d (xy) + (3y- 5) dy + (3x- 5) dx = 0
Now integrating term by term, we get
⇒ 2 ∫d (xy) + ∫(3y – 5)dy + ∫(3x – 5)dx = 0
⇒ 2xy + 3.[latex]\frac{y^2}{2}[/latex] – 5y + 3[latex]\frac{x^2}{2}[/latex] – 5x = [latex]\frac{c}{2}[/latex]
or) 3x² + 4xy + 3y² – 10x – 10y = c
Which is the required solution.

Question 4.
2(x – 3y + 1) [latex]\frac{dy}{dx}[/latex] = 4x – 2y + 1
Solution:
(2x – 6y + 2) dy = (4x – 2y + 1) dx
(2x – 6y + 2) dy – (4x – 2y + 1) dx = 0
2 (x dy + y dx) – 6y dy + 2 dy – 4x dx – dx = 0
Integrating
2xy – 3y² – 2x² + 2y – x = c

Question 5.
[latex]\frac{dy}{dx}=\frac{x-y+2}{x+y-1}[/latex]
Solution:
b = -1, a’ = 1 ⇒ b = -a’
(x + y – 1) dy = (x – y + 2) dx
(x + y – 1) dy = (x – y + 2) dx = 0
(x dy + y dx) + y dy – dy – x dx – 2 dx = 0
integrating
xy + [latex]\frac{y^2}{2}[/latex] – [latex]\frac{x^2}{2}[/latex] – y – 2x = c
2xy + y² – x² – 2y – 4x = 2c = c’

Question 6.
[latex]\frac{dy}{dx}=\frac{2x-y+1}{x+2y-3}[/latex]
Solution:
b = -1, a = 1 ⇒ b = -a’
(x + 2y – 3) dy = (2x – y + 1) dx
(x + 2y – 3) dy – (2x – y + 1) dx = 0
(x dy + y dx) 4- 2y dy – 3 dy – 2x dx – dx = 0
Integrating
xy + y² – x² – 3y – x = c

II. Solve the following differential equations.

Question 1.
(2x + 2y + 3) [latex]\frac{dy}{dx}[/latex] = x + y + 1
Solution:
[latex]\frac{dy}{dx}=\frac{x+y+1}{2x+2y+3}[/latex]

Multiplying with 9
6v + log (3v + 4) = 9x + 9c
6(x + y) + log [3(x + y) + 4] = 9x + c
i.e., log (3x + 3y + 4) = 3x – 6y + c

Question 2.
[latex]\frac{dy}{dx}=\frac{4x+6y+5}{3y+2x+4}[/latex]
Solution:

Multiplying with 64
8v + 9log (8v + 23) = 64x + 64c
8 (2x + 3y) – 64x + 9 log (16x + 24y + 23) = c’
Dividing with 8
2x + 3y – 8x + [latex]\frac{9}{8}[/latex] log (16x + 24y + 23) = c”
3y – 6x + [latex]\frac{9}{8}[/latex] log (16x + 24y + 23) = c”
Dividing with 3, solution is 3
y – 2x + [latex]\frac{3}{8}[/latex] log (16x + 24y + 23) = k

Question 3.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
Solution:

∫(2 + [latex]\frac{1}{v-1}[/latex])dv = 3∫dx
2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x + 2y – 3x + log (2x + y – 1) = c
Solution is x + 2y + log (2x + y – 1) = c

Question 4.
[latex]\frac{dy}{dx}=\frac{2y+x+1}{2x+4y+3}[/latex]
Solution:

Multiplying with 8
4v + log (4v + 5) = 8x + 8c
4(x + 2y) – 8x + log [4(x + 2y) + 5] = c’
Solution is
4x + 8y – 8x + log (4x + 8y + 5) = c’
8y – 4x + log (4x + 8y + 5) = c’

Question 5.
(x + y – 1) dy = (x + y + 1)dx
Solution:

v – log v = 2x + c
x + y – log (x + y) = 2x – c
(x – y) + log (x + y) = c is the required
solution.

III. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}=\frac{3y-7x+7}{3x-7y-3}[/latex]
Solution:
Let x = x + h, y = y + k so that [latex]\frac{dy}{dx}=\frac{dy}{dx}[/latex]


3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1)
14ln x – ln c = – 10ln (v + 1) – 4 ln (v – 1)
ln (v + 1)⁵ + ln (v – 1)² + ln x⁷ = ln c
(v +1)⁵. (v – 1)². x⁷ = c
([latex]\frac{y}{x}[/latex] + 1)⁵ ([latex]\frac{y}{x}[/latex] – 1)².x⁷ = c
(y – x)² (y + x)⁵ = c
[y – (x – 1 )]² (y + x – 1 )⁵ = c
Solution is [y-x + 1 ]² (y + x – 1)⁵ = c.

Question 2.
[latex]\frac{dy}{dx}=\frac{6x+5y-7}{2x+18y-14}[/latex]
Solution:



Multiplying with (3V – 2)(2V + 1)
2 + 18V = A(2V + 1) + B(3V – 2)

2 log (3V- 2)+ log (2V+ 1) = – 3 log X + log c
log (3V – 2)².(2V + 1) + log X³ = log c
log X³(3V – 2)² (2V + 1) = log c
x³(3V – 2)² (2V + 1) = c

Solution is (3y – 2x – 1)² (x + 2y – 2) = 343c = c”.

Question 3.
[latex]\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}[/latex] = 0
Solution:
[latex]\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}[/latex] = 0
x = X + h, y = Y + k


5V + 7 = A(V + 2) + B (V + 1)
V = -1 ⇒ 2 = A(-1 + 2) = A ⇒ A = 2
V = -2 ⇒ -3 = B(-2 + 1) = -B, B = 3
∫([latex]\frac{2}{(V+1)}+\frac{3}{(V+2)}[/latex])dv = ∫[latex]\frac{dx}{X}[/latex]
2 log (V + 1) + 3 log (V + 2) = – 5 log X + c
c = 2 log (V + 1) + 3 log (V + 2) + 5 log X
= log (V + 1)². (V + 2)³. X⁵
= log([latex]\frac{2}{(V+1)})[/latex])².([latex]\frac{3}{(V+2)}[/latex])³. X⁵
= log[latex]\frac{(Y+X)^2}{X^2}[/latex] [latex]\frac{(Y+2X)^3}{X^3}[/latex] . X⁵
⇒ (Y + X)² . (Y + 2X)³ = e^c = c’
(Y + 1 – X – 2)² (Y + 1 – 2x – 4)³ = c
Solution is (x + y – 1)² (2x + y – 3)³ = c.

Question 4.
(x – y – 2) dx + (x – 2y – 3) dy = 0
Solution:
Given equation is [latex]\frac{dy}{dx}=\frac{-x+y+2}{x-2y-3}[/latex]
Let x = X + h, y = Y + k




is the required solution.

Question 5.
(x – y) dy = (x + y + 1) dx
Solution:

Question 6.
(2x + 3y – 8) dx = (x + y – 3) dy
Solution:

Question 7.
[latex]\frac{dy}{dx}=\frac{x+2y+3}{2x+3y+4}[/latex]
Solution:
Let x = X + h, y = Y + k so that [latex]\frac{dY}{dX}=\frac{dy}{dx}[/latex]

Choose h and k so that
h + 2k + 3 = 0
2h + 3k + 4 = 0

This is a homogeneous equation

Question 8.
[latex]\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}[/latex]
Solution:
Given equation is [latex]\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}[/latex]
Let x = X + h, y = Y + k so that [latex]\frac{dY}{dX}=\frac{dy}{dx}[/latex]

∴ [latex]\frac{dY}{dX}=\frac{2X+9Y}{6X+2Y}[/latex]
This is a homogeneous equation

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(c)

I.

Question 1.
Express x dy – ydx = [latex]\sqrt{x^2+y^2}[/latex] dx in the form F ([latex]\frac{y}{x}[/latex]) = ([latex]\frac{dy}{dx}[/latex]).
Solution:
x. dy – y dx = [latex]\sqrt{x^2+y^2}[/latex] dx
[latex]\frac{dy}{dx}[/latex] – y = [latex]\sqrt{x^2+y^2}[/latex]

Question 2.
Express (x – y Tan^-1 [latex]\frac{y}{x}[/latex])dx + x Tan^-1[latex]\frac{y}{x}[/latex] dy = 0 in the form F([latex]\frac{y}{x}[/latex]) = [latex]\frac{dy}{dx}[/latex].
Solution:

Question 3.
Express x[latex]\frac{dy}{dx}[/latex] = y(log y – log x + 1) in the from F ([latex]\frac{y}{x}[/latex]) = [latex]\frac{dy}{dx}[/latex]
Solution:
x . [latex]\frac{dy}{dx}[/latex] = y(log y – log x + 1)
[latex]\frac{dy}{dx}[/latex] = [latex]\frac{y}{x}[/latex](log[latex]\frac{y}{x}[/latex] + 1)

II. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}=\frac{x-y}{x+y}[/latex]
Solution:
[latex]\frac{dy}{dx}=\frac{x-y}{x+y}[/latex]
Put y = vx
[latex]\frac{dy}{dx}[/latex] = v + x[latex]\frac{dv}{dx}[/latex]

Question 2.
(x² + y²) dy = 2xy dx
Solution:
(x² + y²) dy = 2xy dx

1 + v² = A(1 – v²) + Bv(1 – v) + Cv(1 + v)
v = 0 ⇒ = A
v = 1 ⇒ 1 + 1 = C(2) ⇒ c = 1
v = -1 ⇒ 1 + 1 = B(-1) (2) ⇒ 2 = -2B
B = -1

Question 3.
[latex]\frac{dy}{dx}=\frac{-(x^2+3y^2)}{3x^2+y^2}[/latex]
Solution:
[latex]\frac{dy}{dx}=\frac{-(x^2+3y^2)}{3x^2+y^2}[/latex]
Put y = vx

Multiplying with (v + 1)³
3 + v² = A(v + 1)² + B(v + 1) + C
v = – 1 ⇒ 3 + 1 = C ⇒ C = 4
Equating the co-efficients of v²
A = 1
Equating the co-efficients of v
0 = 2A + B
B = -2A = -2

Question 4.
y²dx + (x² – xy)dy = 0
Solution:

v – log v = log x + log k
v = log v + log x + log k
= log k (vx)
[latex]\frac{y}{x}[/latex] = log ky
Solution is ky = e^y/x

Question 5.
[latex]\frac{dy}{dx}=\frac{(x+y)^2}{2x^2}[/latex]
Solution:

Question 6.
(x² – y²)dx – xy dy = 0
Solution:
(x² – y²)dx – xy dy = 0
(x² – y²)dx = xy . dy

Question 7.
(x²y – 2xy²)dx = (x³ – 3x²y)dy
Solution:
(x²y – 2xy²)dx = (x³ – 3x²y)dy

Question 8.
y²dx + (x² – xy + y²) dy = 0
Solution:
y²dx = – (x² – xy + y²)dy

1 – v + v² = A(1 + v²) + (Bv + C)v
v  =  0 ⇒ 1 = A
Equating the co-efficients of v²
1 = A + .B ⇒ B = 0
Equating the co-efficients of v
-1 = C

Question 9.
(y² – 2xy)dx + (2xy – x²)dy = 0
Solution:
(y² – 2xy)dx + (2xy – x²)dy = 0
(2xy – x²)dy = – (y² – 2xy)dx

2v – 1 = A(1 – v) + Bv
v = 0 ⇒ -1 = A ⇒ A = -1
v = 1 ⇒ 1 = B ⇒ B = 1

Question 10.
[latex]\frac{dy}{dx}+\frac{y}{x}=\frac{y^2}{x^2}[/latex]
Solution:
[latex]\frac{dy}{dx}+\frac{y}{x}=\frac{y^2}{x^2}[/latex]

Question 11.
x dy – y dx = [latex]\sqrt{x^2+y^2}[/latex]
Solution:
x dy – y dx = [latex]\sqrt{x^2+y^2}[/latex]

Question 12.
(2x – y)dy = (2y – x)dx
Solution:


⇒ (y – x)² = c²(y + x)²(y² – x²)
⇒ y – x = c²(y + x)³
⇒ (x + y)³ = c(x – y) where c = [latex]\frac{-1}{c^2}[/latex]
∴ (x + y)³ = c(x – y)

Question 13.
(x² – y²)[latex]\frac{dy}{dx}[/latex] = xy
Solution:

Question 14.
2[latex]\frac{dy}{dx}=\frac{y}{x}+\frac{y^2}{x^2}[/latex]
Solution:
Put y = vx

(y – x)² = y²c²x
Solution is y²x = c(x – y)²

III.

Question 1.
Solve : (1 + e^x/y)dx + e^x/y(1 – [latex]\frac{x}{y}[/latex])dy = 0.
Solution:
Put x = vy

Question 2.
Solve : x sin [latex]\frac{y}{x}.\frac{dy}{dx}[/latex] = y sin [latex]\frac{y}{x}[/latex] – x
Solution:
Dividing with x, we have

Question 3.
Solve : x dy = (y + x cos² [latex]\frac{y}{x}[/latex])dx
Solution:
x.[latex]\frac{dy}{dx}[/latex] = y + xcos² [latex]\frac{y}{x}[/latex]

Question 4.
Solve : (x – y log y + y log x)dx + x(log y – log x)dy = 0
Solution:
Dividing with x. dx we get

Question 5.
Solve : (y dx + x dy) x cos [latex]\frac{y}{x}[/latex] = (x dy – y dx) y sin [latex]\frac{y}{x}[/latex].
Solution:
The given equation can be written as

∴ This is a homogeneous equation

Question 6.
Find the equation of a curve whose gradient is [latex]\frac{dy}{dx}=\frac{y}{x}-\cos^2\frac{y}{x}[/latex], where x > 0, y > 0 and which passes through the point (1, [latex]\frac{\pi}{4}[/latex]).
Solution:

tan v = – log |x| + c
This curve passes through (1, [latex]\frac{\pi}{4}[/latex])
tan [latex]\frac{\pi}{4}[/latex] = c – log 1
c = 1
∴ Equation of the curve is
tan v = 1 – log |x|
tan [latex]\frac{y}{x}[/latex] = 1 – log |x|

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b)

I.

Question 1.
Find the general solution of [latex]\sqrt{1-x^2}[/latex] dy + [latex]\sqrt{1-y^2}[/latex] dx = 0.
Solution:
Given differential equation is

sin^-1 y = – sin^-1 x + c
Solution is sin^-1 x + sin^-1 y = c, where c is a constant.

Question 2.
Find the general solution of [latex]\frac{dy}{dx}=\frac{2y}{x}[/latex].
Solution:
[latex]\frac{dy}{dx}=\frac{2y}{x}[/latex]
∫[latex]\frac{dy}{dx}[/latex] = 2∫[latex]\frac{2y}{x}[/latex]
log c + log y = 2 log x
log cy = log x²
Solution is cy = x², where c. is a constant.

II. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}=\frac{1+y^2}{1+x^2}[/latex]
Solution:
[latex]\frac{dy}{dx}=\frac{1+y^2}{1+x^2}[/latex]
∫[latex]\frac{dy}{1+y^2}[/latex] = ∫[latex]\frac{dx}{1+x^2}[/latex]
tan^-1 y = tan^-1 x + tan^-1c where c is a constant.

Question 2.
[latex]\frac{dy}{dx}[/latex] = e^y-k
Solution:
[latex]\frac{dy}{dx}=\frac{e^y}{e^x}[/latex]
[latex]\frac{dy}{e^y}=\frac{dx}{e^x}[/latex]
∫e^-xdx = ∫e^-ydy
-e^-x = -e^-y + C
e^-y = e^-x + c where c is a constant.

Question 3.
(e^x + 1) y dy + (y + 1) dx = 0
Solution:
(e^x + 1 )y. dy = – (y + 1) dx

y – log (y + 1) = log (e^-x + 1) + log c
⇒ y – log (y + 1) = log c (e^-x + 1)
⇒ y = log (y + 1) + log c (e^-x + 1)
y = log c (y + 1) (e^-x +1)
Solution is
e^y = c(y + 1) (e^-x +1)

Question 4.
[latex]\frac{dy}{dx}[/latex] = e^x-y + x²e^-y
Solution:
[latex]\frac{dy}{dx}[/latex] = e^x-y + x² . e^-y
= [latex]\frac{e^x}{e^y}=\frac{x^2}{e^y}[/latex]
∫e^y . dy = ∫(e^x + x²) dx
Solution is
e^y = e^x + [latex]\frac{x^3}{3}[/latex] + c

Question 5.
tan y dx + tan x dy = 0
Solution:
tan y dx = – tan x dy

log sin x = – log sin y + log c
log sin x + log sin y = log c
log (sin x . sin y) = log c
⇒ sin x . sin y = c is the solution

Question 6.
[latex]\sqrt{1+x^2}[/latex]dx + [latex]\sqrt{1+y^2}[/latex]dy = 0
Solution:
[latex]\sqrt{1+x^2}[/latex]dx = -[latex]\sqrt{1+y^2}[/latex]dy
Integrating both sides we get
∫[latex]\sqrt{1+x^2}[/latex]dx = -∫[latex]\sqrt{1+y^2}[/latex]dy
Integrating both sides we get

Question 7.
y – x[latex]\frac{dy}{dx}[/latex] = 5(y² + [latex]\frac{dy}{dx}[/latex])
Solution:
y – 5y² = (x + 5)[latex]\frac{dy}{dx}[/latex]
[latex]\frac{dx}{x+5}=\frac{dy}{y(1-5y}[/latex]
Integrating both sides

Question 8.
[latex]\frac{dy}{dx}=\frac{xy+y}{xy+x}[/latex]
Solution:

III. Solve the following differential equations.

Question 1.
[latex]\frac{dy}{dx}=\frac{1+y^2}{(1+x^2)xy}[/latex]
Solution:

log (1 + y²) = log x² – log (1 + x²) + log c
log (1 + x²) + log (1 + y²) = log x² + log c
Solution is (1 + x²) (1 + y²) = cx²

Question 2.
[latex]\frac{dy}{dx}[/latex] + x² = x² e^3y
Solution:

log(1 – e^-3y) = x³ + c'(c’ = 3c)
Solution is
1 – e^-3y = e^x³ . k(k = e^c’)

Question 3.
(xy² + x)dx+(yx²+y)dy = 0.
Solution:
(xy² + x) dx + (yx² + y) dy = 0
x(y² + 1) dx + y (x² + 1) dy = 0
Dividing with (1 + x²) (1 + y²)
[latex]\frac{x dx}{1+x^2}+\frac{y dy}{1+y^2}[/latex] = 0
Integrating
∫[latex]\frac{x dx}{1+x^2}[/latex] + ∫[latex]\frac{y dy}{1+y^2}[/latex] = 0
[latex]\frac{1}{2}[/latex] [(log (1 + x²) + log (1 + y²)] = log c
log (1 + x²) (1 + y²) = 2 log c = log c²
Solution is (1 + x²) (1 + y²) = k when k = c².

Question 4.
[latex]\frac{dy}{dx}[/latex] = 2y tanh x
Solution:
[latex]\frac{dy}{dx}[/latex] = 2y tanh x
[latex]\frac{dy}{y}[/latex] = 2 tanh x dx
Integrating both sides we get
∫[latex]\frac{dy}{y}[/latex] = 2 ∫ tanh x dx
log y = 2 log |cosh x| + log c
lny = 2ln cosh x + In c
y = c cos²h x

Question 5.
sin^-1 [latex]\frac{dy}{dx}[/latex] = x + y
Solution:
[latex]\frac{dy}{dx}[/latex] = sin(x + y)
x + y = t
1 + [latex]\frac{dy}{dx}=\frac{dt}{dx}[/latex]
[latex]\frac{dt}{dx}[/latex] – 1 = sin t
[latex]\frac{dt}{dx}[/latex] = 1 + sin t
Integrating both sides we get
∫[latex]\frac{dt}{1+\sin t}[/latex] = ∫dx
∫[latex]\frac{1-\sin t}{\cos^2 t}[/latex] dt = x + c
∫sec² t dt – ∫tan t . sec t dt = x + c
tan t – sec t = x + c
⇒ tan (x + y) – sec (x + y) = x + c

Question 6.
[latex]\frac{dy}{dx}+\frac{y^2+y+1}{x^2+x+1}[/latex] = 0
Solution:
[latex]\frac{-dy}{y^2+y+1}=\frac{dx}{x^2+x+1}[/latex]
Integrating both sides dy

Question 7.
[latex]\frac{dy}{dx}[/latex] = tan² (x + y)
Solution:
[latex]\frac{dy}{dx}[/latex] = tan² (x + y)
put v = x + y

2v + sin 2v = 4x + c’
2(x + y) + sin 2(x + y) = 4x + c’
x – y – [latex]\frac{1}{2}[/latex]sin [2(x + y)] = c

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a)

I.

Question 1.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = ce^x – be^-x + x².
Solution:
Given equation is xy = ce^x – be^-x + x²
Differentiating w.r.to x, we get
xy₁ + y = ce^x – be^-x + 2x.
Again differentiating w.r.to x, we get
xy₂ + y₁ + y₁ = ce^x – be^-x + 2
xy₂ + 2y₂ = xy – x² + 2
Arbitary constants a and b are eliminated.
∴ The order is 2.

Question 2.
Find the order of the differential equation of the family of all circles with their centres at the origin.
Solution:
Equation of the circle with centre at origin is x² + y² = r²
Order = no .of arbitrary constants = 1

II.

Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets.
i) y = c(x – c)² ; (c)
Solution:
y = c(x – c)² ………….. (1)
Differentiating w.r. to x
y₁ = c. 2(x – c) ………….. (1)
Dividing (2) by (1)
[latex]\frac{y_2}{y}=\frac{2c(x-c)}{c(x-c)^2}[/latex]
x – c = [latex]\frac{2y}{y_1}[/latex]
c = x – [latex]\frac{2y}{y_1}[/latex]
Substituting in (1)
y = x – [latex]\frac{2y}{y_1}[/latex](x – [latex]\frac{2y}{y_1}[/latex])²
= [latex]\frac{xy_1-2y}{y_1}.\frac{4y^2}{y_1^2}[/latex]
y.y³₁ = 4y²(xy₁ – 2y)
i.e., y³₁ = 4y (xy₁ – 2y)
= 4xyy₁ – 8y²
([latex]\frac{dy}{dx}[/latex])³ – 4xy[latex]\frac{dy}{dx}[/latex] + 8y² = 0

ii) xy = ae^x + be^-x; (a, b)
Solution:
xy = ae^x + b.e^-x
Differentiating w.r.t. x
x . y₁ + y = ae^x – b . e^-x
Differentiating again w.r.t. x
xy₂ + y₁ + y₁ = ae^x + be^-x = xy
[latex]\frac{d^2y}{dx^2}[/latex] + 2[latex]\frac{dy}{dx}[/latex] – xy = 0

iii) y = (a + bx)e^kx ; (a, b)
Solution:
y = (a + bx)e^kx
Differentiating w.r.t. x
y₁ = (a + bx) e^kx. k + e^kx . b
= k . y + b.e^kx
y₁ – ky = b.e^kx …………. (1)
Differentiating again w.r.t. x
y₂ – ky₁ = kb e^kx
= k(y₁ – ky) ………… (2)
= ky₁ – k²y
[latex]\frac{d^2y}{dx^2}[/latex] – 2k[latex]\frac{dy}{dx}[/latex] + k²y = 0

iv) y = a cos (nx + b); (a, b)
Solution:
y = a cos (nx + b)
y₁ = – a sin (nx + b) n
y₂ = – an. cos (nx + b) n
= – n² . y
[latex]\frac{d^2y}{dx^2}[/latex]+n².y = 0

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The rectangular hyperbolas which have the co-ordinate axes as asymptotes.
Solution:
Equation of the rectangular hyperbolas is xy = c² where c is arbitrary constant
Differentiating w.r.t. x
x[latex]\frac{dy}{dx}[/latex] + y = 0

ii) The ellipses with centres at the origin and having co-ordinate axes as axes.
Solution:
Equation of ellipse is
[latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}[/latex] = 1
Differentiating w.r.to ‘x’ we get

Multiply (ii) by x and subtract from (i)

III.

Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets :
i) y = ae^3x + be^3x; (a, b)
Solution:
Differentiating w.r. to x
y₁ = 3ae^3x + 4be^4x
y₁ – 3a. e^3x = 4b.e^4x
= 4(y – a. e^3x)
= 4y – 4a. e^3x
y₁ – 4y = – a.e^3x ………… (1)
Differentiating again w.r.t. x
y₂ – 4y₁ = – 3a. e^3x
= 3 (y₁ – 4y) by (1)
= 3y₁ – 12y
[latex]\frac{d^2y}{dx^2}[/latex] – 7[latex]\frac{dy}{dx}[/latex] + 12y = 0

ii) y = ax² + bx; (a, b)
Solution:

Adding all three equations we get
x²[latex]\frac{d^2y}{dx^2}[/latex] – 2x[latex]\frac{dy}{dx}[/latex] + 2y = 0

iii) ax² + by² = 1; (a, b)
Solution:
ax² + by² = 1
by² = 1 – ax² ………….. (1)
Differentiating w.r.t. x
2by. y₁ = – 2ax ………….. (2)
Dividing (2) by (1)
[latex]\frac{by.y_1}{by^2}=\frac{-ax}{1-ax^2}[/latex]

Differentiating w.r.t. x

iv) xy = ax² + [latex]\frac{b}{x}[/latex]; (a, b)
Solution:
xy = ax² + [latex]\frac{b}{x}[/latex]
x²y = ax³ + b
Differentiating w.r.t. x
x²y₁ + 2xy = 3ax²
Dividing with x
xy₁ + 2y = 3ax ………… (1)
Differentiating w.r.t. x
xy₂ + y₁ + 2y₁ = 3a
xy₂ + 3y₁ = 3a ………… (2)
Dividing (1) by (2)
[latex]\frac{xy_1+2y}{xy_2+3y_1}=\frac{3ax}{3a}=x[/latex]
Cross multiplying
xy₁ + 2y = x²y₂ + 3xy
x²y₂ + 2xy₁ – 2y = 0
x²[latex]\frac{d^2y}{dx^2}[/latex] + 2x[latex]\frac{dy}{dx}[/latex] – 2y = 0

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The circles which touch the Y – axis at the origin.
Solution:
Equation of the required circle is
x² + y² + 2gx = 0
x² + y² = – 2gx …………. (1)
Differentiating w.r. t x
2x + 2yy₁ = – 2g ……….. (2)
Substituting in (1)
x² + y² = x(2x + 2yy₁) by (2)
= 2x² + 2xyy₁
yy² – 2xyy₁ – 2x² = 0
y² – x² = 2xy[latex]\frac{dy}{dx}[/latex]

ii) The parabolas each of which has a latus rectum 4a and whose axes are parallel to X – axis.
Solution:

Equation of the required parabola is
(y – k)² = 4a (x – h) …………. (1)
Differentiating w.r.t. x
2(y – k)y₁ = 4a …………. (2)
Differentiating w.r.t. x
(y – k) y₂ + y²₁ = 0 …………. (3)
From (2), y – k = [latex]\frac{2a}{y_1}[/latex]
Substituting in (3)
[latex]\frac{2a}{y_1}[/latex].y₂ = y²₁ = 0
2ay₂ + y³₁ = 0

iii) The parabolas having their foci at the origin and axis along the X – axis.
Solution:
Equation of parabola be y² = 4a(x + a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(d)

I.

Question 1.
Find the area of the region enclosed by the given curves.
i) y = cos x, y = 1 – [latex]\frac{2x}{\pi}[/latex]
Solution:
Equations of the given curves are
y = cos x ………….. (1)
y = 1 – [latex]\frac{2x}{\pi}[/latex] ………….. (2)
Eliminating y from eq’s (1) and (2)
cos x = 1 – [latex]\frac{2x}{\pi}[/latex]
When x = [latex]\frac{\pi}{2}[/latex], cos x = cos[latex]\frac{\pi}{2}[/latex] = 0
1 – [latex]\frac{2}{\pi}[/latex], x = [latex]\frac{2}{\pi}[/latex] . [latex]\frac{\pi}{2}[/latex] = 1 – 1 = 0
When x = 0, cos x = cos 0 = 1
1 – [latex]\frac{2x}{\pi}[/latex] = 1 – 0 = 1
∴ Point of intersection are A = ([latex]\frac{\pi}{2}[/latex], 0) B = [π – 1]

Question 2.
y =cos x, y = sin 2x, x = 0, x = [latex]\frac{\pi}{2}[/latex].
Solution:

Question 3.
y = x³ + 3, y = 0, x = -1, x = 2.
Solution:
Required area PABQ

Question 4.
y = e^x, y = x, x = 0, x = 1.
Solution:

Question 5.
y = sin x, y = cos x; x = 0, x = [latex]\frac{\pi}{2}[/latex].
Solution:

Between 0 and [latex]\frac{\pi}{4}[/latex].
cos x > sin x
Between [latex]\frac{\pi}{4}[/latex] and [latex]\frac{\pi}{2}[/latex]
cos x < sin x
Required area

Question 6.
x = 4 – y², x = 0.
Solution:
The given parabola x = 4 – y² meets, the x – axis at A(4, 0) and Y – axis at P(0, 2) and Q(0, -2).

The parabola is symmetrical about X – axis

Required area = 2 Area of OAP

Question 7.
Find the area enclosed with in the curve |x| + |y| = 1
Solution:

II.

Question 1.
x = 2 – 5y – 3y², x = 0.
Solution:
Solving the equation of given curves
2 – 5y – 3y² = 0
3y² + 5y – 2 = 0
(y + 2)(3y – 1) = 0 y = -2 or [latex]\frac{1}{3}[/latex]

Question 2.
x² = 4y, x = 2, y = 0.
Solution:

Question 3.
y² = 3x, x = 3.
Solution:

The parabola is symmetrical about X – axis
Required area = 2[latex]\int_0^3[/latex]√3. √x dx

Question 4.
y = x², y = 2x.
Solution:
Given equation are y = x² ………….. (1)
y = 2x …………. (2)

Eliminating y, we get x² = 2x
x² – 2x = 0
x(x – 2) = 0
x = 0 or x = 2
y = 0, or y = 4

Point of intersection are O(0, 0), A(2, 4)

Question 5.
y = sin 2x, y = √3 sin x, x = 0, x = [latex]\frac{\pi}{6}[/latex].
Solution:
Given equation are y = sin 2x ………… (1)
y = √3 sin x …………. (2)
sin 2x = √3 sin x
2 sin x. cos x = √3 sin x
sin x = 0 or 2 cos x = [latex]\frac{\sqrt{3}}{2}[/latex]
x = 0, cos x = [latex]\frac{\sqrt{3}}{2}[/latex] ⇒ x = [latex]\frac{\pi}{6}[/latex]

Question 6.
y = x², y = x³.
Solution:
Given equations are y = x² ………….. (1)
y = x³ ………. (2)

From equation (1) and (2) x² = x³
x³ – x² = 0
x²(x – 1) = 0
x = 0 or 1

Question 7.
y = 4x – x², y = 5 – 2x
Solution:

y = 4x – x² ………… (i)
y = 5 – 2x …………..(ii)
y = -([x – 2]²) = 4
y – 4 = -(x – 2)²
Solving equations (i) and (ii) we get
4x – x² = 5 – 2x
x² – 6x + 5 = 0
(x – 5)(x – 1 ) = 0
x = 1, 5

Question 8.
Find the area in Sq. units bounded by the x – axis, part of the curve y = 1 + [latex]\frac{8}{x^2}[/latex] and the ordinates x = 2 and x = 4.
Solution:
Given equations y = 1 + [latex]\frac{8}{x^2}[/latex]

Question 9.
Find the area of the region bounded by the parabolas y² = 4x and x² = 4y.
Solution:
Equations of the given curve are
y² = 4x
x² = 4y
([latex]\frac{x^2}{4}[/latex])² = 4x
[latex]\frac{x^4}{16}[/latex] = 4x
x⁴ = 64x ⇒ x⁴ = 0 or x³ = 64, x = 4

Question 10.
Find the area bounded by the curve y = lnx the X – axis and the straight line x = e.
Solution:
Equation of the curve is y = lnx
x = 1 ⇒ y = 0
The curve y = lnx meets
X – axis at C(1, 0)

Required area = [latex]\int_1^e[/latex]lnx dx
= (x.lnx)^e₁ – [latex]\int_1^e[/latex]x.[latex]\frac{1}{x}[/latex] dx
= (e.ln e – 1.ln 1) – (x)^e₁
= e – (e – 1)
= e – e + 1 = 1 Sq.unit.

III.

Question 1.
y = x² + 1, y = 2x – 2, x = -1, x = 2.
Solution:
Equation of the curve are
y = x² + 1 …………. (1)
y = 2x – 2 ………….. (2)

Area between the given curves

Question 2.
y² = 4x, y² = 4(4 – x).
Solution:
Equations of the curve are y² = 4x ………… (1)
y² = 4(4 – x) …………. (2)
Eliminating y, we get
4x = 4(4 – x)
2x = 4 ⇒ x = 2
Substituting in equation (1), y² = 8
y = ± 2√2

Points of intersection are
A(2, 2√2), B(2, -2√2)
Required area is symmetrical about X – axis
Area OACB

Question 3.
y = 2 – x², y = x².
Solution:

y = 2 – x² …………. (1)
y = x² …………. (2)
x² = -(y – 2)
From equation (2)
2 – x² = x²
2 = 2x² or x² = 1
x = ±1
Area bounded by two curve be

Question 4.
Show that the area enclosed between the curve y² = 12(x + 3) and y² = 20(5 – x) is 64[latex]\sqrt{\frac{5}{3}}[/latex].
Solution:
Equation of the curve are
y² = 12(x + 3) ……….. (1)
y² = 20(5 – x) ……….. (2)
Eliminating y
12(x + 3) = 20(5 – x)
3x + 9 = 25 – 5x
8x = 16
x = 2
y² = 12(2 + 3) = 60
y = √60 = ±2√15

Points of intersection are B’ (2, 2√15)
B’ (+2, -2√15)
The required area is symmetrical about X – axis
Area ABCB’

Question 5.
Find the area of the region {(x, y)/x² – x – 1 ≤ y ≤ -1}
Solution:

Question 6.
The circle x² + y² = 8 is divided into two parts by the parabola 2y = x². Find the area of both the parts.
Solution:
Equations of the curves are
x² + y² = 8 ………… (1)
2y = x² ………… (2)
Eliminating y between equations (1) and (2)

Let x² = t
4t + t² = 32
t² + 4t – 32 = 0
(t + 8)(t – 4) = 0
t = -8 (not possible) x² = 4 ⇒ x = ±2

As curve is symmetric about Y – axis, total area be

Question 7.
Show that the area of the region bounded [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}[/latex] = 1 (ellipse) is π ab. also deduce the area of the cricle x² + y² = a².
Solution:

The ellipse is symmetrical about X and Y axis
Area of the ellipse = 4 Area of CAB
= 4.[latex]\frac{\pi}{4}[/latex] ab
Equation of elliple = [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}[/latex] = 1

Substituting b = a, we get the circle
x² + y² = a²
Area of the circle = πa(a) = πa² sq. units.

Question 8.
Find the area of region enclosed by the curves y = sin πx, y = x² – x, x = 2.
Solution:
Required area

Question 9.
Let AOB be the positive quadrant of the ellipse [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}[/latex] = 1 with OA = a, OB = b. Then show that the area bounded the chord AB and the arc AB of the elliple is [latex]\frac{(\pi-2) a b}{4}[/latex].
Solution:
Let OA = a, OB = b
Equation of AB is [latex]\frac{x}{a}+\frac{y}{b}[/latex] = 1
[latex]\frac{y}{b}[/latex] = 1 – [latex]\frac{x}{a}[/latex]
y = b(1 – [latex]\frac{x}{a}[/latex])

Question 10.
Prove that curves y² = 4x and x² = 4y divide the area of the square bounded by the lines x = 0, x = 4, y = 4 and x = 0 into three equal parts.
Solution:

The given equations are y² = 4x …………. (1)
x² = 4y …………. (2)
The points of intersection are O(0, 0) A(4, 4)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(c)

I. Evaluate the following definite integrals.

Question 1.
[latex]\int_{\pi/2}^{\pi/2}[/latex]sin¹⁰ x dx
Solution:

Question 2.
[latex]\int_0^{\pi/2}[/latex]cos¹¹ x dx
Solution:

Question 3.
[latex]\int_0^{\pi/2}[/latex]cos⁷ x . sin²x dx.
Solution:

Question 4.
[latex]\int_0^{\pi/2}[/latex]sin⁴ x . cos⁴ x dx.
Solution:

Question 5.
[latex]\int_0^{\pi/2}[/latex]sin³ x cos⁶ x dx.
Solution:
[latex]\int_0^{\pi/2}[/latex]sin³ x cos⁶ x dx.
[latex]\int_0^{\pi/2}[/latex](1 – cos² x) cos⁶ x.sin x dx

Question 6.
[latex]\int_0^{2\pi}[/latex]sin² x cos⁴ x dx.
Solution:

Question 7.
[latex]\int_{-\pi/2}^{\pi/2}[/latex]sin² θ cos⁷ θ dθ.
Solution:
sin² θ cos⁷ θ is even function
f(θ) = sin² θ . cos⁷ θ dθ
f(-θ) = sin² (-θ) . cos⁷ (-θ)
= f(θ)
= 2[latex]\int_{-\pi/2}^{\pi/2}[/latex]sin² θ cos⁷ θ dθ

[latex]\int_0^{\pi/2}[/latex]sin^m x cosⁿx dx
n is odd n = 7

Question 8.
[latex]\int_{-\pi/2}^{\pi/2}[/latex]sin³ θ .cos³ θ dθ.
Solution:
f(θ) = sin³ θ . cos³ θ dθ
f(-θ) = sin³ (-θ) . cos³ (-θ)
= -sin³ θ cos³ θ = -f(θ)
f(θ) is odd
∴ [latex]\int_{-\pi/2}^{\pi/2}[/latex]sin³ θ.cos³ θ dθ = 0

Question 9.
[latex]\int_0^a[/latex]x(a² – x²)^7/2 dx
Solution:
x = a sin θ, a = a sin θ
dx = a cos θ dθ, θ = π/2
= [latex]\int_0^{\pi/2}[/latex]a sin θ(a² – a²sin²θ)^7/2 a cos θ dθ
= [latex]\int_0^{\pi/2}[/latex]a⁹ cos⁸ θ sin θ dθ
= a⁹[latex]\int_0^{\pi/2}[/latex]cos⁸ . θ sin θ dθ

Question 10.
[latex]\int_0^2[/latex]x^3/2.[latex]\sqrt{2-x}[/latex]dx
Solution:
x = 2 cos² θ
dx = 4 cos θ sin θ dθ

II. Evaluate the following integrals.

Question 1.
[latex]\int_0^1[/latex]x⁵(1 – x)^3/2 dx
Solution:
x = sin² θ
dx = 2 sin θ . cos θ . dθ

Question 2.
[latex]\int_0^4[/latex](16 – x²)^5/2 dx
Solution:

Question 3.
[latex]\int_{-3}^3[/latex](9 – x²)^3/2 x dx
Solution:
Let f(x) = (9 – x²)^3/2_x
f(x) = (9 – (-x²))^3/2(-x)
= (9 – x²)^3/2 . x
= -f(x)
∴ f is odd function
∴ [latex]\int_{-3}^3[/latex](9 – x²)^3/2 x dx = 0

Question 4.
[latex]\int_0^5[/latex]x³(25 + x²)^7/2 dx
Solution:
Let I = [latex]\int_0^5[/latex]x³(25 + x²)^7/2 dx
Put x = 5 sin θ
dx = 5 cosθ dθ

Question 5.
[latex]\int_{-\pi}^{\pi}[/latex]sin⁸ x cos⁷ x dx
Solution:
Let f(x) = sin⁸ x. cos⁷ x
f(-x) = sin⁸ (-x) . cos⁷ (-x)
= sin⁸ x. cos⁷ x
∴ f is even function.
∴ [latex]\int_{-\pi}^{\pi}[/latex]sin⁸ x cos⁷ x dx = 2[latex]\int_0^{\pi}[/latex]sin⁸ x cos⁷ x = 0

Question 6.
[latex]\int_3^7 \sqrt{\frac{7-x}{x-3}}[/latex]dx
Solution:
Put x = 3 cos²θ + 7 sin²θ
dx = (7 – 3)sin2θ dθ
dx = 4 sin 2θ dθ
U.L.
x = 3 cos²θ + 7 sin²θ
7 = 3 cos²θ + 7 sin²θ
4 cos²θ = 0
θ = [latex]\frac{\pi}{2}[/latex]
L.L
x = 3 cos²θ + 7 sin²θ
3 = 3 sin²θ + 7 sin²θ
4 sin²θ = 0
sinθ = 0
θ = 0
7 – x = 7 – (3 cos²θ + 7 sin²θ)
= (7 – 3)cos²θ
= 4 cos²θ
x – 3 = 3 cos²θ + 7 sin²θ – 3
= (7 – 3)sin²θ
= 4 sin²θ

Question 7.
[latex]\int_2^6\sqrt{(6-x)(x-2)}[/latex]dx
Solution:
Put x = 2 cos²θ + 6 sin²θ
dx = (6 – 2) sin2θ dθ
dx = 4 sin2θ dθ
U.L
x = 2 cos²θ + 6 sin²θ
6 = 2 cos²θ + 6 sin²θ
4 cos²θ = 0
cos θ = 0
θ = [latex]\frac{\pi}{2}[/latex]

L.L
x = 2 cos²θ + 6 sin²θ
2 = 2 cos²θ + 6 sin²θ
4 sin²θ = 0
θ = 0
6 – x = 6 – (2 cos²θ + 6 sin²θ)
= (6 – 2) cos²θ
= 4 cos²θ
x – 2 = 2 cos²θ + 6 sin²θ – 2
= (6 – 2)sin²θ
= 4 sin²θ

Question 8.
[latex]\int_0^{\pi}[/latex]tan⁵x cos⁸x dx
Solution:

III. Evaluate the following integrals.

Question 1.
[latex]\int_0^1[/latex]x^7/2 (1 – x)^5/2 dx
Solution:
Put x = sin²θ
dx = 2 sin θ cos θ dθ
U.L
x = sin²θ
1 = sin²θ
θ = [latex]\frac{\pi}{2}[/latex]

L.L
x = sin²θ
0 = sin²θ
θ = 0

Question 2.
[latex]\int_0^{\pi}[/latex](1 + cos x)³ dx
Solution:

Question 3.
[latex]\int_4^9\frac{dx}{\sqrt{(9 – x)(x – 4)}}[/latex]
Solution:
Put x = 4 cos²θ + 9 sin²θ
dx = (9 – 4)sin2θ dθ
dx = 5 sin2θ dθ

U.L
x = 4 cos²θ + 9 sin²θ
9 = 4 cos²θ + 9 sin²θ
5 cos²θ = 0
θ = [latex]\frac{\pi}{2}[/latex]

L.L
x = 4 cos²θ + 9 sin²θ
4 = 4 cos²θ + 9 sin²θ
5 sin²θ = 0
θ = 0

9 – x = 9 – (4 cos²θ + 9 sin²θ)
= (9 – 4) cos²θ
= 5 cos²θ

x – 4 = 4 cos²θ + 9 sin²θ – 4
= (9 – 4) sin²θ
= 5 sin²θ

Question 4.
[latex]\int_0^5[/latex]x²([latex]\sqrt{5-x}^7[/latex] dx
Solution:
Put x = 5 sin²θ
dx = 10 sinθ cosθ dθ

U.L
x = 5 sin²θ
5 = 5 sin²θ
sin²θ = 1
θ = [latex]\frac{\pi}{2}[/latex]

L.L
x = 5 sin²θ
0 = 5sin²θ
sin²θ = 0
θ = 0

Question 5.
[latex]\int_0^{2\pi}[/latex](1 + cos x)⁵(1 – cos x)³ dx.
Solution:
[latex]\int_0^{2\pi}[/latex](1 + cos x)⁵(1 – cos x)³ dx . (1 + cos x)³(1 + cos x)²(1 – cos x)³

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(b)

I. Evaluate the following definite integrals.

Question 1.
[latex]\int_0^a(a^2x-x^3) d x[/latex]
Solution:

Question 2.
[latex]\int_2^3 \frac{2 x}{1+x^2} d x[/latex]
Solution:
I = [ln|1 + x²|]³₂
= ln 10 – ln 5
= ln(10/5)
= ln 2

Question 3.
[latex]\int_0^\pi \sqrt{2+2 \cos \theta} d \theta[/latex]
Solution:

Question 4.
[latex]\int_0^\pi\sin^3x\cos^3xd x[/latex]
Solution:

Question 5.
[latex]\int_0^2|1-x|d x[/latex]
Solution:

Question 6.
[latex]\int_{-\pi / 2}^{\pi / 2} \frac{\cos x}{1+e^x} d x[/latex]
Solution:
[latex]\int_{-\pi / 2}^{\pi / 2} \frac{\cos x dx}{1+e^x}[/latex] ………….. (i)
cos x is even function
e^x is neither even nor odd.

Adding (i) and (ii) we get

Question 7.
[latex]\int_0^1\frac{dx}{\sqrt{3-2x}}[/latex]
Solution:
3 – 2x = t²
-2dx = 2t dt
dx = -t dt
3 – (2.1) = t²
1 = t²
3 – 2.0 = t²

Question 8.
[latex]\int_0^a(\sqrt{a}-\sqrt{x})^2[/latex]
Solution:

Question 9.
[latex]\int_0^{\pi / 4} \sec^4\theta d\theta[/latex]
Solution:
Let ∫sec⁴ θ dθ = [latex]\int_0^{\pi / 4} \sec^2\theta(1+\tan^2\theta)d\theta[/latex]
Put tan θ = y
sec² θ dθ = dy
θ = [latex]\frac{\pi}{4}[/latex] ⇒ y= 1
θ = 0 ⇒ y = 0
I = [latex]\int_0^a[/latex](1 + y²)dy = [y + [latex]\frac{y^3}{3}[/latex]]¹₀
= 1 + [latex]\frac{1}{3}=\frac{4}{3}[/latex]

Question 10.
[latex]\int_0^3\frac{x}{\sqrt{x^2+16}}[/latex]
Solution:

Question 11.
I = [latex]\int_0^1[/latex]x.e^-x²dx
Solution:
I = [latex]\int_0^a[/latex]x.e^-x²dx
⇒ -x² = t
⇒ -2x dx = dt
2x dx = -dt
x = 1 ⇒ t = 0
x = 0 ⇒ t = 1
I = [latex]\frac{1}{2}[/latex][latex]\int_0^a[/latex]-e^t dt
= [latex]\frac{1}{2}[/latex][-e^t]^-1₀
= [latex]\frac{1}{2}[/latex][e⁰ – e^-1]
= [latex]\frac{1}{2}[/latex](1 – [latex]\frac{1}{e}[/latex])

Question 12.
I = [latex]\int_1^5\frac{dx}{\sqrt{2x-1}}[/latex]
Solution:

II. Evaluate the following integrals:

Question 1.
I = [latex]\int_0^4\frac{x^2}{1+x}[/latex]
Solution:

Question 2.
[latex]\int_{-1}^2 \frac{x^2}{x^2+2}[/latex]
Solution:

Question 3.
I = [latex]\int_0^1 \frac{x^2}{x^2+2}[/latex]
Solution:

Question 4.
[latex]\int_0^{\pi / 2}[/latex]x² sin x dx
Solution:

Question 5.
[latex]\int_0^4[/latex]|2-x|dx
Solution:

Question 6.
[latex]\int_0^{\pi / 2}\frac{\sin^5 x}{\sin^5 x+\cos^5 x}[/latex]
Solution:

Question 7.
[latex]\int_0^{\pi / 2}\frac{\sin^2 x-\cos^2 x}{\sin^3 x+\cos^3 x}[/latex]dx
Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

III. Evaluate the following integrals :

Question 1.
[latex]\int_0^{\pi / 2}\frac{dx}{4+5\cos x}[/latex]
Solution:

Question 2.
[latex]\int_a^b\sqrt{(x-a)(b-x)}[/latex]dx
Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.
[latex]\int_0^a[/latex]x(a – x)ⁿdx
Solution:
I = [latex]\int_0^a[/latex]x(a – x)ⁿdx ………… (i)
[latex]\int_0^a[/latex]f(x) dx = [latex]\int_0^a[/latex]f(a – x)dx
I = [latex]\int_0^a[/latex](a – x).(x)ⁿdx ………… (ii)
I = [latex]\int_0^a[/latex]axⁿ dx – xⁿ⁺¹ dx

Question 7.
[latex]\int_0^2x\sqrt{2-x}[/latex]dx
Solution:
I = [latex]\int_0^2x.\sqrt{2-x}[/latex]dx
[latex]\int_0^2[/latex]f(x)dx = [latex]\int_0^2[/latex]f(a – x)dx
= [latex]\int_0^2[/latex](2 – x).√x dx
= [latex]\int_0^2[/latex]((2√x – x√x)) dx

Question 8.
[latex]\int_0^{\pi}[/latex]x sin³ x dx
Solution:

Question 9.
[latex]\int_0^{\pi}\frac{x}{1+\sin x}[/latex]dx
Solution:
[latex]\int_0^{\pi}\frac{x}{1+\sin x}[/latex]dx …………… (i)

Question 10.

Solution:

Question 11.
[latex]\int_0^1\frac{log(1+x)}{1+x^2}[/latex]dx
Solution:
Put x = tan θ
dx = sec² θ dθ
x = 0 ⇒ θ = 0
x = x ⇒ θ = [latex]\frac{\pi}{4}[/latex]

Question 12.
[latex]\int_0^{\pi}\frac{x \sin x}{1+\cos^2 x}[/latex]dx
Solution:

Question 13.
[latex]\int_0^{\pi/2}\frac{\sin^2 x}{\cos x+\sin x}[/latex]dx
Solution:

Question 14.
[latex]\int_0^{\pi}\frac{1}{3+2\cos x}[/latex]dx
Solution:

Question 15.
[latex]\int_0^{\pi/4}[/latex]log(1 + tan x)dx
Solution:

Question 16.
[latex]\int_{-1}^{3/2}[/latex]|x sin πx| dx
Solution:
We know that |x. sin πx| = x . sin πx
where -1 ≤ x ≤ 1
and |x . sin πx| = – x.sin πx where 1 < x ≤ 3/2

Question 17.
[latex]\int_0^1sin^{-1}\frac{2x}{1+x^2}[/latex]dx
Solution:
[latex]\int_0^1sin^{-1}\frac{2x}{1+x^2}[/latex]dx
Put x = tan θ ⇒ dx = sec² θ dθ
x = 0 ⇒ θ = 0
x = 1 ⇒ θ π/4

Question 18.
[latex]\int_0^1[/latex]x tan^-1x dx
Solution:
[latex]\int_0^1[/latex]x. tan^-1x dx
Put x = tan θ ⇒ dx = sec² θ dθ
x = 0 ⇒ θ = 0;

Question 19.
[latex]\int_0^{\pi}\frac{x\sin x}{1+\cos^2 x}[/latex]dx
Solution:

Question 20.
Suppose that f : R → R is continuous periodic function and T is the period of it. Let a ∈ R. Then prove that for any positive integer n,

Solution:

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(a)

I. Evaluate the following integrals as the limit of a sum.

Question 1.
[latex]\int_0^5(x+1) d x[/latex]
Solution:

Question 2.
[latex]\int_0^4(x^2+1) d x[/latex]
Solution:

II. Evaluate the following integrals as limit of a sum.

Question 1.
[latex]\int_0^4(x+e^{2x}) d x[/latex]
Solution:

Question 2.
[latex]\int_0^1(x-x^2) d x[/latex]
Solution: