Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a)
I.
Question 1.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = cex – be-x + x².
Solution:
Given equation is xy = cex – be-x + x²
Differentiating w.r.to x, we get
xy1 + y = cex – be-x + 2x.
Again differentiating w.r.to x, we get
xy2 + y1 + y1 = cex – be-x + 2
xy2 + 2y2 = xy – x² + 2
Arbitary constants a and b are eliminated.
∴ The order is 2.
Question 2.
Find the order of the differential equation of the family of all circles with their centres at the origin.
Solution:
Equation of the circle with centre at origin is x² + y² = r²
Order = no .of arbitrary constants = 1
![]()
II.
Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets.
i) y = c(x – c)² ; (c)
Solution:
y = c(x – c)² ………….. (1)
Differentiating w.r. to x
y1 = c. 2(x – c) ………….. (1)
Dividing (2) by (1)
\(\frac{y_2}{y}=\frac{2c(x-c)}{c(x-c)^2}\)
x – c = \(\frac{2y}{y_1}\)
c = x – \(\frac{2y}{y_1}\)
Substituting in (1)
y = x – \(\frac{2y}{y_1}\)(x – \(\frac{2y}{y_1}\))²
= \(\frac{xy_1-2y}{y_1}.\frac{4y^2}{y_1^2}\)
y.y³1 = 4y²(xy1 – 2y)
i.e., y³1 = 4y (xy1 – 2y)
= 4xyy1 – 8y²
(\(\frac{dy}{dx}\))³ – 4xy\(\frac{dy}{dx}\) + 8y² = 0
ii) xy = aex + be-x; (a, b)
Solution:
xy = aex + b.e-x
Differentiating w.r.t. x
x . y1 + y = aex – b . e-x
Differentiating again w.r.t. x
xy2 + y1 + y1 = aex + be-x = xy
\(\frac{d^2y}{dx^2}\) + 2\(\frac{dy}{dx}\) – xy = 0
iii) y = (a + bx)ekx ; (a, b)
Solution:
y = (a + bx)ekx
Differentiating w.r.t. x
y1 = (a + bx) ekx. k + ekx . b
= k . y + b.ekx
y1 – ky = b.ekx …………. (1)
Differentiating again w.r.t. x
y2 – ky1 = kb ekx
= k(y1 – ky) ………… (2)
= ky1 – k²y
\(\frac{d^2y}{dx^2}\) – 2k\(\frac{dy}{dx}\) + k²y = 0
iv) y = a cos (nx + b); (a, b)
Solution:
y = a cos (nx + b)
y1 = – a sin (nx + b) n
y2 = – an. cos (nx + b) n
= – n² . y
\(\frac{d^2y}{dx^2}\)+n².y = 0
![]()
Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The rectangular hyperbolas which have the co-ordinate axes as asymptotes.
Solution:
Equation of the rectangular hyperbolas is xy = c² where c is arbitrary constant
Differentiating w.r.t. x
x\(\frac{dy}{dx}\) + y = 0
ii) The ellipses with centres at the origin and having co-ordinate axes as axes.
Solution:
Equation of ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Differentiating w.r.to ‘x’ we get
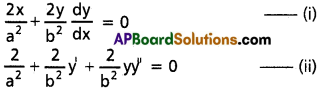
Multiply (ii) by x and subtract from (i)
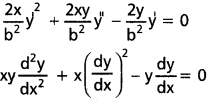
III.
Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets :
i) y = ae3x + be3x; (a, b)
Solution:
Differentiating w.r. to x
y1 = 3ae3x + 4be4x
y1 – 3a. e3x = 4b.e4x
= 4(y – a. e3x)
= 4y – 4a. e3x
y1 – 4y = – a.e3x ………… (1)
Differentiating again w.r.t. x
y2 – 4y1 = – 3a. e3x
= 3 (y1 – 4y) by (1)
= 3y1 – 12y
\(\frac{d^2y}{dx^2}\) – 7\(\frac{dy}{dx}\) + 12y = 0
ii) y = ax² + bx; (a, b)
Solution:

Adding all three equations we get
x²\(\frac{d^2y}{dx^2}\) – 2x\(\frac{dy}{dx}\) + 2y = 0
iii) ax² + by² = 1; (a, b)
Solution:
ax² + by² = 1
by² = 1 – ax² ………….. (1)
Differentiating w.r.t. x
2by. y1 = – 2ax ………….. (2)
Dividing (2) by (1)
\(\frac{by.y_1}{by^2}=\frac{-ax}{1-ax^2}\)
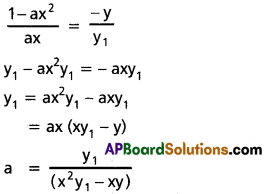
Differentiating w.r.t. x

iv) xy = ax² + \(\frac{b}{x}\); (a, b)
Solution:
xy = ax² + \(\frac{b}{x}\)
x²y = ax³ + b
Differentiating w.r.t. x
x²y1 + 2xy = 3ax²
Dividing with x
xy1 + 2y = 3ax ………… (1)
Differentiating w.r.t. x
xy2 + y1 + 2y1 = 3a
xy2 + 3y1 = 3a ………… (2)
Dividing (1) by (2)
\(\frac{xy_1+2y}{xy_2+3y_1}=\frac{3ax}{3a}=x\)
Cross multiplying
xy1 + 2y = x²y2 + 3xy
x²y2 + 2xy1 – 2y = 0
x²\(\frac{d^2y}{dx^2}\) + 2x\(\frac{dy}{dx}\) – 2y = 0
Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The circles which touch the Y – axis at the origin.
Solution:
Equation of the required circle is
x² + y² + 2gx = 0
x² + y² = – 2gx …………. (1)
Differentiating w.r. t x
2x + 2yy1 = – 2g ……….. (2)
Substituting in (1)
x² + y² = x(2x + 2yy1) by (2)
= 2x² + 2xyy1
yy² – 2xyy1 – 2x² = 0
y² – x² = 2xy\(\frac{dy}{dx}\)
ii) The parabolas each of which has a latus rectum 4a and whose axes are parallel to X – axis.
Solution:
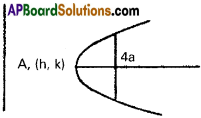
Equation of the required parabola is
(y – k)² = 4a (x – h) …………. (1)
Differentiating w.r.t. x
2(y – k)y1 = 4a …………. (2)
Differentiating w.r.t. x
(y – k) y2 + y²1 = 0 …………. (3)
From (2), y – k = \(\frac{2a}{y_1}\)
Substituting in (3)
\(\frac{2a}{y_1}\).y2 = y²1 = 0
2ay2 + y³1 = 0
![]()
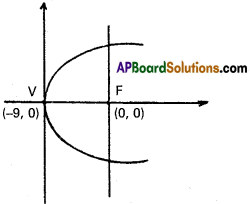
iii) The parabolas having their foci at the origin and axis along the X – axis.
Solution:
Equation of parabola be y² = 4a(x + a)