Mahesh

Students can go through AP Board 7th Class Maths Notes Chapter 15 Symmetry to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 15 Symmetry

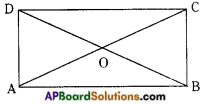
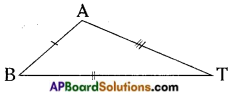
→ Line of symmetry: The line which divides a figure into two identical parts is called the line of symmetry or axis of symmetry.
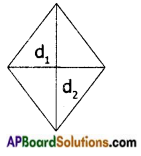
Ex: In the adjacent figure the dotted lines are the line of symmetry.

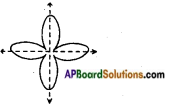
→ An object can have one or more than one lines of symmetry or axes of symmetry.
Ex: In the above figure there are two lines of symmetry.

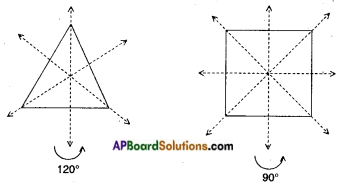
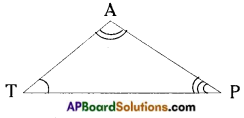
→ If we rotate a figure, about a fixed point by a certain angle and the figure looks exactly the same as before, we say that the figure has rotational symmetry.
Ex: An equilateral triangle; a square etc.

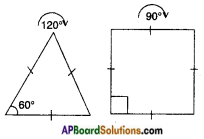
→ The angle of turning during rotation is called the angle of rotation (or) the minimum angle rotation of a figure to get exactly the same figure as original is called the angle of rotation.
Ex: i) Angle of rotation of an equilateral triangle = 120°.
ii) Angle of rotation of a square = 90°.

→ All figures having rotational symmetry of order 1, can be rotated completely through 360° to come back to their original position. So we say that an object has rotational symmetry only when the order of symmetry is more than 1.
Eg: The order of rotational symmetry for an equilateral triangle is 3.
ii) For a square is 4.

→ Some shapes only have line symmetry and some have only rotational symmetry and some have both. Squares, equilateral triangles and circles have both line symmetry and rotational symmetry.

Students can go through AP Board 7th Class Maths Notes Chapter 14 Understanding 3D and 2D Shapes to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 14 Understanding 3D and 2D Shapes

→ A net is a sort of skeleton – outline in 2-D, which, when folded, results in a 3-D shape. Each shape can also have more than one net according to the way we cut it.
Eg:

→ 3-D shapes can be visualised by drawing their nets on 2-D surfaces.

→ Oblique sketches are drawn on a grid paper to visualise 3-D shapes.

→ Isometric sketches can be drawn on a dot isometric paper to visualise 3-D shapes.

Students can go through AP Board 7th Class Maths Notes Chapter 13 Area and Perimeter to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 13 Area and Perimeter

→ The area of a parallelogram is equal to the product of its base (b) and corresponding height (h) A = bh.

Any side of the parallelogram can be taken as its base.

→ The area of a triangle is equal to half the product of its base and height.

A = [latex]\frac{1}{2}[/latex] bh
A triangle = Half a parallelogram

→ The area of a Rhombus is equal to half the product of Its diagonals.

A = [latex]\frac{1}{2}[/latex] d₁d₂

→ The circumference of a circle = 2πr = πd where π = [latex]\frac{22}{7}[/latex] or 3.14, d = [latex]\frac{r}{2}[/latex]

Students can go through AP Board 7th Class Maths Notes Chapter 12 Quadrilaterals to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 12 Quadrilaterals

→ Quadrilateral: A closed figure bounded by four line segments is called a quadrilateral.
In the figure, ABCD is a quadrilateral.

→ A quadrilateral divides a plane into three parts.
i) Interior of the quadrilateral
ii) Exterior of the quadrilateral
iii) Boundary of the quadrilateral

→ In the figure the points P, Q are in the interior of the quadrilateral. i3r In the figure the points R, S are in the exterior of the quadrilateral.

→ In the figure the points A, B, C, D are on the boundary of the quadrilateral.

→ A quadrilateral is said to be a convex quadrilateral if all line segments joining points in the interior of it also lie in its interior completely.
□ BELT is a convex quadrilateral.

→ A quadrilateral is said to be a concave quadrilateral if all line segments joining points in the interior of it do not necessarily lie in its interior completely.

In □ RING, the line segment [latex]\overline{\mathrm{AB}}[/latex] does not lie completely in its interior, as such the quadrilateral RING is a concave quadrilateral.

→ Sum of the interior angles of a quadrilateral is 360°.
∠A + ∠B + ∠C + ∠D = 360°

→ A quadrilateral in which one pair of opposite sides are parallel is called a trapezium.
In □ ABCD ; AB // CD

→ A kite has four sides. There are exactly two distinct pairs of equal length.
In quadrilateral KITE,

KI = KE and IT = ET

→ A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram. In quadrilateral ABCD,
AB // CD and AD // BC. Hence □ ABCD is a parallelogram.

→ In a parallelogram,

• Opposite sides are parallel and equal [AB = CD and AD = BC]
• Diagonals bisect each other (AO = OC and BO = OD)
• Opposite angles are equal (∠A = ∠C and ∠B = ∠D)
• Adjacent angles are supplementary (∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180°)

→ A parallelogram in which adjaœnt sides are equal is called a Rhombus.
In quadrilateral ABCD,
AB = BC = CD = DA and hence □ ABCD is a Rhombus.

In a rhombus diagonals bisect each other at right angles,
(i.e.) AC ⊥ BD and AO = OC, BO = OD

→ A rectangle is a parallelogram with equal angles (OR)
A parallelogram in which one angle is a right angle is called a rectangle.

In fig. ∠A = ∠B = ∠C = ∠D = 90° and □ ABCD is a rectangle.
In a rectangle the diagonals are equal.
In a rectangle the diagonals bisect each other.

(AC = BD and AO = OC; BO = OD)

→ A square is a rectangle with equal adjacent sides.

In the figure AB = BC = CD = DA
∠A = ∠B = ∠C = ∠D = 90°
In a square the diagonals are equal and bisect at right angles. Also they are equal.
[(AO = OC ; BO = OD), (AC ⊥ BD) and (AC = BD)]

Flow chart of family of quadrilaterals

Students can go through AP Board 7th Class Maths Notes Chapter 11 Exponents to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 11 Exponents

→ Very large numbers are easier to read, write and understand when expressed in exponential form.
Eg : 10000 = 10⁴
8 × 8 × 8 × 8 × 8 × ….. × 8 (16 times) = 8¹⁶.

→ When a number is multiplied by itself for many number of times (repeated multiplication) then we write it in exponential form.
Eg : 2 × 2 × 2 × 2 = 2⁴ Here 2 is base 4 is exponent.
3 × 3 × 3 × 3 × 3 = 3⁵ Here 3 is base 5 is exponent.

→ a . a . a . a ….. a (m times) = a^m.

→ Here ‘a’ is called the base and ‘m’ is called the exponent.

→ Laws of exponents

i) a^m × aⁿ = a^m+n

ii)  (a^m)ⁿ = a^mn

iii) (ab)^m = a^m . b^m

iv) a^m = aⁿ ⇒ m = n

v) a^-n = [latex]\frac{1}{a^{n}}[/latex]

vi) [latex]\frac{\mathrm{a}^{\mathrm{m}}}{\mathrm{a}^{\mathrm{n}}}[/latex] = a^m-n  if (m > n)
= [latex]\frac{1}{a^{n-m}}[/latex]  if (m < n)
= 1 if (m = n)

vii) [latex]\left(\frac{a}{b}\right)^{m}[/latex] = [latex]\frac{a^{m}}{b^{m}}[/latex]

viii) a⁰ = 1 where a ≠ 0

Students can go through AP Board 7th Class Maths Notes Chapter 10 Algebraic Expressions to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 10 Algebraic Expressions

→ Variable: It takes different values.
Ex: x, y, z, a, b, c, m etc.
Constant: The value of constant is fixed.
Ex: 1, 2, [latex]\frac{-2}{3}[/latex], [latex]\frac{4}{5}[/latex] etc.

→ Algebraic Expression: An algebraic expression is a single term or a combination of terms connected by the symbols ‘+’ (plus) or(minus).
Ex: 2x + 3, [latex]\frac{2}{5}[/latex]p, 3x – 1 etc.

→ Numerical Expression : If every term of an expression is a constant term, then the expression is called a Numerical expression.
Ex: 2 + 1, -5 × 3, (12 + 4) ÷ 3.
Note: In the expression 2x + 9, ‘2x’ is an algebraic term. ‘9’ is called numeric term.

→ Like terms are terms which contain the same variables with the same exponents.
Ex: 12x, 25x, -7x are like terms.
2xy², 3xy², 7xy² are like terms.

→ Coefficient: In a.xⁿ, ‘a’ is called the numerical coefficient and ‘x’ is called the literal coefficient.
Types of algebraic expressions.

→ Degree of a monomial: The sum of all exponents of the variables present in a monomial is called the degree of the term or degree of the monomial.
Ex: The degree of 9x²y² is 4 [∵ 2 + 2 = 4]
Note: Degree of constant term is zero.
The highest of the degrees of all the terms of an expression is called the degree of the expression.
Ex: The degree of the expression ax + bx² + cx³ + dx⁴ + ex⁵ is 5.

→ The difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.
Note:

1. If no two terms of an expression are alike then it is said to be in the simplified form.
2. In an expression, if the terms are arranged in such a way that the degrees of the terms are in descending order then the expression is said to be in standard form.
3. Addition (or) subtraction of expressions should be done in two methods, they are
   i) Column or Vertical method.
   ii) Row or Horizontal method.

Students can go through AP Board 7th Class Maths Notes Chapter 9 Construction of Triangles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 9 Construction of Triangles

→ A triangle can be drawn of any three of its elements are known.

→ To construct a triangle, we need

1. Three sides
2. Any two sides and the angle included between them.
3. Two angles and the side included between them.
4. Hypotenuse and one adjacent side of a right angled triangle.
5. Two sides and a non-included angle.

Students can go through AP Board 7th Class Maths Notes Chapter 8 Congruency of Triangles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 8 Congruency of Triangles

→ Two figures are said to be identical if their shapes are same.
Eg: Any two squares, circles or equilateral triangles.

→ Two figures are said to be congruent if they are identical in shape and equal in size.

→ Two line segments are congruent if they have same lengths.

→ Two triangles are congruent if the corresponding angles are equal.

→ We establish the congruency of the triangles by following criteria.

→ S.S.S. criterion: If three sides of a triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.

FA = TI; AN = IN; FN = TN then △FAN ≅ △TIN

→ S.A.S. criterion: If two sides and the angle included between the two sides of a triangle are equal to the corresponding two sides and the included angle of another triangle, then the two triangles are congruent.

CA = PI; ∠C = ∠P; CT = PG
then, △CAT ≅ △PIG

→ A.S.A. criterion : If two angles and the included side of a triangle are equal to the corresponding two angles and included side of another triangle then the triangles are congruent.

∠A = ∠I; AT = IM; ∠T = ∠M then △MAT ≅ △DIM.

→ R.H.S. criterion: In two right angled triangles, if the hypotenuse and one corresponding side are equal then they are congruent.

∠B = ∠E = 90°
BC = EF
AC = DF
then △ABC ≅ △DEF

→ If by any criterion two triangles are congruent then all the corresponding parts are equal.

Students can go through AP Board 7th Class Maths Notes Chapter 7 Data Handling to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 7 Data Handling

→ Data: Information which is in the form of numbers or words and helps in taking decisions or drawing conclusions is called data. Tables and graphs are the ways in which data is presented.
The numerical entries in the data are called ‘observations’.

→ The average or Arithmetic Mean or Mean
A.M = [latex]\frac{\text { Sum of all observations }}{\text { Number of observations }}[/latex]

→ (i.e.,) A.M. is equal to sum of all the observations of a data set divided by the number of observations. It lies between the lowest and highest values of the data.

→ Mode: An observation of data that occurs most frequently is called the mode of the data. A data may have one or more modes and sometimes none.

→ Median: Median is simply the middle observation, when all observations are arranged in ascending or descending order. In case of even number of observations median is the average of middle observations.

→ Mean, mode, median are representative values for a data set.

→ When all values of data set are increased or decreased by a certain number, the mean also increases or decreases by the same number.

→ Data can be presented in bar graphs / double bar graphs or pie chart.

→ Bar graph: Bar graph are made up of bars of uniform width which can be drawn horizontally or vertically with equal spacing between them. The length of each bar tells us the frequency of the particular item. We take convenient scale for the length of bar graph.

→ Double bar graph: It presents two observations side by side.

→ Pie chart: A circle is divided into sectors to represent the given data.
Angle subtended by the sector at the centre of the circle is directly proportional to each observation.

Students can go through AP Board 7th Class Maths Notes Chapter 6 Ratio – Applications to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 6 Ratio – Applications

→ Ratio: A ratio is an ordered comparison of quantities of the same units.
We use the symbol ‘:’ to represent a ratio. The ratio of two quantities ‘a’ and ‘b’ is a : b and we read it as “a is to b”. The two quantities ‘a’ and ‘b’ are called the terms of the ratio. The first quantity ‘a’ is called first term or antecedent and the second quantity ‘b’ is called consequent.

→ Proportion: If two ratios are equal, then the four terms of the ratios are said to be in proportion. We use the symbol : : (is as)
If two ratios a : b and c : d are equal, we write a : b :: c : d or a : b = c : d
Here ‘a’, ‘d’ are called extremes and b, c are called means.

→ Unitary Method: The method in which we first find the value of one unit and then the value of the required number of units is known as unitary method.
Eg: If the cost of 5 pens is Rs. 85; then the cost of 12 pens is ……… ?
Solution. Cost of 5 pens = Rs. 85
Cost of 1 pen = [latex]\frac{85}{5}[/latex] = Rs. 17
∴ Cost of 12 pens = 12 × 17 = Rs. 204

→ Direct proportion: If in two quantities, when one quantity increases, the other also increase or vice-versa then the two quantities are said to be in direct proportion.
Eg: The number of books and their cost are in direct proportion.
As the number of books increases, the cost also increases.

→ Ratios also appear in the form of percentages.

→ The word percent means “per every hundred” or for a hundred. The symbol % is used to denote percentage.

→ To convert a quantity into its equivalent percentage

• express it as a fraction.
• multiply it with 100.
• assign % symbol.

Eg: A man purchased an article for Rs. 80 and sells it for Rs. 100. Find his gain percent.
Solution. Cost price = Rs. 80
Selling price = Rs. 100
gain = Rs. 20
gain as a fraction = [latex]\frac{20}{80}[/latex]
gain as percent = [latex]\frac{20}{80}[/latex] × 100 = 25%

→ When C.P > S.P there incurs loss.

→ When C.P < S.P there is gain.

→ When C.P = S.P neither loss nor gain.

→ Loss = C.P – S.P gain = S.P – C.P

→ Discount is always expressed as some percentage of marked price.

→ In general when P is principle; R% is rate of interest per annum and I is the interest, then
I = R% of P
I = R% of P for T years

Students can go through AP Board 7th Class Maths Notes Chapter 5 Triangle and Its Properties to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 5 Triangle and Its Properties

→ Triangles can be classified according to properties of their sides and angles. Based on sides, triangles are of three types.

→ Equilateral triangle: A triangle in which all the three sides are equal is called an equilateral triangle. In △ABC
AB = BC = CA, also ∠A = ∠B = ∠C In an equilateral triangle each angle is equal to 60°.

→ Isosceles triangle: A triangle in which two sides are equal is called an isosceles triangle.
In △PQR
PQ = PR also ∠Q = ∠R

The non-equal side in an isosceles triangle may be taken as base of the triangle.

→ Scalene triangle: A triangle in which no two sides are equal is called a scalene triangle.

In △BAT
BA ≠ AT ≠ BT also ∠B ≠ ∠A ≠ ∠T.

→ Based on angles, triangles can be classified into three types.

→ Acute angled triangle: A triangle in which all the three angles are acute is called an acute-angled triangle.

In △TAP,
∠T, ∠A, ∠P are acute angles.

→ Obtuse angled triangle: A triangle in which one angle is obtuse is called an obtuse angled triangle.

In △FAN,
∠A is obtuse angle.
A triangle cannot have more than one obtuse angle,

→ Right angled triangle: A triangle in which one angle is a right angle is called a right angled triangle.

In △COT
ZO is right angle (i.e) 90°.
A triangle cannot have more than one right angle,

→ Right angled isosceles triangle: A triangle in which one angle is right angle and two sides are equal is called a right angled isosceles triangle.

In △POT,
PO = OT and ∠O = 90° also
∠P = ∠T = 45°

→ Family of triangles – Flow chart

→ Relation between sides of a triangle
In any triangle the sum of the lengths of any two sides is greater than the length of the third side.

In △TIN,
TI + IN > TN; TN + NI > TI; TI + TN > IN
Also the difference between lengths of any two sides of the triangle is less than the length of the third side.
In △TIN, TI > TN – NI; IN > TI – TN; TN > IN – TI

→ Altitutes of a triangle
The length of a line segment drawn from a vertex to its opposite side and is perpendicular to it is called an altitude or height of the triangle. An altitude can be drawn from each vertex.

Altitude of a triangle may be in its interior or exterior.

→ Medians of a triangle
A line segment joining a vertex and the mid-point of its opposite side is called a median.

A triangle has three medians.
The medians of a triangle are concurrent.
The point of concurrence of medians of a triangle is called the centroid of the triangle.
In △ABC, D, E and F are mid-points of the sides AB, BC and AC.
AE, CD and BF are mid-points.
G is the centroid.

→ Angle – sum property of a triangle: The sum of interior angles of a triangle is equal to 180° or two right angles.

In △BET,
∠B + ∠E + ∠T = 180°

→ Exterior angle of a triangle

→ When one side of a triangle is produced, the angle thus formed is called an exterior angle.

In △COL; the side OL is produced to D.
∠CLD is an exterior angle.
The exterior angle of a triangle is equal to the sum of the interior opposite angles.
∠COL + ∠OCL = ∠CLD

Students can go through AP Board 7th Class Maths Notes Chapter 4 Lines and Angles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 4 Lines and Angles

→ Complementary angles: If the sum of two angles is 90°, the angles are called complementary angles.
Eg: 55°, 35° are complementary angles.

→ Linear pair of angles: When a ray stands on a line, the pair of angles thus formed are called linear pair of angles and their sum is 180°. In the figure ∠x and ∠y are called linear pair of angles.

→ Adjacent angles: Two angles with a common vertex and a common arm are called adjacent angles. Here the non-common arms lie on either sides of the common arm.
Eg: ∠AOB and ∠BOC are adjacent angles.

→ Supplementary angles : Two angles are said to be supplementary if their sum is 180°. Eg : (100°, 80°), (110°, 70°), (60°, 120°)

→ Vertically opposite angles: Two angles are said to be vertically opposite angles if they are formed by two intersecting lines and are not adjacent.
Eg: ∠AOC and ∠BOD are vertically opposite angles.

→ A line which intersects two or more lines at distinct points is called a transversal. In the figures ‘t’ is a transversal.

In the figure (i) t is not a transversal as it doesn’t intersect other two lines at two distinct points.

→ When a transversal intersects a pair of lines, 8 angles are formed.
Here l, m are two lines and ‘t’ is a transversal.

The angles are ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.
∠3, ∠4, ∠5, ∠6 are called interior angles and ∠1, ∠2, ∠7 and ∠8 are called exterior angles.

→ When a transversal intersects a pair of lines the following pairs of angles are called corresponding angles.

i) One angle is interior and the other is exterior.
ii) Not adjacent angles.
iii) Two angles are on the same side of the transversal.

→ The following pairs are called alternate interior angles
i) both are interior
ii) not-adjacent
iii) either sides of the transversal

→ The following pairs are called alternate exterior angles
i) both are exterior
ii) not-adjacent
iii) on the either sides of the transversal

→ The following pairs are called interior angles on the same side of the transversal.

→ When a pair of parallel lines intersected by a transversal the pairs of corresponding angles are equal.
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 = ∠8

The pairs of alternate interior angles are equal.
∠3 = ∠5
∠4 = ∠6
The pairs of alternate exterior angles are equal.
∠1 = ∠7
∠2 = ∠8
The interior angles on the same side of the transversal are supplementary.
∠3 + ∠6 = 180°
∠4 + ∠5 = 180°
The exterior angles on the same side of the transversal are supplementary.
∠1 + ∠8 = ∠2 + ∠7 = 180°

→ Conversely when a transversal intersects a pair of lines in such way
i) making pairs of corresponding angles equal
(or)
ii) making alternate interior angles equal.
(or)
iii) making alternate exterior angles equal.
(or)
iv) making angles on the same side of the transversal interior/exterior supplementary then the lines are parallel.