Category: Class 8

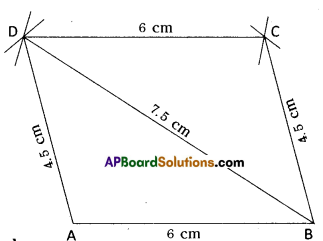
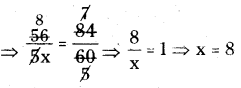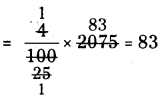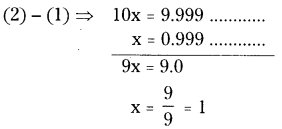AP State Syllabus AP Board 8th Class Maths Solutions Chapter 5 Comparing Quantities Using Proportion Ex 5.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson Comparing Quantities Using Proportion Exercise 5.2

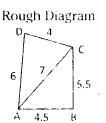
Question 1.
In the year 2012, it was estimated that there were 36.4 crore Internet users worldwide. In
the next ten years, that number will be increased by 125%. Estimate the number of Internet
users worldwide in 2022.
Solution:
Internet users in the year 2012
= 36.4 crores.
The number will be increased by next
10 years = 125%
∴ The no. of internet users in the year 2022
= 36.4 + 125% of 36.4
= 36.4 + [latex]\frac { 125 }{ 100 }[/latex] × 36.4
= 36.4 + 45.5
= 81.9 crores.

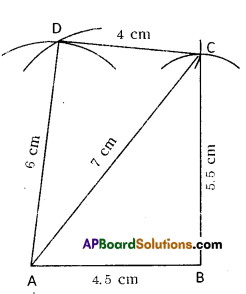
Question 2.
A owner increases the rent of his house by 5% at the end of each year. If currently its rent is ₹ 2500 per month, how much will be the rent after 2 years’?
Solution:
Present house rent = ₹ 2500 If the owner increases the rent by 5% on every year then the rent of the house after 2 years

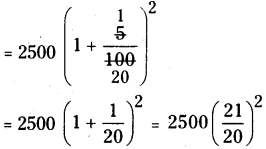
= 2500 × [latex]\frac { 21 }{ 20 }[/latex] x [latex]\frac { 21 }{ 20 }[/latex]
= ₹ 2756.25

Question 3.
On Monday, the value of a company’s shares was ₹ 7.50. The price increased by 6% on Tuesday, decreased by 1.5% on Wednesday, and decreased by 2% on Thursday. Find the value of each share when trade opened on Friday.
Solution:
The value of the share when trade opened on Friday
= ₹ 7.674

Question 4.
With most of the Xerox machines. you can reduce or enlarge your original by entering a percentage for the copy. Reshma wanted to enlarge a 2 cm by 4 cm drawing. She set the Xerox machine for 150% and copied her drawing. What will be the dimensions of the
copy of the drawing be’?
Solution:
Length of the copy = 2 cm
breadth = 4 cm
If the length is increase in 150% then its
measure = 150 % of 2 cm
= [latex]\frac { 150 }{ 100 }[/latex] × 2 = 1.5 × 2 = 3 cm

If the breadth is increase in 150% then
its measure = 150 % of 4 cm 150
= [latex]\frac { 150 }{ 100 }[/latex] × 4 = 1.5 × 4 = 6 cm
100
∴ New length = 3 cm
breadth = 6 cm

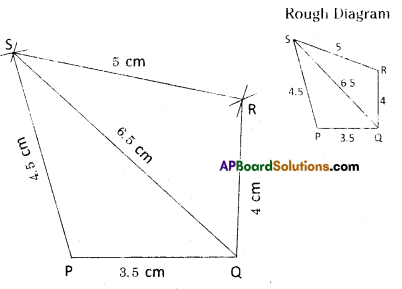
Question 5.
The printed price of a book is ₹ 150. And discount is 15%. Find the actual amount to be paid.
Solution:
The printed price of a book = ₹ 150
Discount % = 15%
∴ Discount = 15% of 150
= [latex]\frac { 15 }{ 100 }[/latex] × 150 = ₹22.5
∴ The C.P. of a book = 150 – 22.5
= ₹127.50/-

Question 6.
The marked price of an gift item is ₹ 176 and sold it for ₹ 165. Find the discount percent.
Solution:
Marked price of a gift = ₹176
S.P. = 165
Discount = 176 – 165 = ₹ 11

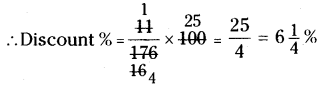
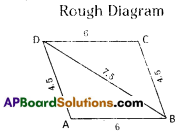
Question 7.
A shop keeper purchased 200 bulbs for ₹10 each. However 5 bulbs were fused and put
them into scrap. The remaining were sold at ₹12 each. Find the gain or loss percent.
Solution:
The C.P. of 200 bulbs at the rate of ₹10 for each = 200 × 10 = ₹ 2000
If 5 bulbs are fused then remaining are
= 200 – 5 = 195
∴ TheS.P. of 195 bulbs at the rate of ₹12 for each = 195 × 12 = ₹ 2340
∴ S.P. > C.P.
∴ Profit = S.P.-C.P.
= 2340 – 2000 = 340
Profit = [latex]\frac { Profit }{ C.P }[/latex] × 100 = [latex]\frac { 340 }{ 2000 }[/latex] × 100
Profit = 17%

Question 8.
Complete the following table with appropriate entries (Wherever possible)

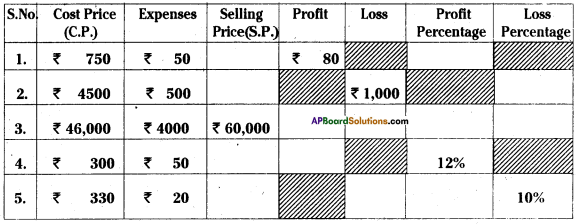
Solution:

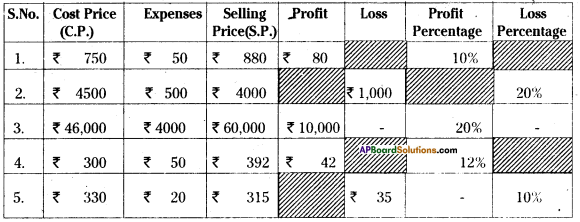
Question 9.
A table was sold for ₹2,142 at a gain of 5%. At what price should it be sold to gain 10%.
Solution:
S.P. of a table = ₹ 2142
Profit = 5%

∴ The C.P. of buyyer = ₹ 2040
Profit % = 10%

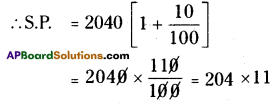
∴ S.P. = ₹2244

Question 10.
Gopi sold a watch to Ibrahim at 12% gain and Ibrahim sold it to John at a loss of 5%. If John paid ₹1,330, then find how much did Gopi sold it?
Solution:
. Let Gopi’s cost price = ₹100
Gain = 12%
∴ Gopi’s selling price to Ibrahim or Ibrahim’s cost price = ₹100 + ₹12 = ₹112
∴ Ibrahim’s loss = 5%
∴ Ibrahim’s selling price =
[latex]112\left(\frac{100-5}{100}\right)=\frac{112 \times 95}{100}[/latex] = ₹106.40
For ₹100 we get = ₹106.40
For ₹1330 how much we get ?

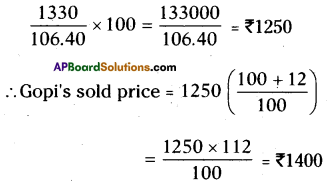
Question 11.
Madhu and Kavitha purchased a new house for ₹3,20,000. Due to some economic
problems they sold the house for ₹2,80,000. Find (a) The loss incurred (b) the loss percentage.
Solution:
C.P. of a house = ₹ 3,20,000
S.P. of a house = ₹ 2,80,000
∴ C.P. > S.P.
a) Loss
= C.P. – S.P.
= 3,20,000 – 2,80,000 = 40,000

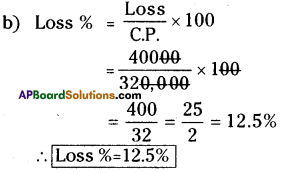
Question 12.
A pre-owned car show-room owner bought a second hand car for ₹ 1,50,000. He spent ₹20,000 on repairs and painting, then sold it for ₹ 2,00,000. Find whether he gets profit or loss. If so, what percent?
Solution:
After repair, the C.P of a car
= 1,50,000 + 20,000 = 1,70,000
S.P. of a ear = ₹ 2,00,000
∴ S.P. > C.P.
∴ Profit = S.P.-C.P.
= 2,00,000-1,70,000= 30,000
Profit = [latex]\frac { Profit }{ C.P }[/latex] × 100
[latex]\frac { 30,000 }{ 1,70,000 }[/latex] × 100 = Profit = [latex]\frac { 300 }{ 17 }[/latex]
Profit% = 17.64%

Question 13.
Lalitha took a parcel from a hotel to celebrate her birthday with her friends. It was billed with ₹ 1,450 including 5% VAT. Lalitha asked for some discount, the hotel owner gave 8% discount on the bill amount. Now find the actual amount that lalitha has to pay to the hotel owner
Solution:
After allowing 5% VAT, the total bill = ₹ 1450
If 8% discount is allowed on bill, then
Discount = 8% of 1450
[latex]\frac { 8 }{ 100}[/latex] × 1450 = ₹116
Discount = ₹116
∴ Lalitha has to pay the bill = 1450 -116
= ₹ 1334

Question 14.
If VAT is included in the price, find the original price of each of the following.

Solution:

Question 15.
Find the buying price of each of the following items when a sales tax of 5% is added on them.
(1) a towel of ₹50 (ii) Two bars of soap at ₹35 each.
Solution:
Given that Sales tax = 5%
(i) Cost of a towel = ₹ 50
Sales Tax = 5% of 50
= [latex]\frac { 5 }{ 100 }[/latex] x 50 = [latex]\frac { 5 }{ 2 }[/latex] = ₹ 2.50
∴ C.P. = Net Price + Sales
Tax = 50 + 2.50 = ₹ 52.50

(ii) The cost of two soaps at the rate of
₹ 35 each = 2 × 35 = ₹ 70
Sales Tax = 5% of 70
= [latex]\frac { 5 }{ 100 }[/latex] × 70 = [latex]\frac { 7 }{ 2 }[/latex] = ₹ 3.50
∴ C.P. = Net Price + Sales
Tax = 70 + 3.50 = ₹ 73.50

Question 16.
A Super-Bazar prices an item in rupees and paise so that when 4% sales tax is added, no rounding is necessary because the result is exactly in ‘n’ rupees, where ‘n’ is a positive integer. Find the smallest value of ’n’.
Solution:
Let the cost price = x say
∴ If x is increased 4% sales tax is added then
x + 4% of x = n
x + [latex]\frac { 4 }{ 100 }[/latex] × x = n
[latex]\frac { 140x }{ 100 }[/latex] = n
x = x = n × [latex]\frac { 100 }{ 104 }[/latex] = [latex]\frac{25 \times \mathrm{n}}{26}[/latex]
∴ n should be a least multiple of 26, then only the value of the article should be represented in only rupees.

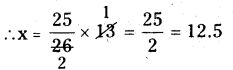
[∵n = 13, 26, 39. from them 13 should betaken]
:. Required value of the article
=12.50 + [latex]\frac { 4 }{ 100 }[/latex] × 12.5
12.50 + 0.5 = ₹13

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 5 Comparing Quantities Using Proportion Ex 5.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson Comparing Quantities Using Proportion Exercise 5.1

Question 1.
Find the ratio of the following
(i) Smita works in office for 6 hours and Kajal works for 8 hours in her office. Find the
ratio of their working hours.
Solution:
The ratio of working hours of smita and kajal = 6:8
= (2 × 3 ) : (2 × 4) = 3 : 4

(ii) One pot contains 8 litre of milk while other contains 750 milliliter.
Solution:
8lit : 750ml
8 × 1000 : 750
= [latex][latex]\frac { 8000 }{ 750 }[/latex][/latex] = 32 : 3

(iii) speed of a cycle is 15km/h and speed of the scooter is 30km/h.
Solution:
The ratio of speeds of a cycle and a sector
= 15 : 30 = (15 × 1) : 15 × 2 = 1 : 2

Question 2.
If the compound ratio of 5:8 and 3:7 is 45:x. Find the value of x.
Solution:
The compound ratio of 5:8 and 3:7
= [latex]\frac{5}{8} \times \frac{3}{7}=\frac{15}{56}[/latex]
According to the sum
15 : 56 = 45 : x
∴ x = 168

Question 3.
If the compound ratio of 7:5 and 8:x is 84:60. Find x.
Solution:
The compound ratio of 7:5 and 8:x
= [latex]\frac{7}{5} \times \frac{8}{x}=\frac{56}{5 x}[/latex]
According to the sum
56 : 5x = 84 : 60

∴ x = 8

Question 4.
The compound ratio of 3:4 and the inverse ratio of 4:5 is 45:x. Find x.
Solution:
The inverse ratio of 4:5 is 45 : x
The compound ratio of 3:4 and 5 : 4
= 45 : x

⇒ x = 16 × 3 = 48
∴ x = 48

Question 5.
In a primary school there shall be 3 teachers to 60 students. If there are 400 students
enrolled in the school, how many teachers should be there in the school in the same ratio?
Solution:
No. of teachers are required for 400 students at the rate of 3 teachers to 60
students are ⇒ 60 : 3 400 : x

∴ x = 20

Question 6.
In the given figure, ABC is a triangle. Write all possible ratios by A
taking measures of sides pair wise.
8cm 10cm
(Hint: Ratio of AB : BC =8 : 6)

Solution:

In ΔABC
AB : BC = 8 : 6 = 4:3
⇒ BC : AB = 6 : 8 = 3: 4
BC : CA = 6 : 10 = 3 : 5
⇒ CA : BC = 10 : 6 = 5 : 3
CA : AB = 10:8=5:4
⇒ AB : CA = 8: 10 = 4: 5

Question 7.
If 9 out of 24 students scored below 75% marks in a test. Find the ratio of student scored below 75% marks to the student scored 75% and above marks.
Solution:
Out of 24 students who got below 75% of marks = 9
Who got 75% and above marks =24 – 9 = 15
∴ The ratio between no. of students
who got less than 75% of marks and
who got 75% and above marks
= 9 : 15 =(3 × 3):(3 × 5) = 3 : 5

Question 8.
Find the ratio of number of vowels in the word’ MISSISSIPPI’ to the number of consonants in the simplest form.
Solution:
No. of vowels in the word MI S S SS! PPI = 4 (IIII)
No. of consonants in that word = 7 (MSSSSPP)
∴ The ratio between vowels and consonants = 4: 7

Question 9.
Rajendra and Rehana own a business. Rehana receives 25% of the profit in each month. If
Rehana received ₹ 2080 in particular month, what is the total profit in that month?
Solution:
Total Profit = x say
25% of x = 2080
⇒ [latex]\frac{25}{100}[/latex] × x = 2080
⇒ [latex]\frac{x}{4}[/latex] = 2080
⇒ x = 2080 × 4
∴ x = ₹ 8320

Question 10.
In triangle ABC, AB = 2.2 cm, BC = 1.5 cm and AC = 2.3 cm. In triangle XYZ, XY = 4.4cm, YZ = 3cm and XZ = 4.6cm. Find the ratio AB:XY, BC:YZ, AC:XZ. Are the lengths of corresponding sides of ΔABC and ΔXYZ are in proportion?
[Hint : Any two triangles are said to be in proportion, if their corresponding sides are in the
same ratio]
Solution:

∴ The corresponding sides of both the triangles are in proportion.
∴ ΔABC ~ ΔXYZ

Question 11.
Madhuri went to a super market. The price changes are as follows. The price of rice reduced by 5% jam and fruits reduced by 8% and oil and dal increased by 10%. Help Madhuri to find the changed prices in the given table.

Item	Original price/kg	Changed price
Rice	₹ 30
Jam	₹ 100
Apples	₹ 280
Oil	₹ 120
Dal	₹ 80

Solution:

Item	Original price/kg	Changed price
Rice	₹ 30	₹28.50
Jam	₹ 100	₹ 92
Apples	₹ 280	₹ 257.6
Oil	₹ 120	₹ 132
Dal	₹ 80	₹ 88

Question 12.
There were 2075 members enrolled in the club during last year. This year enrolment is
decreased by 4%.
(a) Find the decrease in enrolment.
(b) How many members are enrolled during this year?
Solution:
No. of persons are enrolled in the last year = 2075
Present year no. of persons are enrolled
= 4% less than the previous year.
a) Decrease in enrolment = 4% of 2075

b) No.of members are enrolled this
year = 2075 – 4% of 2075
=2075 – 83 = 1992

Question 13.
A farmer obtained a yielding of 1720 bags of cotton last year. This year she expects her crop to be 20% more. How many bags of cotton does she expect this year?
Solution:
During the last year yielding the bags of
cotton = 1720
If she expects 20% crop to be more then
=20% of 1720 .
= [latex]\frac{20}{100}[/latex] × 1720
= 2 × 172
= 344 bags
Her expectation of total bags
= 1720 + 344
= 2064

Question 14.
Points P and Q are both in the line segment AB and on the same side of its midpoint. P divides AB in the ratio 2: 3, and Q divides AB in the ratio 3 :4. If PQ =2, then find the length of the line segment AB.
Solution:
Given that ‘C’ is the midpoint of line segment AB.
Here ‘P’ divides AB inthe ratio 2 : 3
‘Q’ divides AB in the ratio 3: 4

PQ =2 cm [Given]
PQ = QB – PB
= 4 – 3 = 1 part = 2cm
∴ AB = AQ + QB [with respect to Ql
AB = AP+ PB [with respect to P]
L.C.M. of 5, 7 parts = 35 parts
∴ Length of AB 35 parts
= 35 × 2[ ∵ part = 2cm]
= 70cm

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 4 Exponents and Powers Ex 4.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson Exponents and Powers Exercise 4.2

Question 1.
Express the following numbers in the standard form.
(i) 0.000000000947
Solution:
= [latex]\frac{947}{1000000000000}[/latex] = 947 × 10^-12

(ii) 543000000000
Solution:
= 543 × 1000000000 = 543 × 10⁹

(iii) 48300000
Solution:
= 483 × 100000 = 483 × 10⁵

(iv) 0.00009298
Solution:
= [latex]\frac{9298}{100000000}[/latex]
= 9298 × 10^-8

(v) 0.0000529
Solution:
= [latex]\frac{529}{10000000}[/latex]
= 529 × 10^-7

Question 2.
Express the following numbers in the usual form.
(i) 4.37 × 10⁵
Solution:
= 4.37 × 100000
= 437000

(ii) 5.8 × 10⁷
Solution:
= 5.8 × 10000000

(iii) 32.5 × 10^-4
Solution:
= [latex]\frac{32.5}{10^{4}}=\frac{32.5}{10000}[/latex]
= 0.00325

(iv) 3.71529 × 10⁷
Solution:
= 3.71529 × 10000000
= 37152900

(v) 3789 × 10^-5
Solution:
= [latex]\frac{3789}{10^{5}}=\frac{3789}{100000}[/latex]
= 0.03789

(vi) 24.36 × 10^-3
Solution:
= [latex]\frac{24.36}{10^{3}}=\frac{24.36}{1000}[/latex]
= 0.02436

Question 3.
Express the following information in the standard form
(i) Size of the bacteria is 0.0000004 m
Solution:
= [klatex]\frac{4}{10000000}[/latex] m = 4 x 10^-7 m

(ii) The size of red blood cells is 0.000007mm
Solution:
= [latex]\frac{7}{1000000}[/latex] = 7 × 10^-6

(iii) The speed of light is 300000000 m/sec
Solution:
= 3 × 10,00,00,000 = 3 × 10⁸ m/sec

(iv) The distance between the moon and the earth is 384467000 m(app)
Solution:
= 384467 × 1000 m
= 384467 × 10³

(v) The charge of an electron is 0.0000000000000000016 coulombs
Solution:
= 0.0000000000000000016
= [latex]\frac{16}{10000000000000000000}[/latex]
= [latex]\frac{16}{10^{19}}[/latex]
= 16 × 10^-19 coulombs

(vi) Thickness of a piece of paper is 0.0016 cm
Solution:
= 0.0016 cm = [latex]\frac{16}{10000}[/latex]
= [latex]\frac{16}{10^{4}}[/latex]
= 16 × 10^-4 cm

(vii) The diameter of a wire on a computer chip is 0.000005 cm
Solution:
= 0.000005 cm = [latex]\frac{5}{1000000}[/latex] cm
= [latex]\frac{5}{10^{6}}[/latex] cm = 5 × 10^-6 cm

Question 4.
In a stack, there are 5 books, each of thickness 20 mm and 5 paper sheets each of thickness 0.016mm. What is the total thickness of the stack.
Solution:
The thickness of 5 books of a pack
= (5 books × their thickness)
= 5(papers × their thickness)
= (20 mm × 5) + (0.016 mm × 5)
= 100 mm + 0.080 mm
= (100 + 0.080) mm
= 100.08 mm
= 1.0008 × 10² mm

Question 5.
Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
(i) x^-3 × x^-2 = x^-6
Solution:
x^-3 × x^-2 = x^-6
= x^-3+(-2) = x^-6 [∵ a^m × aⁿ = a^{m + n} ]
= x^-5 = x^-6
= -5 = -6(False)
∴ In this case do not agree with Rakesh solution.

(ii) [latex]\frac{X^{3}}{X^{2}}[/latex] = x⁴
Solution:
⇒ x^3-2 = x⁴ [∵ [latex]\frac{a^{m}}{a^{n}}[/latex] = a^{m – n} ]
⇒ x¹ = x⁴
[∵Here bases are equal, so exponents are also equal]
⇒ 1 = 4 (It is false)
∴ I do not agree with Rakesh solution.

(iii) (x²)³ = (x²)³ = x⁸
Solution:
(x²)³ = [latex]x^{2^{3}}[/latex] = x⁸
⇒ (x²)³ = [latex]x^{2^{3}}[/latex]
⇒ x^{2 × 3} = [latex]x^{2^{3}}[/latex]
⇒ x⁶ = x^{2 × 2 × 2}
⇒ x⁶ = x⁸
[∵ Bases are equal, so exponents are also equal]
⇒ 6 = 8
It is false
∴ Rakesh solution is wrong.

(iv) x^-2 = √x
Solution:
⇒ x^-2 = x^1/2
⇒ -2 = 1/2 (it is false)
∴ I don’t agree with Rakesh solution.

(v) 3x^-1 = [latex]\frac{1}{3 x}[/latex]
Solution:
⇒ 3x^-1 = [latex]\frac{1}{3 x}[/latex]
⇒ 3 × 3 = [latex]\frac{x}{x}[/latex]
⇒ x⁰ = 9
⇒ 1 = 9
It is false
∴ I don’t agree with Rakesh solution.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 4 Exponents and Powers Ex 4.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson Exponents and Powers Exercise 4.1

Question 1.
Simplify and give reasons
(i) 4^-3
(ii) (-2) ⁷
(iii) [latex]\left(\frac{3}{4}\right)^{-3}[/latex]
(iv) (-3)^-4
Solution:
(i) 4^-3 [latex]\frac{1}{4^{3}}=\frac{1}{64}[/latex] [∵ a^-n = [latex]\frac{1}{\mathrm{a}^{\prime \prime}}[/latex]

(ii) (-2) ⁷ = -(2) ⁷ = -128
[∵ 7 is an odd number]
[∵ (-a)ⁿ = -(aⁿ) if ‘n’ is odd]

(iii) [latex]\left(\frac{3}{4}\right)^{-3}[/latex] = [latex]\frac{3^{-3}}{4^{-3}}=\frac{4^{3}}{3^{3}}=\left(\frac{4}{3}\right)^{3}[/latex]

(iv) (-3)^-4 = [latex]\frac{1}{(-3)^{4}}[/latex] [∵a^-n = [latex]\frac{1}{a^{n}}[/latex]
= [latex]\frac{1}{(3)^{4}}[/latex] [∵ 4 is even ]
= [latex]\frac{1}{81}[/latex]

Question 2.
Simplify the following:
(i) [latex]\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}[/latex]
(ii) (-2)⁷ x (-2)³ x (-2)⁴
(iii) 4⁴ x [latex]\left(\frac{5}{4}\right)^{4}[/latex]
(iv) [latex]\left(\frac{5^{-4}}{5^{-6}}\right)[/latex] x 5³
(v) (-3) ⁴ x 7⁴
Solution:
(i) [latex]\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}[/latex]
[latex]\left(\frac{1}{2}\right)^{4+5+6}=\left(\frac{1}{2}\right)^{15}=\frac{1}{2^{15}}[/latex]
[∵ a^m x aⁿ = a^{m + n}]

(ii) (-2)⁷ x (-2)³ x (-2)⁴
(-2)^{7 + 3 + 4} = (-2) ¹⁴ = 2 ¹⁴
[∵ (-a)ⁿ = aⁿ is even]

(iii) 4⁴ x [latex]\left(\frac{5}{4}\right)^{4}[/latex]
4⁴ x [latex]\left(\frac{5}{4}\right)^{4}[/latex] = 5⁴
[ ∵ [latex]\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}[/latex] ]

(iv) [latex]\left(\frac{5^{-4}}{5^{-6}}\right)[/latex] x 5³
5^-4 x (5⁶ x 5³) [ ∵ [latex]\frac{1}{a^{-n}}=a^{n}[/latex]
= 5^-4 x 5⁶⁺³ [ ∵ a^m x aⁿ = (a)^m+n
= 5^-4 x 5⁹
= 5^(-4)+9 = 5⁵

(v) (-3) ⁴ x 7⁴
= 3⁴ x 7⁴[.4isevennumber]
=(3 x 7)⁴ [:amxbm=(ab)m]
= (21)⁴

Question 3.
Simplify
(i) [latex]2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}[/latex]
(ii) (4^-1 x 3^-1) ÷ 6^-1
Solution:
(i) [latex]2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}[/latex]
= 2² x 2² x 3² x 3^-1
= 2²⁺² x 3^{2 + ( – 1)}
=2⁴ x 3¹ = 16 x 3 = 48

(ii) (4^-1 x 3^-1) ÷ 6^-1

Question 4.
Simplify and give reasons
(i) (4⁰ + 5^-1) x 5² x [latex]\frac{1}{3}[/latex]
Solution:

(ii) [latex]\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{4}\right)^{-3} \times\left(\frac{1}{5}\right)^{-3}[/latex]
Solution:
= [latex]\left(\frac{1}{2} \times \frac{1}{4} \times \frac{1}{5}\right)^{-3}[/latex]
= [latex]\left(\frac{1}{40}\right)^{-3}[/latex] [∵ a^m x b^m x c^m = (abc)^m
= (40)³ [ ∵][latex]\frac{1}{a^{-n}}[/latex] = aⁿ ]

(iii) (2^-1 + 3^-1 + 4^-1) x [latex]\frac{3}{4}[/latex]
Solution:

(iv) [latex]\frac{3^{-2}}{3}[/latex] x (3⁰ – 3^-1
Solution:

(v) 1 + 2^-1 + 3^-1 + 4⁰
Solution:

(vi) [latex]\left[\left(\frac{3}{2}\right)^{-2}\right]^{2}[/latex]
Solution:

Question 5.
Simplify and give reasons
(i) [latex]\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}[/latex]
Solution:
[latex]\left.\left[(9-4) \div \frac{1}{5}\right)\right]^{2}[/latex]
= [latex]\left[5 \times \frac{5}{1}\right]^{2}[/latex] = (5²)² 5⁴ = 625 [∵ (a^m)ⁿ = a^mn]

(ii) ((5²)³ x 5⁴) ÷ 5⁶
Solution:

Question 6.
Find the value of ’n’ in each of the following:
(i) [latex]\left(\frac{2}{3}\right)^{3} \times\left(\frac{2}{3}\right)^{5}=\left(\frac{2}{3}\right)^{\mathrm{n}-2}[/latex]
Solution:

Here bases are equal, so exponents are
also equal.
⇒ n – 2 = 8
⇒ n = 8 + 2 = 10
∴ n = 10

(ii) (-3)ⁿ⁺¹ x (-3)⁵ = (-3)³
Solution:
⇒(-3)ⁿ⁺¹⁺⁵ = (-3)^-4 [∵ a^m x aⁿ = a^m+n ]
⇒ (-3)ⁿ⁺⁶ = (-3)^-4
⇒ n + 6 = -4
⇒ n = -4 – 6 = -10
⇒ n = -10

(iii) 7²ⁿ⁺¹ ÷ 49 = 7³
Solution:

⇒ 7^2n+1-2 = 7³ [ ∵ [latex]\frac{a^{m}}{a^{n}}=a^{m-n}[/latex] ]
⇒ 7^{2n – 1}= 7³
⇒ 2n – 1 = 3
⇒ 2n = 3 + 1 = 4
⇒ n = [latex]\frac{4}{2}[/latex]
∴ n = 2

Question 7.
Find ’x’ if 2^-3 = [latex]\frac{1}{2^{x}}[/latex]
Solution:
2^-3 = [latex]\frac{1}{2^{x}}[/latex] = 2^-x
⇒ 2^-3 = 2^-x [ [latex]\frac{1}{a^{n}}[/latex] = a^-n ]
⇒ -x = -3
∴ x = 3

Question 8.
Simplify [latex]\left[\left(\frac{3}{4}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\right] \times\left(\frac{3}{5}\right)^{-2}[/latex]
Solution:

Question 9.
If m = 3 and n = 2 find the value of
(i) 9m² – 10n³
(ii) 2m² n²
(iii) 2m³ + 3n² – 5m²n
(iv) mⁿ – n^m
Solution:
1) 9m² – 10n³
= 9(3)² – 10(2)³
= 9 x 9 – 10 x8
= 81 – 80 = 1

(ii) 2m² n²
= 2(3)² (2)²
= 2 x 9 x 4 = 72

(iii) 2m³ + 3n² – 5m²n
= 2(3)³ + 3(2)² – 5(3)²(2)
= (2 x 27) + (3 x 4) – (5 x 9 x 2)
= 54 + 12 – 90
= 66 – 90 = – 24

(iv) mⁿ – n^m
= 3² – 2³
= 3 x 3 – 2 x 2 x 2
= 9 – 8 = 1

Question 10.
Simplify and give reasons [latex]\left(\frac{4}{7}\right)^{-5} \times\left(\frac{7}{4}\right)^{-7}[/latex]
Solution:

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals Ex 3.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals Exercise 3.3

Construct the quadrilateral with the measurements given below :

Question a).
Quadrilateral GOLD: OL = 7.5 cm, GL = 6 cm, LD = 5 cm, DG = 5.5 cm and OD = 10 cm.
(Ex 3.3, Page No. 72)
Solution:
In a quadrilateral GOLD, Rough Diagram
OL = 7.5 cm, GL = 6 cm
LD = 5 cm, DG = 5.5 cm, OD = 10 cm

Construction Steps:

1. Draw a line segment [latex]\overline{OL}[/latex] equal to radius 7.5 cm.
2. With the centres O, L draw arcs with radius 10 cm and 5 cm respectively. These two arcs meet at point ‘D’.
3. With the centres L, D draw arcs equal to 6 cm and 5.5 cm respectively. These two arcs meet at point ‘G’.
4. Join O, G and L, G. Also join O, D and L, D and G, D.
5. ∴ The required quadrilateral GOLD is formed.

Question b).
Quadrilateral PQRS: PQ = 4.2 cm, QR = 3 cm, PS = 2.8 cm, PR = 4.5 cm and QS = 5 cm.
Solution:


In a quadrilateral PQRS
PQ = 4.2 cm PS = 2.8 cm
QR = 3 cm PR = 4.5 cm
QS = 5 cm

Construction Steps:

1. Draw a line segment [latex]\overline{P Q}[/latex] with radius 4.2 cm.
2. With the centres P, Q draw arcs equal to the radius 4.5 cm, 3 cm respectively. These two arcs meet at point R’. Join P, R and Q, R.
3. With the centres Q, P draw arcs equal to the radii 5 cm and 2.8 cm respectively. These two arcs meet at point ‘S’.
4. Join P, S and Q, S and S, R.
5. ∴ The required PQRS quadrilateral is formed.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals Ex 3.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals Exercise 3.2

Construct quadrilateral with the measurements given below:

Question (a).
Quadrilateral ABCD with AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm andAC= 7cm
Solution:
In Quadrilateral ABCD with AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and AC = 7 cm.

Construction Steps:

1. Draw a line segment [latex]\overline{\mathrm{AB}}[/latex] with radius 4.5 cms.
2. With the centres A, B draw arcs equal to 7 cm and 5.5 cm respectively. The intersection of these two arcs keep as ‘C’.
3. Join A, C and B, C.
4. With centres C, A draw arcs equal to 4 cm, 6 cm respectively. These intersecting point is keep as ’D’.
   Join D, C and A, D.
5. ∴ The required quadrilateral ABCD is formed.

Question (b).
Quadrilateral PQRS with PQ = 3.5 cm, QR = 4 cm, RS = 5 cm, PS = 4.5 cm and QS= 6.5 cm
Solution:
In a quadrilateral PQRS,
PQ = 3.5 cm, QR = 4 cm, RS = 5 cm,
PS – 4.5 cm, QS = 6.5 cm

Construction Steps:

1. Draw a line segment [latex]\overline{\mathrm{PQ}}[/latex] with radius 3.5 cm.
2. With the centres P, Q draw arcs equal to 4.5 cm and 6.5 cm respectively.
3. These two arcs meet at point ‘S’.
4. With the centres S, Q draw arcs with radius 5 cm, 4 cm respectively. These two arcs intersected at point ‘R’.
5. Join P, S; Q, S; S, R and Q, R.
6. ∴ The required quadrilateral PQRS is formed.

Question (c).
Parallelogram ABCD with AB = 6cm, CD = 4.5 cm and BD = 7.5 cm
Solution:
In a parallelogram ABCD; AB = 6 cm, BC = 4.5 cm, BD = 7.5 cm
AB = CD (;cm
BC = AD = 4.5 cm
BD = 7.5 cm

Construction Steps:

1. Draw a line segment [latex]\overline{\mathrm{AB}}[/latex] with radius 6 cms.
2. With the centres A, B draw arcs with radius 4.5 cm, 7.5 cm respectively. These two arcs meet at point ‘D’.
3. With the centres D, B draw arcs with radius 6 cm, 4.5 cm respectively. These two arcs meet at point ‘C’.
4. Join A, D and B, C and D, C and B, D.
5. ∴ The required parallelogram ABCD is formed.

Question (d).
Rhombus NICE with NI = 4 cm and IE = 5.6 cm
Solution:
In a rhombus NI = IC = CE = NE = 4 cm, IE = 5.6 cm

Construction Steps:

1. Draw a line segment [latex]\overline{\mathrm{NI}}[/latex] with radius 4 cm.
2. With the centres N, I draw two arcs with radius 4 cm, 5.6 cm respectively. These two arcs meet at point E’.
3. With the centres E, I draw arcs with radius 4 cm. These two arcs meet at point ‘C’.
4. Join N, E and I, E. Also join E, C and I, C.
5. .’. The required rhombus NICE is formed.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.3

Question 1.
Express each of the following decimal in the [latex]\frac{p}{q}[/latex] form.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
Solution:
(i) 0.57 = [latex]\frac{57}{100}[/latex] (∵ two digits are there after the decimal poing)
(ii) 0.176 = [latex]\frac{176}{1000}[/latex]
(iii) 1.00001 = [latex]\frac{100001}{100000}[/latex]
(iv) 25.125 = [latex]\frac{25125}{1000}[/latex]

Question 2.
Express each of the following decimals in the rational form [latex]\frac{p}{q}[/latex]
(1) [latex]0 . \overline{9}[/latex]
(ii) [latex]0 . \overline{57}[/latex]
(iii) [latex]0 .7 \overline{29}[/latex]
(iv) [latex]12.2 \overline{8}[/latex]
Solution:
(i) [latex]0 . \overline{9}[/latex]
Let x = [latex]0 . \overline{9}[/latex]
⇒ x = 0.999 ………………. (1)
Here periodicity is 1. So, equation (1) should be multiplied both sides with
= 10 × x = 10 × 0.999
10 x = 9.999 ………….. (2)

[latex]0 . \overline{9}[/latex] = 1

Second Method:
[latex]0 . \overline{9}=0+\overline{9}=0+\frac{9}{9}[/latex]
= 0 + 1 = 1

(ii) [latex]0 . \overline{57}[/latex]
x = [latex]0 . \overline{57}[/latex] ⇒ x = 0.5757…………(1)
Here periodicity is 2. So, we should multiply with 100
⇒ 100 × x = 100 x 0.5757 …………..
100 × =57.57 ……………………. (2)

(iii) [latex]0 .7 \overline{29}[/latex]
x = [latex]0 .7 \overline{29}[/latex]
x = [latex]0 .7 \overline{29}[/latex] ⇒ x = 0.7979…………(1)
Here periodicity is 2. So, equation (1) should multiply with 100
⇒ 100 × x = 100 × 0.72929 …………..
100 × = 72.929 …………………… (2)

(iv) [latex]12.2 \overline{8}[/latex]
x = (iv) [latex]12.2 \overline{8}[/latex]
⇒ x = 12.288 ………..(1)
Here periodicity is 1. So, equation (1) should multiply with 10
⇒ 100 × x = 100 × 12.288 …………..
10 x = 122.888 …………………… (2)

Question 3.
Find(x + y) ÷ (x – y) if
(i) x = [latex]\frac{5}{2}[/latex], y = [latex]-\frac{3}{4}[/latex]
(ii) x = [latex]\frac{1}{4}[/latex], y = [latex]\frac{3}{2}[/latex]
Solution:
If x = [latex]\frac{5}{2}[/latex], y = [latex]-\frac{3}{4}[/latex] then

ii) x = [latex]\frac{1}{4}[/latex], y = [latex]\frac{3}{2}[/latex]

Question 4.
Divide the sum of [latex]-\frac{13}{5}[/latex] and [latex]\frac{12}{7}[/latex] by the product of [latex]-\frac{13}{7}[/latex] and [latex]-\frac{1}{2}[/latex]
Solution:
Sum of [latex]-\frac{13}{5}[/latex] and [latex]\frac{12}{7}[/latex]

the product of [latex]-\frac{13}{7}[/latex] and [latex]-\frac{1}{2}[/latex]

Question 5.
If [latex]\frac{2}{5}[/latex] of a number exceeds [latex]\frac{1}{7}[/latex] of the same number by 36. Find the number.
Solution:
Let the number be ‘x’ say.
[latex]\frac{2}{5}[/latex] part of x = [latex]\frac{2}{5}[/latex] × x = [latex]\frac{2x}{5}[/latex]
[latex]\frac{1}{7}[/latex] part of x = [latex]\frac{1}{7}[/latex] × x = [latex]\frac{x}{7}[/latex]
∴ According to the sum,

Question 6.
Two pieces of lengths 2[latex]\frac{2}{5}[/latex] m and 3[latex]\frac{3}{10}[/latex] mare cut off from a rope 11 m long. What is the length of the remaining rope?
Soltuion:
The length of the remaining rope

∴ The length of remaining rope
= 5[latex]\frac{1}{10}[/latex] mts.

Question 7.
The cost of 7[latex]\frac{2}{3}[/latex] meters of cloth is ₹12[latex]\frac{3}{4}[/latex] . Find the cost per metre.
Solution:
The cost of 7[latex]\frac{2}{3}[/latex] mts ([latex]\frac{23}{3}[/latex] mts ) of cloth
= ₹ [latex]12 \frac{3}{4}[/latex] = ₹ [latex]\frac{51}{4}[/latex]
∴ The cost of 1m cloth
= [latex]\frac{51}{4} \div \frac{23}{3}=\frac{51}{4} \times \frac{3}{23}=\frac{153}{92}[/latex] = ₹ 1.66

Question 8.
Find the area of a rectangular park which is 18[latex]\frac{3}{5}[/latex]m long and 8[latex]\frac{2}{3}[/latex] in broad.
Solution:
The length of the rectangular park
= 18[latex]\frac{3}{5}[/latex]m = [latex]\frac{93}{5}[/latex]
Its width / breath = 8[latex]\frac{2}{3}[/latex] m = [latex]\frac{26}{3}[/latex] m
∴ Area of the rectangular park
(A) = l × b

Question 9.
What number should [latex]-\frac{33}{16}[/latex] be divided by to get [latex]-\frac{11}{4}[/latex]
Solution:
Let the dividing number be ‘x’ say.

Question 10.
If 36 trousers of equal sizes can be stitched with 64 meters of cloth. What is the length of the cloth required for each trouser?
Solution:
36 trousers of equal sizes can he stitched with 64 mts of cloth, then the length of the cloth ¡s required for each trouser
= 64 ÷ 36
= [latex]\frac{64}{36}=\frac{16}{9}[/latex] = 1 [latex]\frac{7}{9}[/latex]

Question 11.
When the repeating decimal 0.363636 …. is written in simplest fractional form[latex]\frac{p}{q}[/latex] , find the sum p+ q.
Solution:
x = 0.363636………………………….. (1)
Here periodicity is ‘2’. So, equation (1) should be multiplied both sides with 100.
⇒ 100 × x = 100 × 0.363636 …………..
100 x = 36.3636 ………..(2)

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.2

Question 1.
Represent these numbers on the number line.
(i) [latex]\frac{9}{7}[/latex]
(ii) [latex]-\frac{7}{5}[/latex]
Solution:
(i) [latex]\frac{9}{7}[/latex]

(ii) [latex]-\frac{7}{5}[/latex]

Question 2.
Represent [latex]-\frac{2}{13}, \frac{5}{13}, \frac{-9}{13}[/latex] on the number line.
Solution:

Question 3.
Write five rational numbers which are smaller than [latex]\frac{5}{6}[/latex]
Solution:
The rational number which are less than
[latex]\frac{5}{6}=\left\{\frac{4}{6}, \frac{3}{6}, \frac{2}{6}, \frac{1}{6}, \frac{0}{6}, \frac{-1}{6}, \frac{-2}{6} \ldots \ldots .\right\}[/latex]

Question 4.
Find 12 rational numbers between -1 and 2.
Solution:

Question 5.
Find a rational number between [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{4}[/latex]
[Hint : First write the rational numbers with equal denominators.]
Solution:
The given rational numbers are [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{4}[/latex]
[latex]\frac{2}{3} \times \frac{4}{4}=\frac{8}{12}, \frac{3}{4} \times \frac{3}{3}=\frac{9}{12}[/latex]
The rational numbers between [latex]\frac{8}{12}, \frac{9}{12}[/latex] is
[latex]\frac{\left(\frac{8}{12}+\frac{9}{12}\right)}{2}=\frac{\frac{17}{12}}{2}=\frac{17}{24}[/latex]
(∵ the rational number between a, b is [latex]\frac{a+b}{2}[/latex] )
∴ the rational number between [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{4}[/latex] is [latex]\frac{17}{24}[/latex]

Question 6.
Find ten rational numbers between [latex]-\frac{3}{4}[/latex] and [latex]\frac{5}{6}[/latex]
Solution:

The 10 rational numbers between [latex]-\frac{9}{12}[/latex] and [latex]\frac{10}{12}[/latex] are

∴ We can select any 10 rational numbers from the above number line.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.1

Question 1.
Name the properly Involved in the following examples.

vii) 7a + (-7) = 0
viii) x + [latex]\frac{1}{x}[/latex] = 1(x ≠ 0)
ix) (2 x x) + (2 x 6) = 2 x (x + 6)
Solution:
i) Additive identity
ii) Distributive law
iii) Multiplicative identity
iv) Multiplicative identity
v) Commutative law of addition
vi) Closure law in multiplication
vii) Additive inverse
viii) Multiplicative inverse
ix) Distributive

Question 2.
Write the additive and the multiplicative inverses of the following.
i) [latex]\frac{-3}{5}[/latex]
ii) 1
iii) 0
iv) [latex]\frac{7}{9}[/latex]
v) -1
Solution:

Question 3.
Fill in the blanks



Solution:
i) [latex]\left(\frac{-12}{5}\right)[/latex]
ii) [latex]\left(\frac{4}{3}\right)[/latex]
iii) [latex]\left(\frac{9}{11}\right)[/latex]
iv) [latex]\left(\frac{6}{7}\right)[/latex]
v) [latex]\left(\frac{3}{4}, \frac{1}{3}\right)[/latex]
vi) 0

Question 4.
Multiply [latex]\frac{2}{11}[/latex] by the reciprocal of [latex]\frac{-5}{14}[/latex]
Solution:
The reciprocal of [latex]\frac{-5}{14}[/latex] is [latex]\frac{-14}{5}[/latex]
( ∵ [latex]\left(\frac{-5}{14}\right) \times\left(\frac{-14}{5}\right)=1[/latex] )
∴ The product of [latex]\frac{2}{11}[/latex] and [latex]\frac{-14}{5}[/latex] is
[latex]\frac{2}{11} \times\left(\frac{-14}{5}\right)=\frac{-28}{55}[/latex]

Question 5.
Which properties can be used computing [latex]\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex]
Solution:
The following properties are involved in the product of
[latex]\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex]
i) Multiplicative associative property.
ii) Multiplicative inverse.
iii) Multiplicative identity.
iv) Closure with addition

Question 6.
Verify the following
[latex]\left(\frac{5}{4}+\frac{-1}{2}\right)+\frac{-3}{2}=\frac{5}{4}+\left(\frac{-1}{2}+\frac{-3}{2}\right)[/latex]
Solution:

Question 7.
Evaluate [latex]\frac{3}{5}+\frac{7}{3}+\left(\frac{-2}{5}\right)+\left(\frac{-2}{3}\right)[/latex] after rearrangement.
Solution:

Let x = [latex]1.2 \overline{4}[/latex]
⇒ x = 1.244……. …………………(1)
Here periodicity of equation (1) is 1. So
it should be multiplied by 10 on both
sides.
⇒ 10 x x = 10 x 1.244
10x = 12.44 …………..(2)

Question 8.
Subtract
(i) [latex]\frac{3}{4}[/latex] from [latex]\frac{1}{3}[/latex]
(ii) [latex]\frac{-32}{13}[/latex] from 2
(iii) -7 from [latex]\frac{-4}{7}[/latex]
Solution:

Question 9.
What numbers should be added to [latex]\frac{-5}{8}[/latex] so as to get [latex]\frac{-3}{2}[/latex] ?
Solution:
Let the number to be add ‘x’ say

∴ [latex]\frac{-7}{8}[/latex] should be added to [latex]\frac{-5}{8}[/latex] then we will get [latex]\frac{-3}{2}[/latex]

Question 10.
The sum of two rational numbers is 8 If one of the numbers is [latex]\frac{-5}{6}[/latex] find the other.
Let the second number be ‘x’ say
⇒ [latex]x+\left(\frac{-5}{6}\right)=8[/latex]
⇒[latex]8+\frac{5}{6}=\frac{48+5}{6}=\frac{53}{6}[/latex]
∴ The other number (x) = [latex]\frac{53}{6}[/latex]

Question 11.
Is subtraction associative in rational numbers? Explain with an example.
Solution:
Let [latex]\frac{1}{2}, \frac{3}{4}, \frac{-5}{4}[/latex] are any 3 rational numbers.
Associative property under subtraction
a – (b – c) = (a – b) – c

∴ L.H.S. ≠ R.H.S.
∴ a – (b – c) ≠ (a – b) – c
∴ Subtraction is not an associative in rational numbers.

Question 12.
Verify that – (-x) = x for
(i) x = [latex]\frac{2}{15}[/latex]
(ii) x = [latex]\frac{-13}{15}[/latex]
Solution:

Question 13.
Write-
(i) The set of numbers which do not have any additive identity
(ii) The rational number that does not have any reciprocal
(iii) The reciprocal of a negative rational number.
Solution:
i) Set of natural numbers ’N’ doesn’t possesses the number ‘0’.
ii) The rational number ‘0’ has no multiplicative inverse.
[ ∵ 1/0 is not defined]
iii) The reciprocal of a negative rational number is a negative rational number.
Ex : Reciprocal of [latex]\frac{-2}{5}=\frac{-5}{2}[/latex]