AP State Syllabus AP Board 8th Class Maths Solutions Chapter 4 Exponents and Powers Ex 4.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 4th Lesson Exponents and Powers Exercise 4.1
![]()
Question 1.
Simplify and give reasons
(i) 4-3
(ii) (-2) 7
(iii) \(\left(\frac{3}{4}\right)^{-3}\)
(iv) (-3)-4
Solution:
(i) 4-3 \(\frac{1}{4^{3}}=\frac{1}{64}\) [∵ a-n = \(\frac{1}{\mathrm{a}^{\prime \prime}}\)
(ii) (-2) 7 = -(2) 7 = -128
[∵ 7 is an odd number]
[∵ (-a)n = -(an) if ‘n’ is odd]
(iii) \(\left(\frac{3}{4}\right)^{-3}\) = \(\frac{3^{-3}}{4^{-3}}=\frac{4^{3}}{3^{3}}=\left(\frac{4}{3}\right)^{3}\)
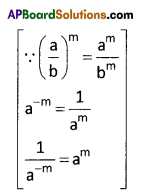
(iv) (-3)-4 = \(\frac{1}{(-3)^{4}}\) [∵a-n = \(\frac{1}{a^{n}}\)
= \(\frac{1}{(3)^{4}}\) [∵ 4 is even ]
= \(\frac{1}{81}\)
![]()
Question 2.
Simplify the following:
(i) \(\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}\)
(ii) (-2)7 x (-2)3 x (-2)4
(iii) 44 x \(\left(\frac{5}{4}\right)^{4}\)
(iv) \(\left(\frac{5^{-4}}{5^{-6}}\right)\) x 53
(v) (-3) 4 x 74
Solution:
(i) \(\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}\)
\(\left(\frac{1}{2}\right)^{4+5+6}=\left(\frac{1}{2}\right)^{15}=\frac{1}{2^{15}}\)
[∵ am x an = am + n]
(ii) (-2)7 x (-2)3 x (-2)4
(-2)7 + 3 + 4 = (-2) 14 = 2 14
[∵ (-a)n = an is even]
(iii) 44 x \(\left(\frac{5}{4}\right)^{4}\)
44 x \(\left(\frac{5}{4}\right)^{4}\) = 54
[ ∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\) ]
(iv) \(\left(\frac{5^{-4}}{5^{-6}}\right)\) x 53
5-4 x (56 x 53) [ ∵ \(\frac{1}{a^{-n}}=a^{n}\)
= 5-4 x 56+3 [ ∵ am x an = (a)m+n
= 5-4 x 59
= 5(-4)+9 = 55
(v) (-3) 4 x 74
= 34 x 74[.4isevennumber]
=(3 x 7)4 [:amxbm=(ab)m]
= (21)4
![]()
Question 3.
Simplify
(i) \(2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}\)
(ii) (4-1 x 3-1) ÷ 6-1
Solution:
(i) \(2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}\)
= 22 x 22 x 32 x 3-1
= 22+2 x 32 + ( – 1)
=24 x 31 = 16 x 3 = 48
(ii) (4-1 x 3-1) ÷ 6-1

Question 4.
Simplify and give reasons
(i) (40 + 5-1) x 52 x \(\frac{1}{3}\)
Solution:
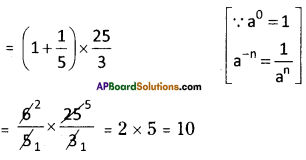
(ii) \(\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{4}\right)^{-3} \times\left(\frac{1}{5}\right)^{-3}\)
Solution:
= \(\left(\frac{1}{2} \times \frac{1}{4} \times \frac{1}{5}\right)^{-3}\)
= \(\left(\frac{1}{40}\right)^{-3}\) [∵ am x bm x cm = (abc)m
= (40)3 [ ∵]\(\frac{1}{a^{-n}}\) = an ]
![]()
(iii) (2-1 + 3-1 + 4-1) x \(\frac{3}{4}\)
Solution:
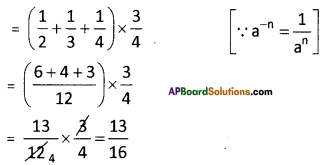
(iv) \(\frac{3^{-2}}{3}\) x (30 – 3-1
Solution:

![]()
(v) 1 + 2-1 + 3-1 + 40
Solution:

(vi) \(\left[\left(\frac{3}{2}\right)^{-2}\right]^{2}\)
Solution:

![]()
Question 5.
Simplify and give reasons
(i) \(\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}\)
Solution:
\(\left.\left[(9-4) \div \frac{1}{5}\right)\right]^{2}\)
= \(\left[5 \times \frac{5}{1}\right]^{2}\) = (52)2 54 = 625 [∵ (am)n = amn]
(ii) ((52)3 x 54) ÷ 56
Solution:
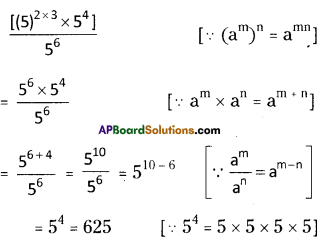
Question 6.
Find the value of ’n’ in each of the following:
(i) \(\left(\frac{2}{3}\right)^{3} \times\left(\frac{2}{3}\right)^{5}=\left(\frac{2}{3}\right)^{\mathrm{n}-2}\)
Solution:
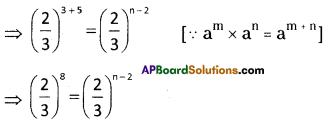
Here bases are equal, so exponents are
also equal.
⇒ n – 2 = 8
⇒ n = 8 + 2 = 10
∴ n = 10
![]()
(ii) (-3)n+1 x (-3)5 = (-3)3
Solution:
⇒(-3)n+1+5 = (-3)-4 [∵ am x an = am+n ]
⇒ (-3)n+6 = (-3)-4
⇒ n + 6 = -4
⇒ n = -4 – 6 = -10
⇒ n = -10
(iii) 72n+1 ÷ 49 = 73
Solution:
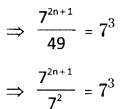
⇒ 72n+1-2 = 73 [ ∵ \(\frac{a^{m}}{a^{n}}=a^{m-n}\) ]
⇒ 72n – 1= 73
⇒ 2n – 1 = 3
⇒ 2n = 3 + 1 = 4
⇒ n = \(\frac{4}{2}\)
∴ n = 2
Question 7.
Find ’x’ if 2-3 = \(\frac{1}{2^{x}}\)
Solution:
2-3 = \(\frac{1}{2^{x}}\) = 2-x
⇒ 2-3 = 2-x [ \(\frac{1}{a^{n}}\) = a-n ]
⇒ -x = -3
∴ x = 3
![]()
Question 8.
Simplify \(\left[\left(\frac{3}{4}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\right] \times\left(\frac{3}{5}\right)^{-2}\)
Solution:

Question 9.
If m = 3 and n = 2 find the value of
(i) 9m2 – 10n3
(ii) 2m2 n2
(iii) 2m3 + 3n2 – 5m2n
(iv) mn – nm
Solution:
1) 9m2 – 10n3
= 9(3)2 – 10(2)3
= 9 x 9 – 10 x8
= 81 – 80 = 1
(ii) 2m2 n2
= 2(3)2 (2)2
= 2 x 9 x 4 = 72
(iii) 2m3 + 3n2 – 5m2n
= 2(3)3 + 3(2)2 – 5(3)2(2)
= (2 x 27) + (3 x 4) – (5 x 9 x 2)
= 54 + 12 – 90
= 66 – 90 = – 24
(iv) mn – nm
= 32 – 23
= 3 x 3 – 2 x 2 x 2
= 9 – 8 = 1
![]()
Question 10.
Simplify and give reasons \(\left(\frac{4}{7}\right)^{-5} \times\left(\frac{7}{4}\right)^{-7}\)
Solution:
