Category: Class 10

Students can go through AP SSC 10th Class Maths Notes Chapter 6 Progressions to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 6 Progressions

→ The array of numbers following some rule is called a number pattern.
E.g.: 4, 6, 4, 6, 4, 6,…….

→ There is a relationship between the numbers of a pattern.

→ Each number in a pattern is called a term.

→ The series or list of numbers formed by adding or subtracting a fixed number to / from the preceding terms is called an Arithmetic Progression, simply A.P.
E.g.: 3, 5, 7,9, 11, ……

→ In the above list, each term is obtained by adding ‘2’ to the preceding term except the first term.

→ Also, we find that the difference between any two successive terms is the same throughout the series. This is called “common difference”.

→ The general form of an A.P. is
a, a + d, a + 2d, a + 3d,………, a + (n – 1) d.
Where‘a’is the first term, d is common difference.
Here d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = …….. = a_n – a_n-1

→ If the number of terms of an A.P. is finite, then it is a finite A.P.
E.g.: 10, 8, 6, 4, 2.

→ If the number of terms of an A.P. is infinite, then it is an infinite A.P.
E.g.: 4, 8, 12, 16, …….

→ If d > 0, then a_n > a_n-1 and if d < 0, then a_n < a_n-1

→ The general term or nth term of an A.P is a_n = a + (n – 1) d.
E.g.: The 10th term of 10, 6, 2, -2, ……. is
Here a = 10 ; d = a₂ – a₁ = 6 – 10 = -4
∴ a₁₀ = a + (n – 1) d = 10 + (10 – 1) × -4 = 10 – 40 + 4 = -26

→ Sum of first n-terms of an A.P. is S_n = [latex]\frac{n}{2}[/latex][a + l] where a is the first term and l is the last term.
E.g.: 1 + 2 + 3 + …… + 80 = [latex]\frac{80}{2}[/latex](1 + 80) = 40 × 81 = 3240.

→ Sum of the first n-terms of an A.P. is given by, S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
Also, a_n = S_n – S_n-1.

→ In a series of numbers, if every number is obtained by multiplying the preceding number by a fixed number except for the first term, such arrangement is called geometric progression or G.P.
E.g.: 4, 8, 16, 32, 64,……
Here, starting from the second term, each term is obtained by multiplying the preceding term by 2.
The first term may be denoted by ‘a’, then we also see that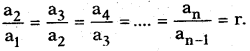
We call it “common ratio”, denoted by ‘r’

→ The general form of a G.P. is
a, ar, ar², ar³, ……. ar^n-1
i.e., a₁ = a, a₂ = ar, a₃ = ar², a_n = ar^n-1.

Students can go through AP SSC 10th Class Maths Notes Chapter 5 Quadratic Equations to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 5 Quadratic Equations

→ The general form of a linear equation in one variable is ax + b = c.

→ Any equation of the form p(x) = 0 where p(x) is a polynomial of degree 2, is a quadratic equation.

→ If p(x) = 0 whose degree is 2 is written in descending order of their degrees, then we say that the quadratic equation is written in the standard form.

→ The standard form of a quadratic equation is ax² + bx + c = 0 where a ≠ 0. We can write it as y = ax² + bx + c.

→ There are various occasions in which we make use of Q.E. in our day-to-day life.
Eg : The height of a rocket is defined by a Q.E.

→ Let ax² + bx + c = 0 be a quadratic equation. A real number α is called a root of the Q.E. if aα² + bα + c = 0. And x = α is called a solution of the Q.E.
(i.e.) the real value of x for which the Q.E ax² + bx + c = 0 is satisfied is called its solution.

→ Zeroes of the Q.E. ax² + bx + c = 0 and the roots of the Q.E. ax² + bx + c = 0 are the same.

→ To factorise a Q.E. ax² + bx + c = 0, we find p, q ∈ R such that p + q = b and pq = ac. This process is called Factorising a Q.E. by splitting its middle term.
Eg : 12x² + 13x + 3 = 0
here a = 12; b = 13; c = 3
a.c = 12 × 3 = 36 = 4 × 9 and
b = 4 + 9 here p = 9 and q = 4
Now 12x² + 13x + 3 = 0
⇒ 12x² + 9x + 4x + 3 = 0
⇒ 3x(4x + 3) + 1 (4x + 3) = 0
⇒ (4x + 3) (3x + 1) = 0
Here 4x + 3 = 0 or 3x + 1 = 0
⇒ 4x = -3 or 3x = -1
⇒ x = [latex]\frac{-3}{4}[/latex] or [latex]\frac{-1}{3}[/latex]
[latex]\frac{-3}{4}[/latex] and [latex]\frac{-1}{3}[/latex] are called the roots of the Q.E. 12x² + 13x + 3 = 0 and x = [latex]\frac{-3}{4}[/latex] or [latex]\frac{-1}{3}[/latex] is the solution of the Q.E. 12x² + 13x + 3 = 0.

→ In the above example, (4x + 3) and (3x +1) are called the linear factors of the Q.E. 12x² + 13x + 3 = 0.

→ We can factorise a Q.E. by adjusting its left side so that it becomes a perfect square.
Eg: x² + 6x + 8 = 0
⇒ x² + 2.x.3 + 8 = 0
⇒ x² + 2.x.3 = -8
The L.H.S. is of the form a² + 2ab
∴ By adding b² it becomes a perfect square
∴ x² + 2.x.3 + 3² = -8 + 3²
⇒ (x + 3)² = -8 + 9
⇒ (x + 3)² = 1
⇒ x + 3 = ± 1 Now we take x + 3 = 1 or x + 3 = -l
⇒ x = -2 or x = -4

→ Adjusting a Q.E. of the form ax² + bx + c = 0 so that it becomes a perfect square.
Step – 1 : ax² + bx + c = 0 ⇒ ax² + bx = -c ⇒ x² + [latex]\frac{b}{a}[/latex]x = [latex]\frac{-c}{a}[/latex]
Step – 2 :

Step – 3 :

Step – 4 : Solve the above.
E.g: 5x² – 6x + 2 = 0

→ Let ax² + bx + c = 0 (a ≠ 0) be a Q.E., then b² – 4ac is called the Discriminant of the Q.E.

→ If b² – 4ac > 0, then the roots of the Q.E. ax² + bx + c = 0 are given by
x = [latex]\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}[/latex]. This is called quadratic formula to find the roots.

The nature of the roots of a Q.E. can be determined either by its discriminant or its graph.
Q.E.: y = ax² + bx + c.

Students can go through AP SSC 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables

→ An equation of the form ax + by + c = 0 where a, b, c are real numbers and where at least one of a or b is not zero (i.e, a² + b² ≠ 0) is called a linear equation in two variables x and y.

→ A pair of equations in the same two variables forms a pair of linear equations. The system of pair of equations in general a₁x + b₁y + c₁ = 0 ; a₂x + b₂y+ c₂ = 0
where a₁, a₂, b₁, b₂, c₁, c₂ ∈ R such that a₁² + b₁² ≠ 0 and a₂² + b₂² ≠ 0

→ A pair of linear equations in two variables can be represented and solved by
a) Graphical method
b) Model method
c) Algebraic methods
i) Substitution method
ii) Elimination method
iii) Cross-multiplication method.

→ Graphical method: The two linear equations in two variables are represented by two straight lines on a graph sheet.
a) If they intersect at a point, then the point gives the unique solution of the two equations. In this case the two equations are consistent.
b) If the lines coincide, then there are infinitely many solutions. Each point on the line represents a solution. In this case, we say that the pair of equations is dependent or consistent.
c) If the two lines are parallel to one another, then the pair of equations has no solution. In this case we say that the pair of equations is inconsistent. Substitution method : In this method, we make one of the variables x or y as the subject from the first equatiori. We substitute this value in the second equation and get the value of the variable involved, then by substituting this value in any of the equations we get the value of second variable.
Eg : 2x + 4y = 16 …….. (1)
3x – 8y = – 18 …….. (2)
From equation (1); 2x + 4y = 16 ⇒ 2x = 16 – 4y ⇒ x = [latex]\frac{16-4y}{2}[/latex]
Substituting x = [latex]\frac{16-4y}{2}[/latex] in the second equation
[latex]3\left(\frac{16-4 y}{2}\right)[/latex] – 8y = -18
48 – 12y – 16y = – 18 × 2
-28y = -36 – 48
y = [latex]\frac{-84}{-28}[/latex] = 3
Substituting y = 3 in (1), 2x + 4y = 16
2x + 4(3) = 16
2x = 16 – 12
x = 2

→ Elimination method: In this method we first try to eliminate one of the two variables and by reducing the system to equation in one variable. We then solve for the variable.
The following steps may be adopted:
Step – 1: Multiply both the equations by some suitable non-zero constants to make the co-efficients of one variable (either x or y) numerically equal.
Step – 2: Add or subtract one equation from other so that one variable gets eliminated. If we get an equation in one variable, proceed to step 3.
If in step – 2, we obtain a true statement involving no variable, then the original pair of equations has infinitely many solutions.
If in step – 2, we obtain a false statement involving no variable, then the original pair of equations has no solutions, i.e., it is inconsistent.
Step – 3: Solve the equation in one variable (x or y) so obtained to get its value.

→ Cross-multiplication method: Let the pair of equations be a₁x + b₁y + c₁ = 0 ; a₂x + b₂y+ c₂ = 0

→ In every case, the obtained solutions should always be verified with the original equations.
Let a₁x + b₁y + c₁ = 0 and a₂x + b₂y+ c₂ = 0, form a pair of linear equations. Then the following situations can arise,
Case – (i): [latex]\frac{a_{1}}{a_{2}}[/latex] ≠ [latex]\frac{b_{1}}{b_{2}}[/latex] – pair of linear equations is consistent.
Case – (ii): [latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{b_{1}}{b_{2}}[/latex] ≠ [latex]\frac{c_{1}}{c_{2}}[/latex] – pair of linear equations is inconsistent.
Case – (iii): [latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{b_{1}}{b_{2}}[/latex] = [latex]\frac{c_{1}}{c_{2}}[/latex] – pair of linear equations is dependent and consistent.

→ There are several situations which can be mathematically represented by two equa¬tions that are not linear to start with. But we alter them so that they are reduced to a pair of linear equations.

→ The pair of values of the variables x and y for which the pair of equations is satisfied is called the solution pair.

Students can go through AP SSC 10th Class Maths Notes Chapter 3 Polynomials to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 3 Polynomials

→ Polynomial: An algebraic expression in which the variables involved have only non-negative integer power is called a polynomial.
Ex: 2x + 5, 3x² + 5x + 6, -5y, x³, etc.

→ Polynomials are constructed using constants and variables.

→ Coefficients operate on variables, which can be raised to various powers of non negative integer exponents.
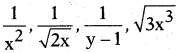, etc. are not polynomials.

→ General form of a polynomial having n^th degree is p(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 …….. + a_n-1x + a_n where a₀, a₁, a₂,…… a_n-1, a_n are real coefficients and a₀ ≠ 0.

→ Degree of a polynomial:
The exponent of the highest degree term in a polynomial is known as its degree.
In other words, the highest power of x in a polynomial f(x) is called the degree of a polynomial f(x).
Example:
i) f(x) = 5x + [latex]\frac{1}{3}[/latex] is a polynomial in the variable x of degree 1.
ii) g(y) = 3y² – [latex]\frac{5}{2}[/latex]y + 7 is a polynomial in the variable y of degree 2.

→ Zero polynomial: A polynomial of degree zero is called zero polynomial that are having only constants.
Ex: f(x) = 8, f(x) = -[latex]\frac{5}{2}[/latex]

→ Linear polynomial: A polynomial of degree one is called linear polynomial.
Ex: f(x) = 3x + 5, g(y) = 7y – 1, p(z) = 5z – 3.
More generally, any linear polynomial in variable x with real coefficients is of the form f(x) = ax + b, where a and b are real numbers and a ≠ 0.
Note: A linear polynomial may be a monomial or a binomial because linear polynomial f(x) = [latex]\frac{7}{5}[/latex]x – [latex]\frac{5}{2}[/latex] is a binomial, whereas the linear polynomial g(x) = [latex]\frac{2}{5}[/latex] x is a monomial.

→ Quadratic polynomial: A polynomial of degree two is called quadratic polynomial.
Ex: f(x) = 5x², f(x) = 7x² – 5x, f(x) = 8x² + 6x + 5.
More generally, any quadratic polynomial in variable x with real coefficients is of the form f(x) = ax² + bx + c, where a, b and c are real numbers and a ≠ 0.
Note: A quadratic polynomial may be a monomial or a binomial or a trinomial.
Ex: f(x) = [latex]\frac{1}{5}[/latex]x² is a monomial, g(x) = 3x² – 5 is a binomial and
h(x) = 3x² – 2x + 5 is a trinomial.

→ Cubic polynomial: A polynomial of degree three is called cubic polynomial.
Ex: f(x) = 8x³, f(x) = 9x³ + 5x²
f(y) = 11y³ – 9y² + 7y,
f(z) = 13z³ – 12z² + 11z + 5.

→ Polynomial of degree ‘n’ in standard form: A polynomial in one variable x of degree n is an expression of the form f(x) = a_nxⁿ + a_n-1x^n-1 + …….. + a₁x + a₀ where a₀, a₁, a₂,…… a_n, a_n are constants and a_n ≠ 0.
In particular, if a₀ = a₁ = a₂ = …… = a_n = 0 (all the constants are zero; we get the constants zero), we get the zero polynomial which is not defined.

→ Value of a polynomial at a given point: If p(x) is a polynomial in x and α is a real number. Then the value obtained by putting x = a in p(x) is called the value of p(x) at x = α.
Ex : Let p(x) = 5x² – 4x + 2, then its value at x = 2 is given by
p(2) = 5(2)² – 4(2) + 2 = 5(4) – 8 + 2 = 20 – 8 + 2 = 14 Thus, the value of p(x) at x = 2 is 14.

→ Graph of a polynomial: In algebraic or in set theory language, the graph of a polynomial f(x) is the collection (or set) of all points (x, y) where y = f(x).
i) Graph of a linear polynomial ax + b is a straight line.
ii) The graph of a quadratic polynomial (ax² + bx + c) is U – shaped, called parabola.

→ If a > 0 in ax² + bx + c, the shape of parabola is opening upwards ‘∪’.

→ If a < 0 in ax² + bx + c, the shape of parabola is opening downwards ‘∩’

→ Relationship between the zeroes and the coefficient of a polynomial:

Note: Formation of a cubic polynomial : Let α, β, and γ be the zeroes of the polynomial.
∴ Required cubic polynomial = (x – α) (x – β) (x – γ).

→ How to make a quadratic polynomial with the given zeroes : Let the zeroes of a quadratic polynomial be α and β.
∴ x = α, x = β
Then, obviously the quadratic polynomial is (x – α) (x – β) i.e., x² – (α + β)x 4- ap.
i.e., x² – (sum of the zeroes) x + product of the zeroes.

→ Division Algorithm : If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that, p(x) = g(x) × q(x) + r(x)
i.e., Dividend = Divisor × Quotient + Remainder
where, r(x) = 0 or degree of r(x) < degree of g(x). This result is known as the division algorithm for polynomials.

→ Some useful relations:
α² + β² = (α + β)² – 2αp
(α – β)² = (α + β)² – 4αβ
α² – β² = (α + β) (α – β) = (α + β)[latex]\sqrt{(\alpha+\beta)^{2}-4 \alpha \beta}[/latex]
α³ + β³ = (α + β)³ – 3αβ(α + β)
α³ – β³ = (α – β)³ + 3αβ(α – β)

Students can go through AP SSC 10th Class Maths Notes Chapter 2 Sets to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 2 Sets

→ Set theory is comparatively a new concept in mathematics.

→ This theory was developed by George Cantor.

→ A well defined collection of objects or ideas is known as “set”.

→ Well defined means that:
i) All the objects in the set should have a common feature or property.
ii) It should be possible to decide whether any given object belongs to the set or not.
Example or comparision of well defined and not well defined collections:

Not well defined collections	Well defined collections
i) A family of rich persons	i) A family of persons having more than one crore rupees
ii) A group of tall students	ii) A group of students, with height 160 cm or more
iii) A group of numbers	iii) A group of even natural numbers less than 15

→ Some more examples of well defined collections:
i) Vowels of English alphabets, namely a, e, i, o, u.
ii) Odd natural numbers less than 11, namely 1, 3, 5, 7, 9.
iii) The roots of the equation x² – 3x + 2 = 0, i.e., 1 and 2.

→ Objects, elements and members of a set are synonymous words.

→ Sets are usually denoted by the capital letters like A, B, C, X, Y, Z, etc.

→ An object belonging to a set is known as a member/element/individual of the set.

→ The elements of a set are represented by small case letters,
i.e., a, b, c, , x, y, z, etc.

→ If ‘b’ is an element of a set A, then we say that ‘b’ belongs to A.

→ The word ‘belongs to’ is denoted by the Greek symbol ‘∈’.

→ Thus, in a notation form, ‘b’ belongs to A is written as b ∈ A and ‘c’ does not belong to ‘A’ is written as c ∉ A.

→ Representation of sets: Sets are generally represented by the following two methods.
i) Roster (or) Tabular form
ii) Rule method (or) Set builder form.

→ Roster (or) Tabular form: In this form, all elements of the set are written, separated by commas, within curly brackets.
Example:
i) The set of all natural numbers less than 5 is represented as N = {l,2,3,4}
ii) The set of all letters in the word “JANUARY” is represented as B = {A, J, N, R, U, Y}
Note:
a) In a set notation, order is not important.
b) The elements of a set are generally not repeated in a particular set.

→ Set builder form (or) Rule method: In this method, a set is described by using a representative and stating the property (or) properties which the elements of the set satisfy, through the representative.
Example:
i) Set of all natural numbers less than 5.
A = {x : x ∈ N, x < 5}
ii) Set of vowels of the English alphabet.
V = {x : x is a vowel in the English alphabet)
Note: It may be observed that we describe the set by using a symbol (x or y or z etc.) for elements of the set.

→ Types of set:

→ Empty set (or) Null set (or) Void set: A set, which does not contain any element is called an empty set (or) a null set (or) a void set.

→ Empty set is denoted by ∅ (or) { }

Example :
A = (x : x is a natural number smaller than 1}
B = {x : x² – 2 = 0 and x is a rational number}
C = (x : x is a man living on the moon}
Note: ∅ and { 0 } are two different sets. {0} is a set containing the single element ‘0’ while { } is a null set.

→ Singleton set: A set consisting of a single element is called a singleton set.
Examples:
{ 0 }, {- 7} are singleton sets.

→ Finite set: A set which is possible to count the number of elements of that set is called finite set.
Example – 1 : The set {3, 4, 5, 6} is a finite set, because it contains a definite number of elements i.e., only 4 elements.
Example – 2 : The set of days in a week is a finite set.

Example – 3 : An empty set, which does not contain any element (no element) is also a finite set.

→ Infinite set: A set whose elements cannot be listed, that type of set is called infinite set.

Example : i) B = {x : x is an even number}
ii) J = {x : x is a multiple of 7}
iii) The set of all points in a plane. s|s A set is infinite if it is not finite.

→ Equal sets: Two sets are said to be equal, if they have exactly the same elements.
For example: The set A and B are having same elements i.e., watch, ring, flower are said to be equal sets.

→ Cardinal number: The number of elements in a set is called the cardinal number of the set.
Example: Consider the finite set A = {1, 2, 4}
Number of elements in set ‘A’ is 3.
It is represented by n(A) = 3

→ Universal set: A set which consists of all the sets under consideration (or) discussion is called the universal set. (or) A set containing all objects or elements and of which all other sets or subsets.
It is usually denoted by ∪ (or) μ.

The universal set is usually represented by rectangles.
Example:
i) The set of real numbers is universal set for number theory.
Here ‘R’ is a universal set.
ii) If we want to study various groups of people of our state, universal set is the set of all people in Andhra Pradesh.

→ Subset: If every element of first set (A) is also an element of second set (B), then first set (A) is said to be a subset of second set (B).

→ It is represented as A ⊂ B.
Example :
Set A = {2, 4, 6, 8} is a subset of .
Set B = {1,2, 3, 4,5, 6, 7, 8}

→ Empty set is a subset of every set.

→ Every set is a subset of itself.

→ Consider ‘A’ and ‘B’ are two sets, if A ⊂ B and B ⊂ A ⇔ A = B.

→ A set doesn’t change if one or more elements of the set are repeated.

→ If A ⊂ B, B ⊂ C ⇒ A ⊂ C.

→ Venn Diagrams: Venn-Euler diagram or simply Venn diagram is a way of representing the relationships between sets.

→ These diagrams consist of rectangles and closed curves usually circles.
Example: Consider that U = {1, 2, 3, ……, 10} is
the universal set of which, A = {2, 4, 6, 8, 10} is a subset.
Then the Venn diagram is as:

→ Basic operations on sets: In sets, we define the operations of union, intersection and difference of sets.

→ Union of sets: The union of two or more sets is the set of all those elements which are either individual (or) both in common.

→ In symbolic form, union of two sets A and B is written as A ∪ B and usually read as “A union B”.

→ Set builder form of A ∪ B is A ∪ B = (x : x ∈ A or x ∈ B}

→ The union of the sets can be represented by a Venn diagram as shown (shaded portion).

→ It is evident from the definition that A ⊆ A ∪ B; B ⊆ A ∪ B.

→ Roster form of union of sets : Let A = {a, e, i, o, u} and B = (a, i, u} then A ∪ B = {a, e, i, o, u} ∪ { a, i, u} = {a, e, i, o, u}

→ Intersection of sets: The intersection of two sets A and B is the set of all those elements which belong to both A and B.

→ We denote intersection by A ∩ B.

→ We read A ∩ B as “A intersection B”.

→ Symbolically, we write A ∩ B = (x : x ∈ A and x ∈ B}

→ The intersection of A and B can be illustrated in the Venn diagram as shown in the shaded portion in the adjacent figure.

→ The intersection of A and B can be illustrated in the Roster form:
If A = {5, 6, 7, 8} and B = {7, 8, 9, 10} then A ∩ B = {7, 8}

→ Disjoint set: Consider A and B are two finite sets and if there are no common element in both A and B. Such set is known as disjoint set (or A ∩ B = ∅).
(or)
Two sets (finite) are said to be disjoint sets if they have no common elements. That is if the intersection of two sets is a null set they are disjoint sets.

→ The disjoint sets can be represented by means of the Venn diagrams as shown in the adjacent figure.

→ Difference of sets: The difference of sets A and B is the set of elements which belong to ‘A’ but do not belong to ‘B’.

→ We denote the difference of A and B by A – B or simply “A minus B”.

→ Set builder form of A – B is (x : x ∈ A and ∉ B}

→ Venn-diagram of A – B is

→ Venn-diagram of B – A is

→ A – B ≠ B – A

→ Fundamental theorem on sets:
If A and B are any two sets then n (A ∪ B) = n (A) + n (B) – n (A ∩ B) where
n (A ∪ B) = number of elements in the set (A ∪ B), also called cardinal number of A ∪ B
n (A) = number of elements in the set A also called cardinal number of A
n (B) = number of elements in the set B also called cardinal number of B

Students can go through AP SSC 10th Class Maths Notes Chapter 1 Real Numbers to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 1 Real Numbers

→ “God made the integers. All else is the work of man” …… Leopold Kronecker

→ Euclid’s division lemma: Given positive integers a, b there exists unique pair of integers q and r satisfying
a = bq + r; 0 ≤ r < b
This result was first published / recorded in book VII of Euclid’s “The Elements”.

→ Euclid’s division algorithm is a technique to compute the Highest Common Factor (H.C.F) of two given numbers.
E.g: HCF of 80 and 130
130 = 80 × 1 + 50 80 = 50 × 1 + 30
50 = 30 × 1 + 20 30 = 20 × 1 + 10
20 = 10 × 2 + 0 and H.C.F = 10

→ Euclid’s division algorithm can also be extended to all integers.

→ Numbers which can be expressed in the form p/q, where q ≠ 0 and ‘p and q’ are integers are called rational numbers; represented by Q.
Q = { [latex]\frac{p}{q}[/latex] ; q ≠ 0; p, q ∈ Z} .

→ Every rational number can be expressed either as a terminating decimal or as a non-terminating recurring decimal.

→ Numbers which can’t be expressed in p/q form are called irrational numbers represented by S. You may notice that the first letter of surds is ‘S’.
Eg: √2, √3, √5, …….. etc,

→ The combined set of rationals and irrationals is called the set of Real numbers; represented by R.
R = Q ∪ S.

→ Diagramatic representation of the number system:

where N = the set of natural numbers; W = the set of whole numbers;
Z = the set of integers; Q = the set of rational numbers;
S = the set of irrational numbers ; R = the set of real numbers.

→ Fundamental Theorem of Arithmetic: Every composite number can be expressed as a product of primes uniquely, (i.e.,) if x is a composite number, then
x = [latex]p_{1}^{l} \cdot p_{2}^{m} \cdot p_{3}^{n}[/latex] …… where p₁, p₂, p₃, ….. are prime numbers and l, m, n, …… are natural numbers.
Eg: 420 = 2 × 210 = 2 × 2 × 105 = 2 × 2 × 3 × 35 = 2 × 2 × 3 × 5 × 7
i. e. 420 = 2² × 3¹ × 5¹ × 7¹ and the factorisation on the R.H.S is unique.
Note: R.H.S is called exponential form of 420.

→  To find the H.C.F. of two or more numbers:
Step (i): Express given numbers in their exponential form.
Step (ii): Take the common bases.
Step (iii): Assign the respective smallest exponent from their exponential forms.
Step (iv): Take the product of the above.
Eg: H.C.E of 60 and 75 is
Step (i) 60 = 2² × 3 × 5 ; 75 = 3 × 5²
Step (ii) 3^O × 5^O [taking common bases]
Step (iii) 3¹ × 5¹ [∵ smallest exponent among 3¹ and 3¹ is 1]
Step (iv) 3 × 5 = 15 [smallest exponent among 5¹ and 5² is 1]
∴ H.C.F = 15
(i.e.) The highest common factor of the given set of numbers is the product of the com¬mon bases with the respective least exponents.

→ To find the L.C.M. of two or more numbers:
Step – 1: Express the given numbers in their exponential forms.
Step – 2: Take every base.
Step – 3: Assign the respective greatest exponent to each base.
Step – 4: Take the product of the above.
Eg: L.C.M. of 60 and 75 is
Step – 1: 60 = 2² × 3 × 5 ; 75 = 3 × 5²
Step – 2: 2^O × 3^O × 5^O
Step – 3: 2² × 3¹ × 5²
Step – 4: 4 × 3 × 25 = 300
L.C.M = 300

→ We may notice that the product of any two numbers N₁ and N₂ is equal to the product of their L.C.M. (L) and H.C.F. (H).
i.e., N₁ . N₂ = L.H

→ Let x = p/q be a rational number. If the numerator p is divided by the denominator q, we get the decimal form of x. The decimal form of x may or may not be terminating, i.e., every rational number can be expressed either as a terminating decimal or a non-terminating decimal. This gives us the following theorems.
Theorem – 1: Let ‘x’ be a rational number when expressed in decimal form, terminates, then x can be expressed in the form p/q where p, q are co-primes and the prime factorization of q is of the form 2ⁿ × 5^m, where n and m are non-negative integers.
Theorem – 2: Let x = p/q be a rational number, where q is of the form 2ⁿ × 5^m then x has a decimal expansion that terminates.
Theorem – 3: Let x = p/q be a rational number, where p, q are co-primes and the prime factorization of q is not of the form 2ⁿ . 5^m (n, m ∈ Z⁺) then x has a decimal expansion which is non-terminating recurring decimal.
Theorem – 4: Let ‘p’ be a prime number. If p divides a² then p divides a, where ‘a’ is a positive integer.

→ If a is a non-zero rational number and b is any irrational number, then (a + b), (a – b), a/b and ab are all irrational numbers.

→ Properties of Real Numbers:
If a, b and c are any three real numbers we may notice that

• a + b is also a real number – closure property w.r.t. addition
  a.b is also a real number – closure property w.r.t. multiplication
• a + b = b + a – commutative property w.r.t. addition
  a . b = b . a – commutative property w.r.t. multiplication
• (a + b) + c = a + (b + c) – associative law w.r.t.
  addition (a.b).c = a.(b.c) – associative law w.r.t. multiplication
• a + 0 = 0 + a = a, where ‘0’ is the additive identity,
  a × 1 = 1 × a = a, where 1 is the multiplicative identity,
• a + (-a) = (-a) + a = 0 where (a) and (-a) are additive inverse of each other.
  a × [latex]\frac{1}{a}[/latex] = [latex]\frac{1}{a}[/latex] × a = 1 where a and [latex]\frac{1}{a}[/latex] are multiplicative inverse of each other.

→ If aⁿ = x, where a and x are positive integers and a ≠ 1, then we define log_ax = n read as logarithm of x to the base a is equal to n.
Eg.: 2⁴ = 16 ⇒ log₂16 = 4

→  log_ax + log_ay = log_axy

→ log_aa = 1

→ log_ax – log_ay = log_a[latex]\frac{x}{y}[/latex]

→ log_a1 = 0

→ log_ax^m = m log_ax

→ In general, the bases in the logarithms are 10 (or) e, where e’ is approximated to 2.718.

→ If p is a prime number and p divides a² then p divides ‘a’ also.

AP State Syllabus SSC 10th Class Maths Solutions 14th Lesson Statistics InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 14 Statistics InText Questions and Answers.

10th Class Maths 14th Lesson Statistics InText Questions and Answers

Think & Discuss

(Page No. 327)

Question 1.
The mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
Answer:
Mean calculated from ungrouped data is more accurate than, mean calculated from the grouped data. Since its calculation takes all the observations in the data into consideration.

Question 2.
When it is more convenient to use grouped data for analysis?
Answer:
Grouped data is convenient when the values f_i and x_i are low.

(Page No. 331)

Question 3.
Is the result obtained by all the three methods the same?
Answer:
Yes. Mean obtained by all the three methods are equal.

Question 4.
If x_i and f_i are sufficiently small, then which method is an appropriate choice?
Answer:
Direct method.

Question 5.
If x_i and f_i are numerically large numbers, then which methods are appropriate to use?
Answer:
Assumed – Mean method and Step – Deviation method.

Do these

(Page No. 334)

Question 1.
Find the mode of the following data.
a) 5, 6, 9, 10, 6, 12, 3, 6, 11, 10, 4, 6, 7.
Answer:
Mode = 6 (most repeated value of the data).

b) 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3.
Answer:
Mode = 3,7.

c) 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6.
Answer:
Mode = 2, 3, 4, 5, 6.

Question 2.
Is the mode always at the centre of the data?
Answer:
No. Mode may not beat the centre always.

Question 3.
Does the mode change, if another observation is added to the data in Example? Comment.
Answer:
In the example the observations are 0, 1, 2, 2, 2, 3, 3, 4, 5, 6.
Here mode = 2.
If we add ‘2’ then mode doesn’t change.
It we add ‘3’ then the mode will be ‘2’ and ‘3’.
Even if we add other then 3 the mode will not be changed.
So we cannot decide whether the mode changes or not. It depends on the situation.

Question 4.
If the maximum value of an observation in the data in Example 4 is changed to 8, would the mode of the data be affected? Comment.
Answer:
If the maximum value is altered to 8, the mode remains the same. Mode doesn’t consider the values but consider their frequencies only.

Think & Discuss

(Page No. 336)

Question 1.
It depends upon the demand of the situation whether we are interested in finding the average marks obtained by the students or the marks obtained by most of the students.
a) What do we find in the first situation?
Answer:
We find A.M.

b) What do we find in the second situation?
Answer:
We find the mode.

Question 2.
Can mode be calculated for grouped data with unequal class sizes?
Answer:
Yes. Mode can be calculated for grouped data with unequal class sizes.

AP State Syllabus SSC 10th Class Maths Solutions 13th Lesson Probability InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 13 Probability InText Questions and Answers.

10th Class Maths 13th Lesson Probability InText Questions and Answers

Do This

(Page No. 307)

Outcomes of which of the following experiments are equally likely ?
Question 1.
Getting a digit 1, 2, 3, 4, 5 or 6 when a die is rolled.
Answer:
Equally likely.

Question 2.
Picking a different colour ball from a bag of 5 red balls, 4 blue balls and 1 black ball.
Note: Picking two different colour balls …………..
i.e., picking a red or blue or black ball from a …………
Answer:
Not equally likely.

Question 3.
Winning in a game of carrom.
Answer:
Equally likely.

Question 4.
Units place of a two digit number selected may be 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9.
Answer:
Equally likely.

Question 5.
Picking a different colour ball from a bag of 10 red balls, 10 blue balls and 10 black balls.
Answer:
Equally likely.

Question 6.
a) Raining on a particular day of July.
Answer:
Not equally likely.

b) Are the outcomes of every experiment equally likely?
Answer:
Outcomes of all experiments need not necessarily be equally likely.

c) Give examples of 5 experiments that have equally likely outcomes and five more examples that do not have equally likely outcomes.
Answer:
Equally likely events:

1. Getting an even or odd number when a die is rolled.
2. Getting tail or head when a coin is tossed.
3. Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 10.
4. Drawing a green or black ball from a bag containing 8 green balls and 8 black balls.
5. Selecting a boy or girl from a class of 20 boys and 20 girls.
6. Drawing a red or black card from a deck of cards.

Events which are not equally likely:

1. Getting a prime or composite number when a die is thrown.
2. Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 5.
3. Getting a number which is a multiple of 3 or not a multiple of 3 from numbers 1, 2, …… 10.
4. Getting a number less than 5 or greater than 5.
5. Drawing a white ball or green ball from a bag containing 5 green balls and 8 white balls.

Question 7.
Think of 5 situations with equally likely events and find the sample space.    (Page No. 309)
Answer:
a) Tossing a coin: Getting a tail or head when a coin is tossed.
Sample space = {T, H}.
b) Getting an even or odd number when a die is rolled.
Sample space = (1, 2, 3, 4, 5, 6}.
c) Winning a game of shuttle.
Sample space = (win, loss}.
d) Picking a black or blue ball from a bag containing 3 blue balls and 3 blackballs = {blue, black}.
e) Drawing a blue coloured card or black coloured card from a deck of cards = {black, red}.

Question 8.
i) Is getting a head complementary to getting a tail? Give reasons.   (Page No. 311)
Answer:
Number of outcomes favourable to head = 1
Probability of getting a head = [latex]\frac{1}{2}[/latex] [P(E)]
Number of outcomes not favourable to head = 1
Probability of not getting a head = [latex]\frac{1}{2}[/latex] [P([latex]\overline{\mathrm{E}}[/latex])]
Now P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{1}{2}[/latex] + [latex]\frac{1}{2}[/latex] = 1
∴ Getting a head is complementary to getting a tail.

ii) In case of a die is getting a 1 comple-mentary to events getting 2, 3, 4, 5, 6? Give reasons for your answer.
Answer:
Yes. Complementary events.
∵ Probability of getting 1 = [latex]\frac{1}{6}[/latex] [P(E)]
Probability of getting 2, 3, 4, 5, 6 = P(E) = P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{5}{6}[/latex]
P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{1}{6}[/latex] + [latex]\frac{5}{6}[/latex] = [latex]\frac{6}{6}[/latex] = 1

iii) Write of five new pair of events that are complementary.
Answer:

1. When a dice is thrown, getting an even number is complementary to getting an odd number.
2. Drawing a red card from a deck of cards is complementary to getting a black card.
3. Getting an even number is complementary to getting an odd number from numbers 1, 2, ….. 8.
4. Getting a Sunday is complementary to getting any day other than Sunday in a week.
5. Winning a running race is complementary to loosing it.

Try This

Question 1.
A child has a dice whose six faces show the letters A, B, C, D, E and F. The dice is thrown once. What is the probability of getting (i) A? (ii) D?     (Page No. 312)
Answer:
Total number of outcomes (A, B, C, D, E and F) = 6.
i) Number of favourable outcomes to A = 1
Probability of getting A =
P(A) = [latex]\frac{\text { No.of favourable outcomesto } \mathrm{A}}{\text { No.of all possible outcomes }}[/latex] = [latex]\frac{1}{6}[/latex]

ii) No. of outcomes favourable to D = 1
Probability of getting D
= [latex]\frac{\text { No.of outcomes favourble to } \mathrm{D}}{\text { All possible outcomes }}[/latex] = [latex]\frac{1}{6}[/latex]

Question 2.
Which of the following cannot be the probability of an event?     (Page No. 312)
(a) 2.3
(b) -1.5
(c) 15%
(d) 0.7
Answer:
a) 2.3 – Not possible
b) -1.5 – Not possible
c) 15% – May be the probability
d) 0.7 – May be the probability

Question 3.
You have a single deck of well shuffled cards. Then, what is the probability that the card drawn will be a queen?     (Page No. 313)
Answer:
Number of all possible outcomes = 4 × 13 = 1 × 52 = 52
Number of outcomes favourable to Queen = 4 [♥ Q, ♦ Q, ♠ Q, ♣ Q]
∴ Probability P(E) = [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{4}{52}[/latex] = [latex]\frac{1}{13}[/latex]

Question 4.
What is the probability that it is a face card?     (Page No. 314)
Answer:
Face cards are J, Q, K.
∴ Number of outcomes favourable to face card = 4 × 3 = 12
No. of all possible outcomes = 52
P(E) = [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{12}{52}[/latex] = [latex]\frac{3}{13}[/latex]

Question 5.
What is the probability that it is a spade?       (Page No. 314)
Answer:
Number of spade cards = 13
Total number of cards = 52
Probability
= [latex]\frac{\text { Number of outcomes favourable to spades }}{\text { Number of all outcomes }}[/latex]
= [latex]\frac{13}{52}[/latex] = [latex]\frac{1}{4}[/latex]

Question 6.
What is the probability that is the face card of spades?       (Page No. 314)
Answer:
Number of outcomes favourable to face cards of spades = (K, Q, J) = 3
Number of all outcomes = 52
P(E) = [latex]\frac{3}{52}[/latex]

Question 7.
What is the probability it is not a face card?       (Page No. 314)
Answer:
Probability of a face card = [latex]\frac{12}{52}[/latex] from (1)
∴ Probability that the card is not a face card

(or)
Number of favourable outcomes = 4 × 10 = 40
Number of all outcomes = 52
∴ Probability
= [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{40}{52}[/latex] = [latex]\frac{10}{13}[/latex]

Think & Discuss

(Page No. 312)

Question 1.
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of any game?
Answer:
Probability of getting a head is [latex]\frac{1}{2}[/latex] and of a tail is [latex]\frac{1}{2}[/latex] are equal.
Hence tossing a coin is a fair way.

Question 2.
Can [latex]\frac{7}{2}[/latex] be the probability of an event? Explain.
Answer:
[latex]\frac{7}{2}[/latex] can’t be the probability of any event.
Since probability of any event should lie between 0 and 1.

Question 3.
Which of the following arguments are correct and which are not correct? Give reasons.
i) If two coins are tossed simultaneously, there are three possible outcomes – two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is [latex]\frac{1}{3}[/latex].
Answer:
False.
Reason:
All possible outcomes are 4
HH, HT, TH, TT
Thus, probability of two heads = [latex]\frac{1}{4}[/latex]
Probability of two tails = [latex]\frac{1}{4}[/latex]
Probability of one each = [latex]\frac{2}{4}[/latex] = [latex]\frac{1}{2}[/latex].

ii) If a dice is thrown, there are two possible outcomes – an odd number or an even number. Therefore, the probability of getting an odd number is [latex]\frac{1}{2}[/latex].
Answer:
True.
Reason:
All possible outcomes = (1, 2, 3, 4, 5, 6) = 6
Outcomes favourable to an odd number (1, 3, 5) = 3
Outcomes favourable to an even number = (2, 4, 6) = 3
∴ Probability (odd number)
= [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{3}{6}[/latex] = [latex]\frac{1}{2}[/latex].

AP State Syllabus SSC 10th Class Maths Solutions 12th Lesson Applications of Trigonometry InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 12 Applications of Trigonometry InText Questions and Answers.

10th Class Maths 12th Lesson Applications of Trigonometry InText Questions and Answers

Do This

(Page No. 297)

Question 1.
Draw diagram for the following situations:
i) A person is flying a kite at an angle of elevation a and the length of thread from his hand to kite is ‘l’.
ii) A person observes two banks of a river at angles of depression θ₁ and θ₂ (θ₁ < θ₂) from the top of a tree of height ‘h’ which is at a side of the river. The width of the river is ‘d’.
Answer:

In the figure
‘D’ is the position of person
CD is the height of the tree
AB is the width of the river
Angles of depression are θ₁ and θ₂.

Think & Discuss

(Page No. 297)

Question 1.
You are observing top of your school building at an angle of elevation a from a point which is at d meter distance from foot of the building. Which trigonometric ratio would you like to consider to find the height of the building?
Answer:

The trigonometric ratio which connects d and h is tan α.

Question 2.
A ladder of length x meter is leaning against a wall making angle θ with the ground. Which trigonometric ratio would you like to consider to find the height of the point on the wall at which the ladder is touching?
Answer:

We use ‘sin θ’ as it is the ratio between the side opp. to θ and hypotenuse.

AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry InText Questions and Answers.

10th Class Maths 11th Lesson Trigonometry InText Questions and Answers

Do This

Identify “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles.  (Page No. 271)

Question 1.
For angle R
Answer:

In the △PQR
Opposite side = PQ
Adjacent side = QR
Hypotenuse = PR

Question 2.
i) For angle X
ii) For angle Y        (Page No. 271)
Answer:

In the △XYZ,
i) For angle X
Opposite side = YZ
Adjacent side = XZ
Hypotenuse = XY
ii) For angle Y
Opposite side = XZ
Adjacent side = YZ
Hypotenuse = XY

Question 3.
Find (i) sin C (ii) cos C and (iii) tan C in the given triangle.    (Page No. 274)

Answer:
By Pythagoras theorem
AC² = AB² + BC²
13² = AB² + 5²
AB² = 169 – 25
AB² = √144
⇒ AB = √144 = 12

Question 4.
In a triangle XYZ, ∠Y is right angle, XZ = 17 cm and YZ = 15 cm, then find (i) sin X (ii) cos Z (iii) tan X.    (Page No. 274)
Answer:
Given △XYZ, ∠Y is right angle.

By Pythagoras theorem
XZ² = YZ² + XY²
17² = 15² + XY²
XY² = 17² – 15² = 289 – 225
XY² = 64
XY = √64 = 8

Question 5.
In a triangle PQR with right angle at Q, the value of ∠P is x, PQ = 7 cm and QR = 24 cm, then find sin x and cos x.    (Page No. 274)
Answer:
Given right angled triangle is PQR with right angle at Q. The value of ∠P is x.

By Pythagoras theorem
PR² = PQ² + QR²
PR² = 7² + 24²
PR² = 49 + 576
PR² = 625
PR² = √625 = 25
sin x = [latex]\frac{QR}{PR}[/latex] = [latex]\frac{24}{25}[/latex]
cos x = [latex]\frac{PQ}{PR}[/latex] = [latex]\frac{7}{25}[/latex]

Try This

Question 1.
Write lengths of “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles.
1. For angle C
2. For angle A          (Page No. 271)
Answer:

By Pythagoras theorem
AC² = AB² + BC²
(5)² = AB² + 4²
25 = AB² + 16
AB² = 25 – 16
AB² = 9
AB = √9 = 3
For angle C:
Opposite side = AB = 3 cm
Adjacent side = BC = 4 cm
Hypotenuse = AC = 5 cm
For angle A:
Opposite side = BC = 4 cm
Adjacent side = AB = 3 cm
Hypotenuse = AC = 5 cm

Question 2.
In a right angle triangle ABC, right angle is at C. BC + CA = 23 cm and BC – CA = 7 cm, then find sin A and tan B.    (Page No. 274)
Answer:
In a right angle triangle ABC, right angle is at C.

BC = [latex]\frac{30}{2}[/latex] = 15
BC = 15
Substituting BC = 15 in equation (1)
BC + CA = 23
CA = 23 – BC = 23 – 15
CA = 8
By Pythagoras theorem
AB² = AC² + BC²
= 8² + 15²
= 64 + 225 = 289
= √289 = 17
sin A = [latex]\frac{BC}{AB}[/latex] = [latex]\frac{15}{17}[/latex]
cos B = [latex]\frac{AC}{BC}[/latex] = [latex]\frac{8}{15}[/latex]

Question 3.
What will be the ratios of sides for sec A and cot A?    (Page No. 275)
Answer:
sec A = [latex]\frac{\text { Hypotenuse }}{\text { Adjacent side of the angle } \mathrm{A}}[/latex]
cot A = [latex]\frac{\text { Adjacent side of the angle } A}{\text { Opposite side of the angle } A}[/latex]

Think & Discuss

Question 1.
Discuss with your friends
i) sin x = [latex]\frac{4}{3}[/latex] does exist for some value of angle x?
ii) The value of sin A and cos A is always less than 1. Why?
iii) tan A is product of tan and A.        (Page No. 274)
Answer:
i) The value of sin 0 always lies between 0 and 1. Here sin x = [latex]\frac{4}{3}[/latex] which is greater than 1. So, it does not exist.
ii)

We observe in above sin A, cos A, hypotenuse is in denominator which is greater than other two sides
∴ sin A = [latex]\frac{\text { Opposite side }}{\text { Hypotenuse }}[/latex] = [latex]\frac{Nr}{Dr}[/latex]
here denominator is more than numerator. Hence its value will be less than 1.
cos A = [latex]\frac{\text { Adjacent side }}{\text { Hypotenuse }}[/latex]
here also adjacent side is always less than hypotenuse. Hence its value is also less than or equal to 1.

iii) The symbol tan A is used as an abbreviation for “the tan of the angle A”.
tan A is not the product of “tan” and A. “tan” separated from A’ has no meaning.

Question 2.
Is [latex]\frac{\sin \mathrm{A}}{\cos \mathrm{A}}[/latex] equal to tan A?      (Page No. 275)
Answer:
Yes, [latex]\frac{\sin \mathrm{A}}{\cos \mathrm{A}}[/latex] = tan A
Proof:

Question 3.
Is [latex]\frac{\cos \mathrm{A}}{\sin \mathrm{A}}[/latex] equal to cot A?     (Page No. 275)
Answer:
Yes, [latex]\frac{\cos \mathrm{A}}{\sin \mathrm{A}}[/latex] = tan A
Proof:

cot A = [latex]\frac{\text { Adjacent side }}{\text { Opposite side }}[/latex]

Do this

Question 1.
Find cosec 60°, sec 60° and cot 60°.       (Page No. 279)
Answer:

Consider an equilateral triangle ABC. Since each angle is 60° in an equilateral triangle, we have ∠A = ∠B = ∠C = 60° and the sides of equilateral triangle is AB = BC = CA = 2a units.
Draw the perpendicular line AD from vertex A to BC as shown in the given figure.
Perpendicular AD acts as “angle bisector of angle A” and “bisector of the side BC” in the equilateral triangle ABC.
Therefore, ∠BAD = ∠CAD = 30°. Since point D divides the side BC into equal halves.
BD = [latex]\frac{1}{2}[/latex] BC = [latex]\frac{2a}{2}[/latex] = a units.
Consider right angle triangle ABD in the above given figure.
We have AB = 2a and BD = a
Then AD² = AB² – BD²
(By Pythagoras theorem)
= (2a)² – (a)² = 3a²
Therefore, AD = a√3
From definitions of trigonometric ratios,

Try this

Question 1.
Find sin 30°, cos 30°, tan 30°, cosec 30°, sec 30° and cot 30° by using the ratio concepts.     (Page No. 279)
Answer:

Consider an equilateral triangle ABC. Since each angle is 60° in an equilateral triangle, we have ∠A = ∠B = ∠C = 60° and the sides of equilateral triangle is AB = BC = CA = 2a units.
Draw the perpendicular line AD from vertex A to BC as shown in the given figure.
Perpendicular AD acts as “angle bisector of angle A” and “bisector of the side BC” in the equilateral triangle ABC.
Therefore, ∠BAD = ∠CAD = 30°. Since point D divides the side BC into equal halves.
BD = [latex]\frac{1}{2}[/latex] BC = [latex]\frac{2a}{2}[/latex] = a units.
Consider right angle triangle ABD in the above given figure.
We have AB = 2a and BD = a
Then AD² = AB² – BD²
(By Pythagoras theorem)
= (2a)² – (a)² = 3a²
Therefore, AD = [latex]\sqrt{3 a^{2}}[/latex] = √3a
BD = a, AD = √3a and hypotenuse = AB = 2a and ∠DAB = 30°.
sin 30° = [latex]\frac{BD}{AB}[/latex] = [latex]\frac{a}{2a}[/latex] = [latex]\frac{1}{2}[/latex]

Question 2.
Find the values for tan 90°, cosec 90°, sec 90° and cot 90°.     (Page No. 281)
Answer:
From the adjacent figure, the trigonometric ratios of ∠A, gets larger and larger in △ABC till it becomes 90°.

As ∠A get larger and larger, ∠C gets smaller and smaller. Therefore, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠A is very close to 90°, ∠C becomes very close to 0° and the side AC almost coincides with side BC.

∴ AB = 0 and AC = BC = r
From trigonometric ratios
sin A = [latex]\frac{BC}{AC}[/latex]
sin A = [latex]\frac{AB}{AC}[/latex]
If A = 90°, then AB = 0 and AC = BC = r,

Think & Discuss

Question 1.
Discuss with your friend about the following conditions:
What can you say about cosec 0° = [latex]\frac{1}{\sin 0^{\circ}}[/latex]? Is it defined? Why?    (Page No. 280)
Answer:
sin 0° = 0
cosec 0° = [latex]\frac{1}{\sin 0^{\circ}}[/latex] = [latex]\frac{1}{0}[/latex] = not defined.
It is not defined.
Reason:
Division by ‘0’ is not allowed, hence [latex]\frac{1}{0}[/latex] is indeterminate.

Question 2.
What can you say about cot 0° = [latex]\frac{1}{\tan 0^{\circ}}[/latex]. Is it defined? Why?    (Page No. 281)
Is it defined? Why?
Answer:
tan 0° = 0
cot 0° = [latex]\frac{1}{\tan 0^{\circ}}[/latex] = [latex]\frac{1}{0}[/latex] = undefined.
Reason:
Division by ‘0’ is not allowed, hence [latex]\frac{1}{0}[/latex] is indeterminate.

Question 3.
sec 0° = 1. Why?      (Page No. 281)
Answer:
sec 0° = [latex]\frac{1}{\cos 0^{\circ}}[/latex] [∵ cos 0° = 1]
= [latex]\frac{1}{1}[/latex] = 1

Question 4.
What can you say about the values of sin A and cos A, as the value of angle A increases from 0° to 90°? (Observe the above table)
i) If A ≥ B, then sin A ≥ sin B. Is it true?
ii) If A ≥ B, then cos A ≥ cos B. Is it true? Discuss.      (Page No. 282)
Answer:
i) Given statement
“If A ≥ B, then sin A ≥ sin B”
Yes, this statement is true.
Because, it is clear from the table below that the sin A increases as A increases.

ii) Given statement
“If A ≥ B, then cos A ≥ cos B”
No, this statement is not true.
Because, it is clear from the table below that cos A decreases as A increases.

Think & Discuss

Question 1.
For which value of acute angle
(i) [latex]\frac{\cos \theta}{1-\sin \theta}[/latex] + [latex]\frac{\cos \theta}{1+\sin \theta}[/latex] = 4 is true?
For which value of 0° ≤ θ ≤ 90°, above equation is not defined?    (Page No. 285)
Answer:


⇒ cos θ = cos 60° [from trigonometric ratios table]
⇒ θ = 60°
Given statement is true for the acute angle i.e., θ = 60°.

Question 2.
Check and discuss the above relations in the case of angles between 0° and 90°, whether they hold for these angles or not? So,          (Page No. 286)
i) sin (90° – A) = cos A
ii) cos (90° – A) = sin A
iii) tan (90° – A) = cot A and
iv) cot (90° – A) = tan A
v) sec (90° – A) = cosc A
vi) cosec (90° – A) = sec A
Answer:
Let A = 30°
i) sin (90° – A) = cos A
⇒ sin (90° – 30°) = cos 30°
⇒ sin 60° = cos 30° = [latex]\frac{\sqrt{3}}{2}[/latex]

ii) cos (90° – A) = sin A
⇒ cos (90° – 30°) = sin 30°
⇒ cos 60° = sin 30° = [latex]\frac{1}{2}[/latex]

iii) tan (90° – A) = cot A
⇒ tan (90° – 30°) = cot 30°
⇒ tan 60° = cot 30° = √3

iv) cot (90° – A) = tan A
⇒ cot (90° – 30°) = tan 30°
⇒ cot 60° = tan 30° = [latex]\frac{1}{\sqrt{3}}[/latex]

v) sec (90° – A) = cosec A
⇒ sec (90° – 30°) = cosec 30°
⇒ sec 60° = cosec 30° = 2

vi) cosec (90° – A) = sec A
⇒ cosec (90° – 30°) = sec 30°
⇒ cosec 60° = sec 30° = [latex]\frac{2}{\sqrt{3}}[/latex]

So, the above relations hold for all the angles between 0° and 90°.

Do this

(Page No. 290)

Question 1.
i) If sin A = [latex]\frac{15}{17}[/latex] then find cos A.
Answer:
Given sin A = [latex]\frac{15}{17}[/latex]
cos A = [latex]\sqrt{1-\sin ^{2} A}[/latex] [From Identity -I]

ii) If tan x = [latex]\frac{5}{12}[/latex], then find sec x. (AS j)
Answer:
Given tan x = [latex]\frac{5}{12}[/latex]
We know that sec² x – tan² x = 1
sec² x = 1 + tan² x

iii) If cosec θ = [latex]\frac{25}{7}[/latex], then find cot θ.
Answer:
Given cosec θ = [latex]\frac{25}{7}[/latex]
We know that cosec² θ – cot² θ = 1
cot² θ = cosec² θ – 1

Try This

(Page No. 290)

Question 1.
Evaluate the following and justify your answer.

i) [latex]\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}[/latex]
Answer:
Given [latex]\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}[/latex]

[∵ sin (90° – θ) = cos θ; cos (90° – θ) = sin θ]
= [latex]\frac{1}{1}[/latex] = 1 [By sin² θ + cos² θ = 1]

ii) sin 5° cos 85° + cos 5° sin 85°
Answer:
Given sin 5° cos 85° + cos 5° sin 85°
= sin 5° . cos (90° – 5°) + cos 5° . sin (90° – 5°)
= sin 5° . sin 5° + cos 5° . cos 5°
[∵ sin (90° – θ) = cos θ; cos (90° – θ) = sin θ]
= sin² 5° + cos² 5°
= 1 [∵ sin² θ + cos² θ = 1]

iii) sec 16° cosec 74° – cot 74° tan 16°.
Answer:
Given sec 16° cosec 74° – cot 74° tan 16°
= sec 16° . cosec (90° – 16°) – cot (90° – 16°) . tan 16°
= sec 16°. sec 16° – tan 16° . tan 16° [∵ cosec (90° – θ) = sec θ; cot (90° – θ) — tan θ]
= sec² 16° – tan² 16°
= 1 [∵ sec² θ – tan² θ = 1]

Think & Discuss

(Page No. 290)

Question 1.
Are these identities true for 0° ≤ A ≤ 90°? If not for which values of A they are true?
i) sec² A – tan² A = 1
Answer:
Given identity is sec² A – tan² A = 1
Let A = 0°
L.H.S. = sec² 0° – tan² 0°
= 1 – 0 = 1 = R.H.S.
Let A = 90°
tan A and sec A are not defined.
So it is true.
∴ For all given values of ‘A’ such that 0° ≤ A ≤ 90° this trigonometric identity is true.

ii) cosec² A – cot² A = 1
Answer:
Given identity is cosec² A – cot² A = 1
Let A = 0°
cosec A and cot A are not defined for A = 0°.
Therefore identity is true for A = 0°.
Let A = 90°
cosec A = cosec 90° = 1
cot A = cot 90° = 0
L.H.S. = l² – 0² = 1 – 0 = 1 = R.H.S.
∴ This identity is true for all values of A, such that 0° ≤ A ≤ 90°.

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration InText Questions and Answers.

10th Class Maths 10th Lesson Mensuration InText Questions and Answers

Try this

(Page No. 245)

Question 1.
Consider the following situations. In each find out whether you need volume or area and why?
i) Quantity of water inside a bottle.
ii) Canvas needed for making a tent.
iii) Number of bags inside the lorry.
iv) Gas filled in a cylinder.
v) Number of match sticks that can be put in the match box.
Answer:
i) Volume: 3-d shape
ii) Area: L.S.A. / T.S.A.
iii) Volume: 3-d shape
iv) Volume: 3-d shape
v) Volume: 3-d shape

Question 2.
Write 5 more such examples and ask your friends to choose what they need?
Answer:
Student’s Activity.

Question 3.
Break the pictures in the previous figure into solids of known shapes.    (Page No. 246)
Answer:

Question 4.
Think of 5 more objects around you that can be seen as a combination of shapes. Name the shapes that combined to make them.    (Page No. 246)
Answer:
Student’s Activity.

Try this

Question 1.
Use known solid shapes and make as many objects (by combining more than two) as possible that you come across in your daily life.
[Hint: Use clay, or balls, pipes, paper cones, boxes like cube, cuboid etc]      (Page No. 252)
Answer:
Student’s Activity.

Think & Discuss

Question 1.
A sphere is inscribed in a cylinder. Is the surface of the sphere equal to the curved surface of the cylinder? If yes, explain how.      (Page No. 252)

Answer:
Yes, the surface area of the sphere is equal to the curved surface area of the cylinder.
Let the radius of the “cylinder be ‘r’ and its height ‘h’.
Then radius of sphere = r.
Then curved surface area of cylinder = 2πrh = 2πr (r + r)
[∵ height = diameter of the sphere = diameter of the cylinder = 2r]
= 2πr (2r) = 4πr²
And surface area of the sphere = 4πr²
∴ C.S.A. of cylinder = Surface area of sphere.

Try This

(Page No. 257)

Question 1.
If the diameter of the cross – section of a wire is decreased by 5%, by what percentage should the length be increased so that the volume remains the same ?
Answer:
Let the radius of wire = r
(if diameter = 2r)
and length of wire = h = l (say)
then volume of wire = πr²l₁ = v₁ ….(1)
Now the diameter after decreasing 5%

then radius of wire after decreasing
= [latex]\frac{190r}{100}[/latex] × [latex]\frac{1}{2}[/latex] = [latex]\frac{95r}{100}[/latex]
and let the length of wire = (l₂)

So it length is increased by 24.22%. Its volume remains same.

Question 2.
Surface area of a sphere and cube are equal. Then find the ratio of their volumes.
Answer:
Let a cube with side ‘a’.
Then its surface area = 6a²
By problem, surface area of the sphere = 4πr²
Surface area of the cube = 6a²

Do This

(Page No. 263)

Question 1.
A copper rod of diameter 1 cm. and length 8 cm; is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Answer:
Volume of the copper rod (cylinder)
= πr²h
= [latex]\frac{22}{7}[/latex] × [latex]\frac{1}{2}[/latex] × [latex]\frac{1}{2}[/latex] × 8
= [latex]\frac{44}{7}[/latex] m²
If V is the radius of the wire, then its volume = πr²h
∴ The volume of rod is equal to the volume of the wire. We have

∴ Thickness = d = 2 × 0.03 ≃ 0.06 cm.

Question 2.
Pravali house has a water tank in the shape of a cylinder on the roof. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 9.5 cm. The water tank has radius 60 cm. and height 95 cm. Find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Compare the capacity of the tank with that of the sump, (π = 3.14)
Answer:
Volume of the water in the sump = 1.57 × 1.44 × 0.95 [∵ V = lbh]
= 2.14776 m³ = 2147760 cm³
Volume of the tank on the roof = πr²h
= 3.14 × 60 × 60 × 95
= 1073880 cm³
∴ Volume of the water left in the sump after filling the tank
= 2147760 – 1073880 = 1073880 cm³
Let the height of the water in the tank be h.
∴ 157 × l44h = 1073880
h = [latex]\frac{1073880}{157 \times 144}[/latex] = 47.5 cm.
∴ Ratio of the volume of the sump and tank = 2147760 : 1073880 = 2 : 1
∴ Sump can hold two times the water that can be hold in the tank.

Think & Discuss

(Page No. 262)

Question 1.
Which barrel shown in the below figure can hold more water? Discuss with your friends.

Answer:
r₁ = [latex]\frac{1}{2}[/latex] = 0.5 cm; h₁ = 4 cm
Volume of the 1st barrel = πr²h
= [latex]\frac{22}{7}[/latex] × 0.5 × 0.5 × 4 = 3.142 cm³
r₂ = [latex]\frac{4}{2}[/latex] = 2 cm
∴ h = 1 cm
Volume of the 2nd barrel
V = πr²h = [latex]\frac{22}{7}[/latex] × 2 × 2 × 1 = 12.57 cm³
Hence the volume of the 2nd barrel is more than the first barrel.

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle InText Questions and Answers.

10th Class Maths 9th Lesson Tangents and Secants to a Circle InText Questions and Answers

Do this

Question 1.
Draw a circle with any radius. Draw four tangents at different points. How many tangents can you draw to this circle?    (Page No. 226)
Answer:

Let ‘O’ be the centre of the circle with radius OA.
l, m, n, p and q be the tangents to the circles at A, B, C, D and E. We can draw a tangent at each point on the circle, i.e., infinitely many tangents can be drawn to a circle.

Question 2.
How many tangents you can draw to circle from a point away from it?    (Page No. 226)
Answer:

We can draw only two tangents from an exterior point.

Question 3.
In the below figure which are tangents to the given circles?      (Page No. 226)

Answer:
P and M are the tangents to the given circles.

Question 4.
Draw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it. What happens to the length of chord coming closer and closer to the centre of the circle?      (Page No. 227)

Answer:

The length of the chord increases as it comes closer to the centre of the circle.

Question 5.
What is the longest chord?        (Page No. 227)
Answer:
Diameter is the longest of all chords.

Question 6.
How many tangents can you draw to a circle, which are parallel to each other?    (Page No. 227)
Answer:
Only one tangent can be drawn parallel to a given tangent.
To a circle, we can draw infinitely many pairs of parallel tangents.

Try this

(Page No. 228)

How can you prove the converse of the above theorem.
Question 1.
“If a line in the plane of a circle is perpendicular to the radius at its end point on the circle, then the line is tangent to the circle”.
Answer:
Given: Circle with centre ‘O’, a point A on the circle and the line AT perpendicular to OA.
R.T.P: AT is a tangent to the circle at A.
Construction:

Suppose AT is not a tangent then AT produced either way if necessary, will meet the circle again. Let it do so at P, join OP.
Proof: Since OA = OP (radii)
∴ ∠OAP = ∠OPA But ∠OPA = 90°
∴ Two angles of a triangle are right angles which is impossible.
∴ Our supposition is false.
∴ Hence AT is a tangent.

We can find some more results using the above theorem.
i) Since there can be only one perpendicular OP at the point P, it follows that one and only one tangent can be drawn to a circle at a given point on the circumference.
ii) Since there can be only one perpendicular to XY at the point P, it follows that the perpendicular to a tangent at its point of contact passes through the centre.

Question 2.
How can you draw the tangent to a circle at a given point when the centre of the circle is not known?    (Page No. 229)
Answer:

Steps of Construction:

1. Take a point P and draw a chord PR through P.
2. Construct ∠PRQ and measure it.
3. Construct ∠QPX at P equal to ∠PRQ.
4. Extend PX on other side. XY is the required tangent at P.

Note: Angle between a tangent and chord is equal to angle in the alternate segment.

Hint: Draw equal angles ∠QPX and ∠PRQ. Explain the construction.
Answer:

Steps of construction:

1. Draw any two chords AB and AC in the given circle.
2. Draw the perpendicular bisectors to AB and AC, they meet at the centre of the circle.
3. Tet O be the centre, join OP.
4. Draw a perpendicular to OP at P and extend it on either sides which forms a tangent to the circle at ‘P’.

Try this

Question 1.
Use Pythagoras theorem and write proof of above theorem “the lengths of tangents drawn from an external point to a circle are equal.”      (Page No. 231)
Answer:
Given: Two tangents PA and PB to a circle with centre O, from an exterior point P.
R.T.P: PA = PB

Proof: In △OAP; ∠OAP = 90°
∴ AP² = OP² – OA²
[∵ Square of the hypotenuse is equal to the sum of squares on the other two sides – Pythagoras theorem]
[∵ OA = OB, radii of the same circle]
= BP² [∵ In AOBP; OB² + BP² = OP²
⇒ BP² – OP² – OB²]
⇒ AP² – BP²
⇒ PA – PB Hence proved.

Question 2.
Draw a pair of radii OA and OB such that ∠BOA = 120°. Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and justify.    (Page No. 235)
Answer:

Justification:
OA ⊥ PA
OB ⊥ PB
Also in △OAP, △OBP
OA = OB
∠OAP = ∠OBP
OP – OP
∴ △OAP ≅ △OBP
∴ PA = PB. [Q.E.D.]

Do this

Question 1.
Shankar made the following pictures also with washbasin.

What shapes can they be broken into that we can find area easily?    (Page No. 237)
Answer:

Question 2.
Make some more pictures and think of the shapes they can be divided into different parts.      (Page No. 237)
Answer:

Question 3.
Find the area of sector, whose radius is 7 cm. with the given angles.    (Page No. 239)
i) 60° ii) 30° iii) 72° iv) 90° v) 120°
Answer:

Question 4.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 10 minutes.    (Page No. 239)
Answer:
Angle made by minute hand in 1 m = [latex]\frac{360^{\circ}}{60}[/latex] = 6°
Angle made by minute hand in 10m = 10 × 6 = 60°
The area swept by minute hand is in the shape of a sector with radius r = 14 cm and angle x = 60°

Area swept by the minute hand in 10 minutes = 102.66 cm².

Try this

Question 1.
How can you find the area of major segment using area of minor segment?    (Page No. 239)
Answer:

Area of the major segment = Area of the circle – Area of the minor segment.