Category: AP State Important Questions

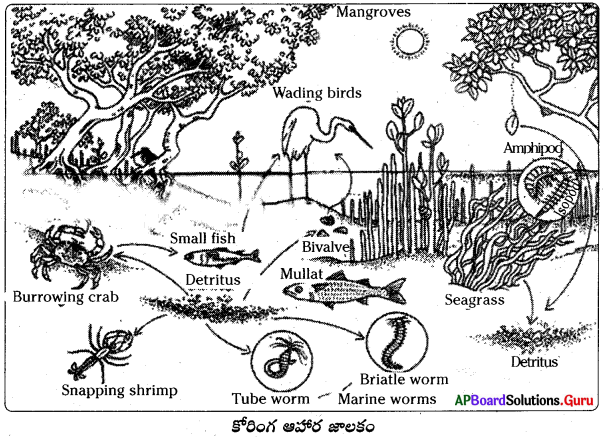
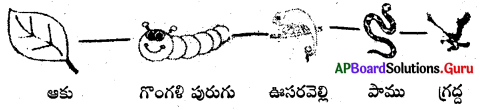
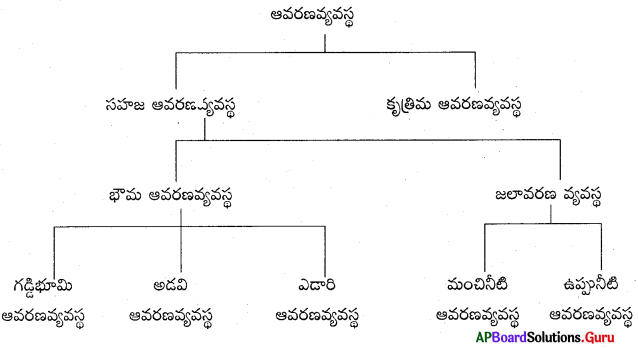
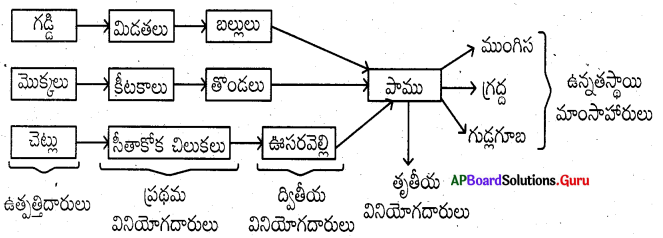
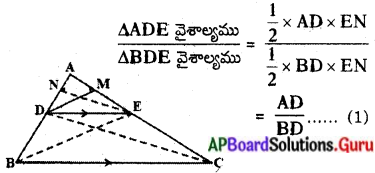
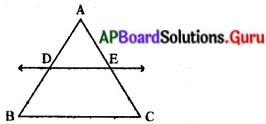
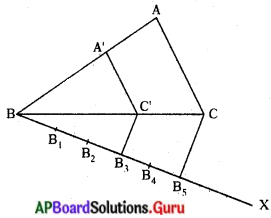
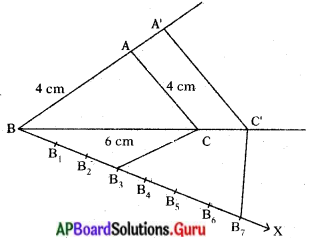
These AP 10th Class Maths Chapter Wise Important Questions 14th Lesson సాంఖ్యక శాస్త్రం will help students prepare well for the exams

AP Board 10th Class Maths 14th Lesson Important Questions and Answers సాంఖ్యక శాస్త్రం

ప్రశ్న 1.
5, 3, 4, – 4, 6, 7, 0 దత్తాంశ మధ్యగతము ఎంత?
సాధన.
ఇవ్వబడిన పరిశీలనాంశములు 5, 3, 4, – 4, 6, 7, 0.
పరిశీలనాంశములను ఆరోహణ క్రమంలో వ్రాయగా – 4, 0, 3, 4, 5, 6, 7.
మొత్తము 7 పరిశీలనాంశములున్నవి. కనుక [latex]\frac{7+1}{2}[/latex] = 4వ పరిశీలనాంశము మధ్యగతమగును.
∴ మధ్యగతము = 3.

ప్రశ్న 2.
5, 6, 9, 6, 12, 3, 6, 11, 6, 7 ల బాహుళకం ఎంత ?
సాధన.
5, 6, 9, 6, 12, 3, 6, 11, 6, 7 లలో 6 యొక్క పౌనఃపున్యము గరిష్టం కావున పై దత్తాంశానికి బాహుళకం = 6.

ప్రశ్న 3.
మొదటి n సహజ సంఖ్యల సగటు కనుగొనుము.
సాధన.
సగటు = మొదటి ‘n’ సహజ సంఖ్యల మొత్తం / n
= [latex]\frac{\Sigma \mathrm{n}}{\mathrm{n}}=\frac{\mathrm{n}(\mathrm{n}+1)}{2} \cdot \frac{1}{\mathrm{n}}=\left[\frac{\mathrm{n}+1}{2}\right][/latex]
∴ మొదటి ‘n’ సహజ సంఖ్యల సగటు = [latex]\frac{n+1}{2}[/latex]

ప్రశ్న 4.
వర్గీకృత దత్తాంశము యొక్క అంకగణితపు సగటు [latex]\bar{x}=a+\frac{\sum f_{1} d_{i}}{\Sigma f_{i}}[/latex] అయిన f_i మరియు d_i పదాలు వేటిని సూచిస్తాయి ?
సాధన.
f_i = తరగతి పౌనఃపున్యం
d_i = విచలనము = x_i – a

ప్రశ్న 5.
5, 6, 9, 10, 6, 12, 3, 6, 11, 10 ల దత్తాంశపు సగటు ఎంత ?
సాధన.
దత్తాంశం సగటు = ఇచ్చిన రాశుల మొత్తం / ఇచ్చిన రాశుల సంఖ్య
= [latex]\frac{5+6+9+10+6+12+3+6+11+10}{10}[/latex]
= [latex]\frac{78}{10}[/latex] = 7.8.

ప్రశ్న 6.
క్రింది దత్తాంశానికి ఆరోహణ సంచిత మరియు అవరోహణ సంచిత పౌనఃపున్య పట్టికలు వ్రాయండి.

సాధన.
ఆరోహణ సంచిత పౌనఃపున్య పట్టిక

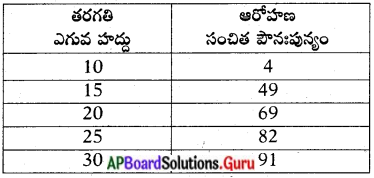
అవరోహణ సంచిత పౌనఃపున్య పట్టిక

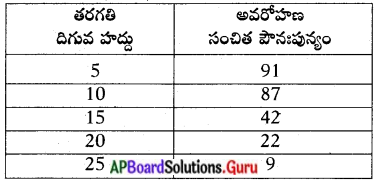
ప్రశ్న 7.
క్రింది పౌనఃపున్య విభాజన. పట్టికకు మధ్య విలువలు • వ్రాయండి.

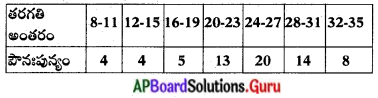
సాధన.

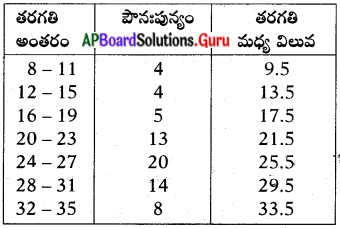
ప్రశ్న 8.
క్రింది దత్తాంశమునకు మధ్యగతమును కనుగొనుము.

సాధన.

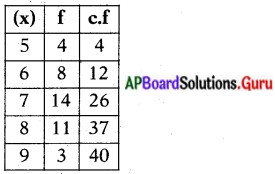
n = 40
మధ్యగతము = [latex]\frac{n+1}{2}=\frac{40+1}{2}=\frac{41}{2}[/latex] = 20.
5వ పదము = 7.

ప్రశ్న 9.
ఈ క్రింది దత్తాంశమునకు తరగతి అంతరములను ఉపయోగించి పౌనఃపున్య విభాజన పట్టికను తయారు చేయుము. .

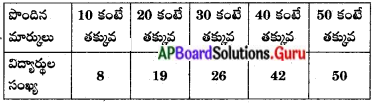
సాధన.

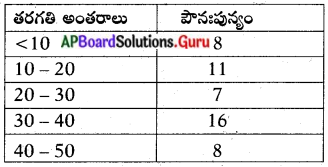
ప్రశ్న 10.
క్రింది దత్తాంశం యొక్క అంకమధ్యమాన్ని కనుగొనండి.

సాధన.

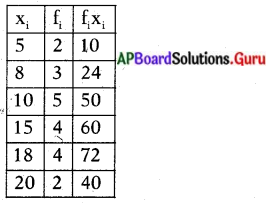
Σf_ix_i = 256; Σf_i = 20
అంకమధ్యమం = [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{256}{20}[/latex] = 12.8.

ప్రశ్న 11.
క్రింది దత్తాంశమునకు బాహుళకము కనుగొనండి.

సాధన.

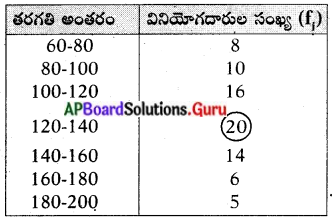
ఎక్కువ మంది వినియోగదారులు 120 – 140.
తరగతికి చెందినవారు కనుక బాహుళకపు తరగతి. 120 – 140.
బాహుళకపు తరగతి దిగువహద్దు (l) = 120
తరగతి పరిమాణము (h) = 20
బాహుళకపు తరగతి పౌనఃపున్యం (f₁) = 20
బాహుళకపు తరగతికి పూర్వపు తరగతి పౌనఃపున్యం (f₀) = 16.
బాహుళకపు తరగతికి తర్వాత పౌనఃపున్యం (f₂) = 14.
సూత్రమునుపయోగించి,
బాహుళకము = l + [latex]\left[\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right][/latex] × h

= 120 + [latex]\left[\frac{20-16}{2 \times 20-16-14}\right][/latex] × 20

= 120 + [latex]\left[\frac{4}{40-30}\right][/latex] × 20

= 120 + [latex]\left[\frac{4}{10}\right][/latex] × 20
= 120 + 8 = 128.

ప్రశ్న 12.
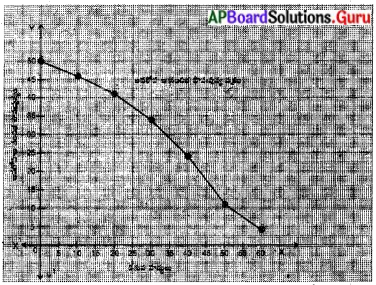
క్రింది దత్తాంశానికి “అవరోహణ సంచిత పౌనఃపున్య వక్రం” గీయండి.

సాధన.
అవరోహణ సంచిత పౌనఃపున్య వక్రం

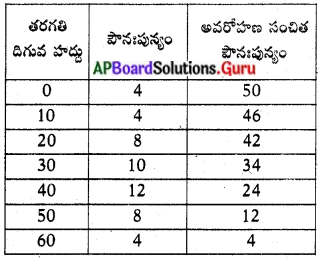
X- అక్షంపై దిగువ హద్దులు, మరియు Y – అక్షంపై అవరోహణ సంచిత పౌనఃపున్యం గుర్తించుము.

X- అక్షంపై 1 సెం.మీ. = 5 యూ.
Y – అక్షంపై 1 సెం.మీ. = 5 యూ.

ప్రశ్న 13.
క్రింది దత్తాంశమునకు బాహుళకము కనుక్కోండి. ”

సాధన.

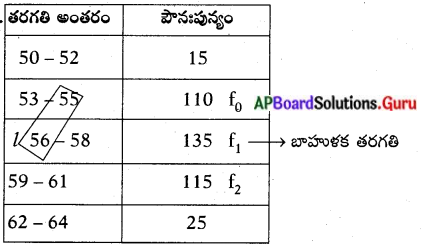
బాహుళకము = l + [latex]\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}[/latex] × h;
l = 55.5; f₀ = 110; f₁ = 135; f₂ = 115; h = 3

బాహుళకము = 55.5 + [latex]\frac{25}{270-225}[/latex] × 3

= 55.5 + [latex]\frac{25}{45}[/latex] × 3

= 55.5 + [latex]\frac{5}{3}[/latex] × 3

= 55.50 + 1.67 = 57.17.

ప్రశ్న 14.
దిగువనీయబడిన దత్తాంశమునకు ‘మధ్యగతము’ కనుగొనండి.

సాధన.

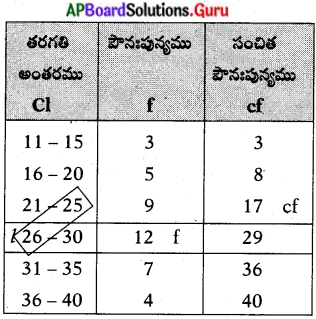
n = 40, [latex]\frac{n}{2}\frac{40}{2}[/latex] = 20
l = 25.5, f = 12, cf = 17, h = 5
మధ్యగతము = l + [latex]\left(\frac{\frac{n}{2}-c f}{f}\right)[/latex] × h
= 25.5 + ([latex]\frac{20-17}{12}[/latex]) × 5
= 25.5 + ([latex]\frac{3}{12}[/latex] × 5)
= 25.50 + [latex]\frac{5}{4}[/latex]
= 25.50 + 1.25 = 26.75.

ప్రశ్న 15.
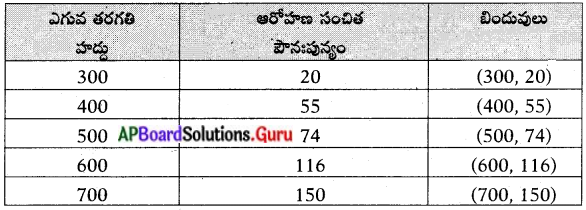
ఈ క్రింది పట్టికను, ఆరోహణ సంచిత పౌనఃపున్య పట్టికగా మార్చి దానినుపయోగించి ‘ఓజివ్’ వక్రమును గ్రాఫ్ ద్వారా చూపుము.

సాధన.

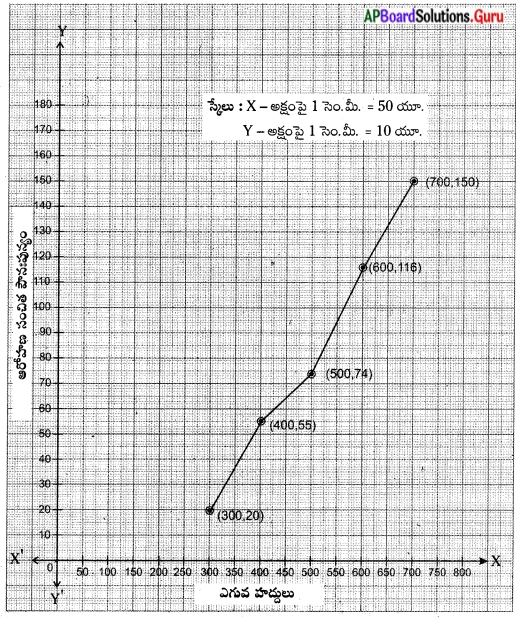
ప్రశ్న 16.
క్రింద ఇవ్వబడిన పట్టికలో 25 కుటుంబాలు ఆహారానికి వెచ్చించే దినసరి ఖర్చులు ఇవ్వబడినవి. ఆ దత్తాంశానికి బాహుళకంను కనుగొనండి.

సాధన.

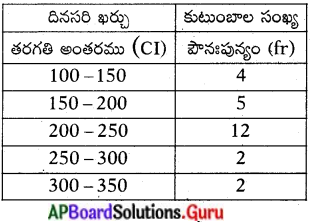
భాహుళకము = l + [latex]\left(\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right)[/latex] × h

‘l’ = బాహుళక తరగతి దిగువ హద్దు = 200
‘f₁‘ – బాహుళక తరగతి పౌనఃపున్యం = 12
‘f₀‘ – బాహుళక తరగతికి ముందున్న ఉన్న తరగతి పౌనఃపున్యం = 5
‘f₂‘ – బాహుళక తరగతికి తరువాత ఉన్న తరగతి పౌనఃపున్యం = 2
‘h’ – బాహుళక తరగతి పొడవు = 50 200-250 250-300
∴ బాహుళకము = 200 + ([latex]\frac{12-5}{24-5-2}[/latex]) × 50
= 200 + [latex]\frac{7 \times 50}{17}[/latex]
= 200 + [latex]\frac{350}{17}[/latex]
= 200 + 20.58
∴ బాహుళకము = 220.58.

ప్రశ్న 17.
ఒక పరీక్షలో 53 మంది విద్యార్థులకు వచ్చిన మార్కులు క్రింది పట్టికలో ఇవ్వబడినవి. ఆ దత్తాంశానికి “ఆరోహణ సంచిత పౌనఃపున్య వక్రం”ను గీయండి.

సాధన.

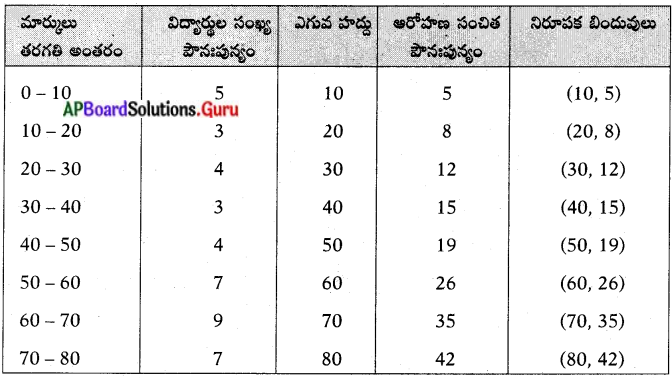
ఆరోహణ సంచిత పౌనఃపున్య ఓజీవ్ వక్రం గీయుట కొరకు X-అక్షంపై తరగతి ఎగువ హద్దును, Y-అక్షంపై ఆరోహణ సంచిత పౌనఃపున్యమును తీసుకొనవలెను.

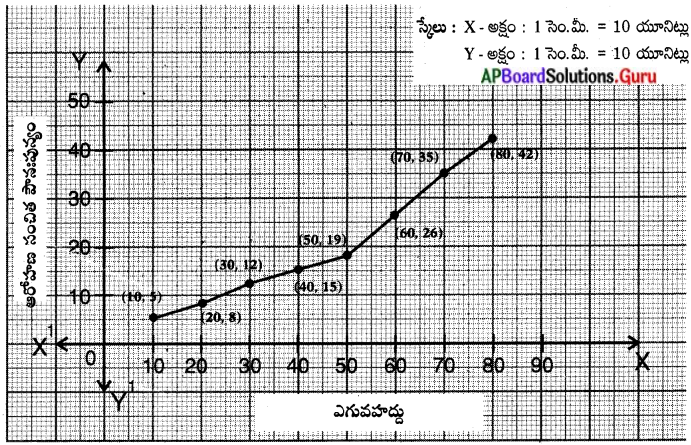
ప్రశ్న 18.
ఒక వాణిజ్య సంస్థ యందు కార్మికుల రోజువారీ వేతనములు క్రింది పౌనఃపున్య విభాజనము నందు ఇవ్వబడినవి. ఈ విభాజనము యొక్క సగటు ₹ 220. అయితే ఇందు లోపించిన పౌనఃపున్యం f ను కనుగొనుము.

సాధన.

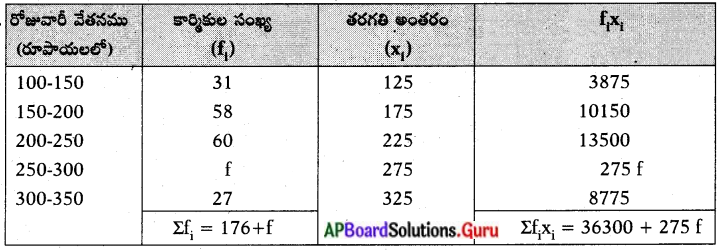
ఇచ్చినది, x_i = 220
[latex]\overline{\mathrm{X}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{X}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}[/latex]
⇒ 220 = [latex]\frac{36300+275 \mathrm{f}}{176+\mathrm{f}}[/latex]
⇒ 220(176 + f) = 36300 + 275f
⇒ 38720 + 220 f = 36300 + 275 f
⇒ 220 f – 275 f = 36300 – 38720
⇒ – 55 f = – 2420
⇒ f = [latex]\frac{2420}{55}[/latex] = 44.

These AP 10th Class Maths Chapter Wise Important Questions 13th Lesson సంభావ్యత will help students prepare well for the exams

AP Board 10th Class Maths 13th Lesson Important Questions and Answers సంభావ్యత

ప్రశ్న 1.
నీవు వ్రాయు ఒక పరీక్షలో 40 ఆబ్జెక్టివ్ ప్రశ్నలున్నాయి. ప్రతీ ప్రశ్నకూ 1 మార్కు. ఆ పరీక్షలో నీవు సాధించు మార్కులు “5 యొక్క గుణిజం” కావలెనంటే దాని సంభావ్యత ఎంత ?
సాధన.
మొత్తం ప్రశ్నల సంఖ్య = 40
మొత్తం పర్యవసానాల సంఖ్య = 40
40 వరకు 5 యొక్క గుణిజాల సంఖ్య = 8
అనుకూల పర్యవసానాల సంఖ్య = 8
5 యొక్క గుణిజం అగుటకు సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం సాధ్యమయ్యే పర్యవసానముల సంఖ్య
= [latex]\frac{8}{40}=\frac{1}{5}[/latex].

ప్రశ్న 2.
100 పేజీలు గల ఒక పుస్తకమునందు యాదృచ్ఛికంగా తెరువబడిన పేజీ సంఖ్య ఒక ‘ఖచ్చిత వర్గము అయ్యే సంభావ్యత కనుగొనుము.
సాధన.
ఒక పుస్తకం నందు గల మొత్తం పేజీల సంఖ్య = 100
ఈ పుస్తకం నుండి యాదృచ్ఛికంగా తెరవబడిన పేజీ సంఖ్య ఒక ఖచ్చిత వర్గ సంఖ్య అగుటకు గల పర్యవసానాలు = 1, 4, 9, 16, 25, 36, 49, 64, 81 మరియు 100 నెంబర్లు గల పేజీలు.
∴ అనుకూల పర్యవసానాల సంఖ్య = 10
మొత్తం పర్యవసానాల సంఖ్య = 100
∴ పై ఘటన యొక్క సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{10}{100}[/latex] = 0.1

ప్రశ్న 3.
P(E) = 0.546, అయిన ‘E కాదు! యొక్క సంభావ్యత ఎంత ?
సాధన.
P(E) = 0.546
P(E) = 1 – P(E)
“E కాదు” సంభావ్యత = 1 – 0.546 = 0.454.

ప్రశ్న 4.
ఒక పెట్టెలో 3 నీలం రంగు మరియు 4 ఎర్రబంతులు కలవు. యాదృచ్ఛికంగా పెట్టె నుండి తీయబడిన బంతి ఎరుపు బంతి అగుటకు సంభావ్యత ఎంత ?
సాధన.
మొత్తం బంతుల సంఖ్య = 3 + 4 = 7.
మొత్తం పర్యవసానాల సంఖ్య = 7
ఎర్రబంతి అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 4
తీసిన బంతి ఎర్రబంతి అగుటకు సంభావ్యత = [latex]\frac{4}{7}[/latex]

ప్రశ్న 5.
ఒక తరగతిలో 60 మంది విద్యార్థులు కలరు. వారిలో 32 మంది టీ త్రాగుదురు. టీ త్రాగని వారి సంభావ్యత ఎంత ?
సాధన.
మొత్తం పర్యవసానాల సంఖ్య = 60
టీ త్రాగని వారి సంఖ్య (అనుకూల పర్యవసానాల సంఖ్య) = 60 – 32 = 28
టీ త్రాగని వారి సంభావ్యత = టీ త్రాగకుండుటకు అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{28}{60}=\frac{7}{15}[/latex]

ప్రశ్న 6.
‘సమసంభవ ఘటనలు’ అనగానేమి ? ఒక ఉదాహరణ ఇవ్వండి.
సాధన.
సమసంభవ ఘటనలు :
ఒక ప్రయోగంలో రెండు లేక అంతకన్నా ఎక్కువ ఘటనలు సంభవించడానికి సమాన అవకాశములు ఉంటే వాటిని సమసంభవ ఘటనలు అంటారు.
ఉదా : ఒక నాణేన్ని ఎగురవేసినపుడు బొమ్మ లేదా బొరుసు పడే సంభావ్యత.

ప్రశ్న 7.
ఒక సంచిలో 5. ఎరుపు, 8 తెలుపు బంతులు కలవు. ఆ సంచి నుండి యాదృచ్ఛికంగా ఒక బంతిని తీస్తే అది i) తెలుపు బంతి అయ్యే ii) తెలుపు బంతి కాకుండా సంభావ్యత ఎంత ?
సాధన.
సంచిలోని మొత్తం బంతుల సంఖ్య = 5 + 8 = 13
5 ఎరుపు + 8 తెలుపు = 13
తెలుపు బంతి అగుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{5}{13}[/latex]
P(E) = [latex]\frac{8}{13}[/latex]
తెలుపు బంతి కాకుండుటకు సంభావ్యత = P([latex]\overline{\mathrm{E}}[/latex]) = ?
P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = 1
⇒ P([latex]\overline{\mathrm{E}}[/latex]) = 1 – P(E)
= 1 – [latex]\frac{8}{13}[/latex] = [latex]\frac{5}{13}[/latex]

ప్రశ్న 8.
ఒక పెట్టెలో 1 నుండి 5 వరకు అంకెలు వ్రాయబడిన 5 కార్డులున్నాయి. వాటి నుండి ఏవైనా 2 కార్డులు తీసినచో, ఏర్పడే అనుకూల పర్యవసానాలు అన్నీ వ్రాసి, ఆ 2 కార్డులపై సరిసంఖ్యలుండే సంభావ్యత కనుగొనండి.
సాధన.
రెండు కార్డులను బాక్సు నుండి తీసుకొన్నప్పుడు వీలైన
అన్ని పర్యవసానాలు
(1, 2), (1, 3), (1, 4), (1, 5) (2, 3), (2, 4), (2, 5) (3,4), (3, 5), (4, 5)
∴ మొత్తం పర్యవసానాల సంఖ్య = 10
రెండు కార్డులపై సరి సంఖ్యలు అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 1, (అది (2, 4))
రెండు కార్డులపైనా సరి సంఖ్యలు వచ్చే సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య

ప్రశ్న 9.
ఒక పాచికను ఒక్కసారి దొర్లించినపుడు ఈ క్రింది ఘటనల సంభావ్యతలను కనుక్కోండి.
(i) సరి సంఖ్య
(ii) బేసి ప్రధాన సంఖ్య
సాధన.
ఒకసారి పాచికను దొర్లించిన మొత్తం పర్యవసానాల సంఖ్య = 6
(i) సరిసంఖ్య వచ్చుటకు అనుకూల పర్యవసానాల సంఖ్య = 3
సరిసంఖ్య వచ్చుటకు సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{3}{6}=\frac{1}{2}[/latex]

(ii) బేని ప్రధాన సంఖ్య వచ్చుటకు అనుకూల పర్యవసానాల సంఖ్య = 2
బేసి ప్రధానసంఖ్య వచ్చుటకు సంభావ్యత = [latex]\frac{2}{6}=\frac{1}{3}[/latex].

ప్రశ్న 10.
పాచికను ఉపయోగించి సంభావ్యతను కనుగొను రెండు సమస్యలను వ్రాయుము.
సాధన.
పాచికను ఉపయోగించి సంభావ్యత కనుగొనుటకు రెండు సమస్యలు :
1) పాచికను ఒకసారి దొర్లించినపుడు దానిపైన సరిసంఖ్య వచ్చుటకు సంభావ్యత ఎంత ?
2) పాచికను ఒకసారి దొర్లించినపుడు దానిపైన బేసి సంఖ్య వచ్చుటకు సంభావ్యత ఎంత ?

ప్రశ్న 11.
సంచిలో ఒకే పరిమాణం కలిగిన 5.ఎరుపు, 5 ఆకుపచ్చ మరియు 5 తెలుపు బంతులు కలవు. అందులో నుండి ఒక బంతిని యాదృచ్ఛికంగా తీయగా ఆ బంతి ఆకుపచ్చ, ఎరుపు లేదా తెలుపు రంగు వచ్చే సంభావ్యతలు సమసంభవాలా? కాదా? సమర్థించండి.
సాధన.
ఎరుపు బంతుల సంఖ్య = 5 = n(R)
ఆకుపచ్చ బంతుల సంఖ్య = 5 = n(G)
తెలుపు బంతుల సంఖ్య = 5 = n(W)
మొత్తం బంతులు = 15 = T(B)
ఎరుపు బంతులను తీయగలిగిన సంభావ్యత = P(R)
= ఎరుపు బంతుల సంఖ్య / మొతం బంతులు
= [latex]\frac{5}{15}=\frac{1}{3}[/latex]
ఆకుపచ్చ బంతులను తీయగలిగిన సంభావ్యత = [latex]\frac{5}{15}=\frac{1}{3}[/latex]
తెలుపు బంతులను తీయగలిగిన సంభావ్యత = [latex]\frac{5}{15}=\frac{1}{3}[/latex]
సంభావ్యతలన్నీ సమానములు.
కావున అన్ని పర్యవసానములు సమసంభవాలు.

ప్రశ్న 12.
ఒక పేక ముక్కల కట్ట నుండి ఏస్, రాజు మరియు 10 సంఖ్య గల 3 కళావరు ముక్కలను బయటకు తీసి, మిగిలిన వాటిని బాగా కలిపి, వాటి నుండి ఒక పేక ముక్కను తీసినచో అది
(i) కళావరు అగుటకు,
(ii) ఏస్ అగుటకు,
(iii) డైమండ్ రాజు అగుటకు,
(iv) కళావరు 5 అగుటకు సంభావ్యత కనుగొనండి.
సాధన.
మొత్తం పర్యవసానాల సంఖ్య 52 – 3 = 49
(i) తీసిన ముక్క కళావరు అగుటకు సంభావ్యత = కళావరు అగుటకు అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానముల సంఖ్య
= [latex]\frac{10}{49}[/latex]

(ii) తీసిన ముక్క ఆసు అగుటకు సంభావ్యత = [latex]\frac{3}{49}[/latex]
(iii) తీసిన ముక్క డైమండ్ రాజు అగుటకు సంభావ్యత = [latex]\frac{1}{49}[/latex]
(iv)తీసిన ముక్క కళావరు 5 అగుటకు సంభావ్యత = [latex]\frac{1}{49}[/latex]

ప్రశ్న 13.
ఒక సంచిలో 1 నుండి 20 వరకు వ్రాయబడి ఉన్న 20 ఫలకాలు ఉన్నాయి. వాటి నుండి యాదృచ్ఛికంగా ఒక ఫలకాన్ని ఎన్నుకొంటే దానిపై క్రింది సంఖ్యలు ఉండుటకు సంభావ్యత ఎంత ?
(i) సరి సంఖ్య
(ii) ప్రధాన సంఖ్య
(iii) 5 యొక్క గుణిజము
(iv) రెండంకెల బేసి సంఖ్య
సాధన.
మొత్తం పర్యవసానాల సంఖ్య = 20
(i) తీసిన ఫలకము పైన ఉండు సంఖ్య సరిసంఖ్య అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 10
సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{10}{20}=\frac{1}{2}[/latex]

(ii) తీసిన ఫలకముపైన ఉండు సంఖ్య ప్రధాన సంఖ్య అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 8.
సంభావ్యత = [latex]\frac{8}{20}=\frac{2}{5}[/latex]

(iii) తీసిన ఫలకము పైన ఉండు సంఖ్య 5 యొక్క గుణిజము అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 4
∴ సంభావ్యత = [latex]\frac{4}{20}=\frac{1}{5}[/latex]

(iv) తీసిన ఫలకముపైన ఉండు సంఖ్య రెండంకెల బేసి సంఖ్య అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 5
∴ సంభావ్యత = [latex]\frac{5}{20}=\frac{1}{4}[/latex]

ప్రశ్న 14.
రెండు పాచికలను ఒకేసారి దొర్లించడం జరిగింది. రెండు పాచికలపై కనిపించే సంఖ్యల మొత్తం
(a) 10,
(b) 12 లేక అంతకన్నా తక్కువ,
(c) ప్రధాన సంఖ్య,
(d) ‘3’ యొక్క గుణిజం అగుటకు సంభావ్యతలను కనుగొనుము.
సాధన.
రెండు పాచికలను ఒకేసారి దొర్లించిన సాధ్యపడు మొత్తం పర్యవసానాలు S =

మొత్తం,సాధ్యపడు పర్యవసానాల సంఖ్య = 6 × 6 = 36
రెండు సంఖ్యల మొత్తం 10 అయ్యే ఘటనకు అనుకూల
పర్యవసానాలు = (4, 6), (5, 5), (6, 4) .

(a) రెండు సంఖ్యల మొత్తం 10 అయ్యే ఘటనకు అనుకూల పర్యవసానాల సంఖ్య = 3

P(E) = E కు అనుకూల పర్యవసానాల సంఖ్య / మొత్తం సాధ్యపడు పర్యవసానాల సంఖ్య
P(మొత్తం 10) = [latex]\frac{3}{36}=\frac{1}{12}[/latex]

(b) రెండు సంఖ్యల మొత్తము 12 లేక అంతకన్నా తక్కువ అయ్యే ఘటనకు అనుకూల పర్యవసానాల సంఖ్య = 36
P(మొత్తము ≤ 12) = [latex]\frac{36}{36}[/latex] = 1

(c) రెండు సంఖ్యల మొత్తము ప్రధాన సంఖ్య అయ్యే ఘటనకు అనుకూల పర్యవసానాలు = (1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)
రెండు సంఖ్యల మొత్తము ప్రధాన సంఖ్య అయ్యే ఘటనకు అనుకూల పర్యవసానాల సంఖ్య = 15
P(రెండు సంఖ్యల మొత్తం ప్రధాన సంఖ్య) = [latex]\frac{15}{36}=\frac{5}{12}[/latex]

(d) రెండు సంఖ్యల మొత్తము 3 యొక్క గుణిజము అయ్యే ఘటనకు అనుకూల పర్యవసానాలు = (1, 2), (1, 5), (2, 1), (2, 4), (3, 3), (3,6), (4, 2), (4, 5), (5, 1), (5, 4), (6, 3), (6, 6)
రెండు సంఖ్యల మొత్తము 3 యొక్క గుణిజము అయ్యే ఘటనకు అనుకూల పర్యవసానాల సంఖ్య: :
= 12
P(రెండు సంఖ్యల మొత్తము 3 యొక్క గుణిజము) = [latex]\frac{12}{36}=\frac{1}{3}[/latex]

ప్రశ్న 15.
బాగుగా కలుపబడిన పేకముక్కల’ (52) కట్ట నుండి యాదృచ్ఛికంగా ఒక కార్డును తీస్తే అది క్రింది కార్డు అగుటకు సంభావ్యతను లెక్కించండి.
(i) ఎరుపు రాజు
(ii) నలుపు జాకీ
(iii) నలుపు ముఖ కార్డు
(iv) డైమండ్ గుర్తు గల రాణి
సాధన.
పేకముక్కల సంఖ్య = 52
మొత్తం పర్యవసానాల సంఖ్య = 52
బాగుగా కలుపబడిన పేకముక్కల కట్ట నుండి యాదృచ్ఛికంగా ఒక కార్డును తీస్తే అది
(i) ఎరుపు రాజు కార్డు అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 2
సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= [latex]\frac{2}{52}=\frac{1}{26}[/latex]

(ii) నలుపు “జాకీ – కార్డు అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 2
సంభావ్యత = [latex]\frac{2}{52}=\frac{1}{26}[/latex]

(iii) నలుపు ముఖ కార్డు అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 6.
సంభావ్యత = [latex]\frac{6}{52}=\frac{3}{26}[/latex]

(iv) డైమండ్ ‘గుర్తు గల రాణి కార్డు అగుటకు అనుకూల పర్యవసానాల సంఖ్య = 1
∴ సంభావ్యత = [latex]\frac{1}{52}[/latex]

ప్రశ్న 16.
0, 1, 2, 3 మరియు 4 అనే అంకెలతో ఏర్పడే రెండంకెల సంఖ్యలలో (ఒక అంకె ఒకసారి మాత్రమే ఉపయోగించగా)
(i) 42 కంటే పెద్ద సంఖ్య
(ii) 4 యొక్క గుణిజం అగుటకు గల సంభావ్యత కనుగొనుము.
సాధన.
ఒక అంకెను ఒకేసారి ఉపయోగించి 0, 1, 2, 3 మరియు 4 అనే అంకెలతో ఏర్పడే రెండంకెల సంఖ్యలు. (10, 12, 13, 14, 20, 21, 23, 24, 30, 31, – 32, 34, 40, 41, 42, 43)
∴ అనుకూల పర్యవసానాలు = (10, 12, 13, 14, 20, 21, 23, 24, 30, 31, 32, 34, 40, 41, 42, 43)
∴ n(s) = 16
∴ అనుకూలపర్యవసానాల సంఖ్య = 16

(i) 42 కంటే పెద్ద సంఖ్యలు ఏర్పడే సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాలు
ఇక్కడ, అనుకూల పర్యవసానాల సంఖ్య = 1 (43 మాత్రమే)
∴ సంభావ్యత = 1

(ii) అనుకూల పర్యవసానాలలో 4 యొక్క గుణిజాలు = 12, 20, 24, 32, 40
∴ 4 యొక్క గుణిజాల సంఖ్య = 5
‘4’ యొక్క గుణిజాలు ఏర్పడే సంభావ్యత = [latex]\frac{5}{16}[/latex]

These AP 10th Class Maths Chapter Wise Important Questions 12th Lesson త్రికోణమితి అనువర్తనాలు will help students prepare well for the exams

AP Board 10th Class Maths 12th Lesson Important Questions and Answers త్రికోణమితి అనువర్తనాలు

ప్రశ్న 1.
ఒక బాలుడు విద్యుత్ స్తంభం అడుగు భాగం నుండి 10 మీ. దూరంలో ఉన్న బిందువు నుండి విద్యుత్ 2. స్తంభం పై భాగాన్ని 30° ఊర్ధ్వకోణంతో పరిశీలించాడు. ఈ సందర్భానికి సరిపడు పటాన్ని గీయండి.
సాధన.

AB = విద్యుత్ స్తంభం ఎత్తు
AC = విద్యుత్ స్తంభం
అడుగు భాగం నుండి పరిశీలకునికి గల దూరం = 10 మీ.
ఊర్థ్వకోణం = 30°.

ప్రశ్న 2.
క్రింది సన్నివేశంలో గాలిపటం ఎత్తు కనుగొనుటకు తగిన పటాన్ని గీయండి. “ఒక వ్యక్తి ‘I’ పొడవు గల దారంతో కూడిన గాలిపటాన్ని ‘d ఊర్ధ్వకోణంతో ఎగుర వేయుచున్నాడు”.
సాధన.

‘B’ వద్ద గాలిపటం ఉంది.
BC = దారం పొడవు = ‘l’

ప్రశ్న 3.
ఒక టవర్ ఎత్తు 100√3 మీటర్లు. దాని పాదం నుండి 100 మీటర్ల దూరంలో గల ఒక బిందువు నుండి ఆ టవర్ పై భాగాన్ని చూడాలంటే ఎంత ఊర్థ్వ కోణంతో చూడాలో కనుగొనండి.
సాధన.

టవర్ ఎత్తు AB = 100√3 మీ.
టవర్ అడుగు భాగం నుండి పరిశీలకునికి గల దూరం BC = 100 మీ.
∆ABC లో tan θ = [latex]\frac{100 \sqrt{3}}{100}[/latex] = √3
= tan 60°
⇒ θ = 60°.

ప్రశ్న 4.
రెహమాన్ ఒక గుడి గోపురం అడుగు భాగం నుండి 24 మీ. దూరంలో గల పరిశీలక స్థానం నుండి గోపుర శిఖరాన్ని 30° ఊర్ద్వకోణంతో పరిశీలించిన ఆ గోపురం ఎతును కనుక్కోండి.
సాధన.

పరిశీలకునికి, గుడి గోపురం అడుగుభాగానికి మధ్య గల దూరం = 24 మీ.
గుడి గోపురం ఎత్తు = h మీ. .
θ = 30°
∆ABC నుండి
tan 30° = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}[/latex]
[latex]\frac{1}{\sqrt{3}}=\frac{h}{24}[/latex]
⇒ h = [latex]\frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}[/latex] = 8√3 మీ…
గుడి గోపురం ఎత్తు = 8√3.మీ.

ప్రశ్న 5.
1.8 మీ. ఎత్తు కల్గిన ‘ఒక పరిశీలకుడు 13.2 మీ. దూరంలో గల చెట్టు పైభాగాన్ని తన కంటి నుండి 45° ఊర్ధ్వకోణంతో పరిశీలిస్తున్నాడు. అయిన ఆ తాటిచెట్టు ఎత్తు ఎంత ?
సాధన.
పరిశీలకుని ఎత్తు = 1.8 మీ. = AB
చెట్టు నుండి దూరము = 13.2 మీ. = AE = BD
ఊర్థ్వకోణము = ∠CBD = 45°

∆ BCD లో tan 45° = [latex]\frac{C D}{B D}[/latex]
⇒ 1 = [latex]\frac{\mathrm{CD}}{13.2}[/latex]
CD = 13.2 మీ.
∴ తాటిచెట్టు ఎత్తు = CE
= CD + DE
= 13.2 మీ. + 1.8 = 15 మీ.

ప్రశ్న 6.
7 మీ. పొడవుగల ఒక జెండా స్థంభము 8మీ. పొడవు గల నీడను ఏర్పరుచును. అదే సమయములో దగ్గరలో గల ఒక భవనము 32 మీ. పొడవు గల నీడను ఏర్పరచిన ఆ భవనము ఎత్తు ఎంత ?
సాధన.

∆ABC ~ ∆DEF;
[latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}[/latex]
[latex]\frac{7}{\mathrm{DE}}=\frac{8}{32}[/latex]
∴ DE = 28 మీ.

ప్రశ్న 7.
6 మీ. మరియు 11 మీ. పొడవు గల స్తంభాలు ఒక చదునైన నేలపై కలవు. నేలపై ఆ రెండు స్తంభాల అడుగు భాగాల మధ్య దూరము 12 మీ. అయిన ఆ రెండు స్తంభాల పైభాగముల మధ్య దూరం ఎంత ?
సాధన.
దత్తాంశం ప్రకారం,
మొదటి స్తంభము పొడవు = AB = 6 మీ.
రెండవ స్తంభము పొడవు = CD = 11 మీ.

రెండు స్తంభాల అడుగు భాగాల మధ్య దూరము = AC = 12 మీ.
రెండు స్తంభాల పైభాగముల మధ్యదూరము = BD
పటం ప్రకారం,
BE = AC = 12 మీ.;
AB = EC = 6 మీ.
∴ DE = DC – EC
= 11 – 6 = 5 మీ.
BD² = DE² + BE²
= 5² + 12²
= 25 + 144 = 169
∴ BD = √169 = 13 మీ.

ప్రశ్న 8.
900 మీ. ఎత్తులో ఎగురుతున్న విమానం నుండి ఒక పరిశీలకుడు అతనికి ముందు వైపు అదే రేఖలో రెండు నావలను 60° మరియు 30° నిమ్నకోణాలతో గమనించిన ఆ రెండు నావల మధ్య దూరమెంత ?
సాధన.

∆ABC లో tan 60 = [latex]\frac{900}{x}[/latex]
√3 = [latex]\frac{900}{x}[/latex]
⇒ x = [latex]\frac{900}{\sqrt{3}}[/latex] = 300√3
∆ABD లో tan 30 = [latex]\frac{900}{x+d}[/latex]
[latex]\frac{1}{\sqrt{3}}=\frac{900}{300 \sqrt{3}+d}[/latex]
d = 600√3 మీ.

ప్రశ్న 9.
భూమితో 30°ల ఊర్ధ్వ కోణము చేస్తూ 24 మీటర్ల పొడవున్న ఒక దృఢమైన లోహపు తీగ ఆధారంగా ఒక విద్యుత్ స్థంభము నిలబెట్టబడి ఉంది. తీగ పొడవు చాలా ఎక్కువ ఉన్న కారణంగా తీగలో కొంత భాగము కత్తిరించి, మిగిలిన దానిని భూమితో 60° కోణము చేస్తూ అమర్చబడినది. అయిన కత్తిరించిన తీగ పొడవు ఎంత?
సాధన.
కత్తిరించకముందు లోహపు తీగ పొడవు (AD) = 24 మీ.
కత్తిరించిన తదుపరి లోహపు తీగ పొడవు (AC) = x మీ.
కరెంటు స్తంభము ఎత్తు = AB
ఊర్వకోణము ∠BDA = 30°; ∠BCA = 60°
లంబకోణ త్రిభుజము ABD నుండి

sin 30° = [latex]\frac{\mathrm{AB}}{\mathrm{AD}}[/latex]
[latex]\frac{1}{2}=\frac{\mathrm{AB}}{24}[/latex]
2AB = 24
AB = 12 మీ.
లంబకోణ త్రిభుజము ABC నుండి
sin 60° = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}[/latex]
⇒ [latex]\frac{\sqrt{3}}{2}=\frac{12}{\mathrm{AC}}[/latex]
√3 AC = 24
⇒AC = [latex]\frac{24}{\sqrt{3}}[/latex] = 8√3 మీ.
= 8 × 1.732 = 13.856 మీ.
కత్తిరించిన తీగ పొడవు = 24 – 13.856 = 10.144 మీ.

ప్రశ్న 10.
ఒక వ్యక్తి నిలువాటి టవర్ పై భాగం నుండి సమవేగంతో తనవైపు వస్తున్న కారును 30° నిమ్నకోణంతో పరిశీలిస్తున్నాడు. 12 సెకండ్ల తర్వాత నిమ్నకోణం 30° నుండి 60° కు మారిన ఆ స్థానం నుండి పరిశీలక స్థానం చేరుటకు ఎంతకాలం పట్టును ?
సాధన.
పటం నుండి,
సెకండ్లలో కారు ప్రయాణించిన దూరం = AB = x మీటర్లు
టవర్ ఎత్తు CD = h మీటర్లు

కారు ప్రయాణించాల్సిన మిగిలిన దూరం BC = d మీటర్లు
AC = AB + BC = (x + d) మీటర్లు
∠PDA = ∠DAC = 30°
∠PDB = ∠DBC = 60°
∆BCD నుండి, tan 60° = [latex]\frac{C D}{B C}[/latex]
√3 = [latex]\frac{h}{d}[/latex]
⇒ h = √3d ………… (1)
∆ACD నుండి,
tan 30° = [latex]\frac{C D}{A C}[/latex]
[latex]\frac{1}{\sqrt{3}}=\frac{h}{(x+d)}[/latex]
⇒ h = [latex]\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}[/latex] …………… (2)
(1) మరియు (2)ల నుండి,
[latex]\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}[/latex] = √3d
⇒ x + d = 3d
⇒ x = 2d
⇒ d = A
‘x’ మీటర్ల దూరం ప్రయాణించడానికి పట్టు కాలం = 12 సెకండ్లు
‘d’ = [latex]\frac{x}{2}[/latex] మీటర్ల దూరం ప్రయాణించడానికి పట్టు – కాలం = 6 సెకండ్లు.

ప్రశ్న 11.
60 మీటర్ల ఎత్తు గల ఒక గుడి పైభాగాన్ని దానికి ఇరువైపులా గల ఇద్దరు బాలురు 60° మరియు 30° ఊర్ధ్వకోణాలతో గమనిస్తే ఆ బాలురు మధ్య గల దూరాన్ని కనుగొనంది.
సాధన.
పటము నుండి దేవాలయం ఎత్తు BD = 60 మీటర్లు
మొదటి బాలుడు పరిశీలిస్తున్నపుడు ఊర్ధ్వకోణం ∠BAD = 60°
రెండవ బాలుడు పరిశీలిస్తున్నపుడు ఊర్థ్వకోణం ∠BCD = 30°
మొదటి బాలుడు నుండి గుడి దూరం AD = x,
రెండవ బాలుడు నుండి గుడి దూరం CD = d అనుకొనగా

∆BAD నుండి ∆BCD నుండి
tan 60° = [latex]\frac{\mathrm{BD}}{\mathrm{AD}}[/latex]
√3 = [latex]\frac{60}{x}[/latex]
x = [latex]\frac{60}{\sqrt{3}}[/latex] …………..(1)

tan 30° = [latex]\frac{\mathrm{BD}}{\mathrm{d}}[/latex]
[latex]\frac{1}{\sqrt{3}}=\frac{60}{d}[/latex]
d = 60√3 ……………. (2)
(1) మరియు (2) ల నుండి ఇద్దరు వ్యక్తుల మధ్య దూరం
= AD + AC = x + d
= [latex]\frac{60}{\sqrt{3}}[/latex] + 60√3
= [latex]\frac{60+180}{\sqrt{3}}[/latex]
= [latex]\frac{240}{\sqrt{3}}[/latex]
= 80√3 మీటర్లు.

These AP 10th Class Maths Chapter Wise Important Questions 11th Lesson త్రికోణమితి will help students prepare well for the exams

AP Board 10th Class Maths 11th Lesson Important Questions and Answers త్రికోణమితి

ప్రశ్న 1.
sin A = cos A అయిన A విలువను డిగ్రీలలో తెల్పండి.
సాధన.
sin A = cos A
⇒ sin A = sin (90 – A) (∵ A = 90 – A)
⇒ 2A = 90
⇒ A = [latex]\frac{90}{2}[/latex] = 45°

ప్రశ్న 2.
2 sin x = √3 అయినచో x విలువెంత?
సాధన.
2 sin x = √3
⇒ sin x = [latex]\frac{\sqrt{3}}{2}[/latex]
sin x = sin 60°
⇒ x = 60°.

ప్రశ్న 3.
గణించుము:
(i) cos 76° – sin 14°
(ii) [latex]\frac{\tan 73^{\circ}}{\cot 17^{\circ}}[/latex]
సాధన.
(i) cos 76° – sin 14° = cos (90 – 14) – sin 14
= sin 14° – sin 14° (∵ cos (90 – θ) = sin θ)
= 0
∴ cos 76° – sin 14° = 0 ………….(i)

(i) [latex]\frac{\tan 73^{\circ}}{\cot 17^{\circ}}[/latex] = [latex]\frac{\tan (90-17)}{\cot 17}=\frac{\cot 17^{\circ}}{\cot 17^{\circ}}[/latex]
= 1
∴ [latex]\frac{\tan 73^{\circ}}{\cot 17^{\circ}}[/latex] = 1

ప్రశ్న 4.
tan² 45° + cot² 30° విలువను కనుక్కోండి.
సాధన.
tan 45° + cot² 30°
= (1)² + (√3)²
= 1 + 3 = 4.

ప్రశ్న 5.
sin² 30° + cos² 60° విలువను కనుగొనుము.
సాధన.
sin 30° = [latex]\frac{1}{2}[/latex], cos 60° = [latex]\frac{1}{2}[/latex]
sin² 30° + cos² 60° = ([latex]\frac{1}{2}[/latex])² + ([latex]\frac{1}{2}[/latex])²
= [latex]\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}[/latex]
∴ sin² 30° + cos² 60° = [latex]\frac{1}{2}[/latex]

ప్రశ్న 6.
sin (A + B) = 1 మరియు cos B = [latex]\frac{1}{2}[/latex] ∠A, ∠Bలను కనుగొనుము. (0°< A + B ≤ 90°)
సాధన.
sin (A + B) = 1
sin (A + B) = sin 90°
A + B = 90°
cos B = [latex]\frac{1}{2}[/latex]
cos B = cos 60°
∴ ∠B = 60°
∴ ∠A = 90° – 60° = 30°.

ప్రశ్న 7.
cot² θ – [latex]\frac{1}{\sin ^{2} \theta}[/latex] ను సూక్ష్మీకరించండి.
సాధన.
[latex]\frac{\cos ^{2} \theta}{\sin ^{2} \theta}-\frac{1}{\sin ^{2} \theta}=\frac{\cos ^{2} \theta-1}{\sin ^{2} \theta}=\frac{\sin ^{2} \theta}{\sin ^{2} \theta}[/latex] = 1

ప్రశ్న 8.
‘θ’ ఏదేని అల్పకోణమైతే sin θ = [latex]\frac{5}{3}[/latex]; వ్యవస్థితమగునా? .. కారణం తెలపండి.
సాధన.
‘θ’ అల్పకోణము = 0° < θ < 90°
కనుక sin 0° = 0 మరియు sin 90° = 1
కనుక 0° < θ < 90°కు sin θ విలువ 0 మరియు 1ల మధ్య ఉంటుంది.
కనుక sin θ విలువ 1 కంటే ఎక్కువ ఉండదు.
∴ sin θ = [latex]\frac{5}{3}[/latex] వ్యవస్థతము కాదు.

ప్రశ్న 9.
sin x = [latex]\frac{3}{4}[/latex] అయితే cosec x విలువ కనుగొనుము.
సాధన.
sin x = [latex]\frac{3}{4}[/latex] అయితే
cosec x = [latex]\frac{1}{\sin x}=\frac{1}{\frac{3}{4}}=\frac{4}{3}[/latex]

ప్రశ్న 10.
sin 90°, cos 90°, tan 90°, cot 90°, sec 90° మరియు cosec 90° లలో ఏది( వి) నిర్వహించబడదు?
సాధన.
sin 90° = 1
cos 90° = 0
tan 90° = నిర్వహించబడదు
cot 90° = 0
sec 90° = నిర్వహించబడదు
cosec 90° = 1
∴ tan 90°, sec 90° లు నిర్వహించబడవు.

ప్రశ్న 11.
(sec² x – 1) (cot² x) ను సూక్ష్మ రూపంలో తెల్పండి.
సాధన.
(sec² x – 1) (cot² x) = (tan² x) (cot² x) [∵ sec²A – tan² A = 1]
= [latex]\frac{\sin ^{2} x}{\cos ^{2} x} \cdot \frac{\cos ^{2} x}{\sin ^{2} x}[/latex][tan A = [latex]\frac{\sin A}{\cos A}[/latex], cot A = [latex]\frac{\cos A}{\sin A}[/latex]]
= 1.

ప్రశ్న 12.
tan (A – B) = [latex]\frac{1}{\sqrt{3}}[/latex] మరియు sin A = [latex]\frac{\sqrt{3}}{2}[/latex] అయినచో ∠B మరియు cos B ల విలువలు కనుగొనండి (A, B < 90°)
సాధన.
tan (A – B) = [latex]\frac{1}{\sqrt{3}}[/latex]
∴ tan (A – B) = tan 30°
∴ A – B = 30°
sin A = [latex]\frac{\sqrt{3}}{2}[/latex]
sin A = sin 60°
∴ A = 60° ప్రతిక్షేపించిన
A – B = 30°
⇒ 60° – B = 30°
⇒ B = 30°
⇒ cos B = cos 30°
⇒ cos B = [latex]\frac{\sqrt{3}}{2}[/latex]

ప్రశ్న 13.
tan A = [latex]\frac{1}{\sqrt{3}}[/latex] మరియు tan B = √3 అయిన sin A . cos B + cos A . sin B విలువను కనుగొనుము (A, B < 90°)
సాధన.
tan A = [latex]\frac{1}{\sqrt{3}}[/latex] మరియు tan B = √3 (A, B < 90°)
∴ tan A = [latex]\frac{1}{\sqrt{3}}[/latex] = tan 30° (∵ A < 90°)
⇒ A = 30° మరియు tan B = √3 = tan 60° ⇒ B = 60°
(∵ AB < 90°)
⇒ A = 30°, B = 60° అయిన
sin A cos B + cos A sin B విలువ = sin 30° cos 60° + cos 30° sin 60°
∴ sin 30° cos 60° + cos 30° sin 60° = [latex]\frac{1}{2} \cdot \frac{1}{2}+\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}[/latex]
= [latex]\frac{1}{4}+\frac{3}{4}=\frac{4}{4}[/latex]
= 1

IInd method :
sin A cos B + cos A sin. B = sin (A + B) నందు
A = 30°, B = 60° ప్రతిక్షేపించిన
sin (A + B) = sin (30° + 60°)
= sin 90° = 1.

ప్రశ్న 14.
tan² A – sin² A = tan² A . sin² A అని చూపండి.
సాధన.
tan² A – sin² A = [latex]\frac{\sin ^{2} A}{\cos ^{2} A}[/latex] – sin² A
= sin² A ([latex]\frac{1}{\cos ^{2} A}[/latex] – 1)
= sin² A (sec² A – 1)
= sin² A. tan² A

ప్రశ్న 15.
cos A = [latex]\frac{7}{25}[/latex] అయిన sin A మరియు cosec A లను కనుగొనండి. నీవేమి గమనించితివి ?
సాధన.

∆ABC లంబకోణ త్రిభుజరీలో
cos A = [latex]\frac{7}{25}=\frac{\mathrm{AB}}{\mathrm{AC}}[/latex]
x² + 7² = 25²
x² = 25² – 7² = 576
x = 24
sin A = [latex]\frac{24}{25}[/latex] cosec A = [latex]\frac{25}{24}[/latex]
cosec A = [latex]\frac{1}{\sin A}[/latex] అని పరిశీలించితిని.

ప్రశ్న 16.
tan 2A = cot (A – 18°), 2A ఒక అల్పకోణము అయితే A యొక్క విలువను కనుగొనుము.
సాధన.
tan 2A = cot(A – 18°)
= cot[90 – (90 – (A – 18°)]]
tan 2A = tan [90 – (A – 18°)]
2A = 90 – (A – 18°)
= 90 – A + 18°
⇒ 3A = 108°
∴ A = 36°

ప్రశ్న 17.
4 tan θ = 3 అయిన sec e మరియు cosec 2ల విలువలు కనుగొనుము.
సాధన.
4 tan θ = 3
⇒ tan θ = [latex]\frac{3}{4}[/latex]

AC = [latex]\sqrt{\mathrm{BC}^{2}+\mathrm{AB}^{2}}[/latex]
= [latex]\sqrt{4^{2}+3^{2}}[/latex] = 5
sec θ = [latex]\frac{5}{4}[/latex]; cosec θ = [latex]\frac{5}{3}[/latex].

ప్రశ్న 18.
tan 2A = cot (A – 27), 2A అల్పకోణమైన A విలువ కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, 2A అల్పకోణము
tan 2A = cot (A – 27)
⇒ 2A + A – 27 = 90
⇒ 2A + A = 90 + 27 (∵ tan (90 – θ) = cot θ)
⇒ 3A = 117
⇒ A = [latex]\frac{117}{3}[/latex] = 39
∴ A = 39°

ప్రశ్న 19.
[latex]\sqrt{\frac{1+\sin A}{1-\sin A}}[/latex] = sec A + tan A అని చూపండి.
సాధన.
[latex]\sqrt{\frac{1+\sin A}{1-\sin A}}[/latex]
(లవ, హారాలను [latex]\sqrt{1+\sin A}[/latex] తో గుణించిన)

ప్రశ్న 20.
(sin x – cos x)² + (sin x + cos x)² విలువ కనుగొనండి.
సాధన.
(sin x – cos x)² + (sin x + cos x)² = sin² x + cos² x – 2 sin x cos x + sin² x + cos² x + 2 sin x cos x
= 2(sin² x + cos² x) = 2(1) = 2

ప్రశ్న 21.
cos A = [latex]\frac{12}{13}[/latex] అయితే sin A మరియు tan A విలువను కనుగొనండి.
సాధన.

AC² = AB² + BC²
13² = 12² + x²
169 = 144 + x²
x² = 25
⇒ x = 5
sin A = [latex]\frac{5}{13}[/latex]
tan A = [latex]\frac{\sin A}{\cos A}=\frac{\frac{5}{13}}{\frac{12}{13}}=\frac{5}{13} \times \frac{13}{12}=\frac{5}{12}[/latex]
∴ sin A = [latex]\frac{5}{13}[/latex], tan A = [latex]\frac{5}{12}[/latex].

ప్రశ్న 22.
4 sin² θ – 1 = 0 అయిన (θ < 90) θ విలువ కనుగొని cos² θ + tan² θ విలువను కనుగొనండి
సాధన.
4 sin² θ – 1 = 0
⇒ 4 sin² θ = 1
sin² θ = [latex]\frac{1}{4}[/latex]
⇒ sin θ = ± [latex]\sqrt{\frac{1}{4}}[/latex]
= ± [latex]\frac{1}{2}[/latex]
θ < 90°. అని ఇవ్వబడింది
కాబట్టి sin θ = [latex]\frac{1}{2}[/latex]
∴ θ = 30°
cos θ = cos 30° = [latex]\frac{\sqrt{3}}{2}[/latex]
tan θ = tan 30° = [latex]\frac{1}{\sqrt{3}}[/latex]
cos² θ + tan² θ = [latex]\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}[/latex]
= [latex]\frac{3}{4}+\frac{1}{3}=\frac{9+4}{12}=\frac{13}{12}[/latex]

ప్రశ్న 23.
(sin θ – cosec θ)² + (cos θ – sec θ)² = cot θ + tan² θ – 1 అని నిరూపించండి.
సాధన.
(sin θ – cosec θ)² + (cos θ – sec θ)² = sin² θ + cosec² θ – 2 sin θ . cosec θ + cos² θ + sec² θ – 2 cos θ · sec θ
= (sin² θ + cos² θ) + cosec² θ + sec² θ – 2 – 2
= 1 + (1 + cot² θ) + (1 + tan² θ) – 2 – 2
= cot² θ + tan² θ + 3 – 4
= cot² θ + tan ² θ – 1.

ప్రశ్న 24.
cosec θ + cot θ = p అయితే [latex]\frac{p^{2}+1}{p^{2}-1}[/latex] = sec θ అని చూపండి.
సాధన.
cosec θ + cot θ = p.
∴ cosec θ – cot θ = [latex]\frac{1}{p}[/latex]
cosec θ + cot θ = p
2 cosec θ = p + [latex]\frac{1}{p}[/latex]
cosec θ – cot θ = [latex]\frac{1}{p}[/latex]
2 cot θ = p – [latex]\frac{1}{p}[/latex]
= [latex]\frac{p^{2}-1}{p}[/latex]
[latex]\frac{\frac{p^{2}+1}{p}}{\frac{p^{2}-1}{p}}=\frac{2 \cosec \theta}{2 \cot \theta}[/latex]

[latex]\frac{\mathrm{p}^{2}+1}{\mathrm{p}^{2}-1}=\frac{\frac{1}{\sin \theta}}{\frac{\cos \theta}{\sin \theta}}=\frac{1}{\cos \theta}[/latex] = sec θ.

ప్రశ్న 25.
sec θ + tan θ = p. అయిన sin θ = [latex]\frac{p^{2}-1}{p^{2}+1}[/latex] అని నిరూపించండి.
సాధన.
sec θ + tan θ = p
sec² θ – tan² θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
p. (sec θ – tan θ) = 1

ప్రశ్న 26.
cot θ = [latex]\frac{7}{8}[/latex] అయిన
(i) [latex]\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}[/latex]
(ii) [latex]\frac{1+\cos \theta}{\sin \theta}[/latex] విలువలు కనుగొన౦డి.
సాధన.
(i) [latex]\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}[/latex] = [latex]\frac{1-\sin ^{2} \theta}{1-\cos ^{2} \theta}=\frac{\cos ^{2} \theta}{\sin ^{2} \theta}[/latex]
= cot² θ.
= [latex]\left(\frac{7}{8}\right)^{2}=\frac{49}{64}[/latex] → (1)
(∵ sin² θ + cos² θ = 1)

(ii) [latex]\frac{1+\cos \theta}{\sin \theta}[/latex] = [latex]\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}[/latex]
= cosec θ + cot θ
cot θ = [latex]\frac{7}{8}[/latex] కావున, (1 + cot² θ) = cosec² θ
⇒ 1 + ([latex]\frac{7}{8}[/latex])² = cosec² θ
⇒ 1 + [latex]\frac{49}{64}[/latex] = [latex]\frac{64+49}{64}=\frac{113}{64}[/latex]
∴ cosec θ = [latex]\sqrt{\frac{113}{64}}[/latex]
∴ [latex]\frac{1+\cos \theta}{\sin \theta}[/latex] = cosec θ + cot θ
= [latex]\frac{\sqrt{113}}{8}+\frac{7}{8}=\frac{7+\sqrt{113}}{8}[/latex].

ప్రశ్న 27.
sec² θ + cosec² θ = sec² θ . cosec² θ .
సాధన.
sec² θ + cosec² θ = [latex]\frac{1}{\cos ^{2} \theta}+\frac{1}{\sin ^{2} \theta}[/latex]
= [latex]\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cdot \cos ^{2} \theta}[/latex]

= [latex]\frac{1}{\sin ^{2} \theta \cdot \cos ^{2} \theta}[/latex]

= [latex]\frac{1}{\sin ^{2} \theta} \cdot \frac{1}{\cos ^{2} \theta}[/latex]

= cosec² θ . sec² θ

These AP 8th Class Biology Important Questions 7th Lesson వివిధ ఆవరణ వ్యవస్థలు will help students prepare well for the exams.

AP Board 8th Class Biology 7th Lesson Important Questions and Answers వివిధ ఆవరణ వ్యవస్థలు

ప్రశ్న 1.
ఆవరణ వ్యవస్థ అన్న పదాన్ని మొదట ఎవరు ఉపయోగించారు ? దాని అర్థం ఏమిటి ?
జవాబు:

1. 1935 సంవత్సరంలో ఎ.జి. టాన్ ప్లే అనే బ్రిటిష్ వృక్ష, ఆవరణ శాస్త్రవేత్త ‘ఆవరణవ్యవస్థ’ ‘Eco system’ అనే పదాన్ని మొదటిసారిగా ఉపయోగించాడు.
2. ప్రకృతి యొక్క మూలప్రమాణాన్ని ఆవరణ వ్యవస్థగా వర్ణించాడు.
3. టాన్ ప్లే పర్యావరణ వ్యవస్థ (Ecological System) ను కుదించి ఆవరణ వ్యవస్థ ‘Eco System’ అని నామకరణం చేశాడు.
4. అతని ప్రకారం ప్రకృతి ఒక వ్యవస్థలాగా పనిచేస్తుంది. అందులోని జీవులు వాటి జాతి సమూహాలు, అనేక నిర్జీవ, వాతావరణ కారకాలు ఒకదానినొకటి తీవ్రంగా ప్రభావితం చేసుకుంటాయి.

ప్రశ్న 2.
ఆవరణ వ్యవస్థలోని శక్తికి సూర్యుడు మూలమని ఎలా చెప్పగలవు ?
జవాబు:

1. ఆవరణ వ్యవస్థలోని ఏ స్థాయి జీవులకైనా బతకడానికి ఆహారం ద్వారా వచ్చే శక్తి అవసరమవుతుంది.
2. సజీవులన్నింటికీ సూర్యుని ద్వారా శక్తి లభిస్తుంది.
3. ఆకుపచ్చని మొక్కలు సూర్యరశ్మిలోని శక్తిని కిరణజన్య సంయోగక్రియ ద్వారా నిక్షిప్తం చేసుకుంటాయి.
4. అయితే జంతువులు మొక్కల మాదిరిగా సూర్యశక్తిని నేరుగా ఉపయోగించుకోలేవు.
5. చాలా రకాల జంతువులు మొక్కలను ఆహారంగా తీసుకుంటాయి.
6. అయితే మొక్కలు ఆహారం తయారుచేసుకోవటానికి సూర్యరశ్మిని ఉపయోగిస్తాయి కాబట్టి ఈ శక్తి మొక్కల నుండి జంతువులకు బదిలీ అవుతుంది.
7. మొక్కలను తినని జంతువులు కూడా సూర్యరశ్మిలోని శక్తి పైనే ఆధారపడతాయి.
8. అవి మొక్కలను తినే జంతువులను తింటాయి. కాబట్టి సూర్యశక్తి బదిలీ అయినట్లే.

ప్రశ్న 3.
ఆహారపు గొలుసు అనగానేమి ? దానిలోని స్థాయిలు ఏమిటి ?
జవాబు:
ఆవరణవ్యవస్థలోని జీవుల మధ్యగల ఆహార సంబంధాలను ఆహార గొలుసు అంటారు. ఆహారపు గొలుసులో మూడు స్థాయిలు ఉంటాయి.
ఉత్పత్తిదారులు : చాలా రకాల మొక్కలు, శైవలాలు మొదలైనవన్నీ సూర్యరశ్మిని ఉపయోగించి ఆహారం తయారు చేసుకుంటాయి. వాటిని ఉత్పత్తిదారులు (Producers) అంటారు.
వినియోగదారులు : ఉత్పత్తిదారులను తిని శక్తిని గ్రహించే జీవులను వినియోగదారులు (Consumers) అంటారు.
విచ్ఛిన్నకారులు : చివరిస్థాయిలో విచ్ఛిన్నకారులు (decomposers) ఉంటాయి. ఇవి మొక్కలు, జంతువులు విసర్జించిన వ్యర్థ పదార్థాల నుండి కాని లేదా వాటి నిర్జీవ పదార్థాల నుండి కానీ ఆహారపదార్థాలను సేకరిస్తాయి.

ప్రశ్న 4.
ఆవాసంలో ఒక జాతి సంఖ్యను మరొక జాతి ఎలా నియంత్రిస్తుంది ? ఉదాహరణతో వివరించండి.
జవాబు:

1. ఆవాసంలో జీవుల మధ్య ఆహార సంబంధాలు ఉంటాయి.
2. ఈ సంబంధాలు జీవుల సంఖ్యను నియంత్రించటంలో తోడ్పడతాయి.
3. ఉదాహరణకి పక్షుల ఆవాసంలో చాలా రకాల కీటకాలు ఉంటాయి. పక్షులు కీటకాలను తినటం వలన కీటకాల సంఖ్య పెరగకుండా చేస్తాయి.
4. దీని వలన పక్షుల ఆవాసం మరియు మొత్తం ఆవరణ వ్యవస్థ ఆరోగ్యకరంగా ఉండి స్థిరంగా ఉంటుంది.
5. కానీ కీటకాలు తినే పక్షుల సంఖ్య ఎక్కువ అయితే కీటకాల సంఖ్య తొందరగా తగ్గిపోతుంది తద్వారా పక్షులకు సరిపడే ఆహారం దొరకదు.
6. ఇటువంటి సందర్భాలలో పక్షులు వేరే ప్రాంతాలకు వలస వెళ్ళిపోతాయి లేదా చనిపోతాయి.
7. వాటి స్థానంలో కొన్ని కొత్త ఆహారపు అలవాట్లు కలిగిన పక్షులు పుట్టడం వలన తిరిగి ఆవరణవ్యవస్థ సమతాస్థితిలోకి వస్తుంది.

ప్రశ్న 5.
మానవ ప్రమేయం ఆధారంగా ఆవరణవ్యవస్థల వర్గీకరణను ఫ్లోచార్టులో చూపండి.
జవాబు:

ప్రశ్న 6.
మాంగ్రూవ్ అడవుల గురించి రాయండి.
జవాబు:

1. భూమిపైన విస్తరించిన ఆవరణ వ్యవస్థలో మాంగ్రూవ్స్ లేదా మడ అడవులు ప్రముఖమైనవి.
2. ఇవి వెనుకకు తన్నిన సముద్రపు నీటితో నిండిన (Back water) లోతు తక్కువ ప్రాంతాలలోనూ, నదులు, సముద్ర జలాలు కలిసే చోట మడ అడవులు విస్తారంగా పెరుగుతాయి.
3. వీటిని మంచి ఉత్పాదక ఆవరణవ్యవస్థగా పేర్కొనవచ్చు.
4. ఈ రకమైన అడవులు తనకు కావల్సిన పోషకాలను భూమిపై పొరలలో ఉన్న మంచినీటి నుంచి, సముద్ర అలల ఉప్పునీటి నుండి గ్రహిస్తాయి.
5. మాంగ్రూవ్స్ వాణిజ్యపరమైన ప్రాధాన్యత గల సముద్ర జీవులకు ముఖ్యమైన ఆహారంగా, నర్సరీలుగా, ప్రజనన స్థలంగా ఉపయోగపడతాయి.
6. అంతే కాకుండా కనుమరుగయ్యే జాతులకు రక్షిత ప్రాంతాలుగా కూడా ఉపయోగపడతాయి.

ప్రశ్న 7.
కోరింగ మాంగ్రూవ్స్ అనగానేమి ? వాటికి ఆ పేరు ఎలా వచ్చింది ?
జవాబు:
కోరింగ మాంగ్రూవ్స్ (మడ అడవులు) కాకినాడ దక్షిణ సముద్రతీరంలో విశాఖపట్టణ దక్షిణ ప్రాంతం నుండి దాదాపుగా 150 కి.మీ. దూరం విస్తరించి ఉన్నాయి. కోరంగై నది పేరుమీద ఈ మాంగ్రూవకు కోరింగ అని పేరుపెట్టారు. కోరింగ మాంగ్రూవ్స్ గౌతమీ, గోదావరి ఉపనదులైన కోరింగ, గాడేరు నదుల నుండి మంచినీటిని తీసుకుంటాయి. అదేవిధంగా కాకినాడ సముద్రతీరం నుంచి ఉప్పునీటిని తీసుకుంటాయి. అనేక నదీ పాయలు, కాలువలు ఈ ఆవరణవ్యవస్థ గుండా ప్రవహిస్తాయి.

ప్రశ్న 8.
కోరింగ ఆవరణవ్యవస్థలో ఉండే సజీవ, నిర్జీవ అంశాలను తెలపండి.

జవాబు:
కోరింగ ఆవరణవ్యవస్థలో ఉండే సజీవ, నిర్జీవ అంశాలు :
జీవ అంశాలలో ఉత్పత్తిదారులు, వినియోగదారులు, విచ్ఛిన్నకారులు ఉంటాయి.

• ఉత్పత్తిదారులు : మడచెట్లు, స్పైరోగైరా, యూగ్లీనా, ఆసిల్లటోరియా, నీలిఆకుపచ్చ శైవలాలు, యూలోథిక్స్ మొదలైన ఉత్పత్తిదారులుంటాయి.
• వినియోగదారులు : పీతలు, హైడ్రా, ప్రోటోజోవాలు, నత్తలు, తాబేళ్ళు, డాఫ్నియా, గొట్టం పురుగులు మొదలైనవి ఉంటాయి.
• విచ్ఛిన్నకారులు : డెట్రిటస్ వంటి విచ్ఛిన్నకర బ్యాక్టీరియాలుంటాయి.
• నిర్జీవ అంశాలు : ఉప్పునీరు, మంచినీరు, గాలి, సూర్యరశ్మి, మృత్తిక మొదలైనవి.

ప్రశ్న 9.
ఎడారి ఆవరణవ్యవస్థలో ఉత్పత్తిదారుల అనుకూలనాలు ఏమిటి ?

జవాబు:

1. పొదలు, గడ్డిజాతులు, కొన్ని వృక్షాలు ఎడారిలో ఉత్పత్తిదారులుగా ఉంటాయి.
2. ఇక్కడి పొదలు భూమి లోపలికి వ్యాపించిన శాఖాయుతమైన వేరు వ్యవస్థ కలిగి ఉంటాయి.
3. కాండాలు, పత్రాలు రూపాంతరం చెంది ముళ్ళుగా లేదా మందంగా మారి ఉంటాయి.
4. ఎడారుల్లో కనబడే కాక్టస్ (బ్రహ్మజెముడు) లాంటి మొక్కల కాండాలు రసభరితంగా మారి నీటిని నిలువ చేసుకొని ఉంటాయి.
5. నీటికొరత ఉన్నప్పుడు ఆ నీటిని వినియోగించుకుంటాయి.
6. కొన్ని నిమ్నశ్రేణి రకాలైన లైకెన్లు, ఎడారి మాన్లు, నీటి ఆకుపచ్చ శైవలాలు కూడా ఎడారులలో కనబడతాయి.

ప్రశ్న 10.
ఆవరణ వ్యవస్థలోని శక్తి ప్రవాహం గురించి రాయండి.
జవాబు:
ఆవరణ వ్యవస్థలోని శక్తి ప్రవాహం :

1. సజీవ ప్రపంచ మనుగడ అనేది ఆవరణవ్యవస్థలో శక్తి ప్రవాహం , పదార్థాల ప్రసరణ పై ఆధారపడి ఉంటుంది.
2. వివిధ రకాల జీవక్రియలు నిర్వహించడానికి శక్తి అవసరం.
3. ఈ శక్తి సూర్యుని నుండి లభిస్తుంది. అంతరిక్షంలో సౌరశక్తి సూర్యకిరణాల రూపంలో ప్రసరిస్తుంది.
4. సౌరశక్తిలో దాదాపు 57% వాతావరణంలో శోషించబడుతుంది మరియు అంతరిక్షంలో వెదజల్లబడుతుంది.
5. 35% సౌరశక్తి భూమిని వేడిచేయడానికి, నీటిని ఆవిరిచేయడానికి ఉపయోగపడుతుంది.
6. దాదాపు 8% సౌరశక్తి మొక్కలకు చేరుతుంది. దీని 80-85% సౌరశక్తిని మొక్కలు శోషిస్తాయి.
7. శోషించిన దానిలో 50% మాత్రమే కిరణజన్య సంయోగక్రియలో వినియోగించబడుతుంది.

ప్రశ్న 11.

ఆకు గొంగళి పురుగు ఊసరవెల్లి పాము గ్రద్ద పైన ఇచ్చిన పటం ఆధారంగా, ఆహారపు గొలుసులోని జీవులను ఉత్పత్తిదారులు, ప్రాథమిక, ద్వితీయ, తృతీయ మరియు ఉన్నత స్థాయి వినియోగదారులుగా వర్గీకరించండి.
జవాబు:
పైన చూపబడిన ఆహారపు గొలుసులో

1. ఆకు – ఉత్పత్తిదారుడు
2. గొంగళిపురుగు – ప్రథమ వినియోగదారుడు
3. ఊసరవెల్లి – ద్వితీయ వినియోగదారుడు
4. పాము – తృతీయ వినియోగారుడు
5. గ్రద్ద – ఉన్నత స్థాయి మాంసాహారి

ప్రశ్న 12.
ఆవరణ వ్యవస్థలోని రకాలను సూచించే ఫ్లోచార్టను గీయండి. ఆవరణవ్యవస్థ పేరు పెట్టినది ఎవరు ?
జవాబు:

“ఆవరణ వ్యవస్థ” అను పదాన్ని ప్రవేశపెట్టినది A.G. టాన్ ప్లే.”

ప్రశ్న 13.
కింది పేరాను చదవండి. కింది ప్రశ్నలకు సమాధానాలు రాయండి.
చాలారకాల మొక్కలు, శైవలాలు మొదలైనవన్నీ సూర్యరశ్మిని ఉపయోగించుకొని ఆహారం తయారుచేసుకుంటాయి. , వాటిని ‘ఉత్పత్తి దారులు’ అంటారు. వీటిని తిని శక్తిని గ్రహించే జీవులను వినియోగదారులు అంటారు. చివరిస్థాయిలో విచ్ఛిన్నకారులు ఉంటారు. ఇవి మొక్కలు, జంతువులు విసర్జించిన వ్యర్థ పదార్థాలనుండి కాని లేదా వాటి నిర్జీవ పదార్థాలనుండి కానీ ఆహారాన్ని సేకరిస్తాయి. వీటిని పునరుత్పత్తిదారులు అంటాం.
1. ఆహారజాలకంలోని ఉత్పత్తిదారులు ఏవి ? వాటిని ఎందుకు ఉత్పత్తిదారులు అంటారు ?
2. వినియోగదారులు అంటే ఏమి ? కొన్ని ఉదాహరణలు ఇవ్వండి.
3. పునరుత్పత్తిదారులు ఏవి ? ఎందుకు వాటిని అలా పిలుస్తారో ఉదాహరణతో వివరించండి.
4. ఆహారపు గొలుసులో ఎన్ని స్థాయిలు ఉంటాయి ? అవి ఏవి ?
జవాబు:
1. శైవలాలు, మొక్కలు ఆహార జాలకంలో ఉత్పత్తిదారులుగా ఉంటాయి. ఎందుకంటే అవి సూర్యరశ్మిని వినియోగించుకొని స్వయంగా ఆహారాన్ని తయారు చేసుకుంటాయి.
2. ఉత్పత్తిదారులను ఆహారంగా స్వీకరించి శక్తిని గ్రహించే జీవులను వినియోగదారులు అంటారు. ఉదా : జింక, మిడత, కుందేలు
3. విచ్ఛిన్నకారులుగా పూతికాహార బాక్టీరియా శిలీంధ్రాలు ఉంటాయి. ఇవి మొక్కల జంతువుల నిర్జీవ పదార్థాల నుండి ఆహారాన్ని సేకరిస్తాయి. వాటిని మూలకాలుగా విడగొట్టి తిరిగి ఆవరణ వ్యవస్థలో ప్రవేశపెడతాయి. అందువల్ల వీటిని పునరుత్పత్తి. దారులు అంటారు.
4. ఆహారపు గొలుసులో 4 స్థాయిలు ఉంటాయి.
ఉత్పత్తిదారులు ప్రాథమిక వినియోగదారులు ద్వితీయ వినియోగదారులు తృతీయ వినియోగదారులు

ప్రశ్న 14.
క్రింది అంశంను చదివి ప్రశ్నలకు జవాబులిమ్ము.
భూభాగంలో దాదాపు 17% మేర ఎడారులు విస్తరించి ఉన్నాయి. ఈ ప్రాంతంలో ఇసుకతో కూడిన నేల ఉండి సగటు వర్షపాతం 23 మి.మీల కన్నా తక్కువగా ఉంటుంది. ఇక్కడ పెరిగే మొక్కలు నీటిని నష్టపోకుండా అనుకూలనాలు కలిగి ఉంటాయి. అత్యధిక ఉష్ణోగ్రత వలన ఇక్కడ జీవజాతులు ప్రత్యేక లక్షణాలను కలిగి ఇక్కడి వాతావరణానికి అనుకూలనాలు పొంది ఉంటాయి.
1. ఎడారి జీవులు ఎలాంటి అనుకూలనాలను పొంది ఉండాలి ?
2. ఉత్పత్తిదారులైన ఎడారి మొక్కలు చూపే అనుకూలనాలేవి ?
3. ఒంటెను ఎడారి ఓడ అని ఎందుకు అంటారు ?
4. ఎడారుల్లో జంతువైవిధ్యం తక్కువగా ఉంటుంది. ఎందుకు ?
జవాబు:
1. అక్కడి అధిక ఉష్ణోగ్రతలకు నీరు నష్టపోకుండా అనుకూలనాలను కలిగి ఉంటుంది.
2. ఎడారి మొక్కలు పత్రరంధ్రాలను కలిగి ఉండవు. అందువల్ల భాష్పోత్సేకం ద్వారా నీటిని నష్టపోవు.
3. ఒంటె ఎడారి వాతావరణాన్ని ఎన్నో అనుకూలనాలను కల్గి ఎడారిలో ప్రయాణానికి ఎంతో అనువైన జంతువు. అందువల్ల ఒంటెను ఎడారి ఓడ అని అంటారు.
4. ఎడారిలో ఉండే అత్యధిక ఉష్ణోగ్రతలను నీటి ఎద్దడిని తట్టుకొని జీవించడం చాలా కష్టం. అందువలన అక్కడ జంతు వైవిధ్యం తక్కువ.

ప్రశ్న 15.
మీ పరిసరాలలో మీరు గమనించి ఉత్పత్తిదారులు, వినియోగదారుల జాబితాలను తయారు చేయండి.
జవాబు:
నా పరిసరాలలో నేను గమనించిన ఆహార జాలకం

1 మార్కు ప్రశ్నలు

ప్రశ్న 1.
ఆహారపు గొలుసు అంటే ఏమిటి?
జవాబు:
ఉత్పత్తిదారుడు, ప్రథమ, ద్వితీయ, తృతీయ వినియోగదారులు ఉన్న గొలుసు లాంటి జంతువుల శక్తి మార్పిడి వ్యవస్థను ‘ఆహారపు గొలుసు’ అంటారు.

ప్రశ్న 2.
‘ఆహార జాలకం’ అంటే ఏమిటి?
జవాబు:
అనేక ‘ఆహారపు గొలుసులు’ ఒక దానిలో ఒకటి కలిసిపోయి ఒక సమూహంగా, ఆవరణ వ్యవస్థలో కొనసాగే క్రియాత్మక, వ్యవస్థను ‘ఆహార జాలకం’ అంటారు.

ప్రశ్న 3.
ఆహార జాలకంలోని మొక్కలు చనిపోతే ఏమవుతుంది ?
జవాబు:
1. ఆహార జాలకంలోని మొక్కలు చనిపోతే శక్తిని ఉత్పత్తిచేసే.అవకాశం పోతుంది.
2. దీనితో సూర్యరశ్మి నుంచి శక్తి బదలాయింపు ఆగిపోతుంది.
3. కొంత కాలం తర్వాత నెమ్మదిగా క్రింది స్థాయి నుంచి ఉన్నతస్థాయి జీవులన్నీ అంతరించిపోతాయి.

ప్రశ్న 4.
ఆహారం ఒక్కటే కాకుండా జంతువులు బ్రతకటానికి కావల్సిన ఇతర అంశాలు ఏమిటి ?
జవాబు:
జంతువులకు ఆహారంతో పాటు
1. నీరు
2. గాలి
3. ఆవాసం బతకటానికి కావాల్సి ఉంటుంది.

లక్ష్యాత్మక నియోజనము

ప్రశ్న 1.
గడ్డిని ……….. గా పిలవవచ్చు.
ఎ) వినియోగదారు
బి) ఉత్పత్తిదారు
బి) విచ్ఛిన్నకారి
డి) బాక్టీరియా
జవాబు:
బి) ఉత్పత్తిదారు

ప్రశ్న 2.
కొన్ని ఆహారపు గొలుసుల కలయిక వల్ల ……….. ఏర్పడును.
ఎ) ఆహార జాలకం
బి) ఆవాసం
సి) జీవావరణం
డి) ప్రకృతి
జవాబు:
ఎ) ఆహార జాలకం

ప్రశ్న 3.
నెమలికి ఇష్టమైన ఆహారం ………..
ఎ) బల్లులు
బి) పురుగులు
సి) పాములు
డి) కీటకాలు
జవాబు:
సి) పాములు

ప్రశ్న 4.
కోరింగ మడ అడవులు ………. పట్టణానికి సమీపంలో ఉన్నాయి.
ఎ) రాజమండ్రి
బి) కాకినాడ
సి) విజయవాడ
డి) హైదరాబాద్
జవాబు:
బి) కాకినాడ

ప్రశ్న 5.
భూభాగంలో ………. % మేరకు ఎడారి ఆవరణ వ్యవస్థలు ఉన్నాయి.
ఎ) 14
బి) 15
సి) 16
డి) 17
జవాబు:
డి) 17

ప్రశ్న 6.
ఇది గోదావరికి ఉపనది. ఆ
ఎ) పాములేరు
బి) గాడేరు
సి) బుడమేరు
డి) పాలవాగు
జవాబు:
డి) పాలవాగు

ప్రశ్న 7.
నిశాచరాలకు ఉదాహరణ ……….
ఎ) గేదె
బి) ఆవు
సి) గుడ్లగూబ
డి) మానవుడు
జవాబు:
ఎ) గేదె

ప్రశ్న 8.
ఒంటె శరీరంలోని ……….. భాగంలో నీరు దాచు కుంటుంది.
ఎ) నోరు
బి) చర్మం
సి) జీర్ణాశయం
డి) కాలేయం
జవాబు:
సి) జీర్ణాశయం

ప్రశ్న 9.
సూర్యకాంతి ………. చే శోషింపబడుతుంది.
ఎ) జంతువులు
బి) మొక్కలు
సి) సరీసృపాలు
డి) క్షీరదాలు
జవాబు:
బి) మొక్కలు

ప్రశ్న 10.
సింహం ………. శ్రేణి మాంసాహారి.
ఎ) ప్రాథమిక
బి) ద్వితీయ
సి) తృతీయ
డి) చతుర్ధ
జవాబు:
సి) తృతీయ

ప్రశ్న 11.
ఆవరణ వ్యవస్థ అనే పదాన్ని 1935 సం||లో మొదటిసారిగా ఉపయోగించిన శాస్త్రవేత్త
ఎ) చార్లెస్ ఎల్టన్
బి) యూజీస్ పి.ఓడమ్
సి) A.C. టాన్స్లే
డి) చార్లెస్ డార్విన్
జవాబు:
సి) A.C. టాన్స్లే

ప్రశ్న 12.
ఆవరణ వ్యవస్థలోని అతిపెద్ద భాగం
ఎ) ఆవాసం
బి) పర్యావరణం
సి) జీవావరణం
డి) నివాసం
జవాబు:
ఎ) ఆవాసం

ప్రశ్న 13.
ఆవరణ వ్యవస్థలో శక్తికి మూలం
ఎ) ఆహారం
బి) ఆకుపచ్చని మొక్కలు
సి) సూర్యుడు
డి) భూమి
జవాబు:
సి) సూర్యుడు

ప్రశ్న 14.
ఆవరణ వ్యవస్థలో నిర్జీవ అంశం కానిది
ఎ) గాలి
బి) నీరు
సి) మృత్తిక
డి) సూక్ష్మజీవులు
జవాబు:
డి) సూక్ష్మజీవులు

ప్రశ్న 15.
ఆవరణ వ్యవస్థలో సూర్యరశ్మిని నేరుగా గ్రహించగలిగేవి
ఎ) ఉత్పత్తిదారులు
బి) ప్రాథమిక వినియోగదారులు
సి) ద్వితీయ వినియోగదారులు
డి) విచ్ఛిన్నకారులు
జవాబు:
ఎ) ఉత్పత్తిదారులు

ప్రశ్న 16.
ఆవరణ వ్యవస్థలో పునరుత్పత్తిదారులు అని వేనిని అంటారు?
ఎ) ఉత్పత్తిదారులు
బి) ప్రాథమిక వినియోగదారులు
సి) ద్వితీయ వినియోగదారులు
డి) విచ్చిన్నకారులు
జవాబు:
డి) విచ్చిన్నకారులు

ప్రశ్న 17.
ఆవరణ వ్యవస్థలో చివరి స్థాయి జీవులు
ఎ) విచ్ఛిన్నకారులు
బి) ప్రాథమిక వినియోగదారులు
సి) ద్వితీయ వినియోగదారులు
డి) తృతీయ వినియోగదారులు
జవాబు:
ఎ) విచ్ఛిన్నకారులు

ప్రశ్న 18.
ఆవరణ వ్యవస్థలో శక్తి బదిలీ విధానాన్ని వివరించడానికి ఉపయోగపడేది
ఎ) పోషకస్థాయి
బి) ఎకలాజికల్ నిచ్
సి) ఆహారపు గొలుసు
డి) ఆహారపు జాలకం
జవాబు:
సి) ఆహారపు గొలుసు

ప్రశ్న 19.
ఆవరణ వ్యవస్థను తొందరగా నాశనం చేసేవి
ఎ) బలమైన గాలులు
బి) భూకంపాలు
సి) సునామి
డి) పైవన్నీ
జవాబు:
డి) పైవన్నీ

ప్రశ్న 20.
భూమిపై ఉండే అతి పెద్ద ఆవరణ వ్యవస్థ
ఎ) జీవావరణం
బి) పర్యావరణం
సి) భౌమావరణం
డి) జలావరణం
జవాబు:
ఎ) జీవావరణం

ప్రశ్న 21.
మడ అడవులు యిక్కడ పెరుగుతాయి.
ఎ) నది ఒడ్డున
బి) సముద్రం ఒడ్డున
సి) నది, సముద్రం కలిసే చోట
డి) సముద్రం సముద్రం కలిసే చోట
జవాబు:
సి) నది, సముద్రం కలిసే చోట

ప్రశ్న 22.
ఆహారపు జాలకాన్ని ఏర్పరిచేవి
ఎ) ఉత్పత్తిదారులు
బి) వినియోగదారులు
సి) విచ్ఛిన్నకారులు
డి) ఆహారపు గొలుసులు
జవాబు:
డి) ఆహారపు గొలుసులు

ప్రశ్న 23.
ఈ క్రింది వానిలో కృత్రిమ ఆవరణ వ్యవస్థ
ఎ) గడ్డిభూమి
బి) అడవి
సి) ఎడారి
డి) కార్తీకవనాలు
జవాబు:
డి) కార్తీకవనాలు

ప్రశ్న 24.
కోరింగ వద్ద ఉన్న ఆవరణ వ్యవస్థ
ఎ) గడ్డిభూమి ఆవరణ వ్యవస్థ
బి) మాంగ్రూప్ ఆవరణ వ్యవస్థ
సి) అడవి ఆవరణ వ్యవస్థ
డి) ఎడారి ఆవరణ వ్యవస్థ
జవాబు:
బి) మాంగ్రూప్ ఆవరణ వ్యవస్థ

ప్రశ్న 25.
ఈ క్రింది వానిలో సహజ ఆవరణ వ్యవస్థ
ఎ) మామిడి తోట
బి) వరి చేను
సి) కార్తీకవనం
డి) ఎడారి
జవాబు:
డి) ఎడారి

ప్రశ్న 26.
ఇండో పసిఫిక్ సముద్రంలో ఒక చదరపు కిలోమీటర్ విస్తీర్ణంలో ఎన్ని జీవజాతులున్నాయి ?
ఎ) 10
బి) 100
సి) 1000
డి) 10,000
జవాబు:
సి) 1000

ప్రశ్న 27.
అత్యధిక జీవులు యిక్కడ ఉన్నాయి.
ఎ) నేల
బి) నది
సి) సముద్రం
డి) అడవి
జవాబు:
సి) సముద్రం

ప్రశ్న 28.
ఈ క్రింది వానిలో ఆవరణ వ్యవస్థ కానిది
ఎ) ఒక దుంగ
బి) ఒక గ్రామం
సి) ఒక అంతరిక్ష నౌక
డి) పైవేవీ కావు
జవాబు:
డి) పైవేవీ కావు

ప్రశ్న 29.
ప్రకృతి యొక్క క్రియాత్మక ప్రమాణం అని దీనిని అనవచ్చు.
ఎ) ఆవరణ వ్యవస్థ
బి) జీవావరణం
సి) పర్యావరణం
డి) ఆవాసం
జవాబు:
ఎ) ఆవరణ వ్యవస్థ

ప్రశ్న 30.
భూభాగంలో ఎంత శాతం ఎడారులు విస్తరించి ఉన్నాయి ?
ఎ) 7%
బి) 17%
సి) 27%
డి) 37%
జవాబు:
బి) 17%

ప్రశ్న 31.
ఎడారులలో వర్షపాతం ఇంతకన్నా తక్కువ.
ఎ) 10 మిల్లీ మీటర్లు
బి) 17 మిల్లీ మీటర్లు
సి) 20 మిల్లీ మీటర్లు
డి) 23 మిల్లీ మీటర్లు
జవాబు:
డి) 23 మిల్లీ మీటర్లు

ప్రశ్న 32.
నిశాచరులు యిక్కడ ఎక్కువగా ఉంటాయి
ఎ) గడ్డిభూమి ఆవరణ వ్యవస్థ
బి) మంచినీటి ఆవరణ వ్యవస్థ
సి) ఎడారి ఆవరణ వ్యవస్థ
డి) పైవేవీ కావు
జవాబు:
సి) ఎడారి ఆవరణ వ్యవస్థ

ప్రశ్న 33.
అటవీ పరిసరాలను ప్రభావితం చేసేవి
ఎ) శీతోష్ణస్థితి
బి) పోషకాల క్రియాశీలత
సి) నీటివనరులు
డి) పైవన్నీ
జవాబు:
డి) పైవన్నీ

ప్రశ్న 34.
మొత్తం సౌరశక్తిలో వాతావరణంలోకి శోషించబడే సౌరశక్తి, భూమిని వేదిచేయడానికి కావలసిన శక్తి, మొక్కలు గ్రహించే సౌరశక్తి వరుసగా
ఎ) 67%, 35%, 8%
బి) 8%, 35%, 57%
సి) 57%, 8%, 355
డి) 35%, 8%, 57%
జవాబు:
ఎ) 67%, 35%, 8%

ప్రశ్న 35.
సౌరశక్తి ఉత్పత్తిదారులలో ఈ రూపంలో నిల్వ ఉంటుంది.
ఎ) గతిశక్తి
బి) స్థితిశక్తి.
సి) ఉష్ణశక్తి
డి) అయానికశక్తి
జవాబు:
బి) స్థితిశక్తి.

ప్రశ్న 36.
ఆహారపు గొలుసులోని సరియైన వరుసక్రమాన్ని గుర్తించండి.
ఎ) ఉత్పత్తిదారులు → ప్రాథమిక వినియోగదారులు → ద్వితీయ వినియోగదారులు → విచ్ఛిన్నకారులు
బి) ప్రాథమిక వినియోగదారులు → ద్వితీయ వినియోగదారులు → ఉత్పత్తిదారులు → విచ్ఛిన్నకారులు
సి) విచ్ఛిన్నకారులు → ప్రాథమిక వినియోగదారులు → ద్వితీయ వినియోగదారులు → ఉత్పత్తిదారులు
డి) ఉత్పత్తిదారులు → విచ్ఛిన్నకారులు → ప్రాథమిక వినియోగదారులు → ద్వితీయ వినియోగదారులు
జవాబు:
ఎ) ఉత్పత్తిదారులు → ప్రాథమిక వినియోగదారులు → ద్వితీయ వినియోగదారులు → విచ్ఛిన్నకారులు

ప్రశ్న 37.
ఆహారపు గొలుసులో స్థాయిల సంఖ్య
ఎ) 1
బి) 2
సి) 3
డి) 4
జవాబు:
సి) 3

ప్రశ్న 38.
ఆవరణ వ్యవస్థలో మాంసాహారులు
ఎ) ఉత్పత్తిదారులు
బి) విచ్ఛిన్నకారులు
సి) ప్రాథమిక వినియోగదారులు
డి) ద్వితీయ వినియోగదారులు
జవాబు:
డి) ద్వితీయ వినియోగదారులు

ప్రశ్న 39.
ఉత్పత్తిదారులలో నిక్షిప్తమైన శక్తి
ఎ) మొత్తం ప్రాథమిక ఉత్పత్తి
బి) మిగిలిన ప్రాథమిక ఉత్పత్తి,
సి) వినియోగించబడని శక్తి
డి) వినియోగదారులచే శోషించబడని శక్తి
జవాబు:
ఎ) మొత్తం ప్రాథమిక ఉత్పత్తి

ప్రశ్న 40.
కాక్టస్ ఇక్కడ కనిపిస్తుంది.
ఎ) గడ్డిభూమి
బి) అడవి
సి) ఎడారి
డి) నది
జవాబు:
సి) ఎడారి

ప్రశ్న 41.
ఒంటె శరీరంలో నీటిని ఎక్కడ నిల్వ ఉంచుకుంటుంది ?
ఎ) మూపురం
బి) చర్మం క్రింద
సి) జీర్ణాశయం
డి) కాలేయం
జవాబు:
సి) జీర్ణాశయం

ప్రశ్న 42.
ఒక ఆవరణ వ్యవస్థలో కింది వాటిలోని ఏ జత జీవులు ఉత్పత్తిదారులుగా వుంటాయి ?
(A) ఎంప్, స్పైరోగైరా
(B) మస్సెల్, డాఫియా
(C) అసిల్లటోరియా, యులోత్రిక్స్
(D) యూగ్లీనా, బ్యాక్టీరియా
జవాబు:
(C) అసిల్లటోరియా, యులోత్రిక్స్

ప్రశ్న 43.
1. ఉత్పత్తిదారులకు ఉదాహరణ గడ్డిజాతులు
2. వినియోగదారులకు ఉదాహరణ గ్రద్దలు
(A) 1, 2 సరైనవి కావు
(B) 1 సరైనది, 2 కాదు
(C) 1, 2 సరైనవి
(D) 1 సరైనదికాదు 2 సరైనది
జవాబు:
(C) 1, 2 సరైనవి

ప్రశ్న 44.
ఎడారి ఓడ అని పిలవబడే జీవి
(A) ఏనుగు
(B) ఒంటె
(C) నిప్పు కోడి
(D) కంచర గాడిద
జవాబు:
(B) ఒంటె

ప్రశ్న 45
ఎడారి జంతువులు కలిగి ఉండేవి
(A) బాహ్య అనుకూలనాలు
(B) శరీరధర్మ అనుకూలనాలు
(C)ఏ అనుకూలనాలు ఉండవు
(D) బాహ్య మరియు శరీరధర్మ అనుకూలనాలు
జవాబు:
(D) బాహ్య మరియు శరీరధర్మ అనుకూలనాలు

ప్రశ్న 46.
ఒకేసారి అధిక సంఖ్యలో కుందేళ్ళను గడ్డిభూముల్లో ప్రవేశపెడితే జరిగేది
(A) అధిక సంఖ్యలో కుందేళ్ళు కనిపిస్తాయి
(B) కుందేళ్ళ మధ్య ఆహారం కోసం తీవ్రమైన పోటీ ఏర్పడుతుంది
(C) ఆవరణ వ్యవస్థలో ఎలాంటి మార్పు ఉండదు
(D) గడ్డి పెరగడంపై ఏ ప్రభావం ఉండదు
జవాబు:
(B) కుందేళ్ళ మధ్య ఆహారం కోసం తీవ్రమైన పోటీ ఏర్పడుతుంది

ప్రశ్న 47.
భౌమావరణ వ్యవస్థలోని మొక్కల్లో పత్రరంధ్రాలు లేకపోతే ఇరిగేది
(A) భాష్పోత్సేకం జరగదు
(B) వాయువినిమయం జరగదు ,
(C) మొక్కలపై ఏ ప్రభావం ఉండదు
(D) A మరియు B
జవాబు:
(D) A మరియు B

ప్రశ్న 48.
భూ ఆవరణ వ్యవస్థలో P, Q మరియు ఎడారి ఆవరణ వ్యవస్థలు ఉంటాయి. ఇందులో P,Qలు
(A) అడవి, గడ్డిభూమి
(B) గడ్డి భూమి, కొలను
(C) మంచినీరు, ఉప్పునీరు
(D) అడవి, ఉప్పునీరు
జవాబు:
(A) అడవి, గడ్డిభూమి

These AP 10th Class Maths Chapter Wise Important Questions 10th Lesson క్షేత్రమితి will help students prepare well for the exams.

AP Board 10th Class Maths 10th Lesson Important Questions and Answers క్షేత్రమితి

ప్రశ్న 1.
7 సెం.మీ. వ్యాసార్ధం గల అర్ధగోళ సంపూర్ణతల – వైశాల్యంను కనుగొనుము.
సాధన.
అర్ధగోళం వ్యాసార్ధం r = 7 సెం.మీ.
అర్ధగోళ సంపూర్ణతల వైశాల్యం = 3πr²
= 3 × [latex]\frac{22}{7}[/latex] × 7 × 7
= 462 చ. సెం.మీ.

ప్రశ్న 2.
3 సెం.మీ. వ్యాసార్ధము మరియు 14 సెం.మీ. ఎత్తు కల్గిన క్రమ వృత్తాకార శంఖువు యొక్క ఘనపరిమాణం కనుగొనండి.
సాధన.
శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 3 × 3 × 14
= 132 సెం.మీ.³

ప్రశ్న 3.
7 సెం.మీ. వ్యాసార్ధము మరియు 10 సెం.మీ. ఎత్తు కలిగిన స్థూపం యొక్క వక్రతల వైశాల్యము కనుగొనండి.
సాధన.
2స్థూపం యొక్క వ్యాసార్ధము (r) = 7 సెం.మీ.
ఎత్తు (h) = 10 సెం.మీ. స్థూపం యొక్క వక్రతల వైశాల్యం = 2πrh
= 2 × [latex]\frac{22}{7}[/latex] × 7 × 10
= 440 చ.సెం.మీ.

ప్రశ్న 4.
ఒక ఫుట్ బాల్ యొక్క ఉపరితల వైశాల్యము 616 చ.సెం.మీ. అయిన ఆ బంతి వ్యాసార్ధమును కనుగొనుము. (π = 22/7)
సాధన.
ఒక ఫుట్ బాల్ యొక్క ఉపరితల వైశాల్యము (గోళం) = 4πr²
4πr² = 616
πr² = 154
r² = 154 × [latex]\frac{7}{22}[/latex]
r² = 7 × 7 = 49
∴ r = 7 సెం.మీ.

ప్రశ్న 5.
ఒక స్థూపము యొక్క ఘనపరిమాణము 4481 సెం.మీ. 3 మరియు ఎత్తు 7 సెం.మీ. అయిన స్థూపము యొక్క వ్యాసార్ధము కనుగొనుము.
సాధన.
స్థూపము ఘనపరిమాణము = πr²h = 448π
ఇచ్చట h = 7 సెం.మీ. , r = r
πr² × 7 = 448π
7r² = 448
r² = [latex]\frac{448}{7}[/latex] = 64
∴ వ్యాసార్ధము (r) = 8 సెం.మీ.

ప్రశ్న 6.
ఒక గోళము యొక్క వ్యాసార్ధము 14 సెం.మీ. అయిన దాని ఉపరితల వైశాల్యం కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము)
సాధన.
గోళము యొక్క వ్యాసార్ధము = (r) = 14 సెం.మీ.
గోళఉపరితల వైశాల్యమునకు సూత్రము = 4πr²
∴ గోళ ఉపరితల వైశాల్యము = 4 × [latex]\frac{22}{7}[/latex] × 14 × 14
= 88 × 28
= 2464 సెం.మీ.²

ప్రశ్న 7.
సమాన భూ వ్యాసార్ధము కలిగిన శంఖువు మరియు స్టూపములను జతగా కలుపగా ఏర్పడే ఘనాకార వస్తువు యొక్క చిత్తు పటమును గీయుము.
సాధన.

శంఖువు మరియు స్థూపముల సమాన భూవ్యాసార్ధము = AB

ప్రశ్న 8.
7 సెం.మీ. వ్యాసార్ధం, 14 సెం.మీ. ఏటవాలు ఎత్తు కలిగిన ఒక శంఖాకార జోకర్ క్యాప్ తయారు చేయడానికి అవసరమైన పేపర్ షీటు యొక్క వైశాల్యం కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, వ్యాసార్ధం = 7 సెం.మీ.
ఏటవాలు ఎత్తు = 14 సెం.మీ.
పేపర్ షీటు యొక్క వైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 7 × 14
= 22 × 14 = 308 సెం.మీ.²

ప్రశ్న 9.
ఒక గోళం యొక్క వ్యాసం, ఘనం యొక్క భుజంకు సమానం అయితే, వాటి ఘనపరిమాణాల నిష్పత్తిని కనుగొనుము.
సాధన.
గోళం యొక్క వ్యాసం = d = ఘనం యొక్క భుజం అనుకొనుము.
∴ గోళం యొక్క వ్యాసార్ధం (r) = [latex]\frac{d}{2}[/latex],
గోళం యొక్క ఘనపరిమాణం = [latex]\frac{4}{3}[/latex] πr³
= [latex]\frac{4}{3} \pi\left(\frac{d}{2}\right)^{3}=\frac{4}{3} \pi \frac{d^{3}}{8}=\frac{\pi}{6} d^{3}[/latex]
మరియు ఘనం యొక్క ఘనపరిమాణం = d³
∴ గోళం ఘనపరిమాణం మరియు ఘనం ఘనపరిమాణాల నిష్పత్తి = [latex]\frac{\pi}{6}[/latex]d³ : d³
= [latex]\frac{\pi}{6}[/latex] : 1

ప్రశ్న 10.
125 ఘనపు సెం.మీ. ఘనపరిమాణం గల రెండు 1 ఘనములు కలుపబడినవి. అప్పుడు ఏర్పడిన దీర్ఘ ఘనము యొక్క సంపూర్ణతల వైశాల్యం ఎంత ?
సాధన.
ఒక ఘనము యొక్క ఘనపరిమాణము = 125 సెం.మీ³
a³ = 125 సెం.మీ.³ = (5 సెం.మీ)³.
∴ ఆ ఘనం యొక్క భుజం = 5 సెం.మీ.
అటువంటి రెండు ఘనములు కలుపబడినపుడు ఏర్పడిన దీర్ఘఘనం యొక్క పొడవు (l) = 10 సెం.మీ.
వెడల్పు (b) = 5 సెం.మీ.
ఎత్తు (h) = 5 సెం.మీ.

∴ దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2 (lb + bh + lh)
= 2[(10 × 5) + (5 × 5) + (5 × 10)]
= 2[50 + 25 + 50]
= 2(125) = 250 సెం.మీ²
∴ రెండు ఘనములు కలుపగా ఏర్పడిన దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 250 సెం.మీ²

ప్రశ్న 11.
ఒక శంకువు యొక్క భూ వైశాల్యం 616 చ.సెం.మీ., దాని ఎత్తు 48 సెం.మీ. అయిన దాని సంపూర్ణతల వైశాల్యం కనుగొనుము.
సాధన.
శంఖువు భూ వ్యాసార్ధం = r సెం.మీ. అనుకొనుము.
మరియు ఎత్తు = h = 48 సెం.మీ.
∴ శంఖువు భూ వైశాల్యం = πr²

= [latex]\frac{22}{7}[/latex] × r² = 616 సెం.మీ²
⇒ r² = [latex]\frac{616 \times 7}{22}[/latex]
= 28 × 7
= 2 × 7 × 2 × 7 = 142
∴ శంఖువు భూ వ్యాసార్ధం r = 14 సెం.మీ.
∴ శంఖువు ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{14^{2}+48^{2}}[/latex]
= [latex]\sqrt{196+2304}=\sqrt{2500}[/latex]
∴ l = 50 సెం.మీ.
శంఖువు సం||తల వైశాల్యము = నేల వైశాల్యము + ప్రక్కతల వైశాల్యము
= πr² + πrl
= πr(r + l)
= [latex]\frac{22}{7}[/latex] × 14 × (14 + 50)
= [latex]\frac{22}{7}[/latex] × 14 × 64
= 44 × 64 = 2816
∴ ఆ శంఖువు సం||తల వైశాల్యము = 2816 సెం.మీ²

ప్రశ్న 12.
ఒక శంఖువు యొక్క శీర్షకోణములో, సగము 60° మరియు దాని ఎతు 3 సెం.మీ. అయిన శంఖువు యొక్క ఘనపరిమాణం కనుగొనుము.
సాధన.
‘B’ అనేది శంఖువు భూ కేంద్రము మరియు
వ్యాసార్ధము = BC
నిలువుటెత్తు AB = 3 సెం.మీ.
∠BAC = 60° అని ఇవ్వబడింది.

∆ABC ఒక లంబకోణ త్రిభుజం,
tan 60° = [latex]\frac{\mathrm{BC}}{\mathrm{AB}}[/latex]
⇒ √3 = B
⇒ BC = 3√3 ‘సెం.మీ.
ఇచ్చట h = 3 సెం.మీ., r = 3√3 సెం.మీ.
శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] π(3√3)² × 3
= 27 πసెం.మీ³
(లేదా)
= [latex]\frac{594}{7}[/latex] = 84.86 సెం.మీ.³

ప్రశ్న 13.
ఒక దీర్ఘ ఘనము యొక్క పొడవు, వెడల్పు, ఎత్తులు వరుసగా (log 125 + log 8), (log 1000 – log 10) మరియు log 10 అయినచో దాని సంపూర్ణతల వైశాల్యము ఎంత ?
సాధన. దీర్ఘఘనము పొడవు (1) = (log 125 + log 8)
దీర్ఘఘనము వెడల్పు (b) = (log 1000 – log 10)
దీర్ఘఘనము ఎత్తు (h) = log 10
∴ (l) = log (125 × 8)
= log 1000
= log 10³ = 3 log 10 = 3
(b) = log 1000 – log 10
= log [latex]\frac{1000}{10}[/latex]
= log 100
= log 10² = 2
(h) = log 10 = 1
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2(lb + bh + lh)
= 2 (3 × 2 + 2 × 1 + 1 × 3)
= 2 (6 + 2 + 3)
= 2(11) = 22 చ|| యూనిట్లు.

ప్రశ్న 14.
ఒక గోళం యొక్క వ్యాసార్థం 3.5 సెం.మీ. దాని ఉపరితల వైశాల్యం కనుగొనుము.
సాధన.
దత్తాంశం ప్రకారం r = 3.5 సెం.మీ.
గోళం యొక్క ఉపరితల వైశాల్యం = 4πr²
= 4 × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5
= [latex]\frac{88 \times 12.25}{7}[/latex]
= 154 సెం.మీ.²

ప్రశ్న 15.
ఒక శంఖువు యొక్క ఘపరిమాణాన్ని అదే ఆధారం మరియు ఎత్తును కలిగిన క్రమవృత్తాకార స్థూపం యొక్క ఘనపరిమాణంలో వ్యక్తీకరించి నీవు దానిని ఎలా చేరుకున్నావో వివరించండి.
సాధన.
శంఖువు యొక్క ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] πr²h
స్థూపం యొక్క ఘనపరిమాణం = πr²h అని మనకు తెలుసు.
కావున, శంఖువు ఘనపరిమాణం : స్థూపం ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] πr² : πr²h
∴ శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] × స్థూపం ఘనపరిమాణం.

ప్రశ్న 16.
శంఖాకారంలో ఉన్న గుడారం భూ వ్యాసార్థం 5 మీ. దాని ఎత్తు 12 మీ. ఆ గుడారం నిర్మించుటకు కావలసిన గుడ్డ వెడల్పు 2 మీ. అయినపుడు పొడవెంత ?
సాధన.
శంఖాకారపు గుడారము వ్యాసార్ధము (r) = 5 మీ.
గుడారము ఎత్తు (h) = 12 మీ.
∴ శంఖువు వాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{5^{2}+12^{2}}[/latex]
= [latex]\sqrt{25+144}=\sqrt{169}[/latex] = 13 మీ.
గుడారపు ప్రక్కతల వైశాల్యం = πrl .
= [latex]\frac{22}{7}[/latex] × 5 × 13 = [latex]\frac{1430}{7}[/latex] చ.మీ.
ఉపయోగింపబడిన కొన్వాసు గుడ్డ ‘వైశాల్యం = [latex]\frac{1430}{7}[/latex] చ.మీ.
కాన్వాసు గుడ్డ వెడల్పు 2 మీ. అని ఇవ్వబడింది.
కనుక కాన్వాసు గుడ్డ పొడవు = వైశాల్యము / వెడల్పు
= [latex]\frac{1430}{7} \times \frac{1}{2}[/latex] = 102.14 మీ.

ప్రశ్న 17.
66 సెం.మీ. భుజము కొలతగా గల ఒక సీసపు ఘనమును 3 సెం.మీ. వ్యాసార్ధము కల్గిన ఎన్ని గోళాకార బంతులుగా మార్చవచ్చు ? ”
సాధన.
ఘనం యొక్క భుజము (s) = 66 సెం.మీ.
గోళాకార బంతి వ్యాసార్ధము (r) = 3 సెం.మీ.
తయారుచేయగల గోళాకార బంతుల సంఖ్య = n అనుకొనుము.
n × గోళాకార బంతి ఘనపరిమాణం = ఘనం ఘనపరిమాణం
⇒ n × [latex]\frac{4}{3}[/latex]πr³ = s³
⇒ n × [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 3 × 3 × 3 = (66)³
⇒ n = 66 × 66 × 66 × [latex]\frac{3}{4} \times \frac{7}{22} \times \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}[/latex]
∴ n = 2541
తయారుచేయగల గోళాకార బంతుల సంఖ్య = 2541.

ప్రశ్న 18.
స్థూపాకృతిలో ఉన్న ‘నూనె పీపా 2 మీ. భూవ్యాసం మరియు 7 మీ. ఎత్తును కల్గియున్నది. పీపాకు రంగు వేయడానికి పెయింటర్ 1 చ.మీ. కు .₹ 5 లను తీసుకుంటుంటే, 10 నూనె పీపాలకు రంగు వేయడానికి ఎంత ఖర్చు అవుతుంది ?
సాధన.

స్థూపాకృతిలో ఉన్న నూనె పీపా భూ వ్యాసం = d = 2 మీ.
పీపా వ్యాసార్ధం = r= 2
ఎత్తు = h = 7 మీ.
స్థూపాకార నూనె పీపా యొక్క సంపూర్ణతల వైశాల్యం = 2πr(r + h)
= 2 × [latex]\frac{22}{7}[/latex] × 1 × (1 + 7)
= 2 × [latex]\frac{22}{7}[/latex] × 8
= [latex]\frac{352}{7}[/latex] = 50.28 చ.మీ.
1 చ.మీ.కు రంగు వేయుటకు ఖర్చు = రూ. 5 అటువంటి 10 పీపాలకు రంగు వేయడానికి అయ్యే ఖర్చు = 50.28 × 5 × 10 = రూ. 2514

ప్రశ్న 19.
ఒక సమ ఘనాకార చెక్కదిమ్మ నుండి దాని భుజము పొడవునకు సమాన పొడవు వ్యాసముగా కల్గిన అర్ధగోళము కత్తిరించబడినది. ఘనము యొక్క అంచు. పొడవు 21 సెం.మీ. అయిన మిగిలిన చెక్కదిమ్మ యొక్క సంపూర్ణతల వైశాల్యము కనుగొనుము.
సాధన.
అర్ధగోళం వ్యాసము = 1 = 21 సెం.మీ. అనుకొనుము
అర్ధగోళం వ్యాసార్థం = [latex]\frac{l}{2}=\frac{21}{2}[/latex] సెం.మీ.
ఘనపు అంచు పొడవు = l = 21. సెం.మీ.
మిగిలిన చెక్కదిమ్మ సంపూర్ణతల వైశాల్యం =

ప్రశ్న 20.
6 సెం.మీ., 8 సెం.మీ. వ్యాసార్ధాలు కలిగిన రెండు లోహపు గోళాలను మరొక గోళముతో కలిపి కరిగించి ఒక పెద్ద గోళంగా తయారు చేయగా, దాని వ్యాసార్ధము 12 సెం.మీ. అయినది. అయిన మూడవ గోళము యొక్క వ్యాసార్ధము కనుగొనుము.
సాధన.
రెండు గోళాల వ్యాసార్ధాలు = r₁ = 6 సెం.మీ.
r₂ = 8 సెం.మీ.
గోళాల ఘనపరిమాణాలు = [latex]\frac{4}{3}[/latex] πr₁³, [latex]\frac{4}{3}[/latex] πr₂³
∴ పెద్ద గోళము యొక్క ఘనపరిమాణం = [latex]\frac{4}{3}[/latex] π(r₁³ + r₂³)
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × (6³ + 8³)
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 728 ………….. (1)
మూడవ గోళము వ్యాసార్ధము= ‘x’ సెం.మీ. అనుకొనిన మూడింటితో తయారైన గోళ ఘనపరిమాణం
= [latex]\frac{4}{3}[/latex] π(r₁³ + r₂³ + x³)
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] (728 + x³) …………………..(2)
పెద్ద గోళం వ్యాసార్ధము = 12 సెం.మీ.
పెద్ద గోళం ఘనపరిమాణం = [latex]\frac{4}{3}[/latex] π.12³
∴ (2) = (3)
[latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] (728 + x³) = [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 12³
⇒ 728 + x³ = 12³
⇒ x³ = 12³ – 728
= 1728 – 728
= 1000 సెం.మీ.
⇒ x = 10 సెం.మీ.

ప్రశ్న 21.
ఒక్కొక్కటి 216 ఘనపు సెం.మీ. ఘనపరిమాణము గల రెండు ఘనములు కలుపబడినవి అయిన ఏర్పడిన కొత్త దీర్ఘ ఘనము యొక్క సంపూర్ణ తల వైశాల్యము ఎంత ?
సాధన.
దత్తాంశం ప్రకారం, ఘనం యొక్క ఘనపరిమాణం V = a³ = 216 సెం.మీ³
∴ a³ = 6 × 6 × 6 = 6³
కావున, a = 6 సెం.మీ. –

రెండు ఘనములను కలిపినపుడు, దీర్ఘఘనము యొక్క పొడవు = 2a = 2 × 6 = 12 సెం.మీ.,
వెడల్పు = a = 6 సెం.మీ.,
ఎత్తు = a = 6 సెం.మీ.
∴ దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2(lb + bh + th)
= 2(12 × 6 + 6 × 6 + 12 × 6)
= 2(72 + 36 + 72) = 2 × 180
= 360 సెం.మీ.²
∴ కొత్తగా ఏర్పడిన దీర్ఘ ఘనము యొక్క సంపూర్ణతల వైశాల్యం 360 సెం.మీ.²

These AP 8th Class Biology Important Questions 8th Lesson మొక్కల నుండి ఆహారోత్పత్తి will help students prepare well for the exams.

AP Board 8th Class Biology 8th Lesson Important Questions and Answers మొక్కల నుండి ఆహారోత్పత్తి

ప్రశ్న 1.
రైతులు నాట్లు వేసి పండించే పంటలకు రెండు ఉదాహరణలు రాయండి.
జవాబు:
వరి, గోధుమ, మిరప

ప్రశ్న 2.
ఖరీఫ్, రబీ అంటే ఏమిటి ? ఈ కాలంలో పండే పంటలకు ఉదాహరణలు రాయండి.
జవాబు:

1. వర్షాకాలంలో పండే పంటల్ని ఖరీఫ్ పంటలు అంటారు.
2. ఖరీఫ్ పంట కాలం జూన్ – అక్టోబర్.
3. ఖరీఫ్ లో పండించే పంటలు వరి, పసుపు, చెరుకు, జొన్న
4. శీతాకాలంలో పండే పంటల్ని రబీ రబీ పంటలు అంటారు. రబీ పంటకాలం .అక్టోబరు, మార్చి.
5. రబీలో పండించే పంటలు గోధుమ వరి, జీలకర్ర, ధనియాలు, ఆవాలు.

ప్రశ్న 3.
క్రింది చిత్రం చూడండి. అడిగిన ప్రశ్నలకు సమాధానం రాయండి.

ఎ) ఇది ఏరకమైన ఎరువు ?
బి) ఇందులో ఉన్న రసాయన పదార్థాలు ఏవి ?
సి) 20-5-10 దేనిని సూచిస్తుంది.
డి) ఇలాంటి ఎరువులు వాడడం వల్ల లాభమా ? నష్టమా ? ఎందుకు ?
జవాబు:
ఎ) రసాయనిక ఎరువు
బి) నైట్రోజన్ (N) ఫాస్పరస్ (P) పోటాషియం (K)
సి) 20 – నైట్రోజన్ శాతం 5 – ఫాస్పరస్ శాతం – 10 – పొటాషియం శాతం
డి) ఇలా ఈ రసాయనిక ఎరువులను అధిక మొత్తాలలో వాడటం వలన నేల ఆరోగ్యం తగ్గిపోతుంది.

ప్రశ్న 4.
కింది పట్టికను చదివి ప్రశ్నలకు సమాధానం రాయండి.

1. మొక్కలలో శిలీంధ్రాల ద్వారా వచ్చే వ్యాధులేవి ?
జవాబు:
చెరకు ఎర్రకుళ్ళు తెగులు, వేరుశనగ టిక్కా తెగులు.

2. ఏయే వ్యాధులు గాలి ద్వారా వ్యాపిస్తాయి ?
జవాబు:
ఎర్ర కుళ్ళు తెగులు, సిట్రస్ కాంకర్, వేరుశగన టిక్కా తెగులు.

3. వేరుశనగలో తిక్కా తెగులుకు కారణమైన సూక్ష్మజీవి ఏది ?
జవాబు:
శిలీంధ్రం

4. వైరస్టు దేని ద్వారా పొగాకులో మొజాయిక్ వ్యాధిని కలిగిస్తాయి ?
జవాబు:
కీటకాల ద్వారా

5. స్ప్రింక్లర్ మరియు బిందు సేద్యం మధ్య పోలిక ఏమి ?
జవాబు:
స్ప్రింకర్లు మరియు బిందు సేద్య పద్ధతులను నీరు తక్కువగా లభించే ప్రాంతాలలో పంటలను పండించడానికి . వినియోగించే సూక్ష్మ సేద్య పద్ధతులు.

1 మార్కు ప్రశ్నలు

ప్రశ్న 1.
రామయ్య తన పొలాన్ని చదునుగా దున్నాడు. సోమయ్య పొలం హెచ్చుతగ్గులు ఉంది. ఎవరు అధిక దిగుబడి సాధిస్తారు? ఎందుకు ?
జవాబు:
రామయ్య ఎక్కువ దిగుబడి సాధిస్తాడు. కారణం నేలను చదును చేయడం వలన పొలంలో నీరు అన్నివైపులకు సమానంగా ప్రసరించును. పొలంలో వేసిన పశువుల ఎరువు కూడా సమానంగా నేలలో కలిసి అన్ని మొక్కలకు అందును. విత్తనాలు వేయుటకు లేదా నారు మొక్కలు నాటడానికి వీలుగా ఉండును.

ప్రశ్న 2.
విత్తనాలు నేలలో విత్తే ముందర శిలీంధ్ర నాశకాల వంటి రసాయనిక పదార్థాలతో శుద్ధి చేస్తారు. ఎందుకు ?
జవాబు:
విత్తనాలు నేలలో విత్తే ముందర శిలీంధ్ర నాశకాల వంటి రసాయనిక పదార్థాలతో శుద్ధి చేస్తారు. ఎందుకంటే నేలలో ‘ఉన్న ఏవైనా శిలీంధ్రాలు, ఇతర సూక్ష్మజీవుల నుండి విత్తనాలను రక్షించుకొనుటకు.

ప్రశ్న 3.
వేసవి దుక్కులు అంటే ఏమిటి ?
జవాబు:
రైతులు వేసవికాలంలోనే తమ పొలాలను దున్నుతారు. వీటిని వేసవి దుక్కులు అంటారు.

ప్రశ్న 4.
మన దేశంలోని అన్ని ప్రాంతాలలో పండే పంటలు ఏవి ?
జవాబు:
వరి, గోధుమ, మొక్కజొన్న, పప్పు ధాన్యాలు, ప్రత్తి.

ప్రశ్న 5.
కొన్ని పంటలను అన్ని ప్రాంతాలలోనూ ఎందుకని పండించగలుగుతున్నారు ?
జవాబు:
సారవంతమైన భూమి, నీరు లభ్యత వలన.

ప్రశ్న 6.
గోధుమ పంటను నవంబర్ లో సాగుచేస్తే ఏమవుతుంది ?
జవాబు:
గోధుమ పంటను నవంబర్ లో సాగుచేస్తే పంట దిగుబడి ఎక్కువగా వస్తుంది. కారణం ఫిబ్రవరిలో రాత్రి సమయం 12 1/2 గంటలు ఉండి బాగా పుష్పిస్తాయి.

ప్రశ్న 7.
ఎందుకు కొన్ని విత్తనాలు నీళ్ళ పై తేలుతాయి ?
జవాబు:
కొన్ని విత్తనాలు నీళ్ళపై తేలుతాయి. కారణం అవి పుచ్చు విత్తనాలు అయి ఉండటం వలన విత్తనం లోపల ఖాళీగా ఉండి నీటికన్న తక్కువ సాంద్రత కలిగి ఉంటాయి. అందుకని నీటిపై తేలుతాయి.

ప్రశ్న 8.
తేలిన విత్తనాలను ఎందుకు తీసివేయాలి ?
జవాబు:
తేలిన విత్తనాలకు మొలకెత్తే సామర్థ్యం ఉండదు కాబట్టి వాటిని తీసివేయాలి.

ప్రశ్న 9.
విత్తనాలను ఒక రోజంతా నీళ్ళలో ఎందుకు నానబెట్టాలి ?
జవాబు:
విత్తనాలను ఒక రోజంతా నీళ్ళలో నానబెట్టడం వలన విత్తనం తేమగా అయ్యి విత్తనాలకు అంకురించే శక్తి వస్తుంది.

ప్రశ్న 10.
విత్తనాలను నేలలో విత్తిన తరువాత మట్టితో ఎందుకు కప్పుతారు ?
జవాబు:
విత్తనాలను నేలలో విత్తిన తరువాత మట్టితో కప్పుటకు కారణాలు మట్టి నుండి వాటికి కావలసిన తేమను, వేడిమిని పొందుటకు మరియు గుల్లగా ఉన్న నేల నుండి గాలిని తీసుకొనుటకు. మట్టిలో విత్తిన తర్వాత కప్పకపోతే పక్షులు, ఇతర జంతువులు ఆ విత్తనాలను తినేస్తాయి.

ప్రశ్న 11.
జపాన్లో అధిక దిగుబడి సాధించడానికి గల కారణాలేవి ?
జవాబు:
జపాన్ వ్యవసాయ రంగంలో ఆధునిక పద్ధతులు ఉపయోగించటం, జపాన్ అత్యధిక దిగుబడి నిచ్చే వరి విత్తనాలు ఉపయోగించటం.

ప్రశ్న 12.
భారతదేశంలో తక్కువ దిగుబడి సాధించడానికి గల కారణాలేవి ?
జవాబు:
భారతదేశం వ్యవసాయ రంగంలో ప్రాచీన పద్ధతులు ఉపయోగించటం, వ్యవసాయంలోనికి చదువుకున్న వాళ్ళు రాకపోవటం.

ప్రశ్న 13.
మూడవ పంట అన్ని ప్రాంతాలలో పండించకపోవడానికి కారణాలు ఏమిటి?
జవాబు:
నీటి పారుదల వసతి లేకపోవడం. నేల సారాన్ని కోల్పోవడం.

ప్రశ్న 14.
వరి పండించే పొలాన్ని చిన్న చిన్న మడులుగా ఎందుకు చేస్తారు ?
జవాబు:
పంటకు నీరు అందించుట సులభంగా ఉంటుంది. కాబట్టి వరి పండించే పొలాన్ని చిన్న చిన్న మడులుగా చేస్తారు.

ప్రశ్న 15.
వరిని ఎలా పండిస్తారు ?
జవాబు:
వరిని నారుపోసి, నాట్లు వేసి చిన్న చిన్న మడులలో పండిస్తారు.

ప్రశ్న 16.
ప్రస్తుతం సంప్రదాయంగా సాగుచేస్తున్న విత్తనాలు కనుమరుగవుతున్నాయి ? ఇలా ఎందుకు జరుగుతోంది ఆలోచించండి.
జవాబు:
ప్రస్తుతం సంప్రదాయంగా సాగుచేస్తున్న విత్తనాలు కనుమరుగవుతున్నాయి. ఎందుకు ఇలా జరుగుతోంది అంటే వాటి స్థానాన్ని సంకరణ జాతి విత్తనాలు ఆక్రమించటం వలన.

ప్రశ్న 17.
నారు నాటడం ద్వారా ఇంకా ఏ ఏ పంటలు పండిస్తారు?
జవాబు:
మిరప, వంగ, టమోటా మొదలైన పంటలు నారు నాటడం ద్వారా పండిస్తారు.

ప్రశ్న 18.
ఎందుకు నారు మొక్కలను దూరం దూరంగా నాటుతారు ?
జవాబు:
నారు మొక్కలు దూరం దూరంగా నాటుటకు కారణం అవి పెరిగి పెద్దగా అయిన తర్వాత స్థలం కోసం, నీటి కోసం, ఆహార పదార్థాల కోసం పోటీ లేకుండా ఉండుటకు.

ప్రశ్న 19.
అన్ని రకాల పంటలను నారు మొక్కల్లాగానే పీకి మళ్ళీ నాటుతారా ? అలా ఎందుకు చేయరు ?
జవాబు:
అన్ని రకాల పంటలను నారు మొక్కల్లాగా మళ్ళీ పీకి నాటరు. కారణం వాటి విత్తనాలు పెద్దవిగా ఉండటం.

ప్రశ్న 20.
వ్యాధి సోకిన పంటలోని మొక్కలను రైతు ఏం చేస్తాడు ?
జవాబు:
వ్యాధి సోకిన పంటలోని మొక్కల ఆకులు, అవసరం అనుకొంటే మొక్కలను రైతు తొలగిస్తాడు. అవి అన్నీ ఒకచోట వేసి కాలుస్తాడు.

ప్రశ్న 21.
కలుపు మొక్కలను ఎందుకు తొలగించాలి ?
జవాబు:
కలుపు మొక్కలు పోషక పదార్థాలు, నీరు, వెలుతురు కోసం పంట మొక్కలతో పోటీపడతాయి. దీనివల్ల సాగు మొక్కలు పెరగవు. అందుకే కలుపు మొక్కలు తొలగించాలి.

లక్ష్యాత్మక నియోజనము

ప్రశ్న 1.
ఈ కింది వాటిలో మొక్కలు పుష్పించడానికి రాత్రికాల – సమయానికి ప్రభావం ఏమాత్రం ఉండదు.
ఎ) వేరుశనగ
బి) పత్తి
సి) సోయా చిక్కుడు
డి) వరి
జవాబు:
సి) సోయా చిక్కుడు

ప్రశ్న 2.
నాగలితో నేలను దున్నినపుడు ఏ ఆకారంలో చాళ్ళు ఏర్పడతాయి?
ఎ) T
బి) S
సి) V
డి) W
జవాబు:
సి) V

ప్రశ్న 3.
విత్తనాలను ఎప్పుడు రసాయనిక పదార్థాలతో శుద్ధి చేస్తారు?
ఎ) ఏర్పడినప్పుడు
బి) నాటే ముందు
సి) దాచే ముందు
డి) కోతల ముందు
జవాబు:
డి) కోతల ముందు

ప్రశ్న 4.
వేరుశనగలో వచ్చే శిలీంధ్ర వ్యాధి
ఎ) తుప్పు తెగులు
బి) టిక్కా తెగులు
సి) ఏర్రకుళ్ళు తెగులు
డి) అగ్గి తెగులు
జవాబు:
బి) టిక్కా తెగులు

ప్రశ్న 5.
కలుపు మొక్కలను ద్విదళ బీజాలలో నిర్మూలించుటకు ఉపయోగించే రసాయనం పేరు
ఎ) నాప్తలీన్ ఎసిటికామ్లం
బి) ఇండోల్ బ్యూటరిక్ ఆమ్లం
సి) ఎసిటికామ్లం
డి) 2,4 – D
జవాబు:
డి) 2,4 – D

ప్రశ్న 6.
పంట నుండి గింజలను సేకరించుటను ఏమి అంటారు ?
ఎ) పంటకోతలు
బి) పంట నూర్పిళ్ళు
సి) నీటి పారుదల
డి) కలుపు తీయుట
జవాబు:
బి) పంట నూర్పిళ్ళు

ప్రశ్న 7.
మొదటి వరి పంట రైతులు ఎవరికి పెడతారు ?
ఎ) పిచ్చుకలు
బి) గ్రద్దలు
సి) కాకులు
డి) కోళ్ళు
జవాబు:
ఎ) పిచ్చుకలు

ప్రశ్న 8.
పంట అనగా
ఎ) మనకు ఉపయోగపడే మొక్కలను అధిక సంఖ్యలో పెంచడం
బి) ఆహారంగా ఉపయోగపడే మొక్కలను అధిక సంఖ్యలో పెంచడం
సి) తోటలు పెంచడం
డి) ధాన్యాన్ని పండించడం
జవాబు:
ఎ) మనకు ఉపయోగపడే మొక్కలను అధిక సంఖ్యలో పెంచడం

ప్రశ్న 9.
దీర్ఘకాలిక పంటలు పండించడానికి ఎన్ని రోజుల కన్నా ఎక్కువ సమయం పడుతుంది ?
ఎ) 90 రోజులు
బి) 180 రోజులు
సి) 270 రోజులు
డి) 360 రోజులు
జవాబు:
బి) 180 రోజులు

ప్రశ్న 10.
క్రింది వానిలో దీర్ఘ కాలిక పంట కానిది
ఎ) జొన్న
బి) కందులు
సి) మినుములు
డి) పైవేవీ కావు
జవాబు:
సి) మినుములు

ప్రశ్న 11.
క్రింది వానిలో స్వల్పకాలిక పంట ఏది?
ఎ) పెసలు
బి) మినుములు
సి) ఎ మరియు బి
డి) పైవేవీ కావు
జవాబు:
సి) ఎ మరియు బి

ప్రశ్న 12.
స్వల్పకాలిక పంటలు పండటానికి ఇంతకన్నా తక్కువ సమయం పడుతుంది.
ఎ) 60 రోజులు
బి) 100 రోజులు
సి) 120 రోజులు
డి) 150 రోజులు
జవాబు:
బి) 100 రోజులు

ప్రశ్న 13.
అరబిక్ భాషలో ఖరీఫ్ అనగా
ఎ) ఎండ
బి) గాలి
సి) వర్షం
డి) చలి
జవాబు:
సి) వర్షం

ప్రశ్న 14.
ఈ క్రింది వానిలో ఖరీఫ్ కాలం
ఎ) జూన్ నుండి అక్టోబర్
బి) అక్టోబర్ నుండి మార్చి
సి) ఆగస్టు నుండి అక్టోబర్
డి) ఆగస్టు నుండి మార్చి
జవాబు:
ఎ) జూన్ నుండి అక్టోబర్

ప్రశ్న 15.
ఈ క్రింది వానిలో ఖరీఫ్ పంట కానిది
ఎ) శనగలు
బి) పసుపు
సి) చెణకు
ది) జొన్న
జవాబు:
ఎ) శనగలు

ప్రశ్న 16.
రబీ కాలం అనగా
ఎ) జూన్ నుండి అక్టోబర్
బి) అక్టోబర్ నుండి మార్చి
సి) ఆగస్టు నుండి అక్టోబర్
డి) ఆగస్టు నుండి మార్చి
జవాబు:
బి) అక్టోబర్ నుండి మార్చి

ప్రశ్న 17.
అరబిక్ భాషలో రబీ అనగా
ఎ) వర్షం
బి) ఎండ
సి) గాలి
డి) చలి
జవాబు:
డి) చలి

ప్రశ్న 18.
ఈ క్రింది వానిలో రబీ పంట కానిది
ఎ) ఆవాలు
బి) ధనియాలు
సి) జీలకర్ర
డి) మీరపు
జవాబు:
డి) మీరపు

ప్రశ్న 19.
గోధుమ పంట పండే కాలము
ఎ) ఖరీఫ్
బి) రబీ
సి) వర్షాకాలం
డి) చలికాలం
జవాబు:
బి) రబీ

ప్రశ్న 20.
గోధుమ పంట బాగా పందాలంటే వాతావరణం ఇలా ఉండాలి.
ఎ) వేడి
బి) తేమ
సి) ఆర్ధత
డి) చల్లదనం
జవాబు:
ఎ) వేడి

ప్రశ్న 21.
విశ్వధాన్యపు పంట అని దేనినంటారు ?
ఎ) వరి
బి) గోధుమ
సి) చెఱకు
డి) మొక్కజొన్న
జవాబు:
ఎ) వరి

ప్రశ్న 22.
ప్రపంచంలో అధిక విస్తీర్ణంలో వరిని పండించే దేశం
ఎ) చైనా
బి) జపాన్
సి) భారత్
డి) అమెరికా
జవాబు:
సి) భారత్

ప్రశ్న 23.
ఒక హెక్టారుకు వరి దిగుబడి అధికంగా ఉన్న దేశం
ఎ) అమెరికా
బి) చైనా
సి) జపాన్
డి) భారత్
జవాబు:
సి) జపాన్

ప్రశ్న 24.
ఏరువాక పండుగలో
ఎ) వ్యవసాయ పనులు మొదలు పెడతారు.
బి) నారు పోస్తారు.
సి) నాట్లు వేస్తారు.
డి) పంట నూర్పిళ్ళు చేస్తారు.
జవాబు:
ఎ) వ్యవసాయ పనులు మొదలు పెడతారు.

ప్రశ్న 25.
అక్షయ తృతీయ పండుగతో
ఎ) వ్యవసాయ పనులు మొదలు పెడతారు.
బి) నాట్లు వేస్తారు.
సి) నీరు పెట్టి ఎరువులు వేస్తారు.
డి) పంట నూర్పిళ్ళు చేస్తారు.
జవాబు:
బి) నాట్లు వేస్తారు.

ప్రశ్న 26.
పంట నూర్పిళ్ళప్పుడు వచ్చే పందుగ
ఎ) ఓనం
బి) సంక్రాంతి
సి) ఎ మరియు బి
డి) పైవేవీ కావు
జవాబు:
సి) ఎ మరియు బి

ప్రశ్న 27.
కలుపు మొక్కలను తొలగించటానికి ఉపయోగపడేది
ఎ) నాగలిబి
బి) మల్లగొర్రు
సి) చదును పలక
డి) గుంటక
జవాబు:
బి) మల్లగొర్రు

ప్రశ్న 28.
నేలను చదును చేయుటకు దీనిని ఉపయోగిస్తారు.
ఎ) నాగలి
బి) మడ్ల గొర్రు
సి) చదును పలక
డి) పార
జవాబు:
సి) చదును పలక

ప్రశ్న 29.
మంచి విత్తనాలు యిలా ఉంటాయి.
ఎ) తేలికగా ముడుతలతో
బి) బరువుగా ముడుతలతో
సి) తేలికగా గుండ్రంగా
డి) బరువుగా గుండ్రంగా
జవాబు:
డి) బరువుగా గుండ్రంగా

ప్రశ్న 30.
ఆసియాలో పండించే వరి రకం
ఎ) ఒరైజా సటైవా
బి) ఒరైజా గ్లజెర్రిమా
సి) ఒరైజా గ్లుమోపాట్యులా
డి) ఒరైజా ఒరైజా
జవాబు:
ఎ) ఒరైజా సటైవా

ప్రశ్న 31.
అమృతసారి, బంగారుతీగ, కొల్లేటి కుసుమ, పొట్టి బాసంగి ఏ సాంప్రదాయ పంట రకాలు ?
ఎ) వరి
బి) గోధుమ
సి) జొన్న
డి) వేరుశనగ
జవాబు:
ఎ) వరి

ప్రశ్న 32.
సోనా రకం బియ్యం ఈ జిల్లాలో ఎక్కువగా పండుతాయి.
ఎ) కడప
బి) కర్నూలు
సి) నెల్లూరు
బి) గుంటూరు
జవాబు:
బి) కర్నూలు

ప్రశ్న 33.
నెల్లూరు జిల్లాలో పండే వరి రకం
ఎ) సోనా
బి) అమృతసారి
సి) మొలగొలుకులు
డి) పొట్టి బాసంగి
జవాబు:
సి) మొలగొలుకులు

ప్రశ్న 34.
రైతులకు మంచి విత్తనాలు అందించే సంస్థ
ఎ) ICRISAT
బి) NSDC
సి) IRRI
డి) NSRI
జవాబు:
బి) NSDC

ప్రశ్న 35.
శ్రీ వరి సాగులో SRI అనగా
ఎ) సిస్టమ్ ఆఫ్ రైస్ ఇంటెన్సిఫికేషన్
బి) సిస్టమ్ ఆఫ్ రైస్ ఇంటిగ్రిటి
సి) సీల్డింగ్ ఆఫ్ రైస్ ఇంటెన్సిఫికేషన్
డి) సీడ్లింగ్ ఆఫ్ రోస్ ఇంటెన్సిఫికేషన్
జవాబు:
ఎ) సిస్టమ్ ఆఫ్ రైస్ ఇంటెన్సిఫికేషన్

ప్రశ్న 36.
టిక్కా తెగులు ఈ పంటలో వస్తుంది.
ఎ) వరి
బి) చెటుకు
సి) నిమ్మ
డి) వేరుశనగ
జవాబు:
డి) వేరుశనగ

ప్రశ్న 37.
దైథేన్ ఎమ్ – 45 అనేది ఒక
ఎ) ఎరువు
బి) కలుపునాశిని
సి) కీటకనాశిని
డి) ఫంగి సైడ్
జవాబు:
సి) కీటకనాశిని

ప్రశ్న 38.
క్రిమి సంహారక మందు తయారుచేయటానికి ఉపయోగపడే మొక్క
ఎ) వేప
బి) పొగాకు
సి) చామంతి
డి) పైవన్నీ
జవాబు:
డి) పైవన్నీ

ప్రశ్న 39.
D.D.T ని విస్తరించగా
ఎ) డై క్లోరో డై ఫినైల్ టై క్లోరో ఈథేన్
బి) డై ఫినైల్ డై క్లోరో టై క్లోరో ఈథేన్
సి) డైక్లోరో డై ఫినైల్ టై క్లోరో మీథేన్
డి) డై ఫినైల్ డై క్లోరో టై క్లోరో మీథేన్
జవాబు:
ఎ) డై క్లోరో డై ఫినైల్ టై క్లోరో ఈథేన్

ప్రశ్న 40.
సైలెంట్ స్ప్రింగ్ పుస్తకాన్ని రచించినది
ఎ) స్వామినాథన్
బి) అమర్త్యసేన్
సి) రేచల్ కార్సన్
డి) అరుంధతీ రాయ్
జవాబు:
సి) రేచల్ కార్సన్

ప్రశ్న 41.
ఏరసాయనిక పదార్థం ఆహారపు గొలుసులోకి ప్రవేశించి పక్షుల గ్రుడ్లు పగిలిపోటానికి కారణమవుతుంది.
ఎ) D.D.T
బి) B.H.C
సి) ఎండ్రిన్
డి) ఎండోసల్ఫాన్
జవాబు:
ఎ) D.D.T

ప్రశ్న 42.
ఈ క్రింది వానిలో స్థూల పోషకం కానిది ఏది ?
ఎ) నత్రజని
బి) కాల్షియం
సి) పొటాషియం
డి) భాస్వరం
జవాబు:
బి) కాల్షియం

ప్రశ్న 43.
నీటిని మొక్కలకు పొదుపుగా అందించే పద్దతి
ఎ) స్ప్రింక్లర్
బి) బిందు సేద్యం
సి) పై రెండూ
డి) పైవేవీ కావు
జవాబు:
సి) పై రెండూ

ప్రశ్న 44.
స్ప్రింక్లర్ ఈ సూత్రంపై ఆధారపడి పని చేస్తుంది.
ఎ) గాలిపీడనం
బి) నీటి పీడనం
సి) విద్యుత్
డి) ప్రవాహవేగం
జవాబు:
బి) నీటి పీడనం

ప్రశ్న 45.
మనదేశానికి అమెరికా నుండి గోధుమలతో దిగుమతి చేయబడిన కలుపు మొక్క
ఎ) వరి ఎల్లగడ్డి
బి) వయ్యారిభామ
సి) గోలగుండి
డి) గడ్డిచామంతి
జవాబు:
బి) వయ్యారిభామ

ప్రశ్న 46.
2, 4 Dఒక
ఎ) ఏకదళబీజ కలుపునాశిని
బి) ద్విదళబీజ కలుపునాశిని
సి) కీటకనాశిని
డి) శిలీంధ్రనాశిని
జవాబు:
బి) ద్విదళబీజ కలుపునాశిని

ప్రశ్న 47.
తొందరగా చెడిపోయి రంగు మారిపోయే పంట ఉత్పత్తులను ఎక్కడ భద్రపరుస్తారు ?
ఎ) గారెలు
బి) గోదాములు
సి) శీతల గిడ్డంగులు
డి) భూమిలోపాతర
జవాబు:
సి) శీతల గిడ్డంగులు

ప్రశ్న 48.
రత్నబాబు, నీటి కొరత వున్న తన పొలంలో పంట పండించాలని అనుకున్నాడు. కింది వాటిలో ఏ పద్ధతిని ఉత్తమమైన పద్ధతిగా అతనికి సూచించవచ్చు.
(A) చాళ్ళ ద్వారా నీటి పారుదల
(B) మడుల ద్వారా నీటి పారుదల
(C) బిందు సేద్యం
(D) పంపునీరు
జవాబు:
(C) బిందు సేద్యం

ప్రశ్న 49.
కింది వాటిలో తక్కువ పగలు (లేదా) ఎక్కువ రాత్రి కాలపు పంట
(A) సోయాబీన్
(B) జొన్న
(C) బఠాణి
(D) గోధుమ
జవాబు:
(D) గోధుమ

ప్రశ్న 50.
ఖరీఫ్ ఈ మధ్య కాలంలో పెంచబడే పంట
(A) డిసెంబర్ – ఏప్రిల్
(B) నవంబర్ – మార్చి
(C) అక్టోబర్ – ఏప్రిల్
(D) జూన్ – నవంబర్
జవాబు:
(D) జూన్ – నవంబర్

ప్రశ్న 51.
సరైన క్రమంలో అమర్చండి
1. ఎరువులు అందించడం
2. నేలను సిద్ధం చేయడం
3. నీటి పారుదల సౌకర్యం కల్పించడం
4. విత్తనాలు నాటడం
(A) 1, 2, 3, 4
(B) 2, 4, 1, 3
(C) 3, 1, 4, 2
(D) 3, 1, 2, 4
జవాబు:
(B) 2, 4, 1, 3

ప్రశ్న 52.
వ్యవసాయంలో యంత్రాలు వాడటం వలన జరిగే పరిణామం
(A) సమయం వృధా అవుతుంది
(B) ధనం వృధా అవుతుంది
(C) శ్రమ అధికమవుతుంది.
(D) కూలీలు పని కోల్పోతారు.
జవాబు:
(D) కూలీలు పని కోల్పోతారు.

ప్రశ్న 53.
ప్రస్తుతం భారతదేశంలో సాగుబడిలో ఉండే వరి వంగదాల సంఖ్య
(A) 1 డజను
(B) 2 డజనులు
(C) 3 డజనులు
(D) 4 డజనులు
జవాబు:
(A) 1 డజను

ప్రశ్న 54.
బెల్లంలో ఉండే మూలకం
(A) కాల్షియం
(B) ఇనుము
(C) హైడ్రోజన్
(D) క్లోరిన్
జవాబు:
(B) ఇనుము

ప్రశ్న 55.
కృత్రిమ ఎరువు కానిది
(A) కుళ్ళిన వ్యర్థాలు
(B) యూరియా
(C) అమ్మోనియం ఫాస్పేట్
(D) అమ్మోనియం నైట్రేట్
జవాబు:
(A) కుళ్ళిన వ్యర్థాలు

ప్రశ్న 56.
కింది వాక్యాలను చదవండి.
P. అఫిడ్స్ మరియు తెల్లదోమలు మొక్కలనుండి రసాలను పీల్చడమేకాక మొక్కలకు వైరస్ వ్యాధులను కలుగజేస్తాయి.
Q. రెక్కలు లేని దక్కను జాతి గొల్లభామను రబీ సీజన్లోనే చూడగలము. పై వాటిలో సరైనవి
(A) P, Q రెండూ సరైనవి
(B) P,Q రెండూ సరికాదు
(C) P సరైనది, Q సరైనది కాదు
(D) P సరైనది కాదు. Q సరైనది
జవాబు:
(A) P, Q రెండూ సరైనవి

ప్రశ్న 57.
నేలను దున్నడం వల్ల కలిగే ప్రయోజనాలు
(A) వర్షం పడినప్పుడు నీరు బాగా శోషించబడుతుంది
(B) నేలలోకి గాలి బాగా ప్రసరిస్తుంది.
(C) నేలలోని అపాయకరమైన సూక్ష్మజీవులు చనిపోతాయి
(D) పైవన్నీ
జవాబు:
(D) పైవన్నీ

ప్రశ్న 58.
కింది వాక్యాలను చదవండి.
(A) : స్ప్రింక్లర్ ఒక ఆధునిక నీటి పారుదల పద్ధతి
(R) : నీటి ఎద్దడి గల ప్రాంతాలలో ‘బిందు సేద్యం’ అనువైన పద్ధతి
(A) A, R రెండూ సరైనవి. R, Aకి సరైన వివరణ
(B) A, Rలు రెండూ సరైనవి, R, Aకి సరైన వివరణ కాదు
(C) A సరికాదు. R సరియైనది.
(D) A, Rలు రెండూ సరికావు
జవాబు:
(B) A, Rలు రెండూ సరైనవి, R, Aకి సరైన వివరణ కాదు

These AP 10th Class Maths Chapter Wise Important Questions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు will help students prepare well for the exams.

AP Board 10th Class Maths 9th Lesson Important Questions and Answers వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు

ప్రశ్న 1.
క్రింది పటంలో గల వృత్తానికి a, b, భాగాలను ఏమని పిలుస్తారు ?
సాధన.

a ని అల్ప వృత్తఖండము మరియు b ని అధిక వృత్తఖండం అని పిలుస్తారు.

ప్రశ్న 2.
7 సెం.మీ. వ్యాసార్ధముగా కల్గిన వృత్త కేంద్రం నుండి 25 సెం.మీ. దూరంలో ఉన్న బిందువు నుండి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనండి.
సాధన.
దత్తాంశము OA = 25 సెం.మీ.,
OB = r = 7 సెం.మీ.
∆AOB లో ∠B = 90°

∴ OA² = OB² + AB²
⇒ AB² = OA² – OB² = 25² – 7²
⇒ AB = √(25² – 7²)
= √(625 – 49)
= √576 = 24 సెం.మీ.

ప్రశ్న 3.
4 సెం.మీ. వ్యాసార్ధం గల ఒక వృత్త కేంద్రం నుండి 5 సెం.మీ. దూరంలో ఉన్న ఒక బిందువు నుండి ఆ వృత్తానికి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనుము.
సాధన.

∆OAB అనునది లంబకోణ త్రిభుజము.
OA² = OB² + AB²
5² = OB² + 4²
⇒ OB² = 25 – 16 = 9
∴ OB = √9 = 3 సెం.మీ.

ప్రశ్న 4.
ఇవ్వబడిన పటంలో షేడ్ చేసిన ప్రాంత వైశాల్యం కనుగొనండి.

సాధన.
షేడ్ చేసిన ప్రాంత వైశాల్యం = అర్ధవృత్త వైశాల్యం – త్రిభుజ వైశాల్యం
= [latex]\frac{\pi \mathrm{r}^{2}}{2}[/latex] – [latex]\frac{1}{2}[/latex]bh
= [latex]\frac{\frac{22}{7} \times 7 \times 7}{2}[/latex] – [latex]\frac{1}{2}[/latex] × 14 × 6
= 11 × 7 – 7 × 6
= 77 – 42 = 35 చ.సెం.మీ.

ప్రశ్న 5.
7 సెం.మీ. వృత్త వ్యాసార్ధము మరియు కేంద్రం వద్ద కోణం 60° గా గల వృత్త సెక్టారు యొక్క వైశాల్యమును కనుగొనండి.
సాధన.
వ్యాసార్ధం = 7 సెం.మీ., కేంద్రం వద్ద కోణం = 60°
సెక్టారు యొక్క వైశాల్యము = [latex]\frac{x}{360}[/latex] × πr
= [latex]\frac{60 \times \frac{22}{7} \times 7 \times 7}{360}=\frac{154}{6}[/latex]
= 25.66 సెం.మీ.²

ప్రశ్న 6.
3 సెం.మీ. వ్యాసార్ధముతో వృత్తాన్ని గీచి, వృత్త పరిధిపై బిందువు ‘P’ ను గుర్తించి దానిగుండా పోయే స్పర్శరేఖను గీయండి.
సాధన.
నిర్మాణ క్రమము : –

1) “O” కేంద్రముగా 3 సెం.మీ. వ్యాసార్ధముతో వృత్తమును గీచితిని. వృత్త పరిధిపై ‘P’ బిందువును గుర్తించి [latex]\overline{\mathrm{OP}}[/latex]ని గీచితిని.
2) [latex]\overline{\mathrm{OP}}[/latex] కు లంబంగా [latex]\overline{\mathrm{XY}}[/latex] ను నిర్మించితిని.
∴ [latex]\overline{\mathrm{XY}} \perp \overline{\mathrm{OP}}[/latex]
3) [latex]\overline{\mathrm{XY}}[/latex] వృత్తానికి ‘P’ గుండా పోయే స్పర్శరేఖ అవుతుంది.

ప్రశ్న 7.
3 సెం.మీ. వ్యాసార్థం గల వృత్తాన్ని గీయండి. దాని కేంద్రం నుండి 5 సెం.మీ. దూరంలో ‘P’ అనే బిందువును గుర్తించి, P నుండి వృత్తానికి 2 స్పర్శరేఖలు గీయండి.
సాధన.
నిర్మాణక్రమం : .
i) 3 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీయుము.

ii) 0 నుండి 5 సెం.మీ. దూరంలో P గుర్తించి, OP ని కలుపుము.
iii) OPను లంబ సమద్వి ఖండన చేయగా అది OP ని Mవద్ద ఖండించినచో M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీయుము.
iv) వృత్తాల ఖండన బిందువుల నుండి స్పర్శరేఖలు గీయుము.

ప్రశ్న 8.
4 సెం.మీ. వ్యాసార్ధముతో ఒక వృత్తాన్ని గీయండి. కేంద్రము నుండి 7.5 సెం.మీ. దూరములో గల బిందువు నుండి ఒక జత, స్పర్శరేఖలు గీయండి.
సాధన.
నిర్మాణ క్రమము :

1) 0 కేంద్రంగా 4 సెం.మీ. వ్యాసార్ధముతో వృత్తంను గీయుము.
2) 0 కేంద్రంగా 7.5 సెం.మీ. దూరంలో P బిందువును గుర్తించి, OP ని కలుపుము.
3) OP ను లంబ సమద్విఖండన చేసి M ను గుర్తించి
M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీయుము.
4) P నుండి వృత్తాల ఖండన బిందువులకు స్పర్శరేఖలు CPA మరియు PB గీయుము.

ప్రశ్న 9.
5 సెం.మీ. వ్యాసార్థము గల వృత్తమును గీచి, వృత్త కేంద్రము నుండి 8 సెం.మీ. దూరములో గల బిందువు నుండి ఒక జత స్పర్శరేఖలను నిర్మించుము.
సాధన.

నిర్మాణము :
1) ‘O’ కేంద్రముగా 5 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీచితిని.
2) ‘0’ నుండి 8 సెం.మీ. దూరంలో ‘P’ గుర్తించి, OP ని కలిపితిని.
3) OP ను లంబ సమద్విఖండన చేయగా అది OPని ‘M’ వద్ద ఖండించినది. M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీచితిని.
4) P నుండి వృత్తాల ఖండన బిందువులైన T, , T, లకు స్పర్శరేఖలు PT, మరియు PT, లను గీచితిని.

ప్రశ్న 10.
4 సెం.మీ. వ్యాసార్ధంతో ఒక వృత్తాన్ని గీయండి. కేంద్రం నుండి 6 సెం.మీ. దూరములో గల బిందువు వద్ద ఖండించుకొనునట్లు ఒక జత స్పర్శరేఖలను గీయండి. .
సాధన.

నిర్మాణ క్రమము :
i) 0 కేంద్రముగా 4 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీచితిని.
ii) 0 నుండి 6.సెం.మీ. దూరంలో P గుర్తించి, OP కలిపితిని.
iii)OPను లంబ సమద్విఖండన చేయగా అది OPని M వద్ద ఖండించును. M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీచితిని.
iv)వృత్తాల ఖండన బిందువుల నుండి స్పర్శరేఖలు గీచితిని.

ప్రశ్న 11.
కింది పటం ‘O’ కేంద్రంగా గల వృత్తంలో PQ = 12 సెం.మీ., PR = 5 సెం.మీ., వ్యాసం QR అయిన షేడ్ చేయబడిన ప్రాంత వైశాల్యాన్ని కనుగొనండి. (ఇక్కడ TT = 22 గా తీసుకొనుము)

సాధన.
ఇక్కడ ‘PQ’ = 12 సెం.మీ.
‘PR’ = 5 సెం.మీ.
‘QR’ వ్యాసము
PQOR ఒక అర్ధవృత్తము అర్ధవృత్తములో కోణము = 90°.
∴ ∆QPR = 90°
∴ ∆POR ఒక లంబకోణ త్రిభుజము .
∴ ∆PQR వైశాల్యము = [latex]\frac{1}{2}[/latex] bh
= [latex]\frac{1}{2}[/latex] × PQ × PR
= [latex]\frac{1}{2}[/latex] × 12 × 5 = 30 సెం.మీ² …………..(1)
షేడ్ చేయబడిన వృత్తఖండ వైశాల్యం = అర్ధవృత్త వైశాల్యం – ∆PQR వైశాల్యం
= [latex]\frac{1}{2}[/latex] πr² – 30 సెం.మీ.² . ………(2)
∆PQR లో QR² = PQ² + PR²2 (పైథాగరస్ సిద్ధాంతం నుండి)
QR²2 = 12² + 5²
= 144 + 25 = 169 = 13²
∴ QR = 13
వృత్త వ్యాసార్ధము (r) = QO = [latex]\frac{\mathrm{QR}}{2}[/latex]
= [latex]\frac{13}{2}[/latex] = 6.5 సెం.మీ.
అర్ధవృత్త వైశాల్యము = [latex]\frac{1}{2}[/latex] πr²
= [latex]\frac{1}{2}[/latex] × [latex]\frac{22}{7}[/latex] × [latex]\frac{13}{2}[/latex] × [latex]\frac{13}{2}[/latex]
= 66.39 సెం.మీ.² ………..(3)
(1) మరియు (3) లను (2) లో ప్రతిక్షేపించగా
∴ షేడ్ చేయబడిన వృత్తఖండ వైశాల్యం
= (66.39 – 30)
= 36.39 సెం.మీ.²

These AP 10th Class Maths Chapter Wise Important Questions 8th Lesson సరూప త్రిభుజాలు will help students prepare well for the exams.

AP Board 10th Class Maths 8th Lesson Important Questions and Answers సరూప త్రిభుజాలు

ప్రశ్న 1.
ఒక చతురస్రం దీర్ఘ చతురస్రానికి సరూపాలా ? సమర్థించండి.
సాధన.
ఒక చదరము మరియు ఒక దీర్ఘచతురస్రమునందు అనురూపకోణాలు సమానముగా ఉండును. కాని అనురూప భుజాలు అనుపాతములో ఉండవు.

∴ ఒక చదరము మరియు ఒక దీర్ఘచతురస్రములు సరూపములు కావు.

ప్రశ్న 2.
∆ABC లో LM//BC మరియు [latex]\frac{A L}{L B}=\frac{2}{3}[/latex] AM = 5 సెం.మీ. అయిన AC ఎంత?
సాధన.

[latex]\frac{\mathrm{AL}}{\mathrm{LB}}=\frac{\mathrm{AM}}{\mathrm{MC}}[/latex]
[latex]\frac{2}{3}=\frac{5}{M C}[/latex]
MC = [latex]\frac{15}{2}[/latex] = 7.5 సెం.మీ.
AC = AM + MC = 5 + 7.5 = 12.5 సెం.మీ.

ప్రశ్న 3.
∆ABC త్రిభుజములో DE || BC మరియు AC = 5.6 సెం.మీ., AE = 2.1 సెం.మీ. అయిన AD : DB ను కనుగొనుము. June 2018
సాధన.

∆ABC లో DE || BC,
AE = 2.1 సెం.మీ.
EC = AC – AE
= 5.6 – 2.1 BL
= 3.5 సెం.మీ.
ప్రాథమిక అనుపాత సిద్ధాంతం ప్రకారం AD : DB = AE : EC
= 2.1 : 3.5 = 3 : 5

ప్రశ్న 4.
ఇవ్వబడిన పటంలో [latex]\overline{\mathbf{A B}}[/latex] || [latex]\overline{\mathbf{Q R}}[/latex] మరియు PA= 2 సెం.మీ., AQ = 3 సెం.మీ. అయిన ∆POR మరియు ∆PAB ల యొక్క వైశాల్యాల నిష్పత్తి కనుగొనండి.
సాధన.

దత్తాంశము AB || QR; PA = 2, AQ = 3
∆POR ~ ∆PAB
∴ PQ = 2 + 3 = 5
∴ సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి, వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము.

ప్రశ్న 5.

పై పటంలో ∠BAC = ∠CED అయితే ‘x’ యొక్క విలువ 3 అగునో, కాదో సరిచూడుము.
సాధన.
దత్తాంశం ప్రకారం, ∆ABC మరియు ∆ECD లో
∠A = ∠E
∠ACB = ∠ECD [∵ శీర్షాభిముఖ కోణాలు)
∴ ∠B = ∠D[∵ ఉమ్మడి కోణం ]
∴ ∆ABC ~ ∆EDC
⇒ [latex]\frac{A B}{E D}=\frac{B C}{D C}=\frac{A C}{E C}[/latex]
⇒ [latex]\frac{36}{12}=\frac{9}{x}[/latex]
⇒ 36x = 108
⇒ x = [latex]\frac{108}{36}[/latex] = 3.

ప్రశ్న 6.
7.2 సెం.మీ. పొడవు గల ఒక రేఖాఖండమును గీచి దానిని 5 : 3 నిష్పత్తిలో (వృత్తలేఖని, స్కేలును ఉపయోగించి) విభజించండి.
సాధన.

ప్రశ్న 7.
4.2 సెం.మీ., 5.1 సెం.మీ. మరియు 6 సెం.మీ. కొలతలతో త్రిభుజాన్ని నిర్మించండి. దీనితో సరూపంగా ఉంటూ ఈ త్రిభుజ భుజాలకు 2/3 రెట్లు అనురూప భుజాలు గల కొలతలతో త్రిభుజాన్ని నిర్మించండి.
సాధన.

నిర్మాణం :
1. AB = 4.2 cm, BC = 5.1 cm, CA = 6 cm కొలతలతో ∆ABC నిర్మించితిని.
2. BCకు శీర్షం A ఉన్నవైపుకు వ్యతిరేక దిశలో అల్పకోణం చేయునట్లు BX కిరణమును గీచితిని.
3. BB₁ = B₁B₂ = B₂B₃ అగునట్లు BX కిరణముపై B₁, B₂, B₃ అనే మూడు బిందువులు గుర్తించితిని.
4. B₃, C లను కలిపితిని. B₃C కి సమాంతరంగా ఉండునట్లు B₂C¹ ను BC పై గీచితిని.
5. C¹ నుండి CA కి సమాంతరంగా AB మీదకు ఒక రేఖ గీచితిని. అది AB ని A¹ వద్ద ఖండించినది.
6. ∆A¹BC¹ కావలసిన త్రిభుజము.

ప్రశ్న 8.
QR = 5.5 సెం.మీ., ∠Q = 65°, PQ = 6 సెం.మీ. కొలతలు గల త్రిభుజం PQR ని నిర్మించి, దీనితో సరూపంగా వుంటూ, త్రిభుజ భుజాలకు 2/3 రెట్లు అనురూప భుజాల కొలతలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.

నిర్మాణక్రమము :
1) QR = 5.5 సెం.మీ., ∠Q = 65°, PQ = 6 సెం.మీ., కొలతలు గల ∆PQR నిర్మించితిని…
2) Q వద్ద ∠RQX అల్పకోణ కిరణం గీచితిని.
3) [latex]\overline{\mathrm{QX}}[/latex] పై QS₁ = S₁S₂ = S₂S₃ అగునట్లు S₁, S₂, S₃ గుర్తించితిని.
4) S₃ R కలిపితిని.
5) S₃ R కు సమాంతరంగా S₂ R’ మరియు PR కు సమాంతరంగా P’R’ గీచితిని. .
∴ ∆POR ~ ∆P’QR’.

ప్రశ్న 9.
(i) ప్రాథమిక అనుపాత సిద్ధాంతాన్ని ప్రవచించి, నిరూపించండి.
(ii) పై సిద్దాంతాన్ని ఉపయోగించి క్రింది పటంలో ఇవ్వబడిన AE పొడవును కనుగొనండి. AD = 1.8 సెం.మీ., BD = 5.4 సెం.మీ., EC = 7.2 సెం.మీ.
సాధన.

ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి.
దత్తాంశము : ∆ABC లో DE || BC, DE రేఖ AB, AC భుజాలను వరుసగా D మరియు E వద్ద ఖండించును.
సారాంశము : [latex][/latex]
నిర్మాణము : B; E మరియు C, D లను కలుపుము మరియు DM ⊥ AC, EN ⊥ AB లను గీయుము.
ఉపపత్తి : ∆ADE వైశాల్యము = [latex]\frac{1}{2}[/latex] × AD × EN
∆BDE వైశాల్యము = [latex]\frac{1}{2}[/latex] × BD × EN

కావున

మరల ∆ADE వైశాల్యము = [latex]\frac{1}{2}[/latex] × AE × DM
∆CDE వైశాల్యము = [latex]\frac{1}{2}[/latex] × EC × DM
= [latex]\frac{\frac{1}{2} \times \mathrm{AE} \times \mathrm{DM}}{\frac{1}{2} \times \mathrm{EC} \times \mathrm{DM}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex] …………….. (2)
∆BDE, ∆CDE లు ఒకే భూమి DE మరియు సమాంతర రేఖలు BC మరియు DE ల మధ్య ఉన్నట్లు గమనించవచ్చును.
కావున ∆BDE వైశాల్యము = ∆CDE వైశాల్యము …………….. (3)
(1), (2), (3) ల నుండి [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex] కావున సిద్ధాంతము నిరూపించబడినది.

(ii)
AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
పై సిద్ధాంతమునుండి [latex]\frac{A D}{B D}=\frac{A E}{E C}[/latex]
⇒ AE = [latex]\frac{(\mathrm{AD})(\mathrm{EC})}{\mathrm{BD}}=\frac{1.8 \times 7.2}{5.4}[/latex] = 2.4
∴ AE = 2.4 సెం.మీ.

ప్రశ్న 10.
4.3 సెం.మీ., 5.2 సెం.మీ. మరియు 6.5 సెం.మీ. భుజాలుగా కల్గిన త్రిభుజాన్ని నిర్మించి, దానికి సరూపంగా ఉంటూ అనురూప భుజాలలో 3/5 భాగం కల్గిన వేరొక త్రిభుజాన్ని నిర్మించండి. …
సాధన.

నిర్మాణం :
1. AB = 4.3 సెం.మీ., BC = 5.2 సెం.మీ. , CA = 6.5 సెం.మీ. కొలతలతో AABC నిర్మించితిని.
2. BC కు శీర్షం A ఉన్నవైపుకు వ్యతిరేక దిశలో అల్పకోణం చేయునట్లు BX కిరణమును గీచితిని.
3. BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ అగునట్లు BX కిరణముపై B₁, B₂, B₃, B₄, B₅. అనే ఐదు బిందువులు గుర్తించితిని.
4. B₅, C లను కలిపితిని: B₃C కి సమాంతరంగా ఉండునట్లు B, C’ను BC పై గీచితిని.
5. C’ నుండి CA కి సమాంతరంగా AB మీదకు ఒక రేఖ గీచితిని అది ABని A’ వద్ద ఖండించినది.
6. ∆A’BC’ కావలసిన త్రిభుజము.

ప్రశ్న 11.
AB = 4 సెం.మీ., BC = 6 సెం.మీ. మరియు AC = 4 సెం.మీ. కొలతలు గల త్రిభుజం ABC, నిర్మించుము. ఈ త్రిభుజానికి సరూపంగా ఉంటూ, ఈ త్రిభుజ భుజాలకు 3/4 రెట్లు అనురూప భుజాల కొలతలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.

These AP 10th Class Maths Chapter Wise Important Questions 7th Lesson రేఖాగణితం will help students prepare well for the exams.

AP Board 10th Class Maths 7th Lesson Important Questions and Answers రేఖాగణితం

ప్రశ్న 1.
(2, 0) మరియు (0, 2) బిందువులను కలుపు రేఖా
ఖండాన్ని 1 : 1 నిష్పత్తిలో విభజించే బిందువు నిరూపకా . లను కనుగొనండి.
సాధన.
x₁ = 2 ; x₂ = 0; y₁ = 0; y₂ = 2
1 : 1 నిష్పత్తిలో విభజించు బిందు నిరూపకాలు (లేదా) మధ్య బిందువు నిరూపకాలు
= [latex]\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)[/latex]
= [latex]\left(\frac{2+0}{2}, \frac{0+2}{2}\right)[/latex]
= (1, 1).

ప్రశ్న 2.
(a cos θ, 0) మరియు (0, a sin θ) బిందువుల మధ్య దూరము కనుగొనుము.
సాధన.
(a cos θ, 0) మరియు (0, a sin θ) బిందువుల మధ్య దూరం (x₁, y₁) మరియు (x₂, y₂) బిందువుల మధ్య దూరమునకు సూత్రము :
= (x, – X2)2 + (y! – y )2 నందు
x₁ = a cos θ, y₁ = 0;
x₂ = 0, y₂ = a sin θ ప్రతిక్షేపించగా
పై బిందువుల మధ్య దూరం = [latex]\sqrt{(a \cos \theta-0)^{2}+(0-a \sin \theta)^{2}}[/latex]
= [latex]\sqrt{\mathrm{a}^{2} \cos ^{2} \theta+\dot{\mathrm{a}}^{2} \sin ^{2} \theta}[/latex]
= [latex]\sqrt{a^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)}[/latex]
= [latex]\sqrt{a^{2}(1)}=\sqrt{a^{2}}[/latex] = a
∴ వాని మధ్య దూరం = a యూనిట్లు.

ప్రశ్న 3.
A(4, 0), B(0, y) మరియు AB = 5 అయిన లకు సాధ్య విలువలు కనుక్కోండి.
సాధన.
A(4, 0); B(0 y); AB = 5 .
[latex]\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}[/latex] = 5
[latex]\sqrt{16+y^{2}}[/latex] = 5
√16 + y² = 5
16 + y² = 25
y² = 25 – 16 = 9
y = ± √9 = ± 3
yకు సాధ్యపడు విలువలు 3 లేదా – 3.

ప్రశ్న 4.
(3, 2) కేంద్రంగా ఉంటూ (4, – 1) బిందువు గుండా పోయే వృత్త వ్యాసార్థాన్ని కనుగొనుము.
సాధన.

వ్యాసార్ధం = AB
బిందువుల మధ్య దూరం = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]

వ్యాసార్థం ‘r’ = [latex]\sqrt{(4-3)^{2}+(-1-2)^{2}}[/latex]

= [latex]\sqrt{(1)^{2}+(-3)^{2}}[/latex]

= [latex]\sqrt{1+9}=\sqrt{10}[/latex] యూ.

ప్రశ్న 5.
∆ABC త్రిభుజము యొక్క మూడు శీర్షాలు A(3, – 2), B(- 5, 4) మరియు C(2, – 2) అయిన దాని గురుత్వ కేంద్రము గురించి ఏమి పరిశీలించితివి?
సాధన.
త్రిభుజ గురుత్వ కేంద్రము
= [latex]\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)[/latex]

= [latex]\left(\frac{3+(-5)+2}{3}, \frac{-2+4+(-2)}{3}\right)[/latex] = (0,0)
గురుత్వ కేంద్రము మూలబిందువు అని పరిశీలించితిని.

ప్రశ్న 6.
(6, 2), (0, 0) మరియు (4, – 5) శీర్ష బిందువులుగా కల్గిన త్రిభుజ గురుత్వ కేంద్రాన్ని కనుగొనండి.
సాధన.

త్రిభుజ శీర్షబిందువులు = (6, 2) (0, 0) మరియు (4, – 5)
గురుత్వ కేంద్రము = [latex]\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)[/latex]

= [latex]\left(\frac{6+0+4}{3}, \frac{2+0-5}{3}\right)[/latex]

= [latex]\left(\frac{10}{3}, \frac{-3}{3}\right)=\left(\frac{10}{3},-1\right)[/latex]

ప్రశ్న 7.
(3, 2) బిందువు కేంద్రంగా (-5, 6) బిందువు గుండా పోయే వృత్తవ్యాసార్ధమును కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, వృత్తం A (3, 2) బిందువు కేంద్రంగా B (- 5, 6) బిందువు గుండా పోతుంది.

వ్యాసార్ధం = AB [∵ వృత్త కేంద్రం నుండి బిందువుకు గల దూరం]
దూరం = [latex]\sqrt{\left(\mathrm{x}_{2} \cdot-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}[/latex]
వ్యాసార్ధం ‘r’ = [latex]\sqrt{(-5-3)^{2}+(6-2)^{2}}[/latex]
= √64 + 16 = √80
= √16 x 5 = 4√5 యూ.

ప్రశ్న 8.
(0, – sin x) మరియు (- cos x, 0) ల మధ్య దూరం కనుగొనండి.
సాధన.
(0, – sin x) మరియు (- cos x, 0) ల మధ్య దూరం
= [latex]\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}[/latex]
= [latex]\sqrt{(-\cos x-0)^{2}+(0+\sin x)^{2}}[/latex]
= [latex]\sqrt{\cos ^{2} x+\sin ^{2} x}[/latex] = √1 = 1 యూ.

ప్రశ్న 9.
బిందువులు (0, – 3) మరియు (-8, 0) లు నిరూపక తలంలో ఎక్కడ ఉంటాయో తెల్పండి.
సాధన.
(0, – 3) బిందువు నందు X నిరూపకం = 0 కావున ఈ బిందువు Y – అక్షంపై ఉండును. మరియు ఈ బిందువు యొక్క Y నిరూపకం – 3 అనగా ఋణాత్మకం కావున OY పై ఉంటుంది. అదే విధంగా బిందువు (- 8, 0) నందు Y నిరూపకం విలువ ‘O’ కావున ఇది X – అక్షంపై ఉండును. మరియు దీనియొక్క X నిరూపకం – 8 అనగా ఋణాత్మకం కావున OX పై ఉంటుంది.

ప్రశ్న 10.
(7, 2), (5, 1) మరియు (3, k) బిందువులు సరేఖీయాలైతే k విలువెంత ?
సాధన.
బిందువులు సరేఖీయాలైన ఆ బిందువులతో ఏర్పడు
త్రిభుజ వైశాల్యం = 0
త్రిభుజ వైశాల్యం = [latex]\frac{1}{2}[/latex] [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= [latex]\frac{1}{2}[/latex] |7(1 – k) + 5(k – 2) + 3(2 – 1)|
= [latex]\frac{1}{2}[/latex] | – 2k| = 0
∴ k = 0

ప్రశ్న 11.
(- 4, 4), (- 2, 2) మరియు (6, – 6) బిందువులను శీర్షములుగా కలిగిన త్రిభుజ గురుత్వ కేంద్రమును కనుక్కోండి.
సాధన.
త్రిభుజ గురుత్వ కేంద్రము
= [latex]\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)[/latex]
= [latex][/latex]= (0, 0).

ప్రశ్న 12.
బిందువులు (x, 1) మరియు (- 1, 5) ల మధ్య దూరము ‘5’ యూనిట్లు అయిన ‘x’ విలువ ఎంత ?
సాధన.
రెండు బిందువుల మధ్య దూరం = [latex]\sqrt{\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)^{2}}[/latex]
(x, 1), (- 1, 5) బిందువుల మధ్య దూరం = 5
[latex]\sqrt{[x-(-1)]^{2}+(1-5)^{2}}[/latex] = 5
[latex]\sqrt{(x+1)^{2}+(-4)^{2}}[/latex] = 5
x² + 1 + 2x + 16 = 25
x² + 2x – 8 = 0
(x + 4) (x – 2) = 0
x = – 4 లేదా x = 2.

ప్రశ్న 13.
5 సెం.మీ., 12 సెం.మీ., 13 సెం.మీ. భుజములుగా గల త్రిభుజ వైశాల్యమును హెరాన్ సూత్రము ద్వారా, కనుగొనుము.
సాధన.
a = 5 సెం.మీ., b = 12 సెం.మీ., c = 13 సెం.మీ. అనుకొనుము
s = [latex]\frac{a+b+c}{2}=\frac{5+12+13}{2}[/latex] = 15
త్రిభుజ వైశాల్యం (∆) (∆) = [latex]\sqrt{s(s-a)(s-b)(s-c)}[/latex]
= [latex]\sqrt{15(15-5)(15-12)(15-13)}[/latex]
= 30 సెం.మీ.²

ప్రశ్న 14.
గ్రాఫ్ ను పరిశీలించి, క్రింది ప్రశ్నలకు జవాబులివ్వండి.

(i) A మరియు B బిందువుల నిరూపకాలు రాయండి.
(ii) [latex]\overrightarrow{\mathbf{A B}}[/latex] సరళరేఖ యొక్క వాలు కనుగొనండి.
సాధన.
(i) ‘A’ బిందు నిరూపకము = (0, 2)
‘B’ బిందు నిరూపకము = (- 3, 0)

(ii) వాలు = [latex]\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{0-2}{-3-0}=\frac{-2}{-3}=\frac{2}{3}[/latex]

ప్రశ్న 15.
(1, 5), (2, 5) మరియు (-2, – 1) బిందువులు సరేఖీయాలు అగునో, కావో కనుగొనండి.
సాధన.
A(1, 5), B(2, 5), C(- 2, – 1)
మధ్య దూరం = [latex]\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}[/latex]
AB = [latex]\sqrt{(2-1)^{2}+(5-5)^{2}}[/latex]
= [latex]\sqrt{1+0}[/latex] = 1

BC = [latex]\sqrt{(-2-2)^{2}+(-1-5)^{2}}[/latex]
= [latex]\sqrt{16+36}=\sqrt{52}=2 \sqrt{13}[/latex]

CA = [latex]\sqrt{(1+2)^{2}+(5+1)^{2}}[/latex]
= [latex]\sqrt{9+36}=\sqrt{45}=3 \sqrt{5}[/latex]

ప్రశ్న 16.
AB ఒక వృత్త వ్యాసము. కేంద్రము (2, -3) మరియు B (1, 4) అయితే, A నిరూపకాలు కనుక్కోండి.
సాధన.

మదబిందువు = [latex]\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}[/latex]
[latex]\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}[/latex] = a… (1)
[latex]\frac{x+1}{2}[/latex] = 2
x + 1 = 4
x = 4 – 1 = 3
x = 3

[latex]\frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}[/latex] = b …………. (2)
[latex]\frac{y+4}{2}[/latex] = – 3
y + 4 = – 6
y = – 10
∴ A = 3, – 10.

ప్రశ్న 17.
ఈ క్రింద ఇవ్వబడిన బిందువులు సరేఖీయాలు అవుతాయా ? కాదా ? సరిచూడండి. (1, – 1), (4, 1), (- 2, -3 )
సాధన.
త్రిభుజం యొక్క వైశాల్యం ‘సున్న అయితే ఇవ్వబడిన మూడు బిందువులు సరేఖీయాలు అవుతాయి. ఇవ్వబడిన బిందువులు (1, – 1), (4, 1), (- 2, – 3)
త్రిభుజం యొక్క వైశాల్యం ∆ = [latex]\frac{1}{2}[/latex] |x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
= [latex]\frac{1}{2}[/latex] |1(1 + 3) + 4(- 3 + 1) – 2 (-1 – 1)|
= [latex]\frac{1}{2}[/latex] |4 – 8 + 4|
= [latex]\frac{1}{2}[/latex] |8 – 8|
= [latex]\frac{1}{2}[/latex] |0| = 0
కావున, మూడు బిందువులు సరేఖీయాలు.

ప్రశ్న 18.
(3, 0), (6, 4) మరియు (-1, 3) బిందువులు లంబకోణ సమద్విబాహు త్రిభుజ శీర్షాలు అవుతాయో లేదో సరి చూడండి. త్రిభుజ వైశాల్యం కూడా కనుగొనుము.
సాధన.
A(3, 0), B(6, 4) బిందువుల మధ్య దూరం

AB = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]
= [latex]\sqrt{(6-3)^{2}+(4-0)^{2}}[/latex]
= [latex]\sqrt{9+16}[/latex] = 5 యూ.

B(6, 4), C(- 1, 3) బిందువుల మధ్య దూరం
BC = [latex]\sqrt{(-1-6)^{2}+(3-4)^{2}}[/latex]
= [latex]\sqrt{(-7)^{2}+(-1)^{2}}=\sqrt{50}[/latex] యూ.

C(- 1, 3), A(3, 0) బిందువుల మధ్య దూరం
CA = [latex]\sqrt{[3-(-1)]^{2}+(0-3)^{2}}[/latex]
= [latex]\sqrt{16+9}[/latex] = 5 యూ.
∴ AB² = 25, BC² = 50, CA² = 25,
BC² = AB² + CA² మరియు AB = CA
∴ ∆ ABC లంబకోణ సమద్విబాహు, త్రిభుజం అవుతుంది.
∴ ∆ ABC వైశాల్యం = [latex]\frac{1}{2}[/latex] × AB × AC
= [latex]\frac{1}{2}[/latex] × 5 × 5 = 12.5 చ. యూ.

ప్రశ్న 19.
(2, 3), (- 1, 3) మరియు (2, – 1) బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యమును హెరాన్ సూత్రమును ఉపయోగించి కనుగొనుము.
సాధన.
(2, 3) (- 1, 3) మరియు (2, – 1) బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యంను హెరాన్ సూత్రంను ఉపయోగించి కనుగొనుట.
పటంలో చూపినట్లు ∆ABC యొక్క శీర్షాల నిరూపకాలు A(2, 3) ; B(- 1, 3) మరియు C(2, – 1) అనుకుందాం.

∴ ఆ త్రిభుజ భుజాల పొడవులు AB = c, BC = a, CA = b తో సూచిస్తాం.
హెరాన్ సూత్ర పద్ధతిన త్రిభుజ వైశాల్యము = [latex]\sqrt{s(s-a)(s-b)(s-c)}[/latex]
ఇక్కడ s = [latex]\frac{a+b+c}{2}[/latex] కావున మనం భుజాల పొడవులు కనుగొందాం.

భుజాల పొడవులను [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex] సూత్ర సహాయాన కనుగొందాం.
∴ AB = c = (2, 3) మరియు (- 1, 3) బిందువుల మధ్య దూరం.
c = [latex]\sqrt{(2-(-1))^{2}+(3-3)^{2}}[/latex]
= [latex]\sqrt{(2+1)^{2}+0^{2}}[/latex]
= [latex]\sqrt{3^{2}+0}=\sqrt{3^{2}}[/latex] = 3

మరియు BC = a = (- 1, 3) మరియు (2, – 1) ల మధ్య దూరం
a = [latex]\sqrt{(-1-2)^{2}+[3-(-1)]^{2}}[/latex]
= [latex]\sqrt{(-3)^{2}+(3+1)^{2}}[/latex]
= [latex]\sqrt{9+16}=\sqrt{25}[/latex] = 5

మరియు CA = b = (2, – 1) మరియు (2, 3) బిందువుల మధ్య దూరం b = [latex]\sqrt{(2-2)^{2}+(-1-3)^{2}}[/latex]
= [latex]\sqrt{0^{2}+4^{2}}=\sqrt{16}[/latex] = 4
∴ a = 5, b = 4, c = 3
⇒ s = [latex]\frac{a+b+c}{2}=\frac{5+4+3}{2}=\frac{12}{2}[/latex] = 6
∴ ∆ABC వైశాల్యము = [latex]\sqrt{s(s-a)(s-b)(s-c)}[/latex]
= [latex]\sqrt{6(6-5)(6-4)(6-3)}[/latex]
= [latex]\sqrt{6(1)(2)(3)}=\sqrt{6 \times 6}[/latex] = 6 చ||యూ.
∴ ఇచ్చిన త్రిభుజ వైశాల్యము = 6 చ||యూ.

 

ప్రశ్న 20.
బిందువులు A(6, 1), B (8, 2), C(9, 4) మరియు D(p, 3) లు వరుసగా సమాంతర చతుర్భుజ శీర్యాలయిన,
(i) p యొక్క విలువను కనుగొనుము.
(ii) ▱ ABCD వైశాల్యమును కనుగొనుము.
సాధన.
(i) A, B, C, D లు సమాంతర చతుర్భుజ శీర్షాలు
కావున AC మధ్య బిందువు = BD మధ్య బిందువు

A(6, 1) = (x₁, y₁); C(9, 4) = (x₂, y₂)
AC మధ్య బిందువు = [latex]\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)[/latex]
= [latex]\left(\frac{6+9}{2}, \frac{1+4}{2}\right)[/latex]
= [latex]\left(\frac{15}{2}, \frac{5}{2}\right)[/latex]

B(8, 2) = (x₁, y₁); D(p, 3) = (x₂, y₂)
BD మధ్య బిందువు = [latex]\left(\frac{8+p}{2}, \frac{2+3}{2}\right)[/latex]
= [latex]\left(\frac{8+p}{2}, \frac{5}{2}\right)[/latex]
∴ [latex]\frac{8+p}{2}=\frac{15}{2}[/latex]
∴ p = 7.

(ii) ∆ABC వైశాల్యము = [latex]\frac{1}{2}[/latex] |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= [latex]\frac{1}{2}[/latex] |6(2 – 4) + 8(4 – 1) + 9(1 – 2)|
= [latex]\frac{1}{2}[/latex] |- 12 + 24 – 9|
= [latex]\frac{1}{2}[/latex] |3| = [latex]\frac{3}{2}[/latex]
∴ సమాంతర చతుర్భుజం ABCD వైశాల్యము = 2 × ∆ABC వైశాల్యము
= 2 × [latex]\frac{3}{2}[/latex] = 3 చ.యూ.

ప్రశ్న 21.
‘k’ యొక్క ఏ విలువకు బిందువులు (3k – 1, k – 2), (k, k – 7) మరియు (k – 1, – k – 2) లు సరేఖీయాలగును?
సాధన.
దత్త బిందువులు సరేఖీయాలు. . అనగా A (3k – 1, k – 2), B (k, k – 7) మరియు C (k – 1, – k – 2) బిందువులు ABC రేఖపై ఉండును.
[latex]\overline{\mathrm{AB}}[/latex] మరియు [latex]\overline{\mathrm{AC}}[/latex] ల వాలులు సమానము. (∵ అవి సరేఖీయాలు)
వాలు = y – నిరూపకాల భేదం / x – నిరూపకాల భేదం
= [latex]\frac{y_{2}-y_{1}}{x_{2}-x_{1}}[/latex]

[latex]\overline{\mathrm{AB}}[/latex] వాలు = [latex]\frac{(\mathrm{k}-7)-(\mathrm{k}-2)}{\mathrm{k}-(3 \mathrm{k}-1)}[/latex]
= [latex]\frac{k-7-k+2}{k-3 k+1}[/latex]
= [latex]\frac{-5}{1-2 k}[/latex] ………………(1)

A(3k – 1, k – 2), C(k – 1, – k – 2)
[latex]\overline{\mathrm{AC}}[/latex] వాలు = [latex]\frac{(-k-2)-(k-2)}{(k-1)-(3 k-1)}[/latex]
= [latex]\frac{-k-2-k+2}{k-1-3 k+1}[/latex]
= [latex]\frac{-2 \mathrm{k}}{-2 \mathrm{k}}[/latex] = 1
(1) = (2)
⇒ [latex]\frac{-5}{1-2 k}[/latex] = 1
⇒ 1 – 2k = – 5
⇒ 1 + 5 = 2k
⇒ 2k = 6
∴ k = 3

These AP 8th Class Biology Important Questions 9th Lesson జంతువుల నుండి ఆహారోత్పత్తి will help students prepare well for the exams.

AP Board 8th Class Biology 9th Lesson Important Questions and Answers జంతువుల నుండి ఆహారోత్పత్తి

ప్రశ్న 1.
పశుపోషణ ఆవశ్యకత ఏమిటి ?
జవాబు:

1. పశుపోషణ వలన మనకు పాలు వాటి ఆహార ఉత్పత్తులు లభిస్తాయి.
2. వ్యవసాయంలో పశువుల పాత్ర కీలకం.
3. రవాణాలో కూడ పశువులను వాడుతున్నాము.
4. పశు వ్యర్థాలను కంపోస్ట్ ఎరువుగా వాడుతున్నారు.
5. పశువుల పేడ నుండి బయోగ్యాస్ తయారుచేస్తారు.
6. భారతదేశం వంటి దేశాలలో పశుపోషణ వ్యవసాయంలో అంతర్భాగంగా ఉంది.

ప్రశ్న 2.
వరి పొలాలలో చేపలు పెంచటం వలన కలిగే ప్రయోజనం ఏమిటి ?
జవాబు:

1. ఈ మధ్య కాలంలో రైతులు వరి పంటతో పాటుగా పొలంలో చేపలు కూడా పెంచుతున్నారు.
2. వరిచేనులోని నీటిలోనే చేపలను పెంచుతారు.
3. వరిపొలంలో చేపలను పెంచడం అనేది అనేక రకాలుగా ఉపయోగమైన పద్ధతి.
4. వరి పొలాలలో రసాయనిక ఎరువులు, కీటక సంహారిణులు ఎక్కువ వాడటం వలన వెలువడే విష రసాయనాలు చేపలు, పక్షులు, పాములపై తీవ్ర ప్రభావం చూపుతున్నాయి.
5. వరిపొలంలో చేపలను పెంచడం వలన వరిలో కాండం తొలుచు పురుగు వంటి వ్యాధులను అరికట్టవచ్చు.
6. అందువల్ల రసాయనాల వినియోగం తగ్గుతుంది. పర్యావరణం కాపాడబడుతుంది.

ప్రశ్న 3.
గుడ్డులోని పోషకవిలువలు గురించి రాయండి.
జవాబు:
గుడ్డు మంచి పౌష్టిక ఆహారము. అది అనేక పోషకాలను కల్గి ఉంది. దీనిలో
కార్బోహైడ్రేట్స్ – 1.12 గ్రా.
కేలరీస్ – 647 కి.జె.
ప్రొటీన్స్ – 12.6 గ్రా.
క్రొవ్వు – 10.6 గ్రా.
విటమిన్ A – 19%
థయామిన్ – 0.066 మి.గ్రా. (6%)
రైబోఫ్లెవిన్ – 0.5 మి.గ్రా. (42%)
విటమిన్ D – 87 IU
విటమిన్ E – 1.03 మి.గ్రా.
కాల్షియం – 50 మి.గ్రా.
ఐరన్ – 1.2 మి.గ్రా.
మెగ్నీషియం – 10 మి.గ్రా.
ఫాస్పరస్ – 172 మి.గ్రా.
కొలెస్టరాల్ – 126 మి.గ్రా. ఉన్నాయి

ప్రశ్న 4.
పాల శీతలీకరణ కేంద్రాలలో పాలలోని సూక్ష్మజీవులను నాశనం చేసి, పాలను నిల్వచేసే పద్ధతిని వివరించండి.
జవాబు:

1. పాల శీతలీకరణ కేంద్రాలలో పాలను 72 ( వద్ద 30 నిమిషాల పాటు వేడిచేసి హఠాత్తుగా 10 కన్నా తక్కువ ఉష్ణోగ్రతల వద్ద శీతలీకరిస్తారు. ఈ ప్రక్రియను పాశ్చరైజేషన్ అంటారు.
2. దీనివలన పాలు సూక్ష్మజీవరహితం చేయబడి ఎక్కువ కాలం నిల్వ ఉంటాయి.
3. ఈ పద్ధతిని లూయిస్ పాశ్చర్ కనిపెట్టాడు.

ప్రశ్న 5.
పశువుల పెంపకంలో అనుబంధ ఉత్పత్తులు, పరిశ్రమల గురించి రాయండి. (లేదా) ఆవుపేడ జీవ ఇంధనంగా ఉపయోగపడుతుంది. ఇది ఒక అనుబంధ పదార్దమేకదా! పశుసంవర్థనంలో ఉత్పత్తి అయ్యే ఇలాంటి కొన్ని అనుబంధ ఉత్పత్తుల గురించి రాయండి.
జవాబు:
పశువుల పెంపకంలో అనుబంధ ఉత్పత్తులు :
మాంసం, పేడ, తోళ్ళు, ఎముకలు, చర్మం, వాటి కొమ్ములు.
పరిశ్రమలు :

1. డైరీ పరిశ్రమ : దీనిలో పాలు, పాల ఉత్పత్తులు చేస్తారు.
2. కబేల (పశువధశాల) : ఎద్దు మాంసం ఇక్కడ తయారుచేస్తారు.
3. తోళ్ళ పరిశ్రమ : ఇక్కడ తోళ్లను శుభ్రపరిచి పర్సులు, బెలు, చెప్పులు తయారుచేస్తారు.
4. ఎరువుల పరిశ్రమ : పేడను ఉపయోగించి బయోగ్యాస్ తయారుచేస్తారు.
5. బయోగ్యాస్ పరిశ్రమ : పశువుల ఎముకలను ఎరువుల కర్మాగారాలలో వాడతారు.
6. వస్తువులు తయారుచేసే పరిశ్రమ : పశువుల చర్మం, కొమ్ములను ఉపయోగించి వివిధ రకాల ఆట మరియు అలంకార వస్తువులు తయారుచేస్తారు.

1 మార్కు ప్రశ్నలు

ప్రశ్న 1.
నదీముఖ ద్వారాలు అనగానేమి ? అవి సముద్రపు మరియు నీటి చేపలు నివసించటానికి ఎలా అనువుగా ఉంటాయి ?
జవాబు:
నదీముఖ ద్వారాలు అనగా నదులు సముద్రంలో కలిసే చోటు. నదీముఖ ద్వారాలలో సముద్రపు మరియు మంచినీటి చేపలు నివసించటానికి ఎలా అనువుగా ఉంటుంది అంటే ఈ ప్రాంతాలలో నివసించే చేపలు లవణీయత వ్యత్యాసాన్ని తట్టుకొనే శక్తిని కలిగి ఉంటాయి.

ప్రశ్న 2.
శ్వేత విప్లవం అనగానేమి?
జవాబు:
శ్వేత విప్లవం : పాల ఉత్పత్తిని పెంచటం. పాల నుండి లభించే ఇతర పదార్థాల నాణ్యతని, పరిమాణాన్ని పెంచి, సాధ్యమైనంత తక్కువ ధరలో అందరికీ అందించటానికి జరిగిన ప్రయత్నాన్ని శ్వేత విప్లవం అంటారు.

ప్రశ్న 3.
నీలి విప్లవం అనగానేమి?
జవాబు:
నీలి విప్లవం : చేపల పెంపకం. దిగుబడి పెంచటానికి, నాణ్యత అధికం చేయుటకు జరిగిన ప్రయత్నాన్ని నీలి విప్లవం అంటారు.

ప్రశ్న 4.
ఎపిస్ టింక్చర్ అంటే ఏమిటి?
జవాబు:
ఎపిస్ టింక్చర్ : తేనెటీగల విషంతో తయారుచేయబడిన హోమియో మందుని ఎపిస్ టింక్చర్ అంటారు.

ప్రశ్న 5.
చేపలను నిలవ చేయడంలో పాటించే పద్ధతులను వివరించండి.
జవాబు:
చేపలను నిలవ చేయడంలో పాటించే పద్ధతులు
1. ఎండలో ఎండబెట్టడం
2. పాక్షికంగా ఎండబెట్టడం
3. పొగ బెట్టడం
4. ఉప్పులో ఊరబెట్టడం

ప్రశ్న 6.
ఆవు, గేదె, మేక, గొర్రెల పెంపకంలో ఏమైనా తేడాలున్నాయా ?
జవాబు:
ఆవులు, గేదెలు, ఎండిన గడ్డితో పాటు పచ్చిగడ్డి తింటాయి. మేకలు చెట్ల ఆకులను, పచ్చిగడ్డిని ఆహారంగా తీసుకొంటాయి. గొర్రెలు పచ్చిగడ్డిని, నూకలను ఆహారంగా తీసుకుంటాయి.

ప్రశ్న 7.
పశువులను పెంచేవారు సాధారణంగా ఎదుర్కొనే సమస్యలేవి ?
జవాబు:
అనావృష్టి పరిస్థితులలో పశుగ్రాసం కొరత పశువులు పెంచేవారు సాధారణంగా ఎదుర్కొనే సమస్య.

ప్రశ్న 8.
అధిక మొత్తంలో చేపలను పట్టడానికి ఏం చేస్తారు ?
జవాబు:
అధిక మొత్తంలో చేపలు పట్టుకొనుటకు నైలాన్ వలలు ఉపయోగిస్తారు. పెద్ద వలలను, మోటార్ పడవలను ఉపయోగిస్తారు.

లక్ష్యాత్మక నియోజనము

ప్రశ్న 1.
గేదె జాతులలో ప్రసిద్ధ జాతి పేరు :
ఎ) జెర్సీ
బి) హాల్ స్టీన్
సి) ముర్రా
డి) అనోకా
జవాబు:
సి) ముర్రా

ప్రశ్న 2.
ఏనెలలో పాల దిగుబడి చాలా తక్కువగా ఉండును ?
ఎ) జనవరి
బి) ఏప్రిల్
సి) డిసెంబర్
డి) నవంబర్
జవాబు:
బి) ఏప్రిల్

ప్రశ్న 3.
ఆస్ట్రిచ్ గుడ్డు తర్వాత అతిపెద్ద గుడ్డు పెట్టు పక్షి
ఎ) ఈము
బి) ఏనుగు
సి) పావురం
డి) పెంగ్విన్
జవాబు:
ఎ) ఈము

ప్రశ్న 4.
ఏ గేదె పాలు రిఫ్రిజిరేటర్లలో ఉంచకున్నా దాదాపు వారం రోజులపాటు చెడిపోకుండా ఉంటాయి ?
ఎ) ముర్రా
బి) జెర్సీ
సి) కోలేరు
డి) చిల్కా
జవాబు:
డి) చిల్కా

ప్రశ్న 5.
పంది మాంసాన్ని ఏమంటారు ?
ఎ) బీఫ్
బి) పోర్క్
సి) మటన్
డి) చికెన్
జవాబు:
బి) పోర్క్

ప్రశ్న 6.
మాంసం కోసం పెంచే కోళ్ళు
ఎ) లేయర్స్
బి) హెచరీస్
సి) బ్రాయిలర్స్
డి) అనోకా
జవాబు:
సి) బ్రాయిలర్స్

ప్రశ్న 7.
కోడిగ్రుద్దును ఇంక్యుబేటర్స్ ఉపయోగించి పొదిగితే కోడిపిల్ల వచ్చుటకు ఎన్ని రోజులు పట్టును?
ఎ) 21
బి) 15
సి) 18
డి) 10
జవాబు:
ఎ) 21

ప్రశ్న 8.
కోడిపందాల కొరకు పెంచే భారతీయ దేశీయకోడి
ఎ) అనోకా
బి) ఆసిల్
సి) క్లైమౌత్
డి) వైట్ లెగ్ హార్న్
జవాబు:
బి) ఆసిల్

ప్రశ్న 9.
తేనెటీగలలో సోమరులు
ఎ) ఆడ ఈగలు
బి) వంధ్య ఆడ ఈగలు
సి) మగ వంధ్య ఈగలు
డి) మగ ఈగలు
జవాబు:
డి) మగ ఈగలు

ప్రశ్న 10.
కృత్రిమ తేనెపట్టులో ఎన్ని భాగాలుంటాయి ?
ఎ) 2
బి) 6
సి) 4
డి) 1
జవాబు:
బి) 6

ప్రశ్న 11.
ఈ క్రింది వానిలో అత్యంత ప్రాచీన కాలంలోనే మచ్చిక చేసుకున్న జంతువు
ఎ) కుక్క
బి) గొట్టె
సి) పంది
డి) మేక
జవాబు:
ఎ) కుక్క

ప్రశ్న 12.
నట్టల వ్యాధి వీనికి వస్తుంది.
ఎ) కోళ్ళు
బి) ఆవులు, గేదెలు
సి) మేకలు, గొట్టెలు
డి) కుక్కలు
జవాబు:
సి) మేకలు, గొట్టెలు

ప్రశ్న 13.
ప్రపంచంలో పాల ఉత్పత్తి అధికంగా చేస్తున్న దేశం
ఎ) ఇజ్రాయిల్
బి) అమెరికా
సి) జపాన్
డి) భారతదేశం
జవాబు:
ఎ) ఇజ్రాయిల్

ప్రశ్న 14.
దేశీయ గేదె జాతులు రోజుకు సరాసరి ఎన్ని లీటర్ల పాలు యిస్తాయి?
ఎ) 2 నుండి
బి) 2 నుండి 5
సి) 3 నుండి
డి) 3 నుండి 7
జవాబు:
బి) 2 నుండి 5

ప్రశ్న 15.
మనరాష్ట్రంలో పెంచే ముర్రాజాతి గేదెలు రోజుకు ఎన్ని పాలను యిస్తాయి ?
ఎ) 8 లీటర్లు
బి) 10 లీటర్లు
సి) 14 లీటర్లు
డి) 6 లీటర్లు
జవాబు:
ఎ) 8 లీటర్లు

ప్రశ్న 16.
జర్సీ ఆవు ఏ దేశానికి చెందింది ?
ఎ) ఇంగ్లాండ్
బి) డెన్మార్క్
సి) అమెరికా
డి) యూరప్
జవాబు:
ఎ) ఇంగ్లాండ్

ప్రశ్న 17.
సంకరజాతి ఆవు రోజుకు ఎన్ని పాలనిస్తాయి ?
ఎ) 10 లీటర్ల నుంచి 20 లీటర్లు
బి) 8 లీటర్ల నుంచి 20 లీటర్లు
సి) 8 లీటర్ల నుంచి 15 లీటర్లు
డి) 10 లీటర్ల నుంచి 15 లీటర్లు
జవాబు:
బి) 8 లీటర్ల నుంచి 20 లీటర్లు

ప్రశ్న 18.
మనదేశంలో పాల ఉత్పత్తిలో ఎక్కువ పాలు వీనినుండి లభిస్తున్నాయి.
ఎ) ఆవులు
బి) గేదెలు
సి) ఒంటెలు
డి) మేకలు, గాడిదలు
జవాబు:
ఎ) ఆవులు

ప్రశ్న 19.
ప్రొఫెసర్ జె.కె. కురియన్ ఏ విప్లవ పితామహుడు ?
ఎ) హరిత విప్లవం
బి) నీలి విప్లవం
సి) శ్వేత విప్లవం
డి) ఎల్లో రివల్యూషన్
జవాబు:
సి) శ్వేత విప్లవం

ప్రశ్న 20.
ఆపరేషన్ ప్లడ్ దీనికి సంబంధించినది.
ఎ) నూనెలు
బి) చేపలు, రొయ్యలు
సి) పాలు
డి) మాంసం, గ్రుడ్లు
జవాబు:
సి) పాలు

ప్రశ్న 21.
కంగాయం జాతి ఎద్దులు ఈ జిల్లాలో కనిపిస్తాయి.
ఎ) ఒంగోలు
బి) నెల్లూరు
సి) చిత్తూరు
డి) తూర్పుగోదావరి
జవాబు:
బి) నెల్లూరు

ప్రశ్న 22.
ఒక ఎద్దు నెలలో ఎన్ని ఆవులు గర్భం ధరించటానికి ఉపయోగపడుతుంది ?
ఎ) 10-20
బి) 20-30
సి) 10-30
డి) 1-10
జవాబు:
బి) 20-30

ప్రశ్న 23.
ఏ జాతి పశువుల పాలు ఉప్పగా ఉంటాయి ?
ఎ) ముర్రా
బి) చిల్కా
సి) కంగాయం
డి) ఒంగోలు
జవాబు:
సి) కంగాయం

ప్రశ్న 24.
మొత్తం మాంసం ఉత్పత్తిలో 74% మాంసం వీనినుండి లభిస్తుంది.
ఎ) చేపలు, రొయ్యలు
బి) గొట్టెలు, మేకలు
సి) కోళ్ళు, బాతులు
డి) ఎద్దులు
జవాబు:
డి) ఎద్దులు

ప్రశ్న 25.
ప్రపంచంలో కోడిగ్రుడ్ల ఉత్పత్తిలో భారత్ స్థానం( )
ఎ) 1
బి) 2
సి) 3
డి) 4
జవాబు:
డి) 4

ప్రశ్న 26.
ప్రపంచంలో మాంసం ఉత్పత్తిలో భారత్ స్థానం )
ఎ) 2
బి) 3
సి) 4
డి) 5
జవాబు:
బి) 3

ప్రశ్న 27.
గ్రుడ్ల కోసం పెంచే కోళ్ళు
ఎ) బ్రాయిలర్
బి) లేయర్
సి) నాటుకోళ్ళు
డి) పైవన్నీ
జవాబు:
బి) లేయర్

ప్రశ్న 28.
బ్రాయిలర్లు పెరుగుటకు పట్టే కాలం
ఎ) 5 నుండి 6 వారాలు
బి) 6 నుండి 8 వారాలు
సి) 5 నుండి 10 వారాలు
డి) 6 నుండి 12 వారాలు
జవాబు:
బి) 6 నుండి 8 వారాలు

ప్రశ్న 29.
లేయర్ కోడి వాటి జీవితకాలంలో సుమారుగా పెట్టే గ్రుడ్ల సంఖ్య
ఎ) 250-300
బి) 300-350
సి) 200-250
డి) 350-400
జవాబు:
ఎ) 250-300

ప్రశ్న 30.
గ్రుడ్లను పొదగటానికి అనుకూలమైన ఉష్ణోగ్రత
ఎ) 30°C – 31°C
బి) 33°C – 34°C
సి) 37°C – 38°C
డి) 39°C – 40°C
జవాబు:
సి) 37°C – 38°C

ప్రశ్న 31.
గ్రుడ్లను ఈ నెలలో ఎక్కువగా పొదిగిస్తారు.
ఎ) జూన్-జులై
బి) జనవరి, ఏప్రిల్
సి) ఆగస్టు-అక్టోబర్
డి) మార్చి, మే
జవాబు:
బి) జనవరి, ఏప్రిల్

ప్రశ్న 32.
N.E.C.C అనగా
ఎ) నేషనల్ ఎగ్ కో ఆర్డినేషన్ కమిటీ
బి) న్యూట్రిషనల్ ఎగ్ కో ఆర్డినేషన్ కమిటీ
సి) నాచురల్ ఎగ్ కో ఆర్డినేషన్ కమిటీ
డి) నేషనల్ ఎగ్ కన్జ్యూమర్ కమిటీ
జవాబు:
ఎ) నేషనల్ ఎగ్ కో ఆర్డినేషన్ కమిటీ

ప్రశ్న 33.
‘ఈమూ’ ఈ దేశానికి చెందిన పక్షి.
ఎ) ఆఫ్రికా
బి) ఆస్ట్రేలియా
సి) న్యూజిలాండ్
డి) అమెరికా
జవాబు:
బి) ఆస్ట్రేలియా

ప్రశ్న 34.
తేనెటీగల పెంపకాన్ని ఏమంటారు ?
ఎ) పిశికల్చర్
బి) ఎపికల్చర్
సి) పాలీ కల్చర్
డి) లాక్ కల్చర్
జవాబు:
బి) ఎపికల్చర్

ప్రశ్న 35.
అధిక తేనెనిచ్చే తేనెటీగ జాతి
ఎ) ఎపిస్ డార్సెటా
బి) ఎపిస్ ఇండికా
సి) ఎపిస్ మెల్లిఫెరా
డి) ఎపిస్ మెలిపోనా
జవాబు:
సి) ఎపిస్ మెల్లిఫెరా

ప్రశ్న 36.
భారతీయ తేనెటీగ ఒక సం||లో ఉత్పత్తి చేసే తేనెం
ఎ) 1 నుండి 3 కిలోలు
బి) 3 నుండి 5 కిలోలు
సి) 3 నుండి 8 కిలోలు
డి) 3 నుండి 10 కిలోలు
జవాబు:
డి) 3 నుండి 10 కిలోలు

ప్రశ్న 37.
యూరోపియన్ తేనెటీగ ఒక సం||రానికి ఉత్పత్తి చేసే తేనె
ఎ) 10-15 కిలోలు
బి) 15-20 కిలోలు
సి) 20-25 కిలోలు
డి) 25-30 కిలోలు
జవాబు:
డి) 25-30 కిలోలు

ప్రశ్న 38.
తేనెపట్టులో ఎన్ని రకాల ఈగలుంటాయి?
ఎ)1
బి) 2
సి) 3
డి) 4
జవాబు:
సి) 3

ప్రశ్న 39.
ఒక తేనెపట్టులో రాణి ఈగల సంఖ్య
ఎ) 1
బి) 2
సి)
డి) 4
జవాబు:
ఎ) 1

ప్రశ్న 40.
రాణి ఈగ రోజుకు పెట్టే గ్రుడ్ల సంఖ్య
ఎ) 800-1000
బి) 800-1200
సి) 800-1400
డి) 800-1600
జవాబు:
బి) 800-1200

ప్రశ్న 41.
రాణి ఈగ జీవితకాలం
ఎ) 2-3 సం||
బి) 2-4 సం||
సి) 2-5 సం||
డి) 2-6 సం||
జవాబు:
ఎ) 2-3 సం||

ప్రశ్న 42.
తేనెపట్టులో అతి తక్కువ జీవిత కాలం కలిగినవి
ఎ) రాణి
బి) డ్రోన్లు
సి) కూలీ ఈగలు
డి) ఎ మరియు బి
జవాబు:
సి) కూలీ ఈగలు

ప్రశ్న 43.
తేనెపట్టులో కూలీ ఈగలు
ఎ) వంధ్య మగ ఈగలు
బి) వంధ్య ఆడ ఈగలు
సి) ఆడ మరియు మగ ఈగలు
డి) మగ ఈగలు మాత్రమే
జవాబు:
బి) వంధ్య ఆడ ఈగలు

ప్రశ్న 44.
ఎపిస్ టింక్చరు దీనితో తయారు చేస్తారు.
ఎ) తేనె
బి) తేనెటీగల మైనం
సి) తేనెటీగల విషం
డి) అయోడిన్
జవాబు:
బి) తేనెటీగల మైనం

ప్రశ్న 45.
తేనె పట్టు నుండి తేనెను తినే జంతువు
ఎ) కోతి
బి) అడవి ఉడుత
సి) ఎలుగుబంటి
డి) గబ్బిలం
జవాబు:
సి) ఎలుగుబంటి

ప్రశ్న 46.
భారతదేశంలో సముద్రతీరం
ఎ) 6,500 కి.మీ.
బి) 7,500 కి.మీ.
సి) 8,500 కి.మీ.
డి) 9,500 కి.మీ.
జవాబు:
సి) 8,500 కి.మీ.

ప్రశ్న 47.
చేపల పెంపకంలో విత్తనం అనగా
ఎ) చేపగ్రుడ్లు
బి) చేపపిల్లలు
సి) ఎ మరియు బి
డి) గుడ్లతో ఉన్న చేపలు
జవాబు:
డి) గుడ్లతో ఉన్న చేపలు

ప్రశ్న 48.
మన సముద్ర జలాల్లో లభించే ఆర్థిక ప్రాముఖ్యత గల చేప
ఎ) బాంబేదక్
బి) ఆయిల్ సార్డెన్
సి) కాటి ఫిష్
డి) ట్యూనా
జవాబు:
సి) కాటి ఫిష్

ప్రశ్న 49.
‘ఏశ్చురీ’ అనగా
ఎ) నదీ, నదీ కలిసే ప్రదేశం
బి) నదీ, సముద్రం కలిసే ప్రదేశం
సి) కాలువ, నదీ కలిసే ప్రదేశం
డి) సముద్రం, సముద్రం కలిసే ప్రదేశం .
జవాబు:
బి) నదీ, సముద్రం కలిసే ప్రదేశం

ప్రశ్న 50.
సమ్మిళిత చేపల పెంపకంలో పరిగణనలోకి తీసుకోవల్సిన ముఖ్యమైన అంశం
ఎ) చేపల రకం
బి) చేపల ఆహారపు అలవాట్లు
సి) చేపల ఆర్థిక ప్రాముఖ్యత
డి) చేపలు పెరిగే ప్రదేశం
జవాబు:
డి) చేపలు పెరిగే ప్రదేశం

ప్రశ్న 51.
నీలి విప్లవం దీనికి సంబంధించినది.
ఎ) పాల ఉత్పత్తి
బి) మాంసం ఉత్పత్తి
సి) చేపల ఉత్పత్తి
డి) చర్మాల ఉత్పత్తి
జవాబు:
ఎ) పాల ఉత్పత్తి

ప్రశ్న 52.
పశువుల పెంపకంతో సంబంధించినది
ఎ) బయోగ్యాస్
బి) తోళ్ళ పరిశ్రమ
సి) ఎముకల పరిశ్రమ
డి) పైవన్నీ
జవాబు:
బి) తోళ్ళ పరిశ్రమ

ప్రశ్న 53.
అగార్ అగార్ అనే కలుపు మొక్కను దేని కొరకు ఉపయోగిస్తారు?
ఎ) ఆహారంగా
బి) పరిశ్రమలలో పైకో కొల్లాయిడ్ గా
సి) ఎ మరియు బి
డి) పెట్రోలియం తయారీ
జవాబు:
డి) పెట్రోలియం తయారీ

ప్రశ్న 54.
ఏ నెలలో పాల ఉత్పత్తి గరిష్ఠంగా ఉండును ?
ఎ) నవంబర్
బి) మార్చి
సి) ఆగస్టు
డి) అక్టోబర్
జవాబు:
ఎ) నవంబర్

ప్రశ్న 55.
సంక్రాంతి వంటి పండుగలలో పందేలలో పోటీపడే స్థానిక కోడి రకము
(A) చిట్టగాంగ్
(B) వైట్ లెగ్ హార్న్
(C) అసీల్
(D) బుర్నా / బెరస
జవాబు:
(C) అసీల్

ప్రశ్న 56.
మన రాష్ట్రానికి పరిమితమైన ఒక ఎండమిక్ జాతి
(A) కివి
(B) కంగారు
(C) ఒంగోలు గిత్త
(D) తెల్లపులి
జవాబు:
(C) ఒంగోలు గిత్త

ప్రశ్న 57.
తేనెటీగలు, తేనెను ఎలా తయారు చేస్తాయో తెలుసు కోవడానికి కవిత కింది ప్రశ్నలను నూరు శేషన్నది అందులో సరియైన వాటిని గుర్తించండి.
(1) తేనెటీగలలో ఎన్ని రకాలు ఉంటాయి ?
(2) పరాగసంపర్కానికి తేనెటీగలు ఎలా తోడ్పడతాయి?
(3) తేనె తయారీలో మగ ఈగల పాత్ర ఉంటుందా ?
(4) తేనెను ఈగలోని శ్వాసగ్రంథులు తయారు చేస్తాయా?
(A) 1, 2 మాత్రమే
(B) 2, 3 మాత్రమే
(C) 1 మాత్రమే
(D) 4 మాత్రమే
జవాబు:
(B) 2, 3 మాత్రమే

ప్రశ్న 58.
పశుసంవర్థనకు చెందిన సరైన నినాదం
(A) సాంప్రదాయ లేదా అధిక దిగుబడినిచ్చే పశువులలో ఏదో ఒకదానిని పెంచడం
(B) సాంప్రదాయరకాలనే పెంచడం
(C) సాంప్రదాయ లేక అధిక దిగుబడి పశువులను పెంచకపోవడం
(D) పైవన్నీ
జవాబు:
(A) సాంప్రదాయ లేదా అధిక దిగుబడినిచ్చే పశువులలో ఏదో ఒకదానిని పెంచడం

ప్రశ్న 59.
ఆక్వా కల్చర్ : చేపలు : : ఎపికల్చర్ : …..
(A) బ్రాయిలర్ కోళ్ళు
(B) రొయ్యలు
(C) పట్టుపురుగులు
(D) తేనెటీగలు
జవాబు:
(D) తేనెటీగలు

ప్రశ్న 60.
ఎపిస్ టింక్చర్ అనేది
(A) రొయ్యల
(B) కాల్షివర్ నూనె
(C) తేనెటీగల విషం నుంచి తయారీ
(D) పీతల తైలం
జవాబు:
(C) తేనెటీగల విషం నుంచి తయారీ

These AP 8th Class Biology Important Questions 4th Lesson జంతువులలో ప్రత్యుత్పత్తి will help students prepare well for the exams.

AP Board 8th Class Biology 4th Lesson Important Questions and Answers జంతువులలో ప్రత్యుత్పత్తి

ప్రశ్న 1.
కొందరు పిల్లలలో వారి తల్లిదండ్రులు లక్షణాలు రెండూ కనిపిస్తాయి – అని అనిల్ కిషోర్ తో అన్నాడు. అనిల్ మాట నిజమేనా ?
జవాబు:
అవును నిజమే. దానికి శాస్త్రీయంగా అవకాశం ఉంది.
1) తల్లి గర్భం దాల్చాలంటే తల్లి నుండి అండం – (దాని కేంద్రకంలో సగం లక్షణాలు) తండ్రి నుండి శుక్రకణం (దీని కేంద్రకంలో సగం లక్షణాలు) ఫలదీకరణ చెంది ‘సంయుక్త బీజాన్ని’ ఏర్పరుస్తాయి.
శుక్రకణం (x) + అండం (x) → సంయుక్త బీజం (2x)
50% + 50% → 100% క్రోమోజోములు
ఏకస్థితిక + ఏకస్థితిక → (ద్వయ స్థితిక)
2) అంటే సగం తండ్రి క్రోమోజోములు, సగం తల్లి క్రోమోజోములు ఉన్నాయన్న మాట.
3) ఇవి కలసి, కలగలసి, సంయుక్త బీజంలో కేంద్రకం ఏర్పడుతుందని తెలుసుకున్నారు.
4) కాబట్టి కొన్ని తల్లి వైపు నుండి గానీ, తల్లి లక్షణాలు గానీ, కొన్ని తండ్రి వైపు నుండి గానీ, తండ్రి లక్షణాలు పోలికలు గానీ పిల్లలలో వస్తాయని అనిల్, కిషోర్లు వారి మిత్రుల పోలికలు చూసి తెలుసుకున్నారు.

ప్రశ్న 2.
క్రింద ఇవ్వబడిన పుష్పంలోని పురుష స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థలలో ఉన్న భాగాలను గుర్తించుము.

జవాబు:

పురుష ప్రత్యుత్పత్తి వ్యవస్థలో భాగాలు	స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థలో భాగాలు
1) 3వ వలయం	1) 4వ వలయం
2) కేసరావళి	2) అండాశయం
3) కేసరములు	3) కీలము, కీలాగ్రం, అండాశయం
4) పుప్పొడి రేణువులు	4) అండాలు

ప్రశ్న 3.
మానవ పురుష ప్రత్యుత్పత్తి వ్యవస్థను వర్ణించండి.
జవాబు:

• మానవ పురుష ప్రత్యుత్పత్తి వ్యవస్థ ఉదరం దిగువ భాగంలో అమరి ఉంటుంది.
• పురుష ప్రత్యుత్పత్తి వ్యవస్థలో ఒక జత ముష్కాలు, ఒక జత శుక్రవాహికలు, ఒక పురుషాంగం ఉంటాయి.
• ముష్కాలు అండాకారంలో ఉంటాయి. ఇవి మిలియన్ల కొద్దీ శుక్రకణాలను ముష్కాలు ఉత్పత్తి చేస్తాయి.
• ప్రతి ముష్కం నుండి ఒక శుక్రవాహిక బయలుదేరుతుంది.
• శుక్రకణాలు శుక్రవాహికల గుండా ప్రయాణించి పురుషాంగం ద్వారా బయటకు విడుదలవుతాయి.

ప్రశ్న 4.
మానవ శుక్రకణాన్ని వర్ణించండి.
జవాబు:

• శుక్రకణాలు అతి సూక్ష్మ మైనవి.
• శుక్రకణం తల, మధ్య భాగము, పొడవైన తోకను కలిగి ఉంటుంది.
• తల భాగంలో కేంద్రకం ఉంటుంది.
• మధ్య భాగంలో అనేక మైటోకాండ్రియాలు ఉంటాయి. ఇవి శుక్ర కణాలు చలించడానికి కావలసిన శక్తిని ఉత్పత్తి చేస్తాయి.
• శుక్ర కణాలలో తోక చలనానికి తోడ్పడుతుంది.

ప్రశ్న 5.
మానవ స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థను వర్ణించండి.
జవాబు:

• స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థ ఉదరం లోపల, నాభికి కొంచెం దిగువగా అమరి ఉంటుంది.
• ఈ వ్యవస్థలో ఒక జత స్త్రీ బీజకోశాలు (Ovaries), ఒక జత ఫాలోపియన్ నాళాలు (fallopian tubes), ఒక గర్భాశయం (uterus), బాహ్య జననాంగం ఉంటాయి.
• స్త్రీ బీజకోశాలు ఉదరం లోపల, కటి భాగంలో గర్భాశయానికి ఇరువైపులా అమరి ఉంటాయి.
• ప్రతీ స్త్రీ బీజకోశం నుండి ఒక ఫాలోపియన్ నాళం బయలుదేరుతుంది.

ప్రశ్న 6.
మానవ అండాన్ని వర్ణించండి.
జవాబు:

• స్త్రీ బీజకోశాలు స్త్రీ బీజ కణాలను అంటే అండాలను ఉత్పత్తి చేస్తాయి.
• సాధారణంగా మానవులలో స్త్రీ బీజకోశం నుండి ప్రతినెలా ఒక పరిపక్వమైన అండం విడుదలవుతుంది.
• శుక్రకణం మాదిరిగా అండం కూడా ఏక స్థితిక దశలో (haploid) ఉంటుంది.
• అండం ఒక పొరతో కప్పబడి ఉంటుంది.
• అండం లోపల కణద్రవ్యంలో ఒక గుండ్రని కేంద్రకం తేలియాడుతూ ఉంటుంది.

ప్రశ్న 7.
పిండము అనగానేమి ? ఇది ఎక్కడ ఉంటుంది ?
జవాబు:

• ఫలదీకరణలో సంయుక్తబీజం ఏర్పడుతుంది.
• ఇది అనేక సార్లు విభజన చెంది అనేక కణాలను ఏర్పరుచుకుంటుంది.
• ఆ కణాలన్నీ కలిసి బంతి ఆకారాన్ని పోలి ఉంటాయి.
• ఈ కణాలే తరువాత వివిధ కణజాలాలు, అవయవాలుగా అభివృద్ధి చెందుతాయి.
• ఈ విధంగా అభివృద్ధి చెందిన నిర్మాణాన్నే ‘పిండం’ (Embryo) అంటాం.
• పిండం గర్భాశయ కుడ్యానికి అంటి పెట్టుకొని ఉంటుంది.
• పిండం యొక్క తదుపరి అభివృద్ధి గర్భాశయంలో జరుగుతుంది.

ప్రశ్న 8.
IVF అనగానేమి ? ఎటువంటి వారికి ఇది అవసరమవుతుంది ?
జవాబు:

• కొంతమంది స్త్రీలలో ఫాలోపియన్ నాళాలు మూసుకుపోయి ఉంటాయి.
• ఫలదీకరణ జరిగే అవకాశం తక్కువగా ఉంటుంది.
• అలాగే కొందరు పురుషులలో శుక్రకణాల ఉత్పత్తి, వాటి సంఖ్యలో లోపాలుంటాయి.
• కాబట్టి ఇటువంటి వ్యక్తులకు పిల్లలు పుట్టడం అరుదు.
• ఇలాంటి పరిస్థితుల్లో డాక్టర్లు సదరు వ్యక్తుల నుండి లేదా దాతల నుండి అండం సంగ్రహించి పరీక్షనాళికలో ఫలదీకరణం చెందిస్తారు. దీనినే IVF అంటాం.
• ఫలదీకరణ చెందిన సంయుక్త బీజాన్ని ఒక వారం రోజుల వరకు ప్రయోగశాలలో అభివృద్ధి చేసి తరువాత దానిని తల్లి గర్భాశయంలో ప్రవేశపెడతారు.

ప్రశ్న 9.
పవన్ పావురం పిల్లను వెంటిలేటర్ లో తిరిగి ఉంచటాన్ని ఎలా అభినందిస్తావు ? నీవు పవన్ స్థానంలో ఉంటే ఎలా ఆలోచిస్తావు ?
జవాబు:

• పవన్ పావురం పిల్లను తిరిగి వెంటిలేటర్ లో ఉంచటాన్ని మనం తప్పక అభినందించాలి.
• కారణం అతని భూతదయ మరియు జంతువుల, పక్షుల పట్ల ప్రేమ.
• అవి చిన్న పక్షులు. ఎగరలేనివి. కొంతమంది కొంటె పిల్లలు దాని నిస్సహాయతను ఆసరా చేసుకుని దాంతో ఆటలాడతారు. అందువల్ల అది చనిపోయినాపోవచ్చు.
• కానీ మన పవన్ పావురం పిల్లను చూసి, దాని లక్షణాలు గమనించి మరలా దాన్ని యథాస్థానంలో ఉంచి అభినందనీయుడయ్యాడు.
• నేను పవన్ స్థానంలో ఉన్నా ఇలానే చేసేవాడిని.
• ప్రకృతిపట్ల ప్రేమ, మన సహచర జంతు, పక్షి, వృక్షాలపట్ల భూతదయ కలిగి ఉండాలని మా సైన్స్ మాస్టారు చెప్పే మాటలను నేను తప్పక ఆచరిస్తాను.

ప్రశ్న 10.
కింది ఆధారాల సహాయంతో పదకేళిని పూర్తి చేయండి.
అడ్డం :
1. మానవునిలో జరిగే ఫలదీకరణం (9)
2. పిండం పెరుగుదల జరిగే చోటు (5)
3. అభివృద్ధి చెందిన సంయుక్త బీజం (3)
నిలువు :
1. అండం విడుదలయ్యే ప్రదేశం (5)
4. హైడ్రాలో ఉబ్బెత్తు భాగం (4)
5. అభివృద్ధి చెందిన పిండం (2)

జవాబు:

ప్రశ్న 11.
అండోత్పాదక, శిశూత్పాదక జీవులు అంటే ఏమిటి ? వాటి లక్షణాలను తెలపండి. ఉదాహరణలు ఇవ్వండి.
జవాబు:
1) గుడ్లు పెట్టి పిల్లతరాన్ని అభివృద్ధి చేసే జీవులను అండోత్పాదకాలు అంటారు. వీనిలో అంతర ఫలదీకరణ జరుగును. ఉదా : పక్షులు, సరీసృపాలు.
2) పిల్లల్ని కని పెంచి తరువాత తరాన్ని అభివృద్ధి చేసే జీవులను శిశోత్పాదక జీవులు అంటారు. ఉదా : క్షీరదాలు, గబ్బిలం.

a) అండోత్పాదక జీవిలో i) చెవులు బయటకు కనిపించవు. ii) చర్మం పై రోమాలు ఉండవు. ఇలాంటి బాహ్య లక్షణాలు ఉన్న జీవులు గుడ్లు పెడతాయి. ఉదా : పక్షులు, మొసలి,తాబేలు, పాము.
b) శిశోత్పాదక జీవిలో 1) చెవులు బయటకు కనిపిస్తాయి. ii) చర్మంపై రోమాలు ఉంటాయి. ఇలాంటి బాహ్య లక్షణాలు ఉన్న జీవులు పిల్లల్ని కని పెంచుతాయి. ఉదా : క్షీరదాలు.

ప్రశ్న 12.
క్షితిజ చేపలాంటి లార్వాను చూసి చేప అనుకొని తెచ్చి అక్వేరియంలో ఉంచింది. కొద్దిరోజుల తర్వాత ఆమె ఏం చూసి ఉంటుంది?
జవాబు:

• క్షితిజ తెచ్చిన లార్వా డిపోల్. ఇది కప్ప లార్వా.
• టాడ్ పోల్ కొన్ని రోజుల తర్వాత రూపవిక్రియ చెంది కప్పగా మారుతుంది.
• కాబట్టి క్షితిజ చేపలాంటి టాడ్ పోల్ స్థానంలో కప్పను చూసి ఉంటుంది.

ప్రశ్న 13.
టెస్ట్ ట్యూబ్ బేబీల గురించి నీకు వచ్చిన సందేహాలను తీర్చుకొనేందుకు డాక్టరును ఏమి ప్రశ్నలు అడుగుతావు ?
జవాబు:

• టెస్ట్ ట్యూబ్ బేబీలు ఎక్కడ జన్మిస్తారు ?
• టెస్ట్ ట్యూబ్ బేబీలకు సాధారణ శిశువులకు ఏ విధమైన తేడాలు ఉంటాయి ?
• ప్రజలలో టెస్ట్ ట్యూబ్ బేబీలకు ఉన్న ప్రధానమైన అపోహలు ఏమిటి ?
• టెస్ట్ ట్యూబ్ బేబీలకు ఎటువంటి ఆరోగ్య సమస్యలు ఎదురవుతాయి ?

ప్రశ్న 14.
మానవ శుక్రకణం బొమ్మను గీసి భాగాలు గుర్తించండి. కింది పట్టిక నింపండి.

వ.సం.	అవయవం	విధి
1.	తోక
2.	మైటోకాండ్రియా
3.	తల
4.	మధ్యభాగం

జవాబు:

వ.సం.	అవయవం	విధి
1.	తోక	శుక్రకణ చలనాలకు సహకరిస్తుంది.
2.	మైటోకాండ్రియా	శక్తి విడుదల చేసి శుక్రకణ కదలికలకు మరియు అండంలోకి చొచ్చుకు పోవడానికి అవసరమయ్యే శక్తిని అందిస్తుంది.
3.	తల	ఫలదీకరణంలో సహాయపడును.
4.	మధ్యభాగం	అనేక మైటోకాండ్రియాలకు స్థానం కల్పిస్తుంది.

ప్రశ్న 15.
లత మానవునిలో జరిగే ప్రత్యుత్పత్తి విధానమును తెలిపే స్లో చార్టును కింది విధంగా గీచింది. ఇది సరిఅయినదేనా ? కాకపోతే సరి చేసి రాయండి.

జవాబు:

ప్రశ్న 16.
అమీబాలో జరిగే ప్రత్యుత్పత్తి విధానం, కప్పలో జరిగే ప్రత్యుత్పత్తి విధానాల మధ్య భేదాలను రాయండి.
జవాబు:

అమీబాలో జరిగే ప్రత్యుత్పత్తి	కప్పలో జరిగే ప్రత్యుత్పతి
1. ఇది అలైంగిక ప్రత్యుత్పత్తి జరుపుతుంది.	1. ఇది లైంగిక ప్రత్యుత్పత్తి జరుపుతుంది.
2. సంయోగబీజాల కలయిక ఉండదు.	2. సంయోగ బీజాల కలయిక ఉంటుంది.
3. ద్విధావిచ్చిత్తి లేదా బహుధా విచ్చితి జరిపి పిల్ల అమీబాలు ఏర్పడుతాయి.	3. బాహ్య ఫలదీకరణ ప్రక్రియలో అనేక జీవులు జన్మిస్తాయి.
4. ఏర్పడిన పిల్ల అమీబాలు పూర్తిగా తల్లిని పోలి ఉంటాయి.	4. ఏర్పడిన జీవులు రూపంలో వైవిధ్యాన్ని ప్రదర్శిస్తాయి.
5. ప్రత్యుత్పత్తి తరువాత తల్లి జీవి అంతరించి పోతుంది.	5. ప్రత్యుత్పత్తి అనంతరం తల్లి జీవి అంతరించదు.

ప్రశ్న 17.
కప్ప జీవితచరిత్రను పరిశీలించేందుకు చేసిన ప్రాజెక్టులో నీవు ఏయే పరికరాలను ఉపయోగించావు ?
జవాబు:
వెడల్పు మూతి గల తొట్టి లేక గాజు సీసా, పారదర్శక గ్లాస్, డ్రాపర్, పెట్రేడిష్, గులకరాళ్ళు, భూతద్దం, బీకరు.

ప్రశ్న 18.
కింది పేరా చదివి ఖాళీలను వివరించండి.
పురుషులలో వుండే ప్రధాన ప్రత్యుత్పత్తి అవయవాలు A మరియు స్త్రీలలో వుండే ప్రధాన ప్రత్యుత్పత్తి అవయవాలు B. A మరియు B లు C, D అనే బీజకణాలను విడుదల చేస్తాయి. C, D ల కలయికను E అంటారు. E ఫలితంగా F ఏర్పడుతుంది. F క్రమేపి పెరిగి G గా ఏర్పడి చివరకు H గా మారుతుంది.

ప్రశ్న 19.
కింది పటాన్ని పరిశీలించండి. ప్రశ్నలకు జవాబులు రాయండి.

1. ఈ పటం ఏ వ్యవస్థకు చెందినది.
జవాబు:
మానవ పురుష ప్రత్యుత్పత్తి వ్యవస్థ

2. ఇందులో A, B, C భాగాలను గుర్తించండి.
జవాబు:
A – శుక్రవాహికలు
B – ముష్కాలు
C – పురుషాంగం

3. B భాగము నుండి ఏమి ఉత్పత్తి అవుతాయి ?
జవాబు:
శుక్రకణాలు

4. భాగము A యొక్క పని ఏమిటి ?
జవాబు:
శుక్రవాహికల గుండా శుక్రకణాలు ప్రయాణించి పురుషాంగం ద్వారా బయటకు విడుదల అవుతాయి.

ప్రశ్న 20.
కింది చిత్రాన్ని పరిశీలించి ప్రశ్నలకు సమాధానాలు రాయండి.

1. ఇది ఏ వ్యవస్థకు చెందినది ?
జవాబు:
ఇది మానవ స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థ

2. A భాగం పేరేమి ఇక్కడ ఏమి ఉత్పత్తి అవుతాయి ?
జవాబు:
స్త్రీ బీజకోశం

3. B భాగం పేరేమి ?
జవాబు:
గర్భాశయం

4. ఫాలోపియన్ నాళాలు మూసుకొనిపోతే ఏమౌతుంది ?
జవాబు:
ఫలదీకరణం జరుగదు.

1 మార్కు ప్రశ్నలు

ప్రశ్న 1.
అన్ని జంతువులు గుడ్లు పెడతాయా ?
జవాబు:
లేదు. చేపలు, ఉభయచరాలు, సరీసృపాలు, పక్షులు మాత్రమే గుడ్లు పెడతాయి. క్షీరదాలు గుడ్లు పెట్టవు. పిల్లల్ని కంటాయి.

ప్రశ్న 2.
ఏ ఏ జంతువులు పిల్లల్ని కంటాయి ?
జవాబు:
క్షీరదాలు అన్ని పిల్లల్ని కంటాయి. ఉదా : ఆవు, గేదె, గుర్రం, ఎలుక, పిల్లి, ఏనుగు, మనిషి.

ప్రశ్న 3.
ఏ ఏ జంతువులు గ్రుడ్లు పెడతాయో, ఏవి పిల్లల్ని కంటాయో తెలుసుకోవటం ఎలా ?
జవాబు:
పిల్లల్ని కనే జంతువులలో కొన్ని బాహ్య లక్షణాలు విభిన్నంగా ఉంటాయి. వీటి ఆధారంగా పిల్లల్ని కనే జంతువులను గుడ్లు పెట్టే వాటి నుండి వేరుగా తెలుసుకోవచ్చు.

ప్రశ్న 4.
పిల్లల్ని కనే జంతువుల బాహ్య లక్షణాలు తెలుసుకోవడానికి పద్ధతులేమైనా ఉన్నాయా ?
జవాబు:
పిల్లల్ని కనే జంతువులు బాహ్య చెవులను, చర్మం మీద రోమాలను కలిగి ఉంటాయి. వీటి ఆధారంగా పిల్లల్ని కనే జంతువులను గుర్తించవచ్చు.

ప్రశ్న 5.
శుక్రకణం అండంతో ఫలదీకరణ చెందకపోతే ఏమవుతుందో చెప్పగలరా ?
జవాబు:
శుక్రకణం అండంతో ఫలదీకరణ చెందకపోతే లైంగిక ప్రత్యుత్పత్తి జరగదు. వైవిధ్యం గల జీవులు ఏర్పడవు. క్రొత్త జాతులు అవతరించవు.

ప్రశ్న 6.
కొన్ని జంతువులు మాత్రమే పిల్లలకు ఎందుకు జన్మనిస్తాయో చెప్పగలరా ?
జవాబు:
పిల్లల్ని కనే స్త్రీ జంతువుల్లో గర్భాశయము, పిండాభివృద్ధికి అనుకూలంగా ఉంటుంది. అందువలన పిండాలు గర్భాశయంలో ఎదిగి పిల్ల జీవులుగా పుడతాయి. గుడ్లు పెట్టే జంతువులలో ఈ అమరిక ఉండదు.

ప్రశ్న 7.
జంతువులన్నీ పిల్లలకు జన్మనివ్వడం ఆపివేస్తే ఏం జరుగుతుంది ?
జవాబు:
జంతువులన్నీ పిల్లలకు జన్మనివ్వడం ఆపివేస్తే, తదుపరి తరం జీవులు ఉత్పత్తి కావు. ఉన్న జీవులు కొంత కాలానికి మరణిస్తాయి. కావున భూమి మీద జీవరాశి అంతరించిపోతుంది.

ప్రశ్న 8.
టాడిపోల్ ఏ ఆకారాన్ని పోలి ఉంది ?
జవాబు:
టాడి పోల్ చేప ఆకారాన్ని పోలి ఉంది.

ప్రశ్న 9.
ఏ దశలో టాడ్ పోల్ లో మొప్పలు కనిపిస్తాయి ?
జవాబు:
గుడ్డు నుండి వచ్చిన టాడ్పేల్ బాహ్య మొప్పలు కలిగి ఉంది. మొదటి దశలో టాడ్ పోల్ లార్వా బాహ్య మొప్పలు కలిగి ఉంది.

లక్ష్యాత్మక నియోజనము

సరియైన సమాధానమును గుర్తించుము.

ప్రశ్న 1.
పుష్పంలో పురుష ప్రత్యుత్పత్తి వ్యవస్థ
ఎ) కీలం
బి) కేసరావళి
సి) అండాశయం
డి) ఆకర్షక పత్రాలు
జవాబు:
బి) కేసరావళి

ప్రశ్న 2.
శుక్రకణం + అండం = ………….
ఎ) సంయుక్త బీజము
బి) కోరకం
సి) భ్రూణం
డి) పిల్లకణం
జవాబు:
ఎ) సంయుక్త బీజము

ప్రశ్న 3.
రూపవిక్రియ …………. లో జరుగును.
ఎ) మానవుడు
బి) ఒంటె
సి) కప్ప
డి) పాము
జవాబు:
సి) కప్ప

ప్రశ్న 4.
బాహ్య ఫలదీకరణం …….. లో జరుగును.
ఎ) చేప
బి) ఈగ
సి) పిల్లి
డి) ఎలుక
జవాబు:
ఎ) చేప

ప్రశ్న 5.
అంతర ఫలదీకరణ ……….. లో జరుగును.
ఎ) చేప
బి) కప్ప
సి) వానపాము
డి) మానవుడు
జవాబు:
డి) మానవుడు

ప్రశ్న 6.
శుక్రకణం జీవితకాలం …… గం॥
ఎ) 24
బి) 34
సి) 36
డి) 38
జవాబు:
ఎ) 24

ప్రశ్న 7.
గర్భాశయం …….. భాగంలో ఉంటుంది.
ఎ) పొట్ట
బి) పొత్తి కడుపు
సి) ఛాతి
డి) మెడ
జవాబు:
బి) పొత్తి కడుపు

ప్రశ్న 8.
పట్టు పురుగు ………. ఆకులను మాత్రమే తింటుంది.
ఎ) మందార
బి) మునగ
సి) మల్బరీ
డి) మామిడి
జవాబు:
సి) మల్బరీ

ప్రశ్న 9.
మానవునిలో గర్భావధి కాలం …… రోజులు.
ఎ) 270-280
బి) 280-290
సి) 290-300
డి) 300-310
జవాబు:
ఎ) 270-280

ప్రశ్న 10.
…….. కాలంలో కప్పలు ఫలదీకరణంలో పాల్గొంటాయి.
ఎ) ఎండాకాలం
బి) వర్షాకాలం
సి) శీతాకాలం
డి) వసంతకాలం
జవాబు:
బి) వర్షాకాలం

ప్రశ్న 11.
ఒక జంతువు గ్రుడ్డు పెడుతుందా, లేదా పిల్లల్ని కంటుందా అని దీనిని చూసి చెప్పవచ్చు.
ఎ) చెవి
బి) రోమాలు
సి) ఎ మరియు బి
డి) చెప్పలేము
జవాబు:
సి) ఎ మరియు బి

ప్రశ్న 12.
పిల్లల్ని కనే జంతువుల్ని ఏమంటారు ?
ఎ) అండోత్పాదకాలు
బి) శిశోత్పాదకాలు
సి) పిండోత్పాదకాలు
డి) పైవేవీ కావు
జవాబు:
బి) శిశోత్పాదకాలు

ప్రశ్న 13.
సంయోగబీజాలు ఏర్పడకుండా కొత్తతరాన్ని ఏర్పరిచే పద్దతి
ఎ) అలైంగిక ప్రత్యుత్పత్తి
బి) లైంగిక ప్రత్యుత్పత్తి
సి) భిన్నోత్పత్తి
డి) పిండోత్పత్తి
జవాబు:
ఎ) అలైంగిక ప్రత్యుత్పత్తి

ప్రశ్న 14.
అలైంగిక ప్రత్యుత్పత్తి జరపని జీవి
ఎ) అమీబా
బి) పేరమీషియం
సి) హైడ్రా
డి) వానపాము
జవాబు:
డి) వానపాము

ప్రశ్న 15.
హైడ్రాలో జరిగే అలైంగిక ప్రత్యుత్పత్తి
ఎ) ద్విధావిచ్ఛిత్తి
బి) కోరకీభవనం
సి) బహుధా విచ్ఛిత్తి
డి) సిద్ధబీజాలు
జవాబు:
బి) కోరకీభవనం

ప్రశ్న 16.
అమీబాలో జరిగే అలైంగిక ప్రత్యుత్పత్తి
ఎ) ద్విధావిచ్ఛిత్తి
బి) కోరకీభవనం
సి) బహుధావిచ్ఛిత్తి
డి) సిద్ధబీజాలు
జవాబు:
ఎ) ద్విధావిచ్ఛిత్తి

ప్రశ్న 17.
ద్విదావిచ్ఛిత్తిలో ఒక అమీబా నుండి ఎన్ని పిల్ల అమీబాలేర్పడతాయి ?
ఎ) 1
బి) 2
సి) 3
డి) 4
జవాబు:
బి) 2

ప్రశ్న 18.
స్త్రీ, పురుష సంయోగబీజాల కలయిక ద్వారా ఏర్పడేది
ఎ) అండం
బి) పిండం
సి) సంయుక్తబీజం
డి) సిద్ధబీజం
జవాబు:
సి) సంయుక్తబీజం

ప్రశ్న 19.
శుక్రకణం చలించటానికి కావలసిన శక్తి యిక్కడ ఉత్పత్తి అవుతుంది.
ఎ) తల
బి) మధ్యభాగం
సి) తోక
డి) శుక్రకణం మొత్తం
జవాబు:
బి) మధ్యభాగం

ప్రశ్న 20.
శుక్రకణంలో మైటోకాండ్రియాలు ఉండే ప్రదేశం
ఎ) తల
బి) మధ్యభాగం
సి) తోక
డి) ఎ మరియు బి
జవాబు:
బి) మధ్యభాగం

ప్రశ్న 21.
ముష్కాలుండునది
ఎ) పురుష ప్రత్యుత్పత్తి వ్యవస్థ
బి) స్త్రీ ప్రత్యుత్పత్తి వ్యవస్థ
సి) స్త్రీ పిండాభివృద్ధి వ్యవస్థ
డి) గర్భాశయం
జవాబు:
ఎ) పురుష ప్రత్యుత్పత్తి వ్యవస్థ

ప్రశ్న 22.
ఒక స్త్రీ బీజకోశం నుండి అండం విడుదలయ్యేది
ఎ) నెలకు ఒకటి
బి) నెలకు రెండు
సి) రెండు నెలలకి ఒకటి
డి) రెండు నెలలకు రెండు
జవాబు:
సి) రెండు నెలలకి ఒకటి

ప్రశ్న 23.
ఈ క్రింది వానిలో ద్వయ స్థితికంలో ఉండునది
ఎ) శుక్రకణం
బి) అండం
సి) సంయుక్తబీజం
డి) అంకురచ్ఛదం
జవాబు:
సి) సంయుక్తబీజం

ప్రశ్న 24.
ఈ క్రింది వానిలో బాహ్యఫలదీకరణం జరిగే జీవి
ఎ) కప్ప
బి) పాము
సి) బల్లి
డి) కోడి
జవాబు:
ఎ) కప్ప

ప్రశ్న 25.
సంయుక్తబీజం భ్రూణంగా మార్పుచెందే ప్రక్రియ నేమంటారు ?
ఎ) ఫలదీకరణం
బి) గర్భం దాల్చుట
సి) శిశు జననం డ
డి) గర్భావధి కాలం
జవాబు:
బి) గర్భం దాల్చుట

ప్రశ్న 26.
పూర్తిగా అభివృద్ధి చెందిన పిండాన్ని ఏమంటారు ?
ఎ) అండం
బి) పిండం
సి) భ్రూణం
డి) శిశువు
జవాబు:
సి) భ్రూణం

ప్రశ్న 27.
టెస్ట్యూబ్ బేబిలో పిండాభివృద్ధి యిక్కడ జరుగుతుంది.
ఎ) పరీక్షనాళిక
బి) తల్లి గర్భాశయం
సి) కృత్రిమ గర్భాశయం
డి) తండ్రిలో ప్రత్యేక సంచి
జవాబు:
బి) తల్లి గర్భాశయం

ప్రశ్న 28.
IVF అనగా
ఎ) ఇ విట్రో ఫెర్టిలైజేషన్
బి) ఇంట్రా వర్టికల్ ఫెర్టిలైజేషన్
సి) ఇన్వర్టికల్ ఫాలోపియస్ట్యూబ్
డి) ఇన్వర్టికల్ ఫెర్టిలైజేషన్
జవాబు:
ఎ) ఇ విట్రో ఫెర్టిలైజేషన్

ప్రశ్న 29.
రూపవిక్రియ చూపని జీవి
ఎ) వానపాము
బి) కప్ప
సి) పట్టుపురుగు
డి) సీతాకోకచిలుక
జవాబు:
ఎ) వానపాము

ప్రశ్న 30.
ఈ క్రింది వానిలో ఉభయ లైంగిక జీవి
ఎ) వానపాము
బి) కప్ప
సి) చేప
డి) బొద్దింక
జవాబు:
ఎ) వానపాము

ప్రశ్న 31.
కప్ప లార్వానేమంటారు ?
ఎ) రిగ్లర్
బి) టంబ్లర్
సి) టాడ్పేల్
డి) మాగట్
జవాబు:
సి) టాడ్పేల్

ప్రశ్న 32.
క్లోనింగ్ ప్రక్రియను మొదటిసారిగా నిర్వహించినది
ఎ) జూలీ రాబర్ట్
బి) ఇయాన్ విల్మట్
సి) ఆడమ్
డి) విల్సన్
జవాబు:
బి) ఇయాన్ విల్మట్

ప్రశ్న 33.
క్లోనింగ్ ప్రక్రియను ఈ జీవిపై చేశారు.
ఎ) ఎలుక
బి) కోతి
సి) కుందేలు
డి) గొర్రె
జవాబు:
డి) గొర్రె

ప్రశ్న 34.
క్లోనింగ్ ప్రక్రియలో జన్మించిన గొర్రె పేరు
ఎ) బాలి
బి) డాలి
సి) జూలి
డి) డోలి
జవాబు:
బి) డాలి

ప్రశ్న 35.
జంతువుల క్లోనింగను మొదటిసారిగా విజయవంతంగా జరిపిన శాస్త్రవేత్త
ఎ) బ్యారి మార్గాల్
బి) ఇయాన్ విల్మట్
సి) ఎ.జి.టాన్స్ లే
డి) ఎడ్వర్డ్ జెన్నర్
జవాబు:
బి) ఇయాన్ విల్మట్

ప్రశ్న 36.
మనదేశంలో చట్టపరంగా పురుష, స్త్రీ వివాహ వయసు
ఎ) 18, 21
బి) 19, 21
సి) 21, 19
డి) 21, 18
జవాబు:
డి) 21, 18

ప్రశ్న 37.
ఈ క్రింది ప్రత్యుత్పత్తి విధానంలో సంయోగబీజదాలు ఏర్పడవు. ఇందుకు ఉదాహరణ
ఎ) లైంగిక ప్రత్యుత్పత్తి-మానవుడు
బి) అలైంగిక ప్రత్యుత్పత్తి-హైడ్రా
సి) లైంగిక ప్రత్యుత్పత్తి-కప్ప
డి) లైంగిక ప్రత్యుత్పత్తి-కోడి
జవాబు:
బి) అలైంగిక ప్రత్యుత్పత్తి-హైడ్రా

ప్రశ్న 38.
సంయుక్తబీజం పదేపదే విభజనచెంది అభివృద్ధి చెందేది
ఎ) పిల్లలు
బి) పిండము
సి) భ్రూణము
డి) అండము
జవాబు:
బి) పిండము

ప్రశ్న 39.
సరికాని దానిని గుర్తించండి.
ఎ) హైడ్రా – ద్విధావిచ్ఛిత్తి
బి) మానవుడు – అంతర ఫలదీకరణ
సి) చేపలు – బాహ్య ఫలదీకరణ
డి) పక్షులు – అంతర ఫలదీకరణ
జవాబు:
ఎ) హైడ్రా – ద్విధావిచ్ఛిత్తి

ప్రశ్న 40.
సంయుక్త బీజం, భ్రూణముగా ఎదగడానికి పట్టే కాలాన్ని ‘గర్భావధి కాలం’ అంటారు. మానవులలో ఇది
ఎ) 120 – 180 రో॥
బి) 270 – 280 రో॥
సి) 310 – 320 రో॥
డి) 180 – 220 రో॥
జవాబు:
బి) 270 – 280 రో॥

ప్రశ్న 41.
కింది వానిలో బాహ్యఫలధీకరణం జరుపుకునే జీవులు
ఎ) చేప, కప్ప
బి) కాకి, కోడి
సి) గేదె, ఆవు
డి) పాము, ఉడుత
జవాబు:
ఎ) చేప, కప్ప

ప్రశ్న 42.
మగ పుష్పంలో లోపించిన భాగం
ఎ) రక్షక పత్రావళి
బి) ఆకర్షణ పత్రావళి
సి) కేసరం
డి) కీలాగ్రం
జవాబు:
డి) కీలాగ్రం

ప్రశ్న 43.
కింది వానిలో అండోత్పాదకాలను గుర్తించండి.
1) గేదె
2) చిలుక
3) చేప
4) ఆవు
5) కప్ప
6) జింక
ఎ) 1, 4, 6
బి) 1, 2, 6
సి) 2, 3, 5
డి) 5, 2, 1
జవాబు:
సి) 2, 3, 5