Mahesh

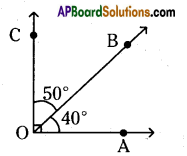
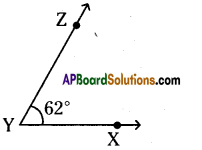
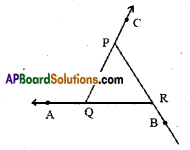
AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Ex 10.1

Question 1.
Construct a line segment of length 6.9 cms using ruler and compass.

Solution:
Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compass on the zero mark of the ruler. Open the compass, so that pencil point touches the 6.9 cm mark on the ruler.
3. Place the pointer at A on the line l and draw an arc to cut the line. Mark the point where the arc cuts the line as B
4. On the line l, we got the line segment AB of required length.
   

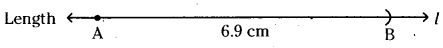
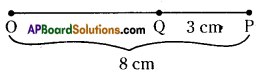
Question 2.
Construct a line segment of length 4.3 cms using ruler.
Solution:

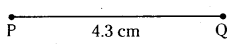
Steps of construction:

1. Place the ruler on paper and hold it firmly.
2. Mark a point with a sharp edged pencil against 0 cm mark on the ruler. Name the point as P.
3. Mark another point against 3 small divisions just after the 4 cm mark. Name this point as Q.
4. Join points P and Q along the edge of the ruler.
   Therefore, PQ is the required line segment of length 4.3 cm.

Question 3.
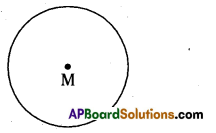
Construct a circle with centre M and radius 4 cm.
Solution:

Steps of construction:

1. Mark a point M on the paper.
2. By using compasses take 4 cm as the radius on with the scale.
3. Place the metal point on M and draw a circle from M.
   Hence required circle is constructed with center M and radius 4 cm.

Question 4.
Draw any circle and mark three points A, B and C such that
(i) A is on the circle
(ii) B is in the interior of the circle
(iii) C is in
Solution:

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Unit Exercise

Question 1.
Give examples for each shape in the table.

Sphere	Cylinder	Cube	Cone
1.
2.
3.	.

Solution:

Sphere	Cylinder	Cube	Cone
1. Marbles	Chalk piece	Dice	Heap of rice
2. Laddu	Road roller	Ice cube	Tent
3. Tennis ball	Pillar of building	Rubic cube	Joker cap

Question 2.
Look at the adjacent figure and answer the following questions,
(i) What is the name of the triangle?
(ii) Write all sides, angles and vertices of the triangle.
Solution:
i) Name of the given triangle is ΔPQR.
ii) The sides of ΔPQR are [latex]\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}[/latex] and [latex]\overline{\mathrm{PR}}[/latex] .
The angles of ΔPQR are ∠P, ∠Q and ∠R.
The vertices of ΔPQR are P, Q and R.

Question 3.
Look at the adjacent figure and answer the following questions.
(i) Write the name of this polygon.
(ii) Write the pairs of adjacent sides and adjacent angles.
(iii) Write all vertices, pairs of opposite sides and pairs of opposite angles.
Solution:
i) Name of the given polygon is quadrilateral EFGH.
ii) EH and FG are pair of adjacent sides of EF.
EF’ and GH are pair of adjacent sides of FG.
FG and EH are pair of adjacent sides of GH.
EF and HG are pair of adjacent sides of EH.
Adjacent angles of E are ∠H and ∠F.
Adjacent angles of F are ∠E and ∠G.
Adjacent angles of G are ∠F and ∠H.
Adjacent angles of H are ∠G and ∠E

iii)Vertices of the quadrilateral EFGH are E, F, G and H.
Opposite side of EF is GH.
Opposite side of FG is EH.
Pairs of opposite angles are ∠E, ∠G and ∠F, ∠H.

Question 4.
Say true or false.
(i) We can locate only one centre in a circle. [ ]
(ii) All chords are called diameters. [ ]
(iii) A square pyramid has squares as its faces. [ ]
Solution:
i) True
ii) False
iii) False

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.4

Question 1.
Write the shapes of the following.
(i) A brick (ii) A road roller (iii) Foot ball (iv) Joker cap
Solution:
i) Shape of a brick is cuboid.
ii) Shape of a road roller is cylinder.
iii) Shape of a foot ball is shpere.
iv) Shape of a joker cap is cone.

Question 2.
Fill in the blanks.
(i) The shape of heap of grain
(ii) The shape of a dice
(iii) The shape of a bubble
(iv) The shape of a candle
Solution:
i) Cone ii) Cube iii) Sphere

Question 3.
Match the following.

Solution:

Question 4.
Fill in the table.

Shape	No.of faces	No. of vertices	No. of edges
Cube
Triangular prism
Square pyramid
Cuboid

Verify Euler’s Formula for the data in the table.

We know that, the F + V = E + 2is Euler’s formula.
In the above table given shapes satisfy the Euler’s formula.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.3

Question 1.
Look at the given quadrilateral and answer the following questions.
i) What are the sides of the given quadrilateral?
ii) What is the opposite side of [latex]\overline{\mathrm{AB}}[/latex] ?
iii) What is the opposite vertex of B?
iv) What is the opposite angle of ∠C ?
v) How many pairs of adjacent angles are there? What are they?
vi) How many pairs of opposite angles are there? What are they?

Solution:
In the given quadrilateral ABCD,
i) It has four sides. They are [latex]\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}} \text { and } \overline{\mathrm{AD}}[/latex]
ii) Opposite side of [latex]\overline{\mathrm{AB}}[/latex] is [latex]\overline{\mathrm{DC}}[/latex]
iii) Opposite vertex to B is D.
iv) Opposite angle of ∠C is ∠BAD (or) ∠A.
v) It has four pair of adjacent angles are there. They are :
Adjacent angles of ∠A are ∠B and ∠D.
Adjacent angles of ∠B are ∠A and ∠C.
Adjacent angles of ∠C are ∠B and ∠D.
Adjacent angles of ∠D are ∠A and ∠C.
vi) It has two pairs of opposite angles are there. They are ∠A and ∠C; ∠B and ∠D.

Question 2.
Find the number of lines of symmetry in the following.

Solution:
i) Given adjacent figure is a square.
Number of lines of symmetry to a square are 4

ii) Given adjacent figure is a circle.
Number of lines of symmetry to a circle are infinite (many).

iii) Given adjacent figure is a triangle.
Number of lines of symmetry to the triangle are three.
(If it is an equilateral triangle).

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.2

Question 1.
Look at the given triangle and answer the following questions.
i) Which points are marked in the exterior of the triangle?
ii) Which points are marked on the triangle?
iii) Which points are marked in the interior of the triangle?

Solution:
i) The points marked in the exterior of the triangle are X, Y and Z.
ii) The points marked on the triangle are A, I, B, J and C.
iii) The points marked in the interior of the triangle are K, L and O.

Question 2.
Look at the adjacent figure. Answer the following questions.
i) How many sides are there in the triangle? What are they?
ii) How many vertices lie there on the triangle? What are they?
iii) What is the side opposite to the vertex P?
iv) What is the vertex opposite to [latex]\overline{\mathrm{PR}}[/latex] ?

Solution:
In the given ∆PQR,
i) It has three sides. They are [latex]\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}[/latex] and [latex]\overline{\mathrm{PR}}[/latex]
ii) It has three vertices. They are P, Q and R.
iii) The side opposite to the vertex P is [latex]\overline{\mathrm{QR}}
iv) The vertex opposite to the side [latex]\overline{\mathrm{PR}}[/latex] is Q.

Question 3.
Look at the given triangle and answer the following questions.
i) How many angles are there in the triangle? What are they?
ii) What is the angle opposite to [latex]\overline{\mathrm{MN}}[/latex] ?
iii) Where is the right angle in the given triangle ?

Solution:
In the given ∆MON,
i) It has three angles, they are ∠MNO, ∠NOM and ∠OMN.
ii) Angle opposite to the side [latex]\overline{\mathrm{MN}}[/latex] is ∠MON or ∠O.
iii) In the triangle ∠MON is the right angle.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.1

Question 1.
What is the name of four sided polygon? Draw the rough sketch.
Solution:
A four sided polygon is called a quadrilateral.

ABCD is a quadrilateral.

Question 2.
Draw a rough sketch of pentagon.
Solution:
A five sided polygon is called a pentagon.
So, pentagon has five sided figure.

ABCDE is a pentagon.

Question 3.
Write all the sides of the given polygon ABCDEF.
Solution:
Given polygon ABCDEF is a Hexagon.
Its six sides are [latex]\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DE}}, \overline{\mathrm{EF}} \text { and } \overline{\mathrm{FA}}[/latex]
So, it is called a Hexagon.

Question 4.
Write the interior angles of the polygon PQRST.
Solution:
Given the polygon PQRST has five sides.
So, it is called a Pentagon.
It has five interior angles.
They are ∠TPQ, ∠PQR, ∠QRS, ∠RST and ∠STP.
They can also be written as ∠P, ∠Q, ∠R, ∠S, ∠T.

Question 5.
Measure the length of the sides of the polygon PQRST.
Solution:
The given polygon has five sides.
They are [latex]\overline{\mathrm{PQ}}[/latex] = 2cm; [latex]\overline{\mathrm{QR}}[/latex] = 2.5 cm;
[latex]\overline{\mathrm{RS}}[/latex] .= 2.4 cm; [latex]\overline{\mathrm{ST}}[/latex] = 2.2 cm, [latex]\overline{\mathrm{PT}}[/latex] = 2.5 cm
It’s a pentagon.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Unit Exercise

Question 1.
In the given figure, measure the length of AC. Check whether
i) AB + AC > AC
ii) AC > AD – DC
Solution:
In the given figure, AB = 4.2 cm; BC = 5.5 cm
AC = 5.4 cm; CD = 3 cm; AD = 4 cm.
i) AB + AC = 4.2 + 5.4 = 9.6 cm > 5.4 cm
AB + AC > AC
ii) AD – DC = 4 – 3 = 1 cm < 5.4 cm
AD – DC < AC (or) AC > AD – DC

Question 2.
Draw a line segment [latex]\overline{\mathbf{A B}}[/latex]. Put a point C in between [latex]\overline{\mathbf{A B}}[/latex]. Extend [latex]\overline{\mathbf{C B}}[/latex] upio D such that CD > AB. Now check whether AC and BD are equal length.
Solution:

Let draw a line [latex]\overline{\mathbf{A B}}[/latex] = 5 cm and mark a point C on [latex]\overline{\mathbf{A B}}[/latex] such that [latex]\overline{\mathbf{A C}}[/latex] = 3 cm (or) [latex]\overline{\mathbf{BC}}[/latex] = 2 cm Extend [latex]\overline{\mathbf{C B}}[/latex] up to D such that [latex]\overline{\mathbf{C D}}[/latex] = 5 cm ([latex]\overline{\mathbf{C B}}[/latex] = 2 cm, [latex]\overline{\mathbf{B D}}[/latex] = 3 cm)
∴ [latex]\overline{\mathbf{A C}}[/latex] = 3cm, [latex]\overline{\mathbf{C B}}[/latex] = 2cm, [latex]\overline{\mathbf{B D}}[/latex] = 3cm
∴ [latex]\overline{\mathrm{AC}}=\overline{\mathrm{BD}}[/latex] = 3cm.

Question 3.
Draw an angle ∠AOB as m∠AOB = 40°. Draw an angle ∠BOC such that ∠AOC = 90°
Check whether m∠AOB + m∠BOC = m∠AOC.
Sol. Draw an angle ∠AOB = 40° and ∠AOC = 90° on the same ray [latex]\overrightarrow{\mathrm{OA}}[/latex]
Now, measure ∠AOB = 40° and ∠BOC = 50°
∴ m∠AOB + m∠BOC = 40° + 50 = 90°
m∠AOB + m∠BOC = 90° = m∠AOC
∴ m∠AOB + m∠BOC = m∠AOC.

Question 4.
Draw an angle ∠XYZ as m∠XYZ = 62°. Measure the exterior angle ∠XYZ.
Solution:

Draw angle ∠XYZ = 62° (Interior)
Now, measure the exterior angle ∠XYZ.
∴ Exterior angle of ∠XYZ = 298°

Question 5.
Match the following.
1. Set square — A) to measure angles
2. Protractor — B) to measure the lengths of line segments
3. Divider — C) to draw parallel lines
Sol. 1) Set square — C) to draw parallel lines
2) Protractor — A) to measure angles
3) Divider — B) to measure the lengths of line segments

Question 6.
List out the letters of English alphabet (capital letters) which consist of right angles.
Solution:
The letters which consists of right angles in English alphabet are

Question 7.
Measure the angles ∠AQP, ∠CPR, ∠BRQ.

Find m∠AQP, m∠CPR, m∠BRQ.
Solution:
In the given figure, measure the angles ∠AQR, ∠CPR, ∠BRQ
∠AQP = 120°
∠CPR = 120°
and ∠BRQ = 120°
∴ m∠AQP = 120°; m∠CPR = 120°; m∠BRQ = 120°

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.4

Question 1.

Measure all the angles in the above figures.

∠1 = 70°
∠3 = 70°
∠5 = 70°
∠7 = 70°

∠2 = 110°
∠4 = 110°
∠6 = 110°
∠8= 110°

∠a = 60°
∠c = 60°
∠e = 50°
∠g = 50°

∠b = 120°
∠d = 120°
∠f = 130°
∠h = 130°

Question 2.
Sum of which two angles is 180° in each figure ?
Solution:
From above question,
i) ∠1 + ∠2 = 180°

i) ∠1 + ∠2 = 180°
∠2 + ∠3 = 180°
∠1 + ∠4 = 180°
∠3 + ∠4 = 180°

∠5 + ∠6 = 180°
∠6 + ∠7 = 180°
∠7 + ∠8 = 180°
∠5 + ∠8 = 180°

∠1 + ∠8 = 180°
∠4 + ∠5 = 180°
∠2 + ∠7 = 180°
∠3 + ∠6 = 180°

ii) ∠a + ∠b = 180°
∠b + ∠c = 180°
∠c + ∠d = 180°
∠a + ∠d = 180°

∠e + ∠f = 180°
∠f + ∠g = 180°
∠g + ∠h = 180°
∠e + ∠h = 180°

Question 3.
In the given figure measure ∠FOG and draw the same in your note book.

Solution:

Question 4.
In the given figure measure the angles ∠AOB, ∠BOC.

Solution:

∠AOB = 110°
∠BOC = 60°
∠AOC = 50°

Question 5.
Write some acute, obtuse and reflexive angles atleast 2 for each.
Solution:
Acute angles : 10°, 30°, 45°, 60°, 89° (< 90°)
Obtuse angles : 110°, 150°, 160°, 172°, 178° (90° < obtuse < 180°) Reflex angles : 210°, 270°, 300°, 345°, 359° (reflex > 180°)

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.3

Question 1.
Given ” [latex]\overline{\mathrm{AB}} / / \overline{\mathrm{CD}}[/latex], l ⊥ m”. Which are perpendicular? Which are parallel?
Solution:
are parallel lines (// is the symbol for parallel),
l, m are perpendicular lines (⊥ is the symbol for perpendicular).

Question 2.
Write the set of parallels and perpendiculars in the given by using symbols.

Solution:
a) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{DC}}[/latex] are parallel lines, we denote this by writing [latex]\overline{\mathrm{AB}} / / \overline{\mathrm{DC}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[/latex] is parallel to [latex]\overline{\mathrm{DC}}[/latex]
b) [latex]\overline{\mathrm{AD}}, \overline{\mathrm{BC}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{AD}} / / \overline{\mathrm{BC}}[/latex] and can be read as [latex]\overline{\mathrm{AD}}[/latex] is parallel to [latex]\overline{\mathrm{BC}}[/latex]
c) [latex]\overline{\mathrm{AQ}}, \overline{\mathrm{PC}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{AQ}} / / \overline{\mathrm{PC}}[/latex] and can be read as [latex]\overline{\mathrm{AQ}}[/latex] is parallel to [latex]\overline{\mathrm{PC}}[/latex].
d) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{AD}}[/latex] are perpendicular lines. We denote this by writing [latex]\overline{\mathrm{AB}} \perp \overline{\mathrm{AD}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[/latex] is perpendicular to [latex]\overline{\mathrm{AD}}[/latex].
e) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{BC}}[/latex] are perpendicular lines. We denote this by writing [latex]\overline{\mathrm{AB}} \perp \overline{\mathrm{BC}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[latex] is perpendicular to [latex]\overline{\mathrm{BC}}[/latex] .
f) [latex]\overline{\mathrm{BC}}, \overline{\mathrm{CD}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{BC}} \perp \overline{\mathrm{CD}}[/latex] and can be read as [latex]\overline{\mathrm{BC}}[/latex] is perpendicular to [latex]\overline{\mathrm{CD}}[/latex].
g) [latex]\overline{\mathrm{CD}}, \overline{\mathrm{AD}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{CD}} \perp \overline{\mathrm{AD}}[/latex] and can be read as [latex]\overline{\mathrm{CD}}[/latex] is perpendicular to [latex]\overline{\mathrm{AD}}[/latex].

ii) [latex]\overline{\mathrm{PX}}, \overline{\mathrm{QR}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{PX}} \perp \overline{\mathrm{QR}}[/latex] and can be read as [latex]\overline{\mathrm{PX}}[/latex] is perpendicular to [latex]\overline{\mathrm{QR}}[/latex].

iii) a) [latex]\overline{\mathrm{LM}}, \overline{\mathrm{KN}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{LM}} / / \overline{\mathrm{KN}}[/latex] and can be read as [latex]\overline{\mathrm{LM}}[/latex] is parallel to [latex]\overline{\mathrm{KN}}[/latex].
b) [latex]\overline{\mathrm{MN}}, \overline{\mathrm{LK}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{MN}} / / \overline{\mathrm{LK}}[/latex] and can be read as [latex]\overline{\mathrm{MN}}[/latex] is parallel to [latex]\overline{\mathrm{LK}}[/latex].
c) [latex]\overline{\mathrm{ON}}, \overline{\mathrm{LP}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{ON}} / / \overline{\mathrm{LP}}[/latex] and can be read
as [latex]\overline{\mathrm{ON}}[/latex] is parallel to [latex]\overline{\mathrm{LP}}[/latex]
d) [latex]\overline{\mathrm{LM}}, \overline{\mathrm{ON}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{ON}} \perp \overline{\mathrm{LM}}[/latex] and can be read as [latex]\overline{\mathrm{ON}}[/latex] is perpendicular to [latex]\overline{\mathrm{LM}}[/latex].
e) [latex]\overline{\mathrm{LP}}, \overline{\mathrm{KN}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{LP}} \perp \overline{\mathrm{KN}}[/latex] and can be read as [latex]\overline{\mathrm{LP}}[/latex] is perpendicular to [latex]\overline{\mathrm{KN}}[/latex].

Question 3.
From the given figure find out the Intersecting lines and concurrent lines.

Solution:
i) Intersecting lines : (l, m); (l, n); (n, o); (m, o); (l, o); (m, n)
ii) Intersecting lines: (p, q); (p, r); (p, s); (q, r); (q, s)
Concurrent lines : (p, q, s)

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.2

Question 1.
Measure the lengths of the given line segments.

Solution:
i) [latex]\overline{\mathrm{AB}}[/latex] = 2.4 cm
ii) [latex]\overline{\mathrm{PQ}}[/latex] = 1.5 cm
iii) [latex]\overline{\mathrm{KL}}[/latex] = 1cm, [latex]\overline{\mathrm{LM}}[/latex] = 1 cm
[latex]\overline{\mathrm{KM}}=\overline{\mathrm{KL}}+\overline{\mathrm{LM}}[/latex] =1 + 1 = 2 cm

Question 2.
Draw the following line segments.
i) AB = 6.3 centimeters ii) MN = 3.6 centimeters

Question 3.
Draw PQ = 4.6 cm and extend upto R such that PR = 6 cm.
Solution:

[latex]\overline{\mathrm{PR}}=\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}[/latex] = 4.6 + 1.4 = 6 cm

Question 4.
Draw a line segment [latex]\overline{\mathrm{OP}}[/latex] with certain length and mark a point Q on it.
Check whether [latex]\overline{\mathrm{OP}}-\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}[/latex]
Solution:

Given, [latex]\overline{\mathrm{OP}}[/latex] = 8 cm; [latex]\overline{\mathrm{PQ}}[/latex] = 3 cm
[latex]\overline{\mathrm{OP}}-\overline{\mathrm{PQ}}[/latex] = 8cm – 3cm = 5 cm = [latex]\overline{\mathrm{OQ}}[/latex]
∴ [latex]\overline{\mathrm{OP}}-\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}[/latex] = 5cm

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.1

Question 1.
In the given figure there are some points marked. Name them.

Solution:

Question 2.
Join the points given below. Name the line segments so formed in the figure.

Solution:

[latex]\overline{\mathrm{AD}}[/latex] read as segment AD
[latex]\overline{\mathrm{BC}}[/latex] read as segment BC

[latex]\overline{\mathrm{AB}}[/latex] read as segment AB

[latex]\overline{\mathrm{DC}}[/latex] read as segment DC

[latex]\overline{\mathrm{AB}}[/latex] read as segment AB
[latex]\overline{\mathrm{BC}}[/latex] read as segment BC
[latex]\overline{\mathrm{CD}}[/latex] read as segment CD
[latex]\overline{\mathrm{DE}}[/latex] read as segment DE
[latex]\overline{\mathrm{EF}}[/latex] read as segment EF
[latex]\overline{\mathrm{FA}}[/latex] read as segment FA

Question 3.
Identify the following from the given figure.
(i) Any six points.
(ii) Any six line segments. (Starts with G)
(iii) Any six rays. (With initial point I)
(iv) Any three lines.

Solution:
Points are : A, B, C, D, E, F
G, H, I, and J
ii) Line segments are : [latex]\overline{\mathrm{GF}}, \overline{\mathrm{GE}}, \overline{\mathrm{GD}}, \overline{\mathrm{GH}}, \overline{\mathrm{GC}} \text { and } \overline{\mathrm{GA}}[/latex]
iii) Rays are: [latex]\overrightarrow{\mathrm{IA}}, \overrightarrow{\mathrm{IC}}, \overrightarrow{\mathrm{IB}}, \overrightarrow{\mathrm{ID}}, \overrightarrow{\mathrm{JA}}, \overrightarrow{\mathrm{JC}}, \overrightarrow{\mathrm{JE}}[/latex]
iv)Lines are :

Question 4.
Write ‘True’ or ‘False’.
(i) A line has two end points.
(ii) Ray is a part of line.
(iii) A line segment has two end points.
(iv) We can draw many lines through two points.
Solution:
i) A line has two end points. (False)
ii) Ray is a part of line.(True)
iii) A line segment has two end points.(True)
iv) We can draw many lines through two points.(False)

Question 5.
Draw and Name :
(T) Line containing point K.
QS) Draw a circle and a line such that the line intersects the circle.
a) at no points b) at one point c) at two points
(iii) Can we draw a line and a circle with 3 intersecting points ?
Solution:

iii) No, we can’t draw a line and a circle with 3 intersecting points. As a line can intersect the circle at two points only.

Question 6.
List out all capital letters in English alphabet, that you can write with 3 line segments by using all.
Solution:

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 12 Data Handling InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson Data Handling InText Questions

Let’s Do (Page No. 159)

Question 1.
Take a die. Throw it and record the number. Repeat the activity 40 times and record the numbers. Represent the data in a frequency distribution table using tally marks.
Solution:

(Page No. 159)

Question 1.
In what way is the bar graph better than the pictograph ?
Solution:
Bar graphs are better indicative as they show exact numerical value. Also, to indicate negative values and positive values, it looks easier in a bar graph.