Students can go through AP Board 6th Class Maths Notes Chapter 2 Whole Numbers to understand and remember the concepts easily.
AP State Board Syllabus 6th Class Maths Notes Chapter 2 Whole Numbers
→ Natural numbers: The numbers which we use for counting are called Natural numbers N= {1, 2, 3, 4, 5, 6,…} .
→ Successor: Every natural number has a successor, which is one more than it. Example : Successor of 15 is 15 + 1 = 16
→ Predecessor: Every natural number has a predecessor except 0. Predecessor of a number is one less than it.
Example: Predecessor of 56 is 56 – 1 = 55
![]()
→ Whole numbers: The natural numbers along with zero forms the set of Whole numbers.
W = {0, 1, 2, 3, 4, 5, 6,…}
- Every whole number has a successor and every whole number has a predecessor except zero.
- Every natural number is a whole number and every whole number is a natural number except zero.
- The smallest natural number is 1.
- The smallest whole number is 0.
- Addition, subtraction and multiplication can be represented on a number line.
→ Closure property: Sum of any two whole numbers is always a whole number.
Example : 5 + 3 = 8, a whole number.
This is called closure property of whole numbers w.r.t. addition.
→ Closure property: Product of any two whole numbers is always a whole number. Example : 5 × 3 = 15, a whole number.
This is called closure property of whole numbers w.r.t. multiplication.
In other words whole numbers are closed under addition and multiplication.
But whole numbers are not closed under subtraction and division.
Example: 7 – 12, is not a whole number.
9 ÷ 14, is not a whole number.
Division by zero is not defined.
Example: 5 ÷ 0, is not defined
→ Commutative property: Sum of any two whole numbers taken in any order is always same.
Example: 5 + 3 = 3 + 5 = 8
This is called commutative property of whole numbers w.r.t. addition.
→ Commutative property: Product of any two whole numbers taken in any order is always same.
Example: 5 × 3 = 3 × 5 = 15
This is called commutative property of whole numbers w.r.t. addition.
In other words whole numbers are commutative w.r.t. addition and multiplication. But whole numbers are not commutative w.r.t. subtraction and division.
Example: 4 – 9 ≠ 9 – 4 and 8 ÷ 11 ≠ 11 ÷ 8
![]()
→ Associative property: The sum of any three whole numbers taken in any or der is always same.
Example : 5 + (8 + 3) = (5 + 8) + 3 =16
This is called associative property of whole numbers w.r.t. addition.
→ Associative property: The product of any three whole numbers taken in any order is always same.
Example : 5 × (8 × 3) = (5 × 8) × 3 = 120
This is called associative property of whole numbers w.r.t. multiplication.
In other words whole numbers are associative w.r.t. addition and multiplication.
But whole numbers are not associative w.r.t. subtraction and division.
Example : 5 – (8 – 3) ≠ (5 – 8) – 3
: 5 ÷ (8 ÷ 3) ≠ (5 ÷ 8) ÷ 3
→ Distributive property of multiplication over addition:
(Example: 5 × (8 + 3) = (5 × 8) + (5 × 3) = 55
→ Additive identity: If zero is added to any whole number, then the result is the number itself.- Here zero is called the additive identity.
Example: 5 + 0 = 5, 7 + 0 = 7, 0 + 9 = 9 and so on.
![]()
→ Multiplicative identity: If any whole number is multiplied by 1, then the result is the number itself. Here one is called the multiplicative identity.
Example: 5 × 1 = 5, 7 × 1 = 7, 1 × 9 = 9 and so on.
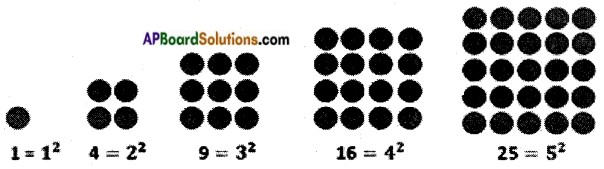
If we represent the number 1 as a (.) dot, then a whole number can be represented either as an array of a triangle or a square.
The triangular numbers are 3, 6, 10, 15, 21, 28, ……. etc.

The square numbers are 4, 9, 16, 25, 36, …… etc.
![]()
→ Multiplication by 9/99/999/9999….etc.
74 × 99 = (74 – 1)/(9 – 7)(10 – 4) = 73/26
256 × 999 = (256 – 1)/(9 – 2)(9 – 5)(10 – 6) = 255/744
4267 × 9999 = (4267 – 1)/(9 – 4)(9 – 2)(9 – 6)(10 – 7) = 4266/5733
Here the number of 9’s in the multiplier is equal to number of digits in the multiplicand.
Answer has two parts: LHS/RHS
LHS: (Multiplicand-1)
RHS: Subtract all digits from 9 but the last digit from 10