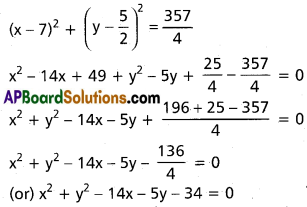Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B System of Circles Solutions Exercise 2(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B System of Circles Solutions Exercise 2(b)
I.
Question 1.
Find the equation of the radical axis of the following circles,
i) x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0
Solution:
S ≡ x² + y² – 3x – 4y + 5 = 0
S ≡ 3x² + 3y² – 7x + 8y + 11 = 0
S – S’ = 0 is radical axis.
(x² + y² – 3x – 4y + 5)
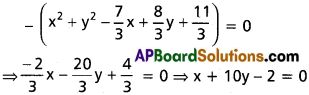
ii) x² + y² + 2x + 4y + 1 = 0, x² + y² + 4x + y = 0.
Solution:
S – S’ = 0 is radical axis.
(x² + y² + 2x + 4y + 1) – (x² +y² + 4x + y) = 0
⇒ -2x + 3y + 1 = 0
(or) 2x – 3y – 1 =0 required radical axis.
iii) x² + y² +4x + 6y – 7 = 0,
4(x² + y²) + 8x + 12y – 9 = 0.
Solution:
S – S’ = 0 is radical axis.
(x² + y² + 4x + 6y – 7) – (x² + y² + 2x + 3y – \(\frac{9}{4}\)) = o
⇒ 2x + 3y – \(\frac{19}{4}\) = 0 ⇒ 8x + 12y – 19 = 0
iv) x² + y² – 2x – 4y -1=0, x² + y² – 4x – 6y + 5 = 0.
Solution:
S – S’ = 0 radical axis
(x² + y² – 2x – 4y – 1) – (x² + y² – 4x – 6y + 5) = 0
2x + 2y – 6 = 0 (or) x + y – 3 = 0
![]()
Question 2.
Find the equation of the common chord of the following pair of circles.
i) x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0.
Solution:
(x² + y² – 4x – 4y + 3) – (x² + y² – 5x – 6y + 4) = 0
x + 2y – 1 = 0 Equation of common chord.
ii) x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
(x² + y² +2x + 3y + 1) – (x² + y² + 4x + 3y + 2) = 0
-2x – 1 = 0 equation of common chord is
iii) (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b)
Solution:
(x² + y² – 2xa – 2yb – c²) – (x² + y² – 2xb – 2ya – c²) = 0
-2x(a – b) – 2y(b – a) = 0
(or) x – y = 0
II.
Question 1.
Find the equation of the common tangent of the following.circles at their point of contact.
i) x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0.
Solution:
x² + y² + 10x – 2y + 22 = 0
x² + y² + 2x – 8y + 8 = 0
When circles touch each other then
S – S’ = 0 is required tangent (common)
∴ (x² + y² + 10x-2y + 22) – (x² + y² + 2x – 8y + 8) = 0
8x + 6y + 14 = 0 (or)
4x + 3y + 7 = 0
ii) x² + y² – 8y – 4 = 0; x² + y² – 2x – 4y = 0.
Solution:
When circles touch each other then
S – S’ = 0 is required common tangent.
(x² + y² – 8y – 4) – (x² + y² – 2x – 4y) = 0
2x – 4y – 4 = 0 (or) x – 2y – 2 = 0
Question 2.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x +, 6y + 6 = 0 touch each other and find the point of contact.
Solution:
C1 = (4, 1) C2 = (1, -3)
r1 = \(\sqrt{16+1-8}\) = 3 ; r2 = \(\sqrt{1+9-6}\) = 2
C1C2 = \(\sqrt{(4-1)^{2}+(1+3^{2})}\) = 5
r1 + r2 = C1 + C2 they touch each other externally
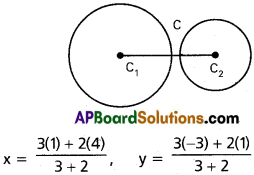
∴ Point of contact is (\(\frac{11}{5} , \frac{-7}{5}\))
Question 3.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other then show that f’g = fg’.
Solution:

![]()
Question 4.
Find the radical centre of the following circles.
i) x² + y² – 4x – 6y + 5 = 0 ………… (i)
x² + y² – 2x – 4y – 1 = 0 ………… (ii)
x² + y² – 6x – 2y = 0 ………… (iii)
Solution:
(i) – (ii) gives
– 2x – 2y + 6 = 0
x + y – 3 = 0 ………. (1)
(ii) – (iii) gives

Point of intersection of (1) and (2) is radical centre will (7/6,11/6) we get by solving these two equations.
ii) x² + y² + 4x – 7 = 0,
2x² + 2y² + 3x + 5y – 9 = 0,
x² + y² + y = 0.
Solution:
S = x² + y² + 4x – 7 = 0 ……….. (i)
S1 = 2x² + 2y² + 3x + 5y – 9 = 0
= x² + y² + \(\frac{3}{2}\)x + \(\frac{5}{2}\)y – \(\frac{9}{2}\) = 0 ………. (ii)
S11 = x² + y² + y = 0 ………. (iii)
Radical axis of S = 0, S1 = 0 is S – S1 = 0
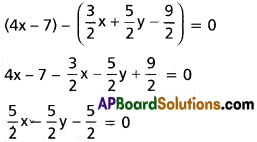
5x – 5y – 5 = 0
x – y – 1 = 0 ………… (iv)
Radical axis of S = 0, S11 = 0 is S – S11 = 0
4x – y – 7 = 0 ……… (v)
x – y – 1 = 0………….. (vi)
Subtracting 3x – 6 = 0 ⇒ 3x = 6
x = \(\frac{6}{3}\) = 2
Substituting in (iv), 2 – y – 1 = 0
y = 1
Radical centre is P(2, 1)
III.
Question 1.
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0 and x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle and also find its length.
Solution:
Common chord be
(x² + y² – 6x – 4y + 9) – (x² + y² – 8x – 6y + 23) = 0
2x + 2y – 14 = 0
x + y – 7 = 0 ………… (i)
Centre of circle (-4, -3)
(-4, -3) lies on line x + y – 7
Radius is {4² + 3² – 23}½ = √2
Diameter = 2√2
Question 2.
Find the equation and length of the common chord of the following circles.
i) x² + y² + 2x + 2y + 1 =0,
x² + y² + 4x + 3y + 2 = 0.
Solution:
x² + y² + 2x + 2y + 1 = 0
x² + y² + 4x + 3y + 2 = 0
Equation of common chord is
S – S’ = 0 (x² + y² + 2x + 2y + 1) – (x² + y² + 4x + 3y + 2) = 0
-2x – y – 1 = 0
2x + y + 1 = 0
Centre of circle is (-1, -1)
Radius = \(\sqrt{1+1-1}\) = 1
Length of ⊥ from centre (-1, -1) to the chord is
d = \(|\frac{2(-1)+(-1)+1}{\sqrt{2^{2}+1^{2}}}|=\frac{2}{\sqrt{5}}\)
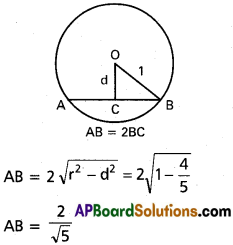
ii) x² + y² – 5x – 6y + 4 = 0, x² + y² – 2x – 2 = 0
Solution:
Common chord equation
(x² + y² – 5x- 6y + 4) – (x²+ y² – 2x – 2) = 0
-3x – 6y + 6 = 0
x + 2y – 2 = 0
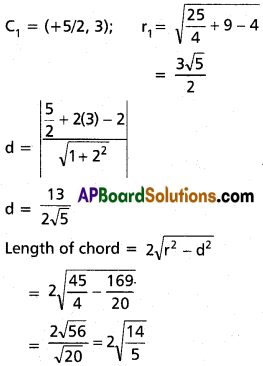
Question 3.
Prove that the radical axis of the circles x² + y² + 2gx + 2fy + c = 0 and x² +y² + 2g’x + 2f’y + c‘ = 0 is the diameter of the latter circle (or the former bisects the circumference of the latter) if 2g'(g – g’) + 2f (f – f’) – c – c’.
Solution:
Radical axis is
(x² + y² + 2gx + 2fy + c) – (x² + y² + 2g’x + 2fy + c’) = 0
2(g – g’) x + 2(f – f’)y + c – c’ = 0 …………. (i)
Centre of second circle is (-g1, -f1)
Radius = \(\sqrt{g’^{2}+f’^{2}+c’}\)
Now (-g’, -f’) should lie on (i)
– 2g (g – g’) – 2f'(f – f’) + c – c’ = 0
(or) 2g (g – g’) + 2f'(f – f’) = c – c’
Question 4.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if 1/a² + 1/b² = 1/c.
Solution:
The centres of the circles C1 (-0, 0) and C2 (0, -b) respectively
Radius of 1st circle be \(\sqrt{a^{2}-c}\) = r1
Radius of 2nd circle be \(\sqrt{b^{2}-c}\) = r2
C1C2 = r1 + r2
(C1 C2)² = (r1 + r2)²
(a² + b²) = a² – c + b² – c + 2\(\sqrt{a^{2}-c}.\sqrt{a^{2}-c}\)
c = \(\sqrt{a^{2}-c}.\sqrt{a^{2}-c}\)
c² = (a² – c) (b² – c)
c² = -c (a² + b²) + a²b² + c²
(or) c(a² + b²) = a²b² (or) \(\frac{1}{c}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\)
![]()
Question 5.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x – 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or internal?
Solution:
For the circle S = x² + y² – 2x = 0
Centre C1 = (1, 0) and Radius r1 .= \(\sqrt{1+0}\) = 1
For the circle S’ = x² + y² + 6x – 6y + 2 = 0
Centre C2 = (-3, 3) and
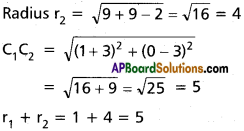
As C1C2 = r1 + r2 the two circles touch each other externally, the point of contact P divides line of centres internally in the ratio
r1 : r2 = 1 : 4
Hence point of contact
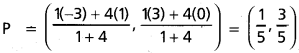
The contact of the circle is external.
Question 6.
Find the equation of the circle which cuts the following circles orthogonally.
i) x² + y² + 4x – 7 = 0,
2x² + 2y² + 3x + 5y – 9 = 0,
x² + y² + y = 0.
Solution:
S = x² + y² + 4x – 7 = 0 ………… (i)
S1 = 2x² + 2y² + 3x + 5y – 9 = 0

x – y – 1 = 0 ……. (iv)
Radical axis of S = 0, S11 = 0 is S – S11 = 0
4x – y – 7 = 0 ……….. (v)
Solving (iv) and (v)
We get 3x – 6 = 0
x = -2
Substute x value in (iv), 2 – y – 1 =0
y = 1
Radical centre is P(2, 1)
PT =’ Length of the tangent from P to S = 0
= \(\sqrt{4+1+8-7}\)
= √6
Equation of the circles cutting the given circles orthogonally
(x – 2)² + (y – 1)² = (√6)²
x² + 4 – 4x + y² + 1 – 2y = 6
x² + y² – 4x – 2y – 1 = 0
ii) x² + y² + 2x + 4y + 1 = 0,
2x² + 2y² + 6x + 8y – 3 = 0,
x² + y² – 2x + 6y – 3 = 0.
Solution:
Equations of the required circles are
S ≡ x² + y² + 2x + 4y + 1 = 0
S1 ≡ x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
S11 ≡ x² + y² – 2x + 6y – 3 = 0
Radical axis of S = 0, S1 = 0 is S – S1 =0
-x + \(\frac{5}{2}\) = 0 ⇒ x = \(\frac{5}{2}\)
Radical axis of S = 0, S11 = 0 is S – S11 = 0
4x – 2y + 4 = 0
⇒ 2x – y + 2 = 0
x = \(\frac{5}{2}\) ⇒ 5 – y + 2 = 0
⇒ y = 7
Radical centre is P (\(\frac{5}{2}\) , 7)
PT = Length of the tangent from P to S = 0

Equation of the circles cutting the given circles orthogonally
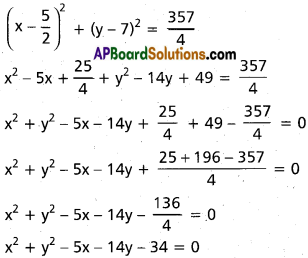
iii) x² + y² + 2x + 17y + 4 = 0,
x² + y² + 7x + 6y + 11 = 0,
x² + y² – x + 22y + 3 = 0
Solution:
Equations of the required circles are
S ≡ x² + y² + 2x + 17y + 4 = 0 ……… (i)
S1 ≡ x² + y² + 7x + 6y + 11 = 0 ……… (ii)
S11 ≡ x² + y² – x + 22y + 3 = 0 ……… (iii)
Radical axis of S = 0, S1 = 0 is S – S1 = 0
-5x + 11 y – 7 = 0
5x – 11y + 7 = 0 ……… (iv)
Radical axis of S = 0, S11 = 0 is S – S11 =0
3x – 5y + 1 = 0 ………… (v)
Solving (iv) and (v)
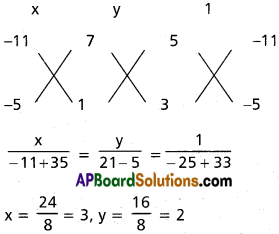
Radical centre is P(3, 2)
PT = Length of the tangeqt from P to S = 0
= \(\sqrt{9+4+6+34+4}\) = √57
Equation of the circle cutting the given circles cutting orthogonally
(x – 3)² + (y – 2)² = 57
x² – 6x + 9 + y² – 4y + 4 – 57 = 0
x² + y² – 6x – 4y – 44 = 0
![]()
iv) x² + y² + 4x + 2y + 1 = 0,
2(x² + y²) + 8x + 6y – 3 = 0,
x² + y² + 6x – 2y – 3 = 0.
Solution:
Equations of the required circles are
S ≡ x² + y² + 4x + 2y + 1 = 0 ……….. (i)
S1 ≡ x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ………… (ii)
S11 ≡ x² + y² + 6x – 2y – 3 = 0 ………. (iii)
(i) – (ii) gives radical axis of S = 0, S1 = 0 is
S – S1 = 0 ⇒ -y + \(\frac{5}{2}\) = 0 ⇒ y = \(\frac{5}{2}\)
Radical axis of S = 0, S11 = 0 is S – S11 = 0
– 2x + 4y + 4 = 0
x – 2y – 2 = 0
y = \(\frac{5}{2}\) ⇒ x – 5 – 2 = 0
x = 5 + 2 = 7
Radical centre is P (7, \(\frac{5}{2}\))
PT = Length of the tangent P to S = 0
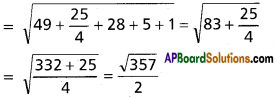
Equation of the required circle is