Inter 2nd Year Maths 2B System of Circles Solutions Ex 2(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B System of Circles Solutions Exercise 2(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B System of Circles Solutions Exercise 2(a)

I.

Question 1.
Find k if the following pairs of circles are orthogonal.
i) x² + y² + 2by – k = 0, x² + y² + 2ax + 8=0.
Solution:
g₁ = 0; f₁ = b; c₁ = -k
g₂ = a; f₂ = 0; c₂ = 8
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(0)(a) +2(b)(0)= -k + 8
0 = – k + 8
k = 8

ii) x² + y² – 6x – 8y + 12 = 0;
x² + y² – 4x + 6y + k = 0
Solution:
g₁ = -3; f₁ = -4; c₁ = 12
g₂ = -2; f₂ = 3; c₂ = k
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(-3)(-2) + 2(3)(-4) = 12 + k
+ 12 – 24 = 12+ k ⇒ k = -24

iii) x² + y² – 5x – 14y – 34 = 0,
x² + y² + 2x + 4y + k = 0
Solution:
g₁ = \(\frac{-5}{2}\) ; f₁ = -7 ; c₁ = -34
g₂ = 1; f₂ = 2; c₂ = k
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(\(\frac{-5}{2}\)(1) + 2(-7)(2) = -34 + k
-5 – 28 = -34 + k
– 33 = – 34 + k
k = 34 – 33
⇒ k = 1

iv) x² + y² + 4x + 8 = 0, x² + y² – 16y +k = 0
Solution:
g₁ =2 ; f₁ = 0 ; c₁ = 8
g₂ = 0 ; f₂ = – 4; c₂ = k
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(2)(0) + 2(0)(-8) = 8 + k
0 + 0 = 8 + k
⇒ k = -8

Question 2.
Find the angle between the circles given by the equations.
i) x² + y² – 12x – 6y + 41 = 0,
x² + y² + 4x + 6y – 59= 0.
Solution:

ii) x² + y²+ 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0.
Solution:

Question 3.
Show that the angle between the circles x + y = a , x + y = ax + ay is \(\frac{3 \pi}{4}\).
Solution:
Equations of the circles are
S ≡ x² + y² – a² = 0
S’ ≡ x² + y² – ax – ay = 0

Question 4.
Show that the circles given by the following equations intersect each other orthogonally.
i) x² + y² – 2x – 2y – 7 = 0,
3x² + 3y² – 8x + 29y = 0.
Solution:
C₁ = (1, 1)
g = -1, f = -1, c =-7
g’ = \(\frac{-4}{3}\), f’ = \(\frac{29}{6}\) ; c’ = o
Condition that two circles are orthogonal is

∴ -7 = -7
Hence both circles cut orthogonally.

ii) x² + y² + 4x – 2y – 11 = 0,
x² + y² – 4x – 8y + 11 =0.
Solution:
g₁ = 2, f₁ = -1, c₁ = -11
g₂ = -2, f₂ = -4, c₂ = 11
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(2)(-2) + 2(-1)(-4) = -11 + 11
-8 + 8 = 0
∴ Two circles are orthogonal.

iii) x² + y² – 2x + 4y + 4 = 0, .
x² + y² + 3x + 4y + 1 = 0.
Solution:
g = -1, f = 2, c = 4
g’ = \(\frac{3}{2}\), f’= 2, c’= 1
2gg’ + 2ff’ = c + c’
2(-1). \(\frac{3}{2}\) + 2 × 2 × 2 = 4 + 1
-3 + 8 = 5
5 = 5
Hence circles cut orthogonally.

iv) x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0.
Solution:
g₁ = -l ; f₁ = 0, c₁ = g, g₂ = 0, f₂ = m, c₂= -g
2g₁g₂ + 2f₁f₂ = c₁ + c₂ is condition for two circles be orthogonal
2(-1)(0) + 2(0)(m) = g – g
0 = 0
∴ Two circles are orthogonal.

II.

Question 1.
Find the equation of the circle which passes through the origin and intersects the circles below, orthogonally.
i) x² + y² – 4x + 6y + 10 = 0, x² + y² + 12y + 6 = 0.
Solution:
Let equation of circle be
x² + y² + 2gx + 2fy + c = 0 ……… (i)
Above circle passes through origin
∴ c = 0
Circle (i) is orthogonal to
x² + y² – 4x + 6y + 10 = 0 then
2g(-2) + 2f(3) = 0 + 10
-4g + 6f = 10 ………… (ii)
Circle (i) is orthogonal to
x² + y² + 12y + 6 = 0
2g(0) + 2f(6) = 6 + 0
12f = 6
f = \(\frac{1}{2}\) …………… (iii)
Solving (ii) and (iii) we get
– 4g + 6 × \(\frac{1}{2}\) = 10
-4g = 10 – 3
g = –\(\frac{7}{4}\)
∴ Equation of circle be
x² + y² – \(\frac{7}{2}\)x + y = 0
2x² + 2y² – 7x + 2y = 0.

ii) x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0.
Solution:
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0
It cuts
x² + y² – 4x – 6y – 3 = 0; x² + y² – 8y + 12 = 0
g₁ = -2, f₁ = -3, c₁ = -3
g₂ = 0 ; f₂ = -4, c₂ = 12
Let g,f, c be constants of required circle.
Required circle passes through origin
∴ c = 0
Requited circle is orthogonal to both circles.
∴ 2g(-2) +2f(-3) = -3 + 0 …………… (i)
2g(0) + 2f(-4) = 12 + 0 …………….. (ii)
Solving (i) and (ii) we get
2g₁g₂ + 2f₁f₂ = c₁ + c₂
Condition of orthogonality
f = –\(\frac{3}{2}\), g = \(\frac{6}{2}\)
Required circle be x² + y² + 6x – 3y = 0

Question 2.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally.
Solution:
Let circle be x² + y² + 2gx + 2fy + c = 0 ……… (i)
(i) is orthogonal with x² + y² – 6x + 3y + 5 = 0
then 2g(-3) + 2f\(\frac{+3}{2}\) = c + 5
-6g + 3f = c + 5 ……… (ii)
(i) is orthogonal with x² + y² – x – 7y = 0
-g – 7f = c ……… (iii)
Circle passes through (0, -3)
0 + 9 – 6f + c = 0 ……… (iv)
(iii) – (ii)
5g – 10f = -5
g – 2f = -1
(iii) + (iv)

x² + y² + \(\frac{4}{3}\)y + \(\frac{2}{3}\)x – 5 = 0
3x² + 3y² + 4y + 2x – 15 = 0
(or) 3x² + 3y² + 2x + 4y – 15 = 0

Question 3.
Find the equation of the circle passing through the origin, having its centre on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let circle be x² + y²+ 2gx + 2fy + c = 0
Equation is passing through (0, 0)
0 + 0 + 2g.0 + 2f.0 + c = 0 ⇒ c = 0
x² + y² + 2gx + 2fy = 0
Centre passes through x + y = 4
∴ -g – f = 4 ………. (i)
Circle is orthogonal to
x² + y² – 4x + 2y + 4 = 0
-4g + 2f = 4 + 0
f – 2g = 2 ……… (ii)
Solving (i) and (ii) we get
– 3g = 6
9 = -2
f = -2
Equation of circle be x² + y² – 4x – 4y = 0

Question 4.
Find the equation of the circle which passes through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0.
Solution:
Let equation of circle be
x² + y² + 2gx + 2fy + c = 0
Passes through (2, 0), (0, 2) then

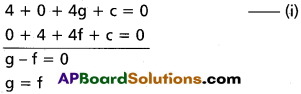
Orthogonal to x + y + \(\frac{5}{2}\)x – \(\frac{6}{2}\)y + 2 = 0
2g\(\frac{5}{4}\) + 2f(-\(\frac{2}{2}\)) = 2 + c
\(\frac{5}{2}\)g – 3f = 2 + c
But g = f
\(\frac{5}{2}\)g – 3g = 2 + c
⇒ -g = 4 + 2C
Putting value of g in equation (i)
-16 – 8c + c = -4
c = –\(\frac{12}{7}\)
– g = 4 – \(\frac{24}{7}\) = +\(\frac{4}{7}\)
g = \(\frac{-4}{7}\) = f
Equation of the circle is
x + y – \(\frac{8x}{7}\) – \(\frac{8y}{7}\) – \(\frac{12}{7}\) = 0
⇒ 7(x² + y²) – 8x – 8y – 12 = 0

Question 5.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y- 7 = 0 and having a centre at (2, 3).
Solution:
The given circle is
x² + y² – 4x + 2y – 7 = 0 ……. (1)
Let the required circle which, cuts orthogonally the circle (1) is
x² + y² + 2gx + 2fy + c = 0 ………… (2)
Its centre is (-g, -f) = (2, 3) given
g = -2, f = -3
The two circles (1) and (2) are cutting each other orthogonally.
So 2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(-2)(-2) + 2(-3)(1) = – 7 + c
8 – 6 = -7 + c
+ 2 = -7 + c
c = 7 + 2 = 9 ⇒ c = 9
Hence the required circle is,
x² + y² – 4x – 6y + 9 = 0

III.

Question 1.
Find the equation of the circle which intersects the circle
x² + y² – 6x + 4y – 3 = 0 orthogonally and passes through the point (3, 0) and touches Y-axis.
Solution:
Let circle be (x – h)² + (y – k)² = r²
If circle touches Y-axis then co-ordinate of centre (h, k); radius = |h|
(x – h)² + (y – k)² = h²
x² – 2hx + h² + y²
-2ky + k² = h²
Orthogonal to
x² + y² – 6x + 4y – 3 = 0
2(-h) (-3) + 2(-k) (2) = -3 + k²
6h – 4k = -3 + k²
x² – 2hx + y²
-2ky + k² = h
Passes through (3, 0) 6h – 4k + 3 – k² = 0
9 – 6h + k² = 0 ……… (ii)
Adding .(i) and (ii) we get
c = 9
12 – 4k = 0 or k = 3, h = 3,
Equation of circle be y² + x² – 6x – 6y + 9 =0.

Question 2.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 =0 and x² + y² – 10x – 4y + 2t = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7.
Solution:
Let circle be x² + y² + 2gx + 2fy + c = 0 ………. (i) Orthogonal to circle
2g(-2) + 2f(-3) = 11 + c ……… (ii)
2g (-5) + 2f(-2) = 21 + c ……….. (iii)
Subtracting it we get
-6g + 2f = 10 ………. (iv)
Circles centre is on 2x + 3y = 7
∴ -2g – 3f = 7 …….. (v)
Solving (iv) and (v)
f = -1, g = -2, c = 3
Equation of circle be x² + y² – 4x – 2y + 3 = 0

Question 3.
If P, Q are conjugate points with respect to a circle S ≡ x² + y² + 2gx + 2fy + c = 0 then prove that the circle PQ as diameter cuts the circles S = 0 orthogonally.
Solution:
Let P = (x₁, y₁) and Q(x₂, y₂) be the conjugate points w.r.t. the circle
S ≡ x² + y² – a² = 0 …….. (i)
Polar of P w.r.t.(1) is xx₁ + yy₁ – a² = 0 ………… (ii)
Given P and Q are conjugate points ⇒ Q lies on (ii)
x₁x₂ + y₁y₂ – a² = 0 …….. (iii)
Equation of the circle on PQ as diameter is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ x² + y² – (x₁ + x₂) x – (y₁ + y₂)y + (x₁x₂ + y₁y₂) = 0 …………… (iv)
(i) and (iv) are orthogonal.
2g₁g₂ + 2f₁f₂ = 2[0(\(\frac{-x_{1}+x_{2}}{2}\)) + 0(\(\frac{-y_{1}+y_{2}}{2}\))]
c₁ + c₂ = -a² + a²
⇒ 2g₁g₂ + 2f₁f₂ = c₁ + c₂
∴ The circle on PQ as diameter cuts S orthogonally.

Question 4.
If the equations of two circles whose radii are a, a’ are S = 0 and S’ = 0, then show that the circles \(\frac{S}{a}+\frac{S’}{a’}\) = 0 and \(\frac{S}{a}-\frac{S’}{a’}\) = 0 intersect orthogonally.
Solution:
Let 2d be the distance between the centres of the circles S = 0 and S’ =. 0. Take the line joining the centres as X-axis and the point midway between the centres as origin.
Then the equations of the circles are
S ≡ (x – d)² + y² – a² = 0
S’ ≡ (x + d)² + y² – a² = 0
∴ \(\frac{S}{a}+\frac{S’}{a’}\) =0 becomes Sa’ + S’a = 0
(or) [(x – d)² + y² -a²]a’ + [(x + d)² + y² – a’²]a = 0
(or) x² + y² + 2{\(\frac{(a-a’)d}{(a+a’)}\)}x + (d² – aa’) = 0 ………… (i)
Putting -a’ for a’ in we get \(\frac{S}{a}-\frac{S’}{a’}\) = 0
reduces to x² + y² + 2{\(\frac{(a+a’)d}{(a-a’)}\)}x + (d² + aa’) = 0 ………… (ii)
If (i) and (ii) cut orthogonally then
L.H.S. = 2gg’ + 2ff = c + c’
= 2{\(\frac{(a+a’)d}{(a-a’)}\)}{\(\frac{(a+a’)d}{(a-a’)}\)} + 2(0). (0) = 2d²
= (d² – aa’) + (d² + aa’) = 2d²
Which being true the circles (i) and (ii) the circles \(\frac{S}{a}±\frac{S’}{a’}\) = 0 cut each other at right angles.

Question 5.
Find the equation of the circle which intersects each of the following circles orthognally
i) x² + y² + 2x + 4y + 1 = 0, x² + y² – 2x + 6y – 3 = 0, 2(x² + y²) +6x + 8y – 3 = 0.
Solution:
Let equation of circle be
x² + y² + 2gx + 2fy + c = 0
Given circle is orthogonal to all 3 circles then
2g(1) + 2f(2) = c + 1 ……….. (i)
2g(\(\frac{3}{2}\)) = 2f(2) = c – \(\frac{3}{2}\) ………… (ii)
2g (-1) +2f(3) = c – 3 ………… (iii)
(iii) – (ii)
-5g + 2f = \(\frac{-3}{2}\) (or) – 10g + 4f = -3 ……….. (iv)
(iii) – (i)
-4g + 2f = – 4
f – 2g = -2 ……….. (v)
Solving (iv) and (v) we get
f = -7, g = -5/2, c = -34
∴ Equation of circle be
x² + y² – 5x – 14y – 34 = 0

ii) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0.
Solution:
Let required circle equation be
x² + y² + 2gx + 2fy + c = 0 this circle is orthogonal to above three circles.
∴ 2g(2) + 2f(1) = c + 1 ……….. (i)
2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\) ……….. (ii)
2g(3) + 2f(-1) = c – 3 ……….. (iii)
(i) – (ii) we get (ii) – (iii) we get
– f = \(\frac{5}{2}\) then – 2g + 5f = \(\frac{3}{2}\)
We get
g = -7 and f = \(\frac{-5}{2}\)
Substituting ‘g’ and ‘f’ in (i) we get
4(-7) + 2(\(\frac{-5}{2}\)) = c + 1
c = -34
Required equation of circle be
x² +y² – 5y – 14x – 34 = 0

Question 6.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at the points A and B, then find the equation of the circle having AB as diameter.
Solution:
Equation of circle passing through x² + y² – 4 and 2x + 3y – 1 =0 can be written as
(x² + y² – 4) + λ(2x + 3y – 1) = 0
x² + y² + 2λx + 3λy – 4 – λ = 0
Centre : (-λ, \(\frac{-3 \lambda}{2}\))
Centre lies on 2x + 3y – 1 =0
∴ 2(-λ) + 3(\(\frac{-3 \lambda}{2}\)) – 1 = 0
λ = \(\frac{-2}{13}\)
∴ Equation of circle be
13 (x² + y²) – 4 x 13 – 2(2x + 3y- 1) = 0
13 (x² + y²) – 4x – 6y – 50 = 0.

Question 7.
If x + y = 3 is the equation of the chord AB of the circle x² + y² – 2x + 4y – 8 = 0, find the equation of the circle having \(\overline{\mathrm{AB}}\) as diameter.
Solution:
Required equation of circle passing through intersection S = 0 and L = 0 is S + λL = 0
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
(x² + y² + x(-2 + λ) + y (4 + λ) – 8 – 3λ = 0 ………… (i)
x² + y² + 2gx + 2fy + c = 0 ………… (ii)
Comparing (i) and (ii) we get

2 – λ – 4 – λ = 6
-2λ = 8 ⇒ λ = -4
Required equation of circle be
(x² + y² – 2x + 4y – 8) – 4(x + y – 3) = 0
x² + y² – 6x + 4 = 0

Question 8.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{y}{b}\) = 2.
Solution:
Equation of circle passes through
x² + y² – 2ax = 0 and x² + y² – 2by = 0 can be written as
x² + y² – 2ax + X (x² + y² – 2by) = 0
x²(1 + λ) + y²(1 + λ) + x(-2a) – (2bλ)y = 0

1- λ = (1 + λ)
λ = -1/3
Equation of circle be
3x² + 3y² – 6ax – x² – y² + 2by = 0
⇒ 2x² + 2y² – 6ax + 2by = 0
⇒ x² + y² – 3ax + by = 0