Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(a)
I. Evaluate the following integrals.
Question 1.
∫(x³ – 2x² + 3) dx on R.
Solution:
∫(x³ – 2x² + 3) dx = \(\frac{x^4}{4}-\frac{2}{3}\)x³ + 3x + c
Question 2.
∫2x√x dx on (0, ∞).
Solution:
∫2x√x dx = 2 ∫ x3/2 dx = \(\frac{2x^{5/2}}{5/2}\)
= \(\frac{4}{5}\)x5/2 + c
Question 3.
∫\(\sqrt[3]{2 x^2}\) dx’on (0, ∞).
Solution:
∫\(\sqrt[3]{2 x^2}\) dx = ∫ 21/3. x2/3 dx
= 21/3. \(\frac{x^{5/3}}{5/3}\) + c
= \(\sqrt[3]{2}\).\(\frac{3}{5}\)x5/3 + c
Question 4.
∫\(\frac{x^2+3x-1}{2x}\)dx, x ∈ I ⊂ R\{0}.
Solution:

![]()
Question 5.
∫\(\frac{1-\sqrt{x}}{x}\)dx on (0, ∞).
Solution:
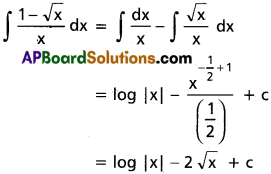
Question 6.
∫(\(1+\frac{2}{x}-\frac{3}{x^2}\)) dx on I⊂R\{0}
Solution:
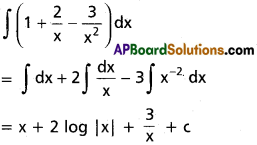
Question 7.
∫(x + \(\frac{4}{1+x^2}\))dx on R.
Solution:
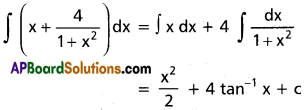
Question 8.
∫(ex \(\frac{1}{x}-\frac{2}{\sqrt{x^2+1}}\))dx on I⊂R\[-1, 1].
Solution:
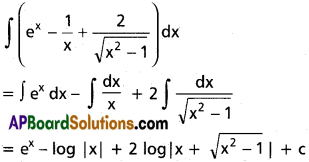
Question 9.
∫(\(\frac{1}{1-x^2}+\frac{1}{1+x^2}\))dx on (-1, 1).
Solution:
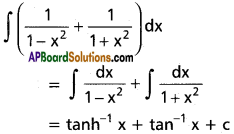
Question 10.
∫(\(\frac{1}{1-x^2}+\frac{2}{1+x^2}\))dx on (-1, 1).
Solution:
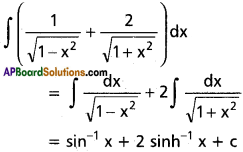
Question 11.
∫elog(1+tan²x) dx on I ⊂ R \{\(\frac{(2n+1)\pi}{2}\):n ∈ Z}
Solution:
∫elog(1+tan²x) dx = ∫elog(sec²x) dx
= ∫sec²x dx = tan x + c
![]()
Question 12.
∫\(\frac{\sin^{2}x}{1+\cos2x}\) dx on I ⊂ R \{(2n ± 1)π : n ∈ Z}
Solution:
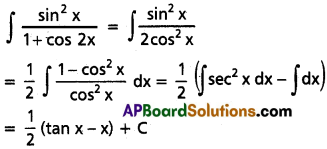
II. Evaluate the following intergrals.
Question 1.
∫(1 – x²)³ dx on (-1, 1).
Solution:
∫(1 – x²)³ dx = ∫(1 – 3x² + 3x4 – x6)dx
= x – x³ + \(\frac{3}{5}\)x5 – \(\frac{x^7}{7}\) + c
Question 2.
∫(\(\frac{3}{\sqrt{x}}-\frac{2}{x}+\frac{1}{3x^2}\)) dx on (0, ∞).
Solution:
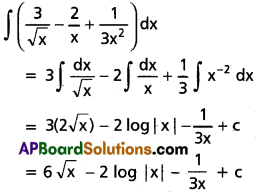
Question 3.
∫(\(\frac{\sqrt{x}+1}{x}\))² dx on (0, ∞).
Solution:

Question 4.
∫(\(\frac{(3x+1)^2}{2x}\)) dx, x ∈ I ⊂ R\ {0}.
Solution:
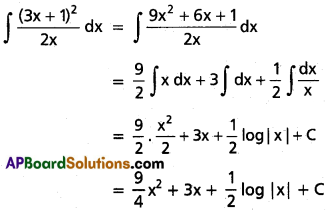
Question 5.
∫(\(\frac{2x-1}{3\sqrt{x}}\))² dx on (0, ∞).
Solution:

![]()
Question 6.
∫(\(\frac{1}{\sqrt{x}}+\frac{2}{\sqrt{x^2-1}}-\frac{3}{2x^2}\))² dx on (0, ∞).
Solution:

Question 7.
∫(sec² x – cos x + x²) dx, x ∈ I ⊂ R/{\(\frac{n \pi}{2}\) : n is an odd integer}.
Solution:
∫(sec² x – cos x + x²) dx
= ∫sec² x dx – ∫cos x + ∫x² dx
= tan x – sin x + \(\frac{x^3}{3}\) + C
Question 8.
∫(sec x tan x + \(\frac{3}{x}\) – 4) dx, x ∈ I ⊂ R\ ({\(\frac{n \pi}{2}\) : n is an odd integer} ∪ {0}).
Solution:
∫(sec x tan x + \(\frac{3}{x}\) – 4) dx
= sec x tan x dx + 3∫\(\frac{dx}{x}\) – 4 ∫dx
= sec x + 3 log |x| – 4x + c
Question 9.
∫(√x – \(\frac{2}{1-x^2}\)) dx on (0, 1).
Solution:

Question 10.
∫(x³ – cos x + \(\frac{4}{\sqrt{x^2+1}}\)) dx
Solution:
∫(x³ – cos x + \(\frac{4}{\sqrt{x^2+1}}\)) dx
= ∫ x³ dx – ∫cos x dx + 4 ∫\(\frac{dx}{\sqrt{x^2+1}}\)
= \(\frac{x^4}{4}\) – sin x + 4 sinh-1 x + C
Question 11.
∫(cosh x + \(\frac{1}{\sqrt{x^2+1}}\))dx, x ∈ R.
Solution:
∫(cosh x + \(\frac{1}{\sqrt{x^2+1}}\))dx
= ∫cosh x dx + ∫\(\frac{dx}{\sqrt{x^2+1}}\)
= sinh x + sinh-1 x + c
Question 12.
∫(sinh x + \(\frac{1}{(x^2-1)^{1/2}}\)) dx, x ∈ I ⊂ (-∞, -1) ∪ (1, ∞).
Solution:
∫(sinh x + \(\frac{1}{(x^2 – 1)^{1/2}}\)) dx
= ∫sinh x dx + ∫\(\frac{dx}{\sqrt{x^2-1}}\)
= cosh x + log(x + \(\sqrt{x^2-1}\)) + C
![]()
Question 13.
∫\(\frac{a^{x}-b^{x}}{a^{x}b^{x}}\) dx (a > 0, a ≠ 1 and b > 0, b ≠ 1) on R.
Solution:

Question 14.
∫sec² x cosec² x dx on I ⊂ R\ (nπ : n ∈ Z} ∪ { (2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}).
Solution:
∫sec² x cosec² x dx
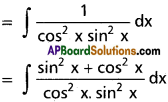
= ∫\(\frac{1}{\cos^{2}x}\)dx + ∫\(\frac{1}{(\sin^{2}x}\)dx
= ∫sec² x dx + ∫cosec² x dx
= tan x – cot x + C
Question 15.
∫\(\frac{1+\cos^{2}x}{1+\cos2x}\) dx on I ⊂ R\{nπ :n ∈ Z}
Solution:
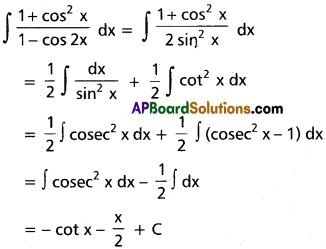
Question 16.
∫\(\sqrt{1-cos2x}\)dx on I ⊂ [2nπ, (2n + 1)π], n ∈ Z.
Solution:
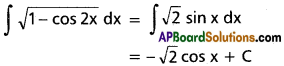
Question 17.
∫\(\frac{1}{\cosh x+\sinh x}\) dx on R.
Solution:
∫\(\frac{1}{\cosh x+\sinh x}\) dx
= ∫\(\frac{\cosh x-\sinh x}{\cosh^{2}x-\sinh^{2}x}\) dx
= ∫(cosh x – sinh x) dx
= sinh x – cosh x + C
![]()
Question 18.
∫\(\frac{1}{1+\cos x}\) dx on I ⊂ R \{(2n + 1)π : n ∈ Z}.
Solution:
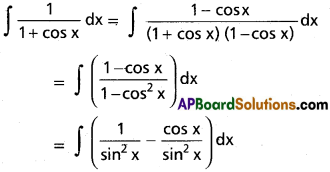
= ∫cosec² (x) dx – ∫cosec x cot x dx
= -cot x + cosec x + C