Inter 2nd Year Maths 2B Circle Solutions Ex 1(e)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Circle Solutions Exercise 1(e) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Circle Solutions Exercise 1(e)

I.

Question 1.
Discuss the relative position of the following pair of circles.
i) x² + y² – 4x – 6y – 12 = 0
x² + y² + 6x + 18y + 26 = 0.
Solution:
Centres of the circles are A (2, 3), B(-3, -9)
radii are r₁ = \(\sqrt{4+9+12}\) = 5
r₂ = \(\sqrt{9+81-26}\) = 8
AB = \(\sqrt{(2+3)^{2}+(3+9)^{2}}\)
= \(\sqrt{25+144}\) = 13 = r₁ + r₂
∴ The circles touch externally.

ii) x² + y² + 6x + 6y + 14 = 0,
x² + y² – 2x – 4y – 4 = 0.
Solution:
Centres are A (-3, -3), B (1, 2)
r₁ = \(\sqrt{9+9-14}\) = 2,
r₂ = \(\sqrt{1+4+4}\) = 3
AB = \(\sqrt{(-3-1)^{2}+(-3-2)^{2}}\)
= \(\sqrt{16+25}=\sqrt{41}\) > r₁ + r₂
∴ Each circle lies exterior to the other circle.

iii) (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)²= 4
Solution:
Centres are A( 2, -1), B(-1, 3)
r₁ = \(\sqrt{4+1+4}\) = 3, r₂ = \(\sqrt{1+9-6}\) = 2
AB = \(\sqrt{(2+1)^{2}+(-1-3)^{2}}\)
= \(\sqrt{9+16}\)
= 5 = r₁ + r₂
∴ The circles touch each other externally.

iv) x² + y² – 2x + 4y – 4 = 0, x² + y² + 4x – 6y – 3 = 0
Solution:
Centres are A (1, -2), B (-2, 3)
r₁ = \(\sqrt{1+4+4}\) = 3, r₂ = \(\sqrt{4+9+3}\) = 4
AB = \(\sqrt{(1+2)^{2}+(-2-3)^{2}}=\sqrt{9+16}\)
= \(\sqrt{9+25}=\sqrt{34}\) < r₁ + r₂
r₁ – r₂ < AB < r₂ + r₁
∴ The circles intersect each other.

Question 2.
Find the number of possible common tangents that exist for the following pairs of circles.
i) x² + y² + 6x + 6y + 14 = 0,
x² + y² – 2x – 4y – 4 = 0
Solution:
c₁ ( -3, -3) c₂ = (1, 2)

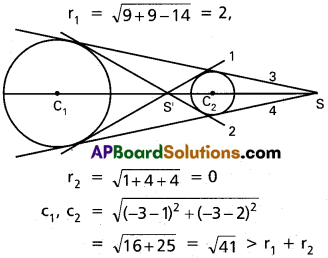
The circles are externally No. of common tangents = 4

ii) x² + y² – 4x – 2y + 1 = 0;
x² + y² – 6x – 4y + 4 = 0.
Solution:
C₁ (2, 1), C₂ = (3, 2)
r₁ = \(\sqrt{4+1-1}\) = 2
r₂ = \(\sqrt{9+4-4}\) =3

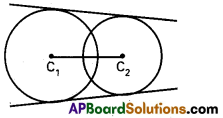
C₁ C₂ = \(\sqrt{(2-3)^{2}+(1-2)^{2}}=\sqrt{2}\)
C₁ C₂ < r₁ + r₂ intersect each other 2 tangents (direct)

iii) x² + y² – 4x + 2y – 4 = 0;
x² + y² + 2x – 6y + 6 = 0.
Solution:
C₁ (2, -1) C₂ = (-1, 3)

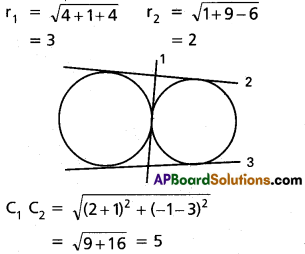
C₁ C₂ = r₁ + r₂ touch each other externally; No. of common tangents = 3.

iv) x² + y² = 4; x² + y² – 6x – 8y + 16 = 0
Solution:

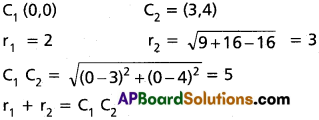
Two circles touch each other.
2 – direct tangents
1 – transverse tangent (at common point)

v) x² + y² + 4x – 6y – 3 = 0
x² + y² + 4x – 2y + 4 = 0.
Solution:
C₁ (-2, 3) C₂ = (-2, 1)
r₁ = \(\sqrt{4+9+3}\) = 4 r₂ = \(\sqrt{4+1-4}\) = 1
C₁ C₂ = \(\sqrt{(-2+2)^{2}+(3-1)^{2}}\)
C₁ C₂ = 2 < 3 = r₁ – r₂
One circle is inside the other.
∴ No common tangent.

Question 3.
Find the internal centre of similitude for the circles x² + y² + 6x – 2y + 1 =0 and x² + y² – 2x – 6y + 9 = 0.
Solution:

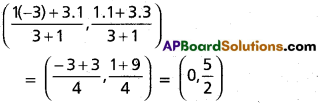
The internal centre of similitude S divides
C₁ C₂ internally in the ratio r₁ : r₂ = 3 : 1
Co-ordinates of S¹ are

Question 4.
Find the external centre of similitude for the circles x² + y² – 2x – 6y + 9 = 0 and x² + y² = 4.
Solution:
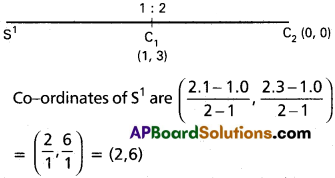
Centre of the circle C₁ (1, 3) and C2 (0,0)
r₁ = \(\sqrt{1+9-9}\), r₂ = 2
External centre of similitude S¹ divides C₁ C₂ externally in the ratio
r₁ : r₂ = 1 : 2

II.

Question 1.
i) Show that the circles x² + y² – 6x – 2y + 1 = 0 ; x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact.
Solution:
Equations of the circles are
S₁ ≡ x² + y² – 6x – 2y + 1 =0
S₂ ≡ x² + y² + 2x – 8y + 13 = 0

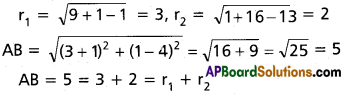
∴ The circles touch each other externally.
The point of contact P divides AB – internally in the ratio r₁ : r₂ = 3 : 2
Co-ordinates of P are
(\(\frac{3(-1)+2.3}{5}\), \(\frac{3.4+2.1}{5}\) i.e., P(\(\frac{3}{5}\), \(\frac{14}{5}\))
Equation of the common tangent is S₁ – S₂ = 0
-8x + 6y – 12 = 0 (or) 4x – 3y + 6 = 0

ii) Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact.
Solution:
Equations of the circles are
S₁ ≡ x² + y² – 6x – 9y + 13 = 0
S₂ ≡ x² + y² – 2x – 16y = 0
centres are A (3, \(\frac{9}{2}\)), B(1, 8)

∴ The circles touch each other internally. The point of contact ‘P’ divides AB externally in the ratio r₁ : r₂ = \(\frac{\sqrt{65}}{2}\) : √65
= 1 : 2 Co-ordinates of P are

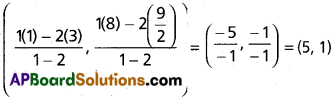
P = (5, 1)
∴ Equation of the common tangent is
S₁ – S₂ = 0
– 4x + 7y +13 = 0
4x – 7y – 13 = 0

Question 2.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius 5.
Solution:
x² + y² – 2x – 4y – 20 = 0 ,
C = (1, 2)

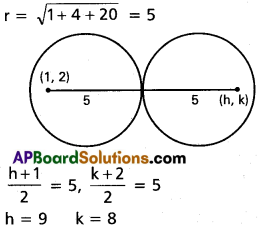
Equation of circle be
(x – 9)² + (y – 8)²
x² + y² – 18x – 16y + 120 = 0
If (h, k) is the centre of the required circle (5, 5) is the mid-point of (1, 2) and (h, k).

Question 3.
Find the direct common tangents of the circles.
x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0.
Solution:
C₁ = (-11, 2) C₂ = (11, -2)
r₁ = \(\sqrt{121+4+100}\) = 15
r₂ = \(\sqrt{121+4-100}\) = 5
Let y = mx + c be tangent
mx – y + c = 0
⊥ from (-11, 2) to tangent = 15
⊥ from (11 ,-2) to tangent = 5


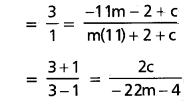
c = -22 m – 4
∴ y = mx – 22m – 4
This line is a tangent to the second circle
∴ \(\frac{|11m+2-22m-4|}{\sqrt{m^{2}+1}}\) = 5
Squaring and cross multiplying
25(1 + m²) = (11m + 2 – 22m – 4)²
96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28m – 21 = 0

⇒ 24y = 7x – 250
⇒ 7x – 24y – 250 = 0

Question 4.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0.
Solution:
C₁ = (2, 5), C₂ = (-2, 3)

= [\(\frac{4}{4}\), \(\frac{9}{2}\)] = [1, \(\frac{9}{2}\)]
Equation of the pair transverse of the common tangents is

Question 5.
Find the pair of tangents from (4, 10) to the circle x² + y² = 25.
Solution:
SS₁₁ = S²₁
(x² + y² – 25) (16 + 100 – 25)
= (4x + 10 y -25)²
91x² + 91y² – 2275
= [16x² + 100y² + 625 + 80xy – 200x – 500y]
75x² – 9y² – 80xy + 500y + 200x – 2900 = 0

Question 6.
Find the pair of tangents drawn from (0,0) to x2 + y2 + 10x + 10y + 40 = 0.
Solution:
S.S₁₁ = S²₁
(x² + y² + 10x + 10y + 40) (40) = [5x + 5y + 40]²
8(x² + y² + 10x + 10y + 40) = (x + y + 8)²5
8x² + 8y² + 80x + 80y + 320
= 5x² + 5y² + 10xy + 80x + 80y + 320
3x² + 3y² – 10xy = 0

III.

Question 1.
Find the equation of the circle which touches x² + y² – 4x + 6y – 12 = 0 at (-1, 1) internally with a radius of 2.
Solution:
C₁ = (2, -3)
r₁ = \(\sqrt{4+9+12}\) = 5

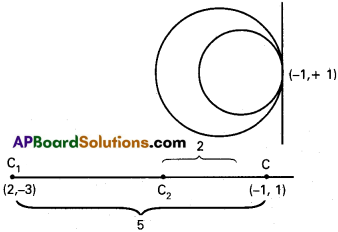
Let C₂ = (h, k)
point of contact – (x, y) = (-1, 1)
since the two circles touch internally

Equation of a circle with centre (\(\frac{1}{5}\), \(\frac{-3}{5}\)) and radius 2 is given by
(x – \(\frac{1}{5}\))² + (y + \(\frac{1}{5}\))² = 4
5x² + 5y² – 2x + 6y – 18 = 0

Question 2.
Find all common tangents of the following pairs of circles.
(i) x² + y² = 9 and x² + y² – 16x + 2y + 49 = 0
Solution:
The circles are x² + y² = 9
x² + y² – 16x + 2y + 49 = 0
Centre are A (0, 0), B(8, -1)

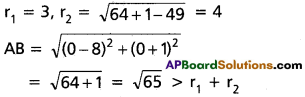
The circles lie outside each other.
A (0, 0), B (8, -1)
External center of similitude S divides AB externally in this ratio 3 : 4
Co-ordinates of are (-24, + 3)
Suppose m is the slope of the direct common tangents
y – 3 = m(x + 24)
= mx + 24m
mx – y 4- (24m + 3) = 0 ………… (1)
This is a tangent to the circle x² + y² = 9
3 = \(\frac{|24m+3|}{\sqrt{m^{2}+1}}\)
9(m² +1 = 9(m² + 1) = 9(8m + 1)²
= 64m² + 16m + 1
63m² + 16m = 0
m(63m + 16) = 0
m = 0 or \(\frac{-16}{63}\).

Case (i): m = 0
Substituting in (1), equation of the tangent is
-y + 3 = 0
y – 3 = 0

Case (ii) : m = \(\frac{-16}{63}\).
Equation of the tangent is

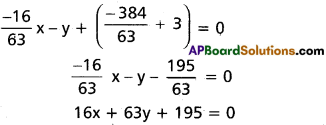
Internal center of similitude S’ divides AB internally in the ratio 3 : 4
Co-ordinates of S’ are (\(\frac{24}{7}\), \(\frac{-3}{7}\))
Equation of the transverse common tangent is

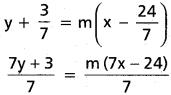
7y + 3 = 7mx – 24m
7mx – 7y – (24m + 3) = 0 ………… (2)
This is a tangent to the circle x² + y² = 9
3 = \(\frac{|24m+3|}{\sqrt{49m^{2}+49}}=\frac{3}{\sqrt{7}} \frac{|28m+1|}{\sqrt{m^{2}+1}}\)
49 (m² + 1) = (8m + 1)²
49m² + 49 = 64m² +16m + 1
15m² + 16m – 48 = 0
(3m – 4) (5m + 12) = 0
m = \(\frac{4}{3}\) or \(\frac{-12}{5}\)

Case (i): Substituting in (2), equation of the tangent is

Case (ii): m = \(\frac{-12}{5}\)
Equation of the transverse common tangent is ie

∴ Equation of direct common tangents are
y – 3 = 0; 16x + 63y + 195 = 0
Equation of transverse common tangents are
4x – 3y – 15 = 0 and 12x + 5y – 39 = 0

ii) x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0
Solution:
r₁ = \(\sqrt{4+1+4}\) = 3, r₂ = \(\sqrt{4+1+4}\) = 1
External center of similitude S divides AB externally in the ratio 3 : 1
3 : 1 A (-2,-1), S’ B (2, 1) S
Co-ordinates of S are
(\(\frac{3.2-(-2)1}{3-1}\), \(\frac{3.1-1(-1)}{3-1}\)) = (4, 2)
Suppose m is the slope of the tangent Equation of the tangent can be taken as
y – 2 = m(x – 4)
= mx – 4m
mx – y + (2 – 4m) = 0 ………… (1)
This is a tangent to the circle
x² + y² + 4x + 2y – 4 = 0

Squaring and cross-multiplication is
(1 – 2m)² = (m² + 1)
4m² – 4m + 1 = m² + 1
3m² – 4m = 0
m(3m-4) = 0
m,= 0 or = \(\frac{4}{3}\)
m = 0
Substituting in (1), equation of the tangent is y + 2 = 0 or y -2 = 0
m = \(\frac{4}{3}\)
Substituting in (1), equation of the tangent is
\(\frac{4}{3}\)x – y + (2 – \(\frac{16}{3}\)) = 0
⇒ \(\frac{4}{3}\)x – y –\(\frac{10}{3}\) = 0
4x – 3y – 10 = 0
Internal centre of similitude S’ divides AB internally in the ratio 3 : 1
Co-ordinates of S’ are
(\(\frac{6-2}{3+1}\), \(\frac{3-1}{3+1}\)x) = (1, \(\frac{1}{2}\))
Equation of the tangent can be taken as
y – \(\frac{1}{2}\) = m(x – 1)
= mx – m
mx – y + (\(\frac{1}{2}\) – m) = 0 ………. (2)
This is a tangent to the circle
x² + y² + 4x + 2y – 4 = 0

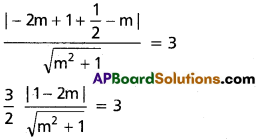
Squaring and cross-multiply is
(1 – 2m)² = 4(m² + 1)
1 + 4m² – 4m = 4m² + 4
Here then value of m is a, so that the tangent is a vertical line, equation of the tangent is
x = \(\frac{1}{2}\)
x – 1 = 0
4m + 3 = 0
m = \(\frac{-3}{4}\)
Substituting in (2), equation of the tangent is
\(\frac{-3}{4}\)x – y + (\(\frac{1}{2}+\frac{3}{4}\)) = 0
-3x – 4y + 5 = 0
3x + 4y – 5 = 0
Equation of direct common tangents are
y – 2 = 0, 4x – 3y – 10 = 0
Equation of transvere common tangents are
x – 1 = 0, 3x + 4y – 5 = 0

Question 3.
Find the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
S.S₁₁ = S²₁
(x² + y² – 6x + 4y – 2)
(9+ 4 – 6 × 3 + 4 × 2 – 2)
= (3x + 2y – 3(x + 3) + 2(y + 2) – 2)²
(x² + y² – 6x + 4y – 2) = (4y – 7)²
x² + y² – 6x + 4y – 2 = 16y² – 56y + 49
x² – 15y² – 6x + 60y – 51 = 0

Question 4.
Find the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 and also find the angle between them.
Solution:
S.S₁₁ = S²₁
(x² + y² – 2x + 4y -11) (1 + 9-2 + 12-11) = [x + 3y – 1 (x + 1) + 2 (y + 3)- 11]²
(x² + y² – 2x + 4y – 11)9 = [5y-6]²
9x² + 9y² – 18x + 36y – 99
25y²+ 36 – 60 y
9x² – 16y² – 18x + 96y – 135 = 0

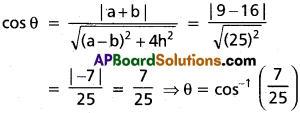
Question 5.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to be perpendicular.
Solution:
S.S₁₁ = S²₁
(x² + y² + 2gx + 2fy + c) (c) = [gx + fy + c]²
= g²x² +f²y²+ 2gfxy + 2gcx + 2fyc + c²
(gx + fy)² = c(x² + y²)
g²x² + f²y² + 2fg xy = cx² + cy²
(g² – c)x + 2fgxy + (f² – c)y² = 0
co-efficient of x² + co-efficient of y² = 0
g² – c + f² – c = 0
g² + f² = 2c

Question 6.
From a point on the circle x² + y² + 2gx + 2fy + c = 0, two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = 0 (0 < a < π/2). Prove that the angle between them is 2α.
Solution:
[x²₁ + y²₁ + 2gx₁ + 2fy₁ + c sin² α + (g² + f²) cos² α] (S)
= (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c sin² α + (g² + f²) cos² α)²
[(-c + c sin² α)+ (g² + f²) cos² α]S
= (x (x₁ + g) + y (y₁ + f) + gx₁ + fy₁ + c sin² α + (g² + f²) cos² α)²
[cos² α (g² + f² – c)] S
= [x (x₁ + g) + y (y₁ + f) + gx₁ + fy₁ + c sin² α + (g² + f²)cos² α
Let g² + f² – c = r²
= [x (x₁ + g) + y (y₁ + f) + gx₁ + fy₁ + gx₁ + fy₁ + c + (cos² α).r²)²
Coefficient of x² is r² cos² α – (x₁ + g)²
Coefficient of y² is r² cos2 α – (y₁ + f)²
Coefficient of xy is
h. cos² α r² – 2 (x₁ + g) (y₁ + f)

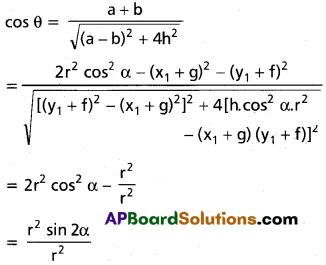
cos θ = cos 2 α
θ = 2α
Hence proved.