Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Circle Solutions Exercise 1(c) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Circle Solutions Exercise 1(c)
I.
Question 1.
Find the equation of the tangent at P of the circle S = 0 where P and S are given by
i) P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Solution:
Equation of the circle
S ≡ x² + y² – 6x + 4y – 12 = 0
Equation of the tangent at P(7, -5) is
S1 = xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
⇒ x. 7 + y(-5) – 3(x + 7) + 2(y – 5) – 12 = 0
⇒ 7x – 5y – 3x – 21 + 2y – 10 – 12 = 0
4x – 3y – 43 = 0
ii) P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Solution:
Equation of the tangent at P is
x(-1) + y . 1 – 3(x – 1) + 2(y + 1) – 12 = 0
⇒ x + y – 3x + 3 + 2y + 2 – 12 = 0
⇒ -4x + 3y – 7 = 0
⇒ 4x – 3y + 7 = 0
iii) P = (-6, -9), S ≡ x² + y² + 4x + 6y – 39
Solution:
Equation of the tangent at P is S1 =0
(i.e.,) x(-6) + y(-9) + 2(x – 6) + 3(y – 9) – 39 = 0
⇒ -6x – 9y + 2x – 12 + 3y – 27 – 39 = 0
⇒ – 4x- 6y- 78 = 0
⇒ 4x + 6y + 78 = 0
⇒ 2x + 3y + 39 = 0
iv) P = (3, 4), S ≡ x² + y² – 4x – 6y + 11
Solution:
Equation of the tangent at P is S1 = 0
⇒ x(3) + y(4) – 2 (x + 3) – 3(y + 4) + 11 =0
3x + 4y – 2x – 6 – 3y – 12 + 11 =0
x + y – 7 = 0
![]()
Question 2.
Find the equation of the normal at P of the circle S = 0 where P and S are given by
i) P = (3, -4), S ≡ x² + y² + x + y – 24
Solution:
Equation of the normal is
(x – x1) (y1 + f) – (y – y1) (x1 + g) = 0
(x – 3) (-4 + \(\frac{1}{2}\)) – (y + 4) (3 + \(\frac{1}{2}\)) = 0
–\(\frac{7}{2}\)(x – 3) – \(\frac{7}{2}\) (y + 4) = 0
⇒ (x – 3) + (y + 4) = 0
x – 3 + y + 4 = 0
x + y + 1 = 0
ii) P = (3, 5), S ≡ x² + y² – 10x – 2y + 6
Solution:
Equation of the normal is
(x – x1) (y1 + f) – (y – y1) (x1 + g) = 0
(x – 3) (5 – 1) – (y – 5) (3 – 5) = 0
4x – 12 + 2y – 10 = 0
4x + 2y – 22 = 0
or
2x + y – 11 = 0
iii) P = (1, 3), S ≡ 3(x² + y²) – 19x – 29 y + 76
Solution:
Equation of the circle is
x² + y² – \(\frac{19}{3}\)x – \(\frac{29}{3}\)y + \(\frac{76}{3}\) = 0
Equation of the normal is
(x – 1)(3 – \(\frac{29}{6}\)) – (y – 3) (1 – \(\frac{19}{6}\) ) = 0
– \(\frac{11}{6}\)(x – 1) + \(\frac{13}{6}\)(y – 3) = 0
11(x – 1) – 13(y – 3) = 0
11x – 11 – 13y + 39 = 0
11x – 13y + 28 = 0
iv) P = (1, 2), S ≡ x² + y² – 22x – 4y + 25
Solution:
Equation of the normal at P is
(x – 1) (2 – 2) – (y – 2) (1 – 11) = 0
10(y – 2) = 0 ⇒ y – 2 = 0
or y = 2
II.
Question 1.
Find the length of the chord intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3
Solution:
Equation of the circle is
S ≡ x² + y² – x + 3y – 22 = 0
Centre C(\(\frac{1}{2}\), –\(\frac{3}{2}\))

Equation of the line is y = x – 3 ⇒ x – y – 3 = 0
P distance from the centre
\(=\frac{\left|\frac{1}{2}+\frac{3}{2}-3\right|}{\sqrt{1+1}}=\frac{1}{\sqrt{2}}\)
Length of the chord = \(\sqrt{r^{2}-P^{2}}\)

Question 2.
Find the length of the chord intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0
Solution:
Equation of the circle is x² + y² – 8x – 2y – 8 = 0
Centre is C(4, 1), r = \(\sqrt{16+1+8}\) = 5
Equation of the Sine is x + y + 1 =0
P = distance from the centre = \(\frac{|4+1+1}{\sqrt{1+1}}\)
= \(\frac{6}{\sqrt{2}}=3\sqrt{2}\)
Length of the chord = 2\(\sqrt{r^{2}-P^{2}}\)
= 2\(\sqrt{25-18}\)
= 2\(\sqrt{7}\) units.
![]()
Question 3.
Find the length of the chord formed by x² + y² = a² on the line x cos α + y sin α = p.
Solution:
Equation of the circle is x² + y² = a²
Centre C(0, 0), r = a
Equation of the line is
x cos α + y sin α – p = 0
P = distance from the centre
= \(\frac{|0+0-p|}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\) = p
Length of the chord = 2\(\sqrt{r^{2}-p^{2}}\)
Question 4.
Find the equation of circle with centre (2, 3) and touching the line 3x – 4y + 1 =0.
Solution:
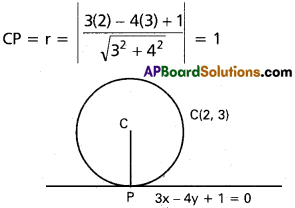
Equation of circle (x – h)² + (y – k)² = r²
(x – 2)² + (y – 3)² = 1
x² + y² – 4x – 6y + 12 = 0
Question 5.
Find the equation of the circle with centre (-3, 4) and touching y – axis.
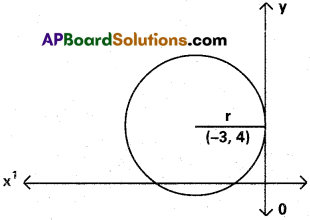
Solution:
Centre of the circle is C(-3, 4)
The circle touches y – axis
r = x co – ordinates of c = |-3| = 3
Equation of the circle is (x + 3)² + (y – 4)² = 9
x² + 6x + 9 + y² – 8y + 16 – 9 = 0
x² + y² + 6x – 8y + 16 = 0
Question 6.
Find the equation of tangents of the circle x² + y² – 8x – 2y + 12 = 0 at the points whose ordinates are 1.
Solution:
Equation of the circle is
x² + y² – 8x – 2y + 12
Suppose co – ordinates of P are (x1, 1)
P is a point on the circle
x²1 + 1 – 8x1 – 2 + 12 = 0
x²1 – 8x1 + 11 = 0
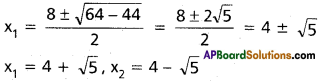
Co – ordinates of P are (4 + √5, 1) and Q(4 – √5, 1)
Equation of the tangent at P(4 + √5, 1) is
x(4 + √5) + y • 1 – 4(x + 4 + √5) – (y + 1) + 12 = 0
⇒ 4x + √5x + y – 4x – 16 – 4√5 – y – 1 + 12 = 0
⇒ √5x – 5 – 4√5 = 0 ⇒ √5 (x – √5 – 4) = 0
⇒ x – √5 – 4 = 0
x = 4 + √5
Equation of the tangent at Q(4 – √5, 1) is
⇒ x(4 – √5) + y. 1 – 4(x + 4 – √5) – (y + 1) + 12 = 0
⇒ 4x – √5x + y – 4x – 16 + 4√5 – y- 1 + 12 = 0
⇒ -√5x + 4√5 – 5 = 0
⇒ -√5 (x – 4 + √5) = 0
⇒ x – 4 + √5 = 0
x = 4 – √5
![]()
Question 7.
Find the equation of tangents of the circle x² + y² – 10 = 0 at the points whose abscissae are 1.
Solution:
Equation of the circle is x² + y² = 10
Suppose co-ordinates of P are (1, y1)
1 + y²1 = ,10 ⇒ y²1 =9
y1 = ±3
Co-ordinates of P are (1, 3) and (1, -3)
Equation of the tangent at P(1, 3) is
x. 1 + y. 3 = 10
x + 3y – 10 = 0
Equation of the tangent of P(1, -3) is
x. 1 + y(-3) = 10 ⇒ x – 3y – 10 = 0
III.
Question 1.
If x² + y² = c² and \(\frac{x}{a}+\frac{y}{b}\) = 1 intersect at A and B, then find \(\overline{\mathrm{AB}}\). Hence deduce the condition, that the line touches the circle.
Solution:
x² + y² = c²
C = (0, 0) r = c
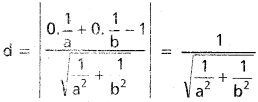
Length of chord = 2\(\sqrt{r^{2}-d^{2}}\)
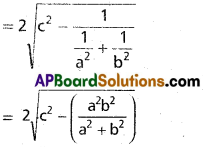
Line touches circle when r² = d² or r = d
Length of the chord = 0
c = \(\sqrt{\frac{a^2 b^2}{a^2+b^2}}\)
Question 2.
The line y = mx + c and the circle x² + y² = a² intersect at A and B. If AB = 2λ, then show that c² =(1 + m²) (a² – λ²)
Solution:
C = (0, 0) r = a
Length of chord 2\(\sqrt{r^{2}-d^{2}}\)
2\(\sqrt{r^{2}-d^{2}}\) = 2λ
r² – d² = λ²
y = mx + c ⇒ mx – y + c = 0
d = \(\frac{|0-0+c|}{\sqrt{m^{2}+1}}\)
d² = \(\frac{c^{2}}{m^{2}+1}\)
r² – d² = λ² and r = a
a² – d² = λ²
a² – λ² = d² = \(\frac{c^{2}}{m^{2}+1}\)
∴ c² = (a² – λ²) (1 + m²) is the required condition.
Question 3.
Find the equation of the circle with centre (-2, 3) cutting a chord length 2 units on 3x + 4y + 4 = 0
Solution:
Equation of the line is 3x + 4y + 4 = 0
P = Length of the perpendicular
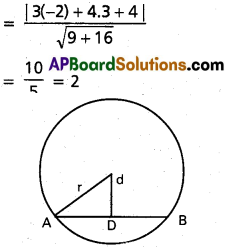
Length of the chord = 2λ = 2 ⇒ λ = 1
If r is the radius of the circle then
r² = 2² + 1² – 4 + 1 = 5
Centre of the circle is (-2, 3)
Equation of the circle is (x + 2)² + (y – 3)² = 5
x² + 4x + 4 + y² – 6y + 9 – 5 = 0
i.e., x² + y² + 4x – 6y + 8 = 0
Question 4.
Find the equation of tangent and normal at (3, 2) of the circle x² + y² – x – 3y – 4 = 0.
Solution:
Equation of the circle is x² + y² – x – 3y – 4 = 0
Equation of the tangent at P (3, 2) is
x. 3 + y. 2 – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
6x + 4y – x – 3 – 3y – 6 – 8 = 0
5x + y – 17 = 0
The normal is perpendicular to the tangent Equation of the normal can be taken as x – 5y + c = 0
The normal passes through P(3, 2)
3 – 10 + c = 0 ⇒ c = 7
Equation of the normal is x – 5y + 7 = 0
![]()
Question 5.
Find the equation of the tangent and normal at (1, 1) to the circle 2x² + 2y² – 2x – 5y + 3 = 0.
Solution:
Equation of the circle is
2x² + 2y² – 2x – 5y + 3 = 0
x² + y² – x – \(\frac{5}{2}\)y – \(\frac{3}{2}\) = 0
Equation of the tangent at P(1, 1) is
x. 1 + y.1 – \(\frac{1}{2}\)(x + 1) – \(\frac{5}{4}\)(y + 1) + \(\frac{3}{2}\) = 0
4x + 4y – 2 (x + 1) – 5(y +1) + 6 = 0
4x + 4y – 2x – 2-5y- 5 + 6 = 0
2x – y – 1 = 0
Equation of the normal can be taken as
x + 2y + k = 0
The normal passes through P(1, 1)
⇒ 1 + 2 + k = 0 ⇒ k = -3
Equation of the normal is x + 2y – 3 = 0
Question 6.
Prove that the tangent at (3, -2) of the cjrcle x² + y² = 13 touches the circle x² + y² + 2x – 10y – 26 = 0 and find its point of contact.
Solution:
Equation of the circle is x² + y² = 13
Equation of the tangent at P(3, -2) is
x. 3 + y (-2) = 13
3x – 2y – 13 = 0
Equation of the second circle is
x² + y² + 2x – 10y – 26 = 0
Centre is C(-1, 5) r = \(\sqrt{1+25+26}\)
= √52 = 2√3
P = length of the perpendicular from
![]()
= radius
∴ The tangent to the first circle also touches the second circle.
Equation of the circle is
x² + y² + 2x – 10y – 26 = 0
⇒ 3x – 2y – 13 = 0
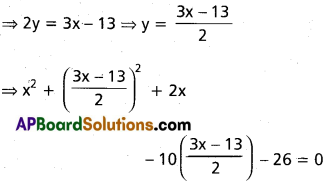
⇒ 13x² – 130 x + 325 = 0
x² – 10x + 25 = 0 ⇒ (x – 5)² = 0
x – 5 = 0 ⇒ x = 5
x = 5, y = 1 (5, 1) is point of contact
Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and also find its point of contact.
Solution:
Tangent at (-1, 2) to
x² + y² – 4x – 8y + 7 = 0 is
⇒ x(-1) + y(2) – 2(x – 1) – 4(y + 2) + 7 = 0
⇒ -3x – 2y + 1 = 0 (or) 3x + 2y – 1 = 0
If 3x + 2y – 1 = 0 is tangent to
x² + y² + 4x + 6y = 0, then radius of circle should be equal to perpendicular from centre to line 3x + 2y – 1 = 0
C: (-2, -3)
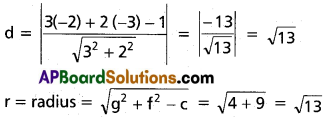
d = r
Hence 3x + 2y – 1 = 0 is also tangent to x² + y² + 4x + 6y = 0
point of contact (foot of perpendicular)
Let (h, k) be foot of perpendicular

h = 1, k = -1
(1, -1) is point of contact.
Question 8.
Find the equations of the tangents to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0. .
Solution:
Equation of the circle is
x² + y² – 4x + 6y – 12 = 0
Centre is C(2, -3); r = radius
= \(\sqrt{4+9+12}\) = 5
Equation of the given line is x + y – 8 = 0
The tangent is parallel to this line
Equation of the tangent can be taken as x + y + k = 0
Length of the perpendicular from
c = \(\frac{|2-3+k|}{\sqrt{1+1}}\)
⇒ |k – 1| = 5√2
⇒ k – 1 = ± 5√2
⇒ k = 1 ± 5√2
Equation of the required tangent is
x + y + 1 ± 5√2 = 0
![]()
Question 9.
Find the equations of the tangents to the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
x² + y² + 2x – 2y – 3 = 0, C : (-1, 1)
r = \(\sqrt{1+1+3}\) = √5
y = –\(\frac{1}{3}\)x + k is line ⊥ to 3x – y + 4 = 0
x + 3y – 3k = 0
√5 = \(\frac{|-1+3+3k|}{\sqrt{1+9}}\)
Squaring on both sides
(3k + 2)² = 50
9k² + 12k + 4 – 50 = 0
9k² + 12k – 46 = 0
k = \(\frac{-12 \pm \sqrt{144+1656}}{18}=\frac{-12 \pm 30 \sqrt{2}}{18}\)
= \(\frac{6(-2 \pm 5 \sqrt{2})}{18}\) ⇒ 3k = -2 ± 5√2
Equation of the required tangent is
x + 3y – 2 ± 5√2 = 0
Question 10.
Find the equation of the tangents to the circle x² + y² – 4x – 6y + 3 = 0 which makes an angle 45° with X – axis.
Solution:
Equation of the circle is x² + y² – 4x – 6y + 3 = 0
Centre C(2, 3), r = \(\sqrt{4+9-3}\) = √10
Slope of the tangent m = tan 45° = 1
Equation of the tangent can be taken as
y = x + c
x – y + c = 0
Length of the perpendicular from centre =

Equation of the tangents
x – y + 1 ± 2 √5 = 0
Question 11.
Find the equation of the circle passing through (-1, 0) and touching x + y – 7 = 0 at (3, 4).
Solution:
Suppose equation of the circle is
x² + y² + 2gx + 2fy + c = 0
It passes through A (-1, 0)
1 + 0 – 2g + 0 + c = 0
2g – c = 1 ……….. (1)
Equation of the tangent at P(3, 4) is
3x + 4y + g(x + 3) + f(y + 4) + c = 0
(3 + g)x + (4 + f)y + (3g + 4f + c) = 0 ………….. (2)
Given equation of the tangent is
x + y – 7 = 0 ……….. (3)
Comparing (2) and (3)

From (1)- 2 – c = 1 ⇒ c = -3
Equation of the circle is
x² + y² – 2x – 4y – 3 = 0
Question 12.
Find the equations of the circles passing through (-1, 1), touching the lines 4x + 3y + 5 = 0 and 3x – 4y – 10 = 0.
Solution:
Suppose equation of the circle is
x² + y² + 2gx + 2fy + c = 0
Let centre be (-g, -f) 1 from centre to lines be equal (radius)

Case (i):
If g = -1; f = -2
Circle is passing through (1, -1)
∴ x² + y² + 2gx + 2fy + c = 0
1 + 1 + 2g – 2f + c = 0
2 – 2 + 4 + c = 0 (or) c = – 4
Required equation of circle be
x² + y² – 2x + 4y – 4 = 0
Case (ii):

∴ Required equation of circle be
25(x² + y²) – 26x +68y + 44 = 0
![]()
Question 13.
Show that x + y + 1 =0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact.
Solution:
x² + y² – 3x + 7y + 14 = 0
![]()
Perpendicular distance from centre on x + y + 1 = 0 if equals to radius, then x + y + 1 = 0 is tangent
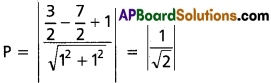
∴ x + y + 1 is tangent y = -x – 1
Substituting value of ‘y’ in equation
x² + y² – 3x + 7y + 14 = 0, We get
x² + (-x – 1)² – 3x + 7 (-x – 1) + 14 = 0
⇒ 2x² – 8x + 8 = 0
⇒ x² – 4x + 4 = 0 (or) x = 2
y – x – 1, y = -3
Point of contact is (2, -3)