Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Permutations and Combinations Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2A Permutations and Combinations Important Questions
Question 1.
If np3 = 1320, find n. (Mar. 2005)
Solution:
Hint : nPr = \(\frac{n !}{(n-r) !}\)
= n(n – 1) (n – 2) …… (n – r + 1)
∴ nP3 = 1320
= 10 × 132
= 10 × 12 × 11
= 12 × 11 × 10 = 12P3
∴ n = 12
Question 2.
If nP7 = 42. nP5, find n. (TS Mar. ’17, ’15, ’11, ’07)
Solution:
nP7 = 42. nP5
n(n – 1)(n – 2)(n – 3)(n – 4)(n – 5)(n – 6)
= 42. n(n – 1) (n – 2) (n – 3) (n – 4)
⇒ (n – 5) (n – 6) = 42
⇒ (n – 5)(n – 6) = 7 × 6
⇒ n – 5 = 7 or n – 6 = 6
∴ n = 12
![]()
Question 3.
If 10. nC2 = 3. find n. (AP Mar. ’15)
Solution:
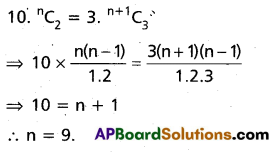
Question 4.
If 15C2r – 1 = 15C2r + 4 (Mar. ’14, ’05)
Solution:

Question 5.
If nC5 = nC6, then find 13Cn (Mar. ’13)
Solution:
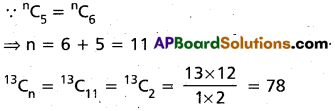
Question 6.
If nP4 = 1680, find n. (Mar. ’14; May ’06)
Solution:
Given nP4 = 1680
But nP4 = n(n – 1) (n – 2) (n -3).
Thus, we are given n(n – 1) (n – 2) (n – 3)
= 1680 = 8 × 7 × 6 × 5.
On comparing the largest integers on both sides, we get n = 8.
![]()
Question 7.
Find the number of ways of selecting 4 boys and 3 girls from a group of 8 boys and 5 girls. (TS Mar.’15)
Solution:
4 boys can be selected from the given 8 boys in 8C4 ways and 3 girls can be selected from the given 5 girls in 5C3 ways. Hence, by the Fundamental principle, the number of required selections is 8C4 x × 5C3 = 70 × 10 = 700.
Question 8.
Find the number of positive divisors of 1080. (AP Mar. ’16)
Solution:
1080 = 23 × 33 × 51.
The number of positive divisors of 1080
= (3 + 1) (3 + 1) (1 + 1)
= 4 × 4 × 2 = 32.
Question 9.
Find the number of different chains that can be prepared using 7 different coloured beads. (AP Mar. 17)
Solution:
We know that the number of circular permutations of hanging type that can be formed using n things is \(\frac{1}{2}\) {(n – 1)!}. Hence the number of chains is \(\frac{1}{2}\) {(7 – 1)’} = \(\frac{1}{2}\) (6!) = 360.
Question 10.
Find the value of 10C5 + 2. 10C4 + 10C3. (TS Mar. ’17)
Solution:
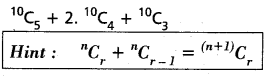
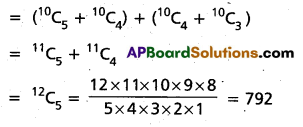
Question 11.
If (n + 1)P5 : nP6 = 2 : 7, find (Mar. ’07)
Solution:
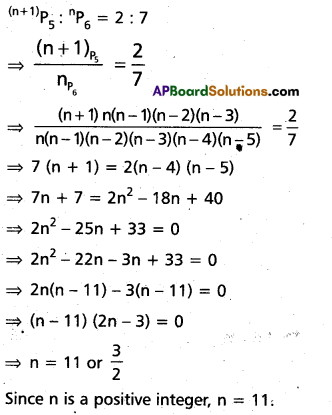
![]()
Question 12.
Find the number of ways of preparing a chain with 6 different coloured beads. (T.S Mar. ’16; May ’08)
Solution:
Hint :The number of circular permutations like the garlands of flowers, chains of beads etc., of n things = \(\frac{1}{2}\)(n – 1)!
The number of ways of preparing a chain with 6 different coloured beads.
= \(\frac{1}{2}\) (6 – 1)! = \(\frac{1}{2}\) × 5! = \(\frac{1}{2}\) × 120 = 60
Question 13.
If nPr = 5040 and nCr = 210, find n and r. (AP Mar. ‘17, ‘16)
Hint: nPr = r! nCr and
nPr = n (n – 1) (n – 2) ……. [n – (r – 1)]
Solution:

Question 14.
If 12Cr + 1 = 12C3r – 5, find r. (TS Mar. ’16, Mar. 2008)
Solution:
12Cr + 1 = 12C3r – 5
⇒ r + 1 = 3r – 5 or (r + 1) + (3r – 5) = 12
⇒ 1 + 5 = 2r or 4r – 4 = 12
⇒ 2r = 6 or 4r = 16
⇒ r = 3 or r = 4
∴ r = 3 or 4.
Question 15.
Simplify
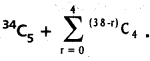 (AP Mar. ’17, ’16, ’11)
(AP Mar. ’17, ’16, ’11)
Solution:

Question 16.
Find the number of ways of selecting 3 vowels and 2 consonants from the letters of the word EQUATION. (May 11; Mar.07)
Solution:
The word EQUATION contains 5 vowels and 3 consonants.
Thè 3 vowels can be selected from 5 vowels in 5C3 = 10 ways.
The 2 consonants can be selected from 3 consonants in 3C2 = 3 ways.
∴ The required number of ways of selecting 3 vowels and 2 consonants = 1o × 3 = 30
Question 17.
Find the number of ways of selecting 11 member cricket team from 7 bats men, 6 bowlers and 2 wicket keepers so that the team contains 2 wicket keepers and atleast 4 bowlers. (mar. ’14))
Solution:
The required cricket team can have the following compositions
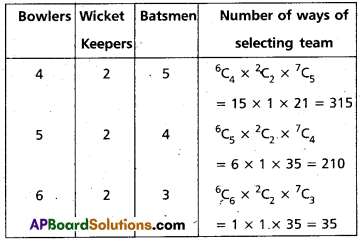
Therefore, the number of ways of selecting the required cricket team
= 315 + 210 + 35 = 560.
Question 18.
i) If 12C(s + 1) = 12C(2s – 5), then find s. (Mar.’11)
ii) If nC21 = nC27 find 49Cn. (Mar. 06; May 06)
Solution:
i) 12Cs + 1 = 1C2s – 5 ⇒ either s + 1 = 2s – 5 or s + 1 + 2s – 5 = 12
⇒ s = 6 or 3s = 16
∴ s = 6 (since s’ is a non negative integer)
ii) nC21 = nC27 ⇒ n = 21 + 27 = 48
Hence 49Cn = 49C48 = 49C1 = 49.
![]()
Question 19.
Find the sum of all 4 digited numbers that can be formed using the digits 0, 2, 4, 7, 8 without repetition. (TS Mar. ’15)
Solution:
First Method : The number of 4 digited numbers formed by using the digits 0, 2, 4, 7, 8 without repetition
= 5P4 – 4P3 = 120 – 24 = 96
Out of these 96 numbers,
4P3 – 3P2 numbers contain 2 in units place
4P3 – 3P2 numbers contain 2 in tens place
4P3 – 3P2 numbers contain 2 in hundreds place
4P3 numbers contain 2 in thousands place
∴ The value obtained by adding 2 in all the numbers
= (4P3 – 3P2) 2 + (4P3 – 3P2) 20 + (4P3 – 3P2) 200 + 4P3 × 2000
= 4P3 (2 + 20 + 200 + 2000) – 3P2 (2 + 20 + 200)
= 24 × (2222) – 6(222)
= 24 × 2 × 1111 – 6 × 2 × 111
Similarly, the value obtained by adding 4 is
24 × 4 × 1111 – 6 × 4 × 111
the value obtained by adding 7 is
24 × 7 × 1111 – 6 × 7 × 111
the value obtained by adding 8 is
24 × 8 × 1111 – 6 × 8 × 111
∴ The sum of all the numbers
= (24 × 2 × 111 – 6 × 2 × 111) + (24 × 4 × 1111 – 6 × 4 × 111) + (24 × 7 × 1111 – 6 × 7 × 111) + (24 × 8 × 1111 – 6 × 8 × 111)
= 24 × 1111 × (2 + 4 + 7 + 8) – 6 × 111 × (2 + 4 + 7 + 8)
= 26664 (21) – 666 (21)
= 21 (26664 – 666)
= 21(25998)
= 5, 45, 958.
(or) Second Method
If Zero is one among the given n digits, then the sum of the r – digited numbers that can be formed using the given ‘n’ distinct digits (r ≤ n ≤ 9) is
(n -1)P(r – 1) × sum of the digits × 111 …. 1 (r times)
– (n – 2)P(r – 2) × sum of the digits × 111 …. 1 [(r – 1) times]
Hence n = 5, n = 4, digits are {0, 2, 4, 7, 8}
Hence the sum of all 4 digited numbers that can be formed using the digits {0, 2, 4, 7, 8} without repetition is

![]()
Question 20.
If the letters of the word MASTER are permuted in all possible ways and the words thus formed are arranged in the
dictionary order, then find the ranks of the words (Mar. 11)
i) REMAST
ii) MASTER. (TS Mar. 16; AP Mar. ‘15; May ‘11, ’08, ‘07, ‘06)
Solution:
i) Thé alphabetical order of the letters of the given word is A, E, M, R, S, T
The number of words begin with A is 5!
= 120
The number of words begin with E is 5!
= 120
The number of words begin with M is 5!
= 120
The number of words begin with RA is 4!
= 24
The number of words begin with REA is 3!
= 6
The next word is REMAST
Rank of the word REMAST = 3 (120) + 24 + 6 + 1 = 360 + 31 = 391
ii) The alphabetical order of the letters of the given word is A, E, M, R, S, T
The number of words begin with A is 5!
= 120
The number of words begin with E is 5!
= 120
The number of words begin with MAE is 3!
= 6
The number of words begin with MAR is 3!
= 6
The number of words begin with MASE is 2!
= 2
The number of words begin with MASR is 2!
= 2
The next word is MASTER.
∴ Rank of the word MASTER = 2(120) + 2(6) + 2(2) + 1
= 240 + 12 + 4 + 1 = 257
Question 21.
Find the number óf ways of arranging the letters of the word. (Mar. ’11, ’06)
i) INDEPENDENCE (May ’13)
ii) MATHEMATICS (Mar. ’13) (May ’11)
iii) SINGING
iv) PERMUTATION
v) COMBINATION
vi) INTERMEDIATE
Solution:
i) The word INDEPENDENCE contains 12 letters in which there are 3 N’s are alike, 2 D’s are alike, 4 E’s are alike and rest are different.
∴ The number of required arrangements
= \(\frac{(12) !}{4 ! 3 ! 2 !}\)
ii) The word MATHEMATICS contains 11 letters in which there are 2 M’s are alike, 2 A’s are alike, 2 T’s are alike and rest are different.
∴ The number of required arrangements
= \(\frac{7 !}{2 ! 2 ! 2 !}\)
iii) The word SINGING contains 7 letters in which there are 2 l’s are alike, 2 N’s are alike, 2 G’s are alike and rest is different.
∴ The number of required arrangements
= \(\frac{(11) !}{2 !}\)
iv) The word PERMUTATION contains 11 letters in which there are 2 T’s are alike and rest are different.
∴ The number of required arràngements
= \(\frac{(11) !}{2 ! 2 ! 2 !}\)
v) The word COMBINATION contains 11 letters in which there are 2 O’s are alike, 2 l’s are alike, 2 N’s are alike and rest are different.
∴ The number of required arrangements
= \(\frac{(11) !}{2 ! 2 ! 2 !}\)
vi) The word INTERMEDIATE contains 12 letters in which thère are 2 l’s are alike, 2 l’s are alike, 3 E’s are alike and rest are different.
∴ The number of required arrangements
= \(\frac{(12) !}{2 ! 2 ! 3 !}\)
![]()
Question 22.
Prove that
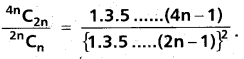
(TS Mar. ’17 AP Mar. ’15)
Solution:

Question 23.
If a set A has 12 elements, find the number of subsets of A having
(i) 4 elements
(ii) Atleast 3 elements
(iii) Atmost 3 elements. (May 2007)
Solution:
Number of elements in set A = 12 .
(i) Number of subsets of A with exactly 4 elements = 12C4 = 495
(ii) The required subset contains atleast 3 elements.
Number of subsets of A with exactly 0 elements iš 12C0,
Number of subsets of A with exactly 1 element is 12C1.
Number of subsets of A with exactly 2 element is 12C2.
Total number of subsets of A formed = 212
∴ Number of subsets of A with atleast 3 elements
= (Total number of subsets) – (number of subsets contains 0 or 1 or 2 elements)
= 212 – (12C0 + 12C1 + 12C2)
= 4096 – (1 – 12 + 66) = 4096 – 79 = 4017
(iii) The required sibset contains atmost 3 elements i.e., it may contain 0 or 1 or 2 or 3 elements.
Number of subsets of A with exactly 0 elements is. 12C0
Number of subsets of A with exactly 1 element is 12C1
Number of subsets of A with exactly 2 elements is 12C2
Number of subsets of A with exactly 3 elements is 12C3
∴ Number of subsets of A with atmost 3 elements
= 12C0 + 12C1 + 12C2 + 12C3
= 1 + 12 + 66 + 220
= 299
![]()
Question 24.
Find the number of ways of forming a committee of 5 members out of 6 Indians and 5 Americans so that always the Indians will be in majority in the committee. (TS Mar. ’15, ’13, ’08)
Solution:
Since committee contains majority of Indians, the members of the committee may be of the following types.

The number of selections in type I
= 6C5 × 5C0 = 6 × 1 = 6
The number of selections in type II
= 6C4 × 5C1 = 15 × 5 = 75
The number of selections in type III
= 6C3 × 5C2 = 20 10 = 200
= 6C3 × 5C2 = 20 10 = 200
∴ The required number ways of selecting a committee = 6 + 75 + 200 = 281.
Question 25.
If the letter of the word PRISON are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word. PRISON (AP Mar. ’17 Mar. ‘14, ’05; May ’13)
Solution:
The letters of the given word in dictionary order are
I N O P R S
In the dictionary order, first all the words that begin with I come. If I occupies the first place then the remaining 5 places can be filled with the remaining 5 letters in 5! ways. Thus, there are 5 number of words that begin with I. On proceeding like this we get

Hence the rank of PRISON is
3 × 5! + 3 × 4! + 2 × 2! + 1 × 1
= 360 + 72 + 4 + 1 + 1 = 438.
Question 26.
Find the sum of all 4- digited numbers that can be formed using the digits 1, 3, 5, 7, 9. (Mar. ’13)
Solution:
We know that the number of 4 digited numbers that can be formed using the digits
1, 3, 5, 7, 9 is 5P4 = 120.
We have to find their sum. We first find the sum of the digits in the unitš place of all the 120 numbers. Put 1 in the units place.
![]()
The rerpaining 3 places can be filled with the remaining 4 digits in 4P3 ways. Which means that there are 4P3 number of 4 digited numbers with 1 in the units place. Similarly, each of the other digits 3, 5, 7, 9 appears in the units pläce 4P3 times. Hence, by adding all these digits of the units place, we get the sum of the digits in the units place.
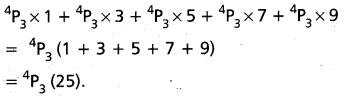
Similarly, we get the sum of all digits in 10’s place also as 4P3 × 25. Since it is in 10’s place, its value is
4P3 × 25 × 10.
Like this the values of the sumof the digits in 100’s place and 1000’s place are respectively
4P3 × 25 × 100 and 4P3 × 25 × 1000.
On adding all these sums, we get the sum of all the 4 digited numbers formed by using the digits 1, 3, 5, 7, 9. Hence the required sum is

![]()
Question 27.
If the letters of the word EAMCET are permuted in all possible ways and if the words thus formed are arranged in the dictionary order, find the rank of the word EAMCET. (AP Mar. 16) (TS Mar. 17)
Solution:
The dictionary order of the letters of the word EAMCET is
A C E E M T
In the dictionary order first gives the words which begin with the letter A.
If we fill the first place with A, remaining 5 letters can be arranged in \(\frac{5 !}{2 !}\) ways (since there are 2 E’s) on proceeding like this, we get

Question 28.
If \({ }^{\mathrm{n}} \mathrm{P}_{4}\) = 1680, find n. (Mar. ’14, May ’06)
Solution:
Given \({ }^{\mathrm{n}} \mathrm{P}_{4}\) = 1680
But \({ }^{\mathrm{n}} \mathrm{P}_{4}\) = n(n – 1) (n – 2) (n – 3).
Thus, we are given n(n – 1) (n – 2) (n – 3)
= 1680 = 8 × 7 × 6 × 5.
On comparing the largest integers on bothsides, we get n = 8.
Question 29.
If \({ }^{12} \mathrm{P}_{r}\) = 1320, find r.
Solution:
1320 = 12 × 11 × 10 = \({ }^{12} \mathrm{P}_{3}\), Hence r = 3.
Question 30.
If (n + 1)P5 : nP5 = 3 : 2, find n
Solution:

It can be verified that n = 14 satisfies the given equation.
Question 31.
If 56P(r + 3) = 30800 : 1, find r.
Solution:
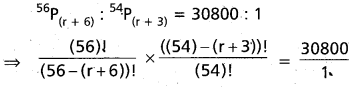
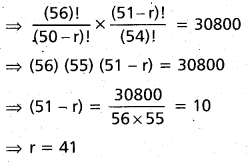
It can be verified that r given equation.
Question 32.
In how many ways 9 mathematics papers can be arranged so that the best and the worst
(i) may come together
(ii) may not come together ?
Solution:
i) If the best and worst papers are treated as one unit, then we have 9 – 2 + 1 = 7 + 1 = 8 papers. Now these can be arranged in (7 + 1) ! ways and the best and worst papers between themselves can be permuted in 2! ways. Therefore the number of arrangements in which best and worst papers come together is 8! 2!.
ii) Total number of ways of arranging 9 mathematics papers is 9!. The best and worst papers come together in 8! 2! ways. Therefore the number of ways they may not come together is 9! – 8! 2! = 8! (9 – 2) = 8! × 7.
![]()
Question 33.
Find the number of ways of arranging 6 boys and 6 girls in a row. In how many of these arrangements.
i) all the girls are together
ii) no two girls are together
iii) boys and girls come alternately ?
Solution:
i) 6 boys and 6 girls are altogether 12 persons. They can be arranged in a row in (12)! ways. Treat the 6 girls as one unit. Then we have 6 boys and 1 unit of girls. They can be arranged in 7! ways. Now, the 6 girls can be arranged among themselves in 6! ways. Thus the number of ways in which all 6 girls are together is (7! × 6!).
ii) First arrange the 6 boys in a row in 6! ways. Then we can find 7 gaps between them
(including the beginning gap and the ending gap) as shown below by the letter x :
![]()
Thus we have 7 gaps and 6 girls. They can be arranged in 7P6 ways.
Hence, the number of arrangements which no two girls sit together is 6! × 7P6 = 7.6!. 6!.
iii) The row may begin with either a boy or a girl, that is, 2 ways. If it begins with a boy, then odd places will be occupied by boys and even places by girls. The 6 boys can be arranged in 6 odd places in 6! ways and 6 girls in the 6 even places in 6! ways. Thus the number of arrangements in which boys and girls come alternately is 2 × 6! × 6!.
Question 34.
Find the number of 4 – letter words that can be formed using the letters erf the word. MIRACLE. How many of them
i) begin with an vowel
ii) begin and end with vowels
iii) end with a consonant ?
Solution:
The word MIRACLE has 7 letters. The number of 4 letter words that can be formed using these letters = 7P4 = 7 × 6 × 5 × 4 = 840
Now take 4 blanks
![]()
i) We can fill the first place with one of the 3 vowels {A, E, 1} in 3P1 = 3 ways.
Now the remaining 3 places can be filled using the remaining 6 letters in 6P3 = 6 × 5 × 4 = 120 ways.
∴ The number of 4 letter words that begin with an vowel = 3 × 120 = 360 ways.
ii) Fill the first and last places with 2 vowels in 3P2 = 3 × 2 = 6 ways.
The remaining 2 places can be filled with the remaining 5 letters in 5P2 = 5 × 4 = 20 ways.
∴ The number of 4 letter words that begin and end with vowels = 6 × 20 = 120 ways.
iii) We can fill the last place with one of the 4 consonants {C, L, R, M} in 4P1 = 4 ways. The remaining 3 places can be filled with the remaining 6 letters in 6P3 = 6 × 5 × 4 = 120 ways.
∴ The number of 4 letter words that end with a consonant is = 4 × 120 = 480 ways.
![]()
Question 35.
Find the number of ways of permuting the letters of the word PICTURE so that
i) all vowels come together
ii) no two vowels come together
iii) the relative positions of vowels and consonants are not distributed.
Solution:
The word PICTURE has 3 vowels {E, I, U} and 4 consonants {C, P, R, T}
i) Treat the 3 vowels as one unit. Then we can arrange 4 consonants + 1 unit of vowels in 5! ways. Now 3 vowels among themselves can be permuted in 3! ways. Hence the number of permutations in which 3 vowels come together.
= 5! × 3! = 120 × 6 = 720 ways.
ii) No two vowels come together First arrange the 4 consonants in 4! ways. Then in between the vowels, in the beginning and in the ending, there are 5 gaps as shown below by the x letter
![]()
In these 5 places we can arrange 3 vowels in 5P3 ways.
∴ The number of words in which no two vowels come together
= 4! × 5P3
= 24 × 5 × 4 × 3 = 1440 ways.
iii) The three vowels can be arranged in their relative positions in 3! ways and the 4 consonants can be arranged in their relative positrons in 4! ways.
![]()
The required number of arrangements is 3! 4! = 144
Question 36.
If the letters of the word PRISON are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word. PRISON (Mar. ’14, ’05; May. ’13)
Solution:
The letters of the given word in dictionary order are
I N O P R S
In the dictionary order, first all the words that begin with I come. If I occupies the first place then the remaining 5 places can be filled with the remaining 5 letters in 5! ways. Thus, there are 5! number of words that begin with I. On proceeding like this we get

Question 37.
Find the number of 4-digit numbers that can be formed using the digits 2, 3, 5, 6, 8 (without repetition). How many of them are divisible by
(i) 2
(ii) 3
(iii) 4
(iv) 5
(v) 25
Solution:
The number of 4-digit numbers that can be formed using the 5 digits 2, 3, 5, 6, 8 is 5P4 = 120
i) Divisible by 2 : For a number to be divisible by 2, the units place should befilled with an even digit. This can be done in 3 ways (2 or 6 or 8).
![]()
Now, the remaining 3 places can be filled with the remaining 4 digits in 4P3 = 24 ways.
Hence, the number of 4 – digit numbers divisible by 2 is 3 × 24 = 72.
ii) Divisible by 3 : A number is divisible by 3 if the sum of the digits n it is a multiple of 3. Since the sum of the given 5 digits is 24, we have to leave either 3 or 6 and use the digits 2, 5, 6, 8 or 2, 3, 5, 8. In each case, we can permute them in 4! ways. Thus the number of 4-digit numbers divisible by 3 is
2 × 4! 48.
iii) Divisible by 4 : A number is divisible by 4 if the number formed by the digits in the last two places (tens and units places) is a multiple of 4;
![]()
Thus we fill the last two places (as shown in the figure) with one of
28, 32, 36, 52, 56, 68
That is done in 6 ways. After filling the last two places, we can fill the remaining two places with the remaining 3 digits in
3P2 = 6 ways.
Thus, the number of 4-digit numbers divisible by 4 is 6 × 6 = 36.
iv) Divisible by 5 : After filling the units place with 5 (one way), the remaining 3 places can be filld with the remaining 4 digits in 4P3 = 24 ways. Hence the number of 4-digit numbers divisible by 5 is 24.
v) Divisible by 25 : Here also we have to fill the last two places (that is, units and tens place) with 25 (one way) as shown below.
![]()
Now the remaining 2 places can be filled with the remaining 3 digits in 3P2 = 6 ways.
Hence the number of 4 – digit numbers divisible by 25 is 6.
Question 38.
Find the sum of all 4- digited numbers that can be formed using the digits 1, 3, 5, 7, 9. (Mar ‘13)
Solution:
We know that the number of 4 digited numbers that can be formed using the digits
1, 3, 5, 7, 9 is 5P4 = 120.
We have to find their sum. We first find the sum of the digits in the units place of all the 120 numbers. Put 1 in the units place.
![]()
The remaining 3 places can be filled with the remaining 4 digits in 4P3 ways. Which means that there are 4P3 number of 4 digited numbers with 1 in the units place. Similarly, each of the other digits 3, 5, 7, 9 appears in the units place 4P3 times. Hence, by adding all these digits of the units place, we get the sum of the digits in the units place.
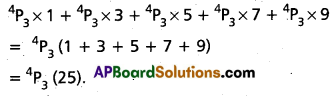
Similarly, we get the sum of all digits in 10’s place also as 4P3 × 25. Since it is in 10’s place, its value is
4P3 × 25 × 10.
Like this the values of the sum of the digits in 100’s place and 1000‘s place are respectively
4P3 × 25 × 100 and 4P3 × 25 × 1000.
On adding all these sums, we get the sum of all the 4 digited numbers formed by using the digits 1, 3, 5, 7, 9. Hence the required sum is

Question 39.
How many four digited numbers can be formed using the digits 1, 2, 5, 7, 8, 9 ? How many of them begin with 9 and end with 2 ?
Solution:
The number of four digited numbers that can be formed using the given digits 1, 2, 5, 7, 8, 9, is 6P4 = 360. Now, the first place and last place can be filled with 9 and 2 in one way.
![]()
The remaining 2 places can be filled by the remaining 4 digits 1, 5, 7, 8. Therefore these two places can be filled in 4P2 ways. Hence, the required number of ways 1. 4P2 = 12.
![]()
Question 40.
Find the number of injections of a set A with 5 elements to a set B with 7 elements.
Solution:
If a setA has m elements and the set B has n elements (m ≤ n), then the number of injections from A into B = nPm
∴ The number of injections from set A with 5 elements into set B with 7 elements.
= 7P5 = 2,520.
Question 41.
Find the number of ways in which 4 letters can be put in 4 addressed envelopes so that no letter goes into the envelope meant for it.
Solution:
Required number of ways is 4! \(\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\)
= 12 – 4 + 1 = 9
Question 42.
Find the number of 5 letter words that can be formed using the letters of the word ‘MIXTURE’ which begin with an
vowel when repetitions are allowed.
Solution:
The word MIXTURE has 7 letters 3 vowels {E, I, U} and 4 consonants {E, M, R, X} we have to fill up 5 blanks.
![]()
Fill the first place with one of the 3 vowels in 3 ways.
Each of the remain 4 places can be filled in 7 ways (since repetition is allowed)
∴ The number of 5 letter words
= 3 × 7 × 7 × 7 × 7 = 3 × 74
Question 43.
a) Find the number of functions from a set A with m elements to a set B with n elements.
Solution:
Let A = {a1, a2, ………. am} and
B = {b1, b2, …., bn}.
First, to define the image of a1 we have n choices (any element of B). Then to define the image of a2 we again have n choices (since a1, a2 can have the same image). Thus we have n choices for the image of each of the m elements of the set A. Therefore, the number of different ways of defining the images of elements of A (with images in B) is n × n × …. × n(m times) = nm.
b) Find the number of surjections from a set A with n elements to a set B with 2 elements when n > 1.
Solution:
Let A {a1, a2,….., an} and b = {x, y}. The total number of functions from A to B is 2n For a surjection, both the elements x, y of B must be in the range. Therefore, a function is not a surjection if the range contains only x (or y). There are only two such functions.
Hence, the number of surjections from A to B is 2n – 2.
Question 44.
Find the number of permutations of 4- digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6 when repetition is allowed.
Solution:

The number of permutations of 4 digit numbers that can be formed using the given 6 digits = 6 × 6 × 6 × 6 = 64 = 1,296
Question 45.
Find the number of 4- digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6 that are divisible by
(i) 2
(ii) 3 when repetition is allowed.
Solution:
(i) Numbers divisible by 2
Take 4 blank palces. First the units place
![]()
can be filled by an even digit in 3 ways (2 or 4 or 6). The remaining three places can be filled with the 6 digits in 6 ways each. Thus they can be filled in 6 × 6 × 6 = 6 ways.
Therefore, the number of 4 digited numbers divisible by 2 is 3 × 63 = 3 × 216 = 648
ii) Numbers divisible by 3
First we fill up the first 3 places with the given 6 digits in 6 ways.
![]()
After filling up the first 3 places, if we fill the units place with the given 6 digits, we get 6 consecutive positive integers. Out of these six consecutive integers exactly 2 will be divisible by ‘3’. Hence the units place can be filled in ‘2’ ways. Therefore, the number of 4 digited numbers divisible by 3.
= 63 × 2 = 216 × 2 = 432.
![]()
Question 46.
Find the number of 5 – letter words that can be formed using the letters of the word EXPLAIN that begin and end with a vowel when repetitions are allowed.
Solution:
We can fill the first and last places with vowels each in 3 ways. (E or A or I)
![]()
Now each of the remaining 3 places can be filled in 7 ways (using any letter of given 7 letters). Hence the number of 5 letter words
which begin and end with vowels ¡s
= 32 × 73 = 9 × 343 = 3087
Question 47.
Find the number of ways of arranging the letters of the word SINGING só that
i) they begin and end with I
ii) the two G’s come together .
iii) relative positions of vowels and consonants are not disturbed.
Solution:
The word SINGING has 2 I’s, 2 G’s and 2 N’s and one S. Total 7 letters.
![]()
i) First, we fill the first and last places with I’s in \(\frac{2 !}{2 !}\) = 1 way as shown below.
Now we fill the remaining 5 places with the remaining 5 letters in \(\frac{5 !}{2 ! 2 !}\) = 30 ways.
Hence the number of required permutations = 30
ii) Treat two G’s as one unit. Then we have 5 letters 2 I’s, 2 N’s and one S + one unit of 2
G’s = 6 can be arranged in \(\frac{6 !}{2 ! 2 !}\) = \(\frac{720}{2 \times 2}\)
= 180 ways.
Now the two G’s among themselves can be arranged in one way. Hence the number of received permutations = 180 × 1 = 180.
Question 48.
Find the number of ways of arranging the letters of the word a4 b3 c5 in its expanded form.
Solution:
The expanded form of a4 b3 c5 is
aaaa bbb ccccc
There are 4 + 3 + 5 = 12 letters
They can be arranged in \(\frac{(12) !}{4 ! 3 ! 5 !}\) ways.
![]()
Question 49.
If the letters of the word EAMCET are permuted in all possible ways and if the words thus formed are arranged in the dictionary order, find the rank of the word EAMCET. (A.P. Mar. ’16)
Solution:
The dictionary order of the letters of the word EAMCET is
A C E E M T
In,the dictionary order first gives the words which begin with the letter A.
If we fill the first place with A, remaining 5 letters can be arranged in \(\frac{5 !}{2 !}\) ways (since there
are 2 E’s) on proceeding like this, we get

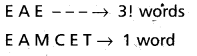
Hence the rank of the word EAMCET is
= 2 × \(\frac{5 !}{2 !}\) + 2 × 3! + 1
= 120 + 12 + 1 = 133
Question 50.
Find the number of ways of arranging 8 men and 4 women around a circular table. In how many of them
i) all the women come together
ii) no two women come together
Solution:
’Total number of persons = 12 (8 men + 4 women)
Therefore, the number of circular permutations is (11) !
i) Treat the 4 women as one unit. Then we have 8 men + 1 unit of women = 9 entities
which can be arranged around a circle in 8! ways. Now, the 4 women among themselves can be arranged in 4! ways. Thus, the number of required arrangements is 8! × 4!.
ii) First arrange 8 men around a circle in 7! ways. Then there are 8 places in between them as shown in. fig by the symbol x (one place in between any two consecutive men).
Now, the 4 women can be arranged in these 8 places in 8P4 ways.
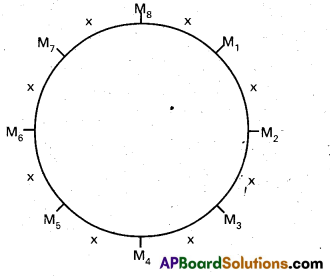
Therefore, the number of circular arrangements in which no two women come together is 7! × 8P4.
Question 51.
Find the number of ways of seating 5 Indians, 4 Americans and 3 Russians at a round table so that
i) all Indians sit together
ii) no two Russians sit together
iii) persons of same nationality sit together.
Solution:
i) Treat the 5 Indians as a single unit. Then we have 4 Americans, 3 Russians and 1 unit of Indians. That is, 8 entities in total. Which can be arranged at a round table in (8-1)! = 7! ways.
Now, the 5 Indians among themselves can be arranged in 5! ways. Hence, the number of required arrangements is 7! × 5!
ii) First we arrange the 5 Indians + 4 Americans around the table in (9 – 1) ! = 8! ways.
Now, we can find 9 gaps in between these 9 persons (one gap between any two consecutive persons).
The 3 Russians can be arranged in these 9 gaps in 9P3 ways. Hence, the number of required arrangements is 8! × 9P3.
iii) Treat the 5 Indians as one unit, the 4 Americans as the second unit and the 3 Russians as the third unit. These 3 units can be arranged at round table in (3 – 1)! = 2! ways.
Now, the 5 Indians among themselves can be permuted in 5! ways. Similarly, the 4 Americans in 4! ways and the 3 Russians in 3! ways. Hence the number of required arrangements is 2! × 5! × 4! × 3!
Question 52.
Find the number of different chains that can be prepared using 7 different coloured beads.
Solution:
We know that the number of circular permutations of hanging type that can be formed using n things is \(\frac{1}{2}\) {(n – 1)!}. Hence the number of chains is \(\frac{1}{2}\) {(7 – 1)}{
= \(\frac{1}{2}\) (6!) = 360.
Question 53.
Find the number of different ways of preparing a garland using 7 distinct red roses and 4 distinct yellow roses such that no two yellow roses come together.
Solution:
First arrange 7 red roses in a circular form (garland form) in (7 – 1)! = 6! ways. Now, there are 7 gaps and 4 yellow roses can be arranged in these 7 gaps in 4 7P4 ways.
Thus, the total number of circular permutations is 6! × 7P4.
But, in the case of garlands, clock-wise and anti-clock-wise arrangements look alike. Hence, the number of required ways is.
\(\frac{1}{2}\) (6! × 7P4)
Question 54.
14 persons are seated at a round table. Find the number of ways of selecting two persons out of them who are not seated adjacent to each other.
Solution:
The seating arrangement of given 14 persons at the round table as shown below.
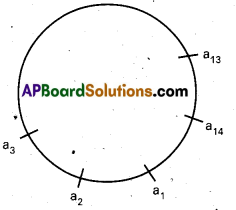
Number of ways of selecting 2 persons out of 14 persons = 14C2 = \(\frac{14 \times 13}{1 \times 2}\) = 91.
In the above arrangement two persons sitting adjacent to each other can be selected in 14 ways. (they are a1 a2, a2 a3 , a13 a14, a14 a1)
∴ The required no.of ways = 91 – 14 = 77
![]()
Question 55.
Find the number of ways of selecting 4 boys and 3 girls from a group of 8 boys and 5 girls. (T.S. Mar. ’15)
Solution:
4 boys can be selected from the given 8 boys in 8C4 ways and 3 girls can be selected from the given 5 girls in 5C3 ways. Hence, by the Fundamental principle, the number of required selections is
8C4 × 5C3 = 70 × 10 = 700.
Question 56.
Find the number of ways of selecting 4 English, 3 Telugu and 2 Hindi books out of 7 English, 6 Telugu and 5 Hindi books.
Solution:
The number of ways of selecting
4 English books out of 7 books = 7C4
3 Telugu books out of 6 books = 6C3
2 Hindi books out of 5 books = 5C2
Hence, the number of required ways
7C4 × 6C3 × 5C2 = 35 × 20 × 10 = 7000.
Question 57.
Find the number of ways of forming a committee of 4 members out of 6 boys and 4 girls such that there is atleast one girl in the committee.
Solution:
The number of ways of forming a committee of 4 members out of 10 members (6 boys + 4 girls) is 10C4. Out of these, the number of waýs of forming the committee, having no girl is 6C4 (We select all 4 members from boys).
Therefore, the number of ways of forming the committees having atleast one girl is
10C4 – 6C4 = 210 – 15 = 195.
Question 58.
Find the number of ways of selecting 11 member cricket team from 7 bats men, 6 bowlers and 2 wicket keepers so that the team contains 2 wicket keepers and atleast 4 bowlers. (Mar. 14)
Solution:
The required cricket team can have the following compositions
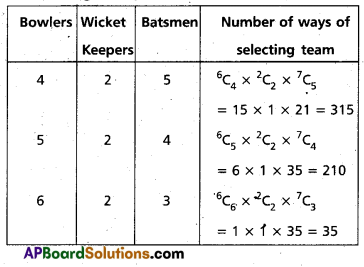
Therefore, the number of ways of selecting the required cricket team
= 315 + 210 + 35 = 560.
Question 59.
If a set of ‘n’ parallel lines intersect another set of ‘n’ parallel lines (not parallel to the lines in the first set), then find the number of parallellograms formed in this lattice structure.
Solution:
To form a parallelogram, we hâve to select 2 lines from the first set which can be done in mC2 ways and 2 lines from the second set which can be done in nC2 ways. Thus, The number of parallelograms formed is mC2 × nC2.
Question 60.
There are m points in a plane out of which p points are collinear and no three of the points are collinear unless all the three are from these p points. Find the number of different
i) straight lines passing through pairs of distinct points.
ii) triangles formed by joining these points (by line segments).
Solution:
i) From the given m points, by drawing straight lines passing through 2 distinct points at a time, we are supposed to get mC2 number of lines. But, since p out of these m points are collinear, by forming lines passing through these p points 2 at a time we get only one line instead of getting PC2. Therefore, the number of different lines passing through pairs of distinct points is
mC2 – PC2 + 1
ii) From the given m points, by joining 3 points at a time, we are supposed to get mC3 number of triangles. Since p out of these m points are collinear by joining these p points 3 at a time we do not get any triangle when as we are supposed to get PC3 number of triangles. Hence the number of triangles formed by joining the given m points
= mC2 – PC3
![]()
Question 61.
A teacher wants to take 10 students to a park. He can take exactly 3 students at a time and will not take the same group of 3 students more than once. Find the number of times
(i) each student can go to the park
(ii) the teacher can go to the park.
Solution:
i) To find the number of times a specific student can go to the park, we have to select 2 more students from the remaining 9 students. This can be done in 9C2 ways.
Hence each student can go to the park 9C2 times = \(\frac{9 \times 8}{1 \times 2}\) = 36 times
ii) The no.of times the teacher can go to park = The no.of different ways of selecting 3 students out of 10 = 10C3 = 120.
Question 62.
A double decker minibus has 8 seats in the lower deck and 10 seats in the upper deck. Find the number of ways of
arranging 18 persons in the bus if 3 children want to go to the upper deck and 4 old people can not go to the upper deck.
Solution:
Allowing 3 children to the upper deck and 4 old people to the lower deck, we are left with 11 people and 11 seats (7 seats in the upper deck and 4 in the lower deck). We can select 7 people for the upper deck out 11 people in 11C7 ways. The remaining 4 persons go to the lower deck.
Now we-can arrange 10 persons (3 children and 7 others) in the upper deck and 8 persons (4 old people and 4 others) in the lower deck in (10)! and (8)! ways respectively. Hence the required number of arrangements = 11C7 × 10! × 8!
Question 63.
Prove that
i) 10C3 + 10C6 = 11C4
ii)
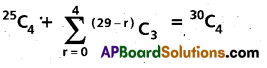
Solution:

Question 64.
i) If 12C(s + 1) = 12C(2s – 5), then find s. (Mar. ‘11)
ii) If nC21 = nC27 find 49Cn. (Mar. ‘06; May 06)
Solution:
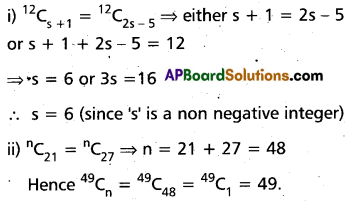
Question 65.
If there are 5 alike pens, 6 alike pencils and 7 alike erasers, find the number of ways of selecting any number of (one or more) things out of them.
Solution:
The required number of ways
= (5 + 1 (6 + 1) (7 + 1) – 1 = 335.
Question 66.
Find the number of positive divisors of 1080. (AP. Mar.’16)
Solution:
1080 = 23 × 33 × 51.
∴ The number of positive divisors of 1080
= (3 + 1) (3 + 1) (1 + 1)
= 4 × 4 × 2 = 32.