Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A De Moivre’s Theorem Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2A De Moivre’s Theorem Important Questions
Question 1.
Find the value of (1 – i)8 (Mar. ’07)
Solution:

Question 2.
If x = cis θ, then find the value of [x6 + \(\frac{1}{x^{6}}\)]
Solution:
∵ x = cos θ + i sin θ
⇒ x6 = (cos θ + i sin θ)6
= cos 6θ + i sin 6θ
⇒ \(\frac{1}{x^{6}}\) = cos 6θ – i sin 6θ
∴ x6 + \(\frac{1}{x^{6}}\) = 2 cos 6θ
![]()
Question 3.
If A, B, C are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find the value of XYZ. (AP Mar. ‘16, ’15)
Solution:
∴ A, B, C are angles of a triangle
⇒ A + B + C = 180° ——- (1)
x = cis A, y = cis B, Z = cis C
⇒ xyz = cis(A + B + C)
= cos(A + B + C) + i sin(A + B + C)
= cos(180°) + i sin (180°) .
= -1 + i(0) = -1
∴ xyz = -1
Question 4.
If 1, ω, ω2 are the cube roots of unity, then prove that \(\frac{1}{2+\omega}\) – \(\frac{1}{1+2 \omega}\) = \(\frac{1}{1+\omega}\)
Solution:
ω is a cube root of unity
1 + ω + ω2 = 0 and ω3 = 1
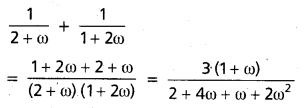

Question 5.
(2 – ω) (2 – ω2) (2 – ω10) (2 – w11) = 49. (TS Mar. ’17)
Solution:
∵ 1, ω, ω2 are the cube roots of unity,
ω3 = 1 and 1 + ω + ω2 = 0
2 – ω10 = 2 – ω9 . ω
= 2 – (ω3)3 . ω2
= 2 – (1)3 ω2 = 2 – ω2
(2 – ω)(2 – ω2) = 4 – 2ω – 2ω2 + ω3
= 4 – 2(ω + ω2) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1 = 7
∴ (2 – ω)(2 – ω2)(2 – ω10)(2 – ω11)
= (2 – ω) (2 – ω2) (2 – ω) (2 – ω2)
= ((2 – ω) (2 – ω2))2
= 72 = 49
Question 6.
If α, β are the roots of the equation x2 – 2x + 4 = 0 then for any n ∈ N show that αn + βn = 2n + 1 cos \(\left(\frac{n \pi}{3}\right)\) (Mar. ’14)
Solution:


![]()
Question 7.
Show that one value of
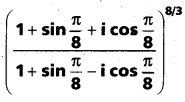
is -1.
Solution:

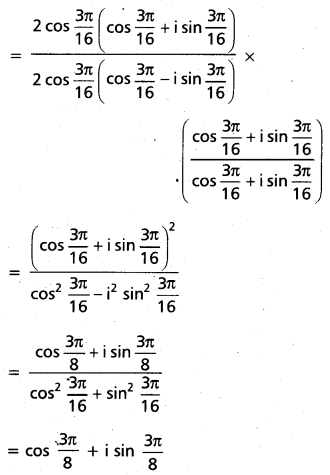
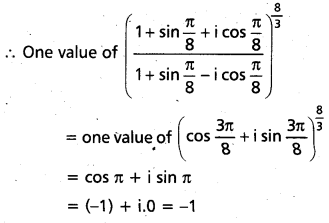
Question 8.
If n is a positive integer, show that (1 + i)n + (1 – i)n = 2\(\frac{n+2}{2}\) cos \(\left(\frac{\mathrm{n} \pi}{4}\right)\). (A.P) (Mar. ’15)
Solution:

![]()
Question 9.
If n is an integer then show that (1 + cos θ + i sin θ)n + (1 + cos θ – i sin θ)n = 2n + 1 cosn (θ/2) cos \(\left(\frac{n \theta}{2}\right)\) (May. ’11) (TS & AP Mar. ’17)
Solution:
L.H.S.
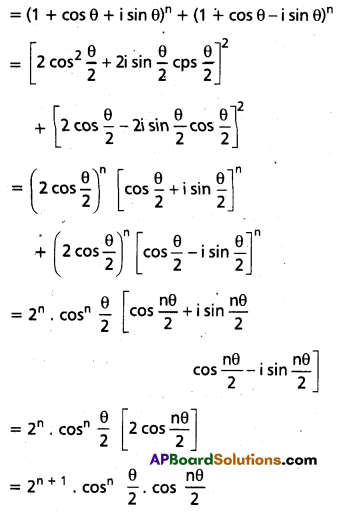
Question 10.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ. Prove that cos2 α + cos2 β + cos2 γ = \(\frac{3}{2}\) = sin2 α + sin2 β + 2 γ. (AP. Mar. ’16; TS Mar. ’15, ‘13)
Solution:
Let x = cos α + i sin α
y = cos β + i sin β
z = cos γ + i sin γ
∴ x + y + z = (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 + i. 0 = 0
(x + y + z)2 = 0
⇒ x2 + y2 + z2 + 2(xy + yz + zx) = 0
x2 + y2 + z2 = -2(xy + yz + zx)
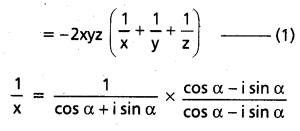

-i(sin α + sin β + sin γ) = 0 – i. 0 = 0
Substituting in (1)
x2 + y2 + z2 = 0.
(cos α + i sin α)2 + (cos β + i sin β)2 + (cos γ + i sinγ)2 = 0
(cos 2α + i sin 2α) + (cos β + i sin 2β) + (cos 2γ + i sin 2γ) = 0
(cos 2α + cos 2β + cos 2γ) + i (sin 2α + sin 2β + sin 2γ) = 0
Equating real parts
cos 2α + cos 2β + cos 2γ = 0
2cos2α – 1 + 2 cos2β – 1 + 2 cos2γ – 1 = 0
2 (cos2α + cos2β + cos2γ) = 3
cos2α + cos2β + cos2γ = \(\frac{3}{2}\)
∵ 2α + cos2β + cos2γ = \(\frac{3}{2}\)
⇒ (1 – sin2α) + (1 – sin2β) + (1 – sin2γ) = \(\frac{3}{2}\)
⇒ sin2α + sin2β + sin2γ = \(\frac{3}{2}\)
∴ cos2α + cos2β + cos2γ = \(\frac{3}{2}\)
= sin2α + sin2β + sin2β
Question 11.
If 1, ω, ω2 are the cube roots of unity prove that
i) (1 – ω + ω2)6 + (1 – ω2 + ω)6 = 128
= (1 – ω + ω2)7 + (1 + ω – ω2)7
ii) (a + b) (aω + bω2) (aω2 + bω) = a3 + b3
iii) x2 + 4x + 7 = 0 where x = ω – ω2 – 2.
Solution:
∵ 1, ω, ω2 are the cube roots of unity
⇒ 1 + ω + ω2 = 0 and ω3 = 1
i) (1 – ω + ω2)6 + (1 – ω2 + ω)6
= (-ω – ω)6 + (-ω2 – ω2)6
= (-2ω)6 + (-2ω2)6
= 26(ω6 + ω12)
= 26(1 + 1) = 26 × 2 = 27 = 128
Again (1 – ω + ω2)7 + (1 + ω – ω2)7
= (1 + ω2 – ω)7 + (1 + ω – ω2)7
= ( -ω – ω)7 + (-ω2 – ω2)7
= (-2ω)7 + (-2ω2)7
= (-2)7 (ω7 + ω14)
= (-2)7 (ω + ω2)
= -(2)7 (-1)
= 27 = 128
ii) (a+b) (a]ω + bω2)(aω2 + bω) (AP) (Mar. ’17)
Solution:
= (a + b) [a2ω3 + abω4)4 + abω2 + b2ω3]
= (a + b) [a2 + ab(ω2 + ω4) + b2]
= (a + b) [a2 + ab(ω2 + ω) + b2]
= (a + b) (a2 – ab + b2) = a3 + b3
![]()
iii) x = ω – ω2 – 2
⇒ x + 2 = ω – ω2
⇒ (x + 2)2 = ω2 + ω4 – 2ω3
⇒ x2 + 4x + 4 = ω2 + ω – 2
⇒ x2 + 4x + 4 = (-1) – 2 = -3
⇒ x2 + 4x + 7 = 0
Question 12.
Simplify \(\frac{(\cos \alpha+i \sin \alpha)^{4}}{(\sin \beta+i \cos \beta)^{8}}\)
Solution:
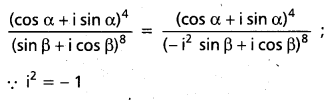
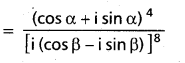
= (cos α + i sin α)4 (cos β – i sin β)-8 [i8 = (i2)4 = (-1)4 = 1]
= (cos 4α + i sin 4α) (cos 8β + i sin 8β)
= cos (4α + 8β) + i sin (4α + 8β)
Question 13.
If m, n are integers and x = cos α + i sin α, y = cos β + i sin β, then prove that
xm yn + \(\frac{1}{x^{m} y^{n}}\) = 2 cos (mα + nβ) and
xm yn – \(\frac{1}{x^{m} y^{n}}\) = 2i sin (mα + nβ).
Solution:
∵ x = cos α + i sin α, y = cos β + i sin β
⇒ xm = (cos α + i sin α)m = cos mα + i sin mα
yn = (cos β + i sin β)n = cos nβ + i sin nβ
∴ xm yn = (cos mα + i sin mα)(cos nβ + i sin nβ)
= cos (mα + nβ) + i sin (mα + nβ) ——— (1)
\(\frac{1}{x^{m} \cdot y^{n}}\) = cos (mα + nβ) – i sin (mα + nβ) —— (2)
By adding (1) and (2).
xmyn + \(\frac{1}{x^{m} y^{n}}\) = 2 cos (mα + nβ)
By subtracting (2) from (1)
xmyn – \(\frac{1}{x^{m} y^{n}}\) = 2 sin (mα + nβ)
Question 14.
If n is a positive integer, show that (1 + i)n + (1 – i)n = 2\(\frac{n+2}{2}\) cos \(\left(\frac{n \pi}{4}\right)\) (A.P.) (Mar. ‘15)
Solution:
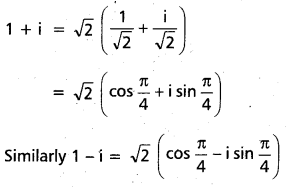

Question 15.
If n is an integer then show that (1 + cos θ + i sin θ)n + (1 + cos θ – i sin θ)n = 2n + 1 + cosn (θ/2) cos \(\left(\frac{\mathrm{n} \theta}{2}\right)\). (May ’11)
Solution:
L.H.S.

![]()
Question 16.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ, Prove that cos2 α + cos2 β + cos2 γ = \(\frac{3}{2}\) = sin2 α +
sin2 β + sin2 γ. (A.P. Mar. ‘16, T.S. Mar. ‘15, ’13)
Solution:
Let x = cos α + i sin α
y = cos β + i sin β
z = cos γ + i sin γ
∴ x + y + z = (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 + i.0 = 0
(x + y + z)2 = 0
⇒ x2 + y2 + z2 + 2(xy + yz + zx) = 0
x2 + y2 + z2 = -2(xy + yz + zx)
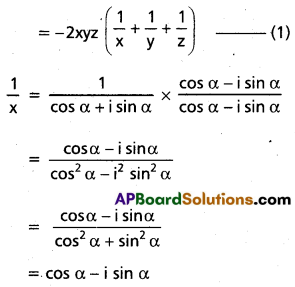
Similarly \(\frac{1}{y}\) = cos β – i sin β
\(\frac{1}{z}\) = cos γ – i sin γ
∴ \(\frac{1}{x}\) + \(\frac{1}{y}\) + \(\frac{1}{z}\) = (cos α + cos β + cos γ) – i(sin α + sin β + sin γ) = 0 – i. 0 = 0
Substituting in (1)
x2 + y2 + z2 = 0
(cos α + i sin β)2 + (cos β + i sin β)2 + (cos γ + i sin γ)2 = o
(cos 2α + i sin 2α) + (cos 2β + i sin 2β) + (cos 2γ + i sin 2γ) = 0
(cos 2α + cos 2β + cos 2γ) + i (sin 2α + sin 2β + sin 2γ) = 0
Equating real parts
cos 2α + cos 2β + cos 2γ = 0
2 cos2α – 1 + 2 cos2β – 1 + 2 cos2γ – 1 = 0
2 (cos2α + cos2β + cos2γ) = 3
cos2α + cos2β + cos2γ = \(\frac{3}{2}\)
∵ cos2α + cos2β + cos2γ = \(\frac{3}{2}\)
⇒ (1 – sin2α) + (1 – sin2β) + (1 – sin2γ) = \(\frac{3}{2}\)
⇒ sin2α + sin2β + sin2γ = 3 – \(\frac{3}{2}\) = \(\frac{3}{2}\)
∴ cos2 α + cos2β + cos2γ = \(\frac{3}{2}\)
= sin2 α + sin2β + sin2β
Question 17.
Find all the values of (\(\sqrt{3}\) + i)1/4.
Solution:

Question 18.
Find all the roots of the equation
x11 – x7 + x4 – 1 = 0.
Solution:
x11 – x7 + x4 – 1 = 0
⇒ x7(x4 – 1) + 1 (x4 – 1) = 0
⇒ (x4 – 1) (x7 + 1) = 0
Case(i) : x4 – 1 = 0
x4 = 1 = (cos o + i sin 0)
⇒ x4 = (cos 2kπ + i sin 2kπ)
∴ x = (cos 2kπ + i sin 2kπ)1/4
⇒ x = cis \(\left(\frac{2 k \pi}{4}\right)\) = cis \(\frac{\mathrm{k} \pi}{2}\), k = 0, 1, 2, 3.
Case (ii): x7 + 1 = 0
⇒ x7 = -1 = cos π + i sin π
⇒ x7 = cos (2kπ + n) + i sin (2kπ + π)
∴ x = [cos (2k + 1)π + i sin (2k + 1)π]1/7
⇒ x = cis(2k + 1)\(\frac{\pi}{7}\), k = 0, 1, 2, 3, 4, 5, 6
The values of x are
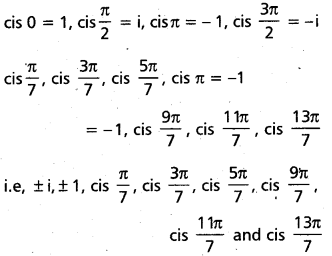
![]()
Question 19.
If 1, ω, ω2 are the cube roots of unity prove that (TS. Mar. ‘16)
i) (1 – ω + (ω2)6 + (1 – ω2 + ω)6 = 128
= (1 – ω + ω2)7 + (1 + ω – ω2)7
ii) (a + b)(aω + bω2)(aω2 + bω) = a3 + b3
iii) x2 + 4x + 7 = 0 where x = ω – ω2 – 2.
Solution:
∵ 1, ω, ω2 are the cube roots of unity
⇒ 1 + ω + ω2 = 0 and ω3 = 1
i) (1 – ω + ω2)6 + (1 – ω2 + ω)6
= (-ω – ω)6 +(-ω2 – ω2)6
= (-2ω)6 + (-2w2)6
= 26 (ω6 + ω12)
= 26(1 + 1) = 26 × 2 = 27 = 128 .
Again (1 – ω + ω2)7 + (1 + ω – ω2)7
= (1 + ω2 – ω)7 + (1 + ω – ω2)7
= (- ω – ω) + (-ω2 – ω2)7
= (-2ω)7 + (-2ω2)7
= (-2)7 (ω7 + ω14)
= (-2)7(ω + ω2)
= -(2)7 (-1)
= 27 = 128
ii) (a + b) (aω + bω2) (aω2 + bω)
= (a + b) [a2ω3 + abω4 + abω2 + b2ω3]
= (a + b) [a2 + ab(ω2 + ω4) + b2]
= (a + b) [a2 + ab(ω2 + ω) + b2]
= (a + b) (a2 – ab + b2) = a3 + b3
iii) x = ω – ω2 – 2
= x + 2 = ω – ω2
(x + 2)2 = ω2 – 2ω3
⇒ x2 +4x + 4 = ω2 + ω – 2
⇒ x2 + 4x + 4 = (-1) – 2 = -3.
⇒ x2 + 4x + 7 = 0
Question 20.
If α, β are the roots of the equation x2 + x + 1 = 0 then prove that α4 + β4 + α-1β-1 = 0
Solution:
Since α, β are the complex cube roots of unity.
We take α = ω, β = ω2
∴ α4 + β4 + α-1 + β-1
= ω4 + (ω2)4 + \(\frac{1}{\omega} \cdot \frac{1}{\omega^{2}}\)
= ω + ω2 + \(\frac{1}{\omega^{3}}\)
= (-1) + \(\frac{1}{1}\)
= -1 + 1 = 0
∴ α4 + β4 + α-1 + β-1 = 0